导弹固体火箭发动机贮存寿命预测方法研究*

陈海建，石伟峰

(海军驻北京地区舰空导弹系统军事代表室，北京　100854)



综合保障性技术

导弹固体火箭发动机贮存寿命预测方法研究*

陈海建，石伟峰

(海军驻北京地区舰空导弹系统军事代表室，北京100854)

摘要：为更准确地预测导弹固体火箭发动机贮存寿命，提出将Monte Carlo随机有限元法与RBF神经网络相结合，对固体发动机贮存寿命进行预测。对固体火箭发动机的结构可靠性利用Monte Carlo随机有限元法开展了不确定性分析，以此获得药柱的结构可靠性指标；基于RBF神经网络对固体发动机可靠性下降趋势进行预测，进而预测出导弹固体发动机寿命。

关键词：固体火箭发动机；导弹；随机有限元;人工神经网络；贮存寿命；预测

0引言

从可靠性的角度来说，对导弹固体火箭发动机进行寿命预估即是预先估算发动机可靠性的变化规律，确定可靠性下限，进而确定其寿命。考虑到可更换性和造价，导弹固体火箭发动机寿命主要取决于药柱的寿命，而药柱的寿命与其结构可靠性和性能可靠性密切相关，其中又以结构可靠性为主要因素[1-2]。固体火箭发动机的结构可靠性分析针对参数、特征量的不确定性进行研究，可以得到发动机药柱的结构完整性的可靠性指标，并根据可靠性下降的趋势来预估发动机的可靠性寿命。

目前常用确定性方法[3-7]对药柱结构问题进行研究，但由于生产工艺、贮存环境、推进剂物理特性等不确定性因素影响，确定性方法在此具有一定的局限性。针对此问题，本文即以确定性有限元法为基础，结合MonteCarlo抽样技术，形成MonteCarlo随机有限元法。基于MonteCarlo随机有限元法对固体火箭发动机在点火过程中的应变进行统计分析，利用应力—强度干涉模型计算不同贮存期内的药柱点火瞬间的可靠度。神经网络能实现从输入到输出状态空间的高度非线性映射，利用此特点，基于RBF神经网络对随机有限元分析所得到的发动机药柱可靠度进行预测，以可靠度随时间的变化规律为依据，预测导弹固体发动机贮存寿命。

1基于MonteCarlo随机有限元法的药柱结构可靠性分析

随机有限元法是确定性有限元分析与随机分析方法的结合。对真实药柱进行结构分析一般需借助有限元法，考虑随机因素可以采用随机分析理论，两者结合就称为随机有限元法。随机有限元法的发展，为解决药柱不确定性问题的研究带来了希望。

1.1MonteCarlo随机有限元法

MonteCarlo随机有限元法是MonteCarlo抽样技术与有限元法相结合的产物，能够便捷地调用确定性有限元的计算程序。MonteCarlo随机有限元法自身适应性很强，模拟过程不需要把状态函数进行线性化和随机变量当量正态化处理，与极限状态函数的非线性程度没有任何关系，随机变量维数也不会影响收敛速度，能够直接求解失效概率，因此本文基于MonteCarlo随机有限元法对导弹固体火箭发动机药柱进行可靠性分析。主要有以下4个步骤：

步骤1：随机变量的确定和抽样。确定随机变量概率分布，并据此进行抽样。

步骤2：结构响应分析。采用三维粘弹有限元法，分别对前面的抽样进行分析和求解，得到药柱结构的响应(位移、应力、应变等)。

步骤3：响应量统计分析。把上一步得到的计算结果进行概率统计分析，分别得到响应量的均值、方差甚至概率分布函数等统计特征。

步骤4：计算可靠度。在所有得到的数据的基础上，用概率统计方法计算药柱结构的可靠度。

1.2应力—强度干涉模型

本文基于MonteCarlo随机有限元方法，引入应力—强度干涉模型评估发动机药柱可靠性。此处的应力是指广义的应力，包括推进剂、粘结界面的最大应力或最大应变；与之对应的广义强度可以是最大拉伸强度、最大延伸率等。

在药柱的功能函数中，假定强度I和应力S为基本随机变量，服从正态分布且相互独立，则功能函数可表示为

Z=g(I,S)=I-S，

(1)

结构可靠度的表达式为

R=P(Z>0)=P(I-S>0).

(2)

图1给出了同一图上所表示的应力S和强度I的概率密度曲线，相交区域如阴影部分所示，是结构可能出现的故障区域，称为干涉区。由图1可以看出，当药柱的强度和工作应力越接近，离散程度越大，干涉部分就可能增大，药柱的不可靠度也就加大；推进剂性能愈好，工作应力小且稳定，则它们的分布离散度将减少，干涉部分相应地减少，发动机药柱的可靠度也就愈高。只要干涉区存在，就表示药柱结构有失效的可能性，但阴影区面积并不表示失效概率。在应力S和强度I的概率密度曲线已知的情况下，可根据干涉模型进行可靠性的定量计算。

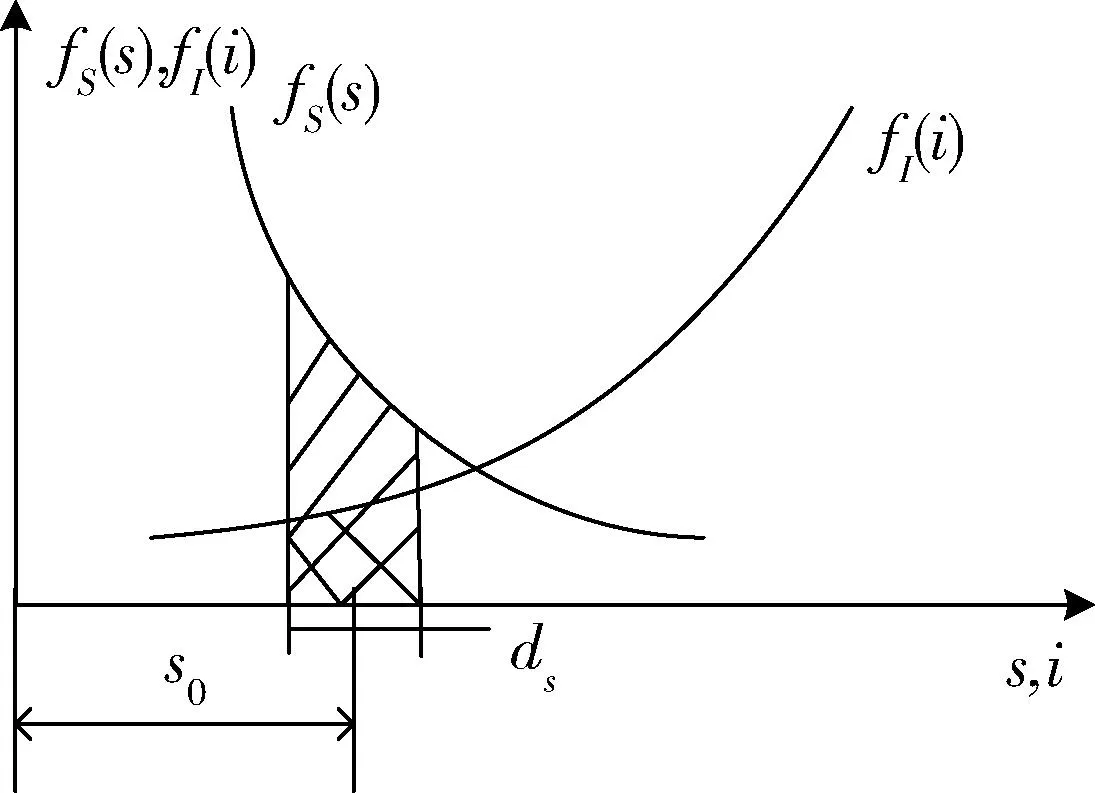
图1　应力—强度干涉图Fig.1　Model of stress-strength interference

图2为干涉区放大图。取某一应力定值s0，在此领域内， 取一小区间ds， 计算应力出现在此区间

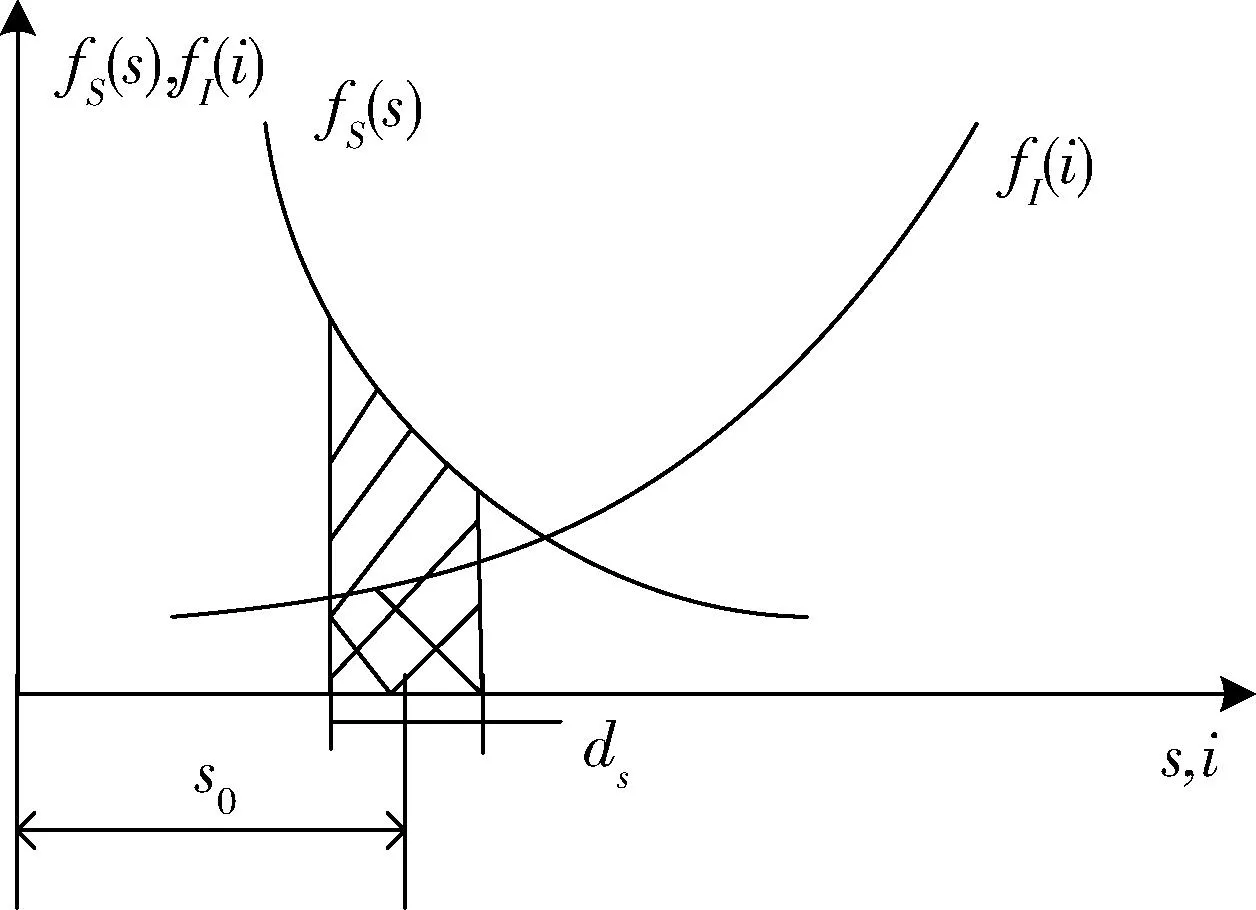
图2　干涉区Fig.2　Intervene area

内的概率为

(3)

强度I大于定值应力s0的概率为

(4)

由于应力和强度互相独立，故应力取值在s0领域和强度大于s0这2个事件同时发生的概率P为二事件单独发生概率的乘积，则

(5)

即可得到因干涉存在而引起的可靠概率。这一可靠概率表达式，对于任意s0的任意取值均应成立。即该结构的可靠度为

(6)

由于应力和强度服从正态分布，则应力S的概率密度函数为

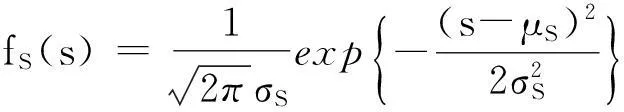
(7)

式中：σS为应力S的标准差;μS为应力S的均值。

强度I的概率密度函数为

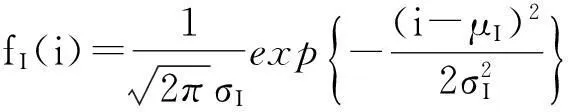
(8)

式中：σI为强度I的标准差；μI为强度I的均值。

功能函数Z亦服从正态分布，其均值和方差分别为

μZ=μI-μS，

(9)

(10)

结构可靠度的表达式为

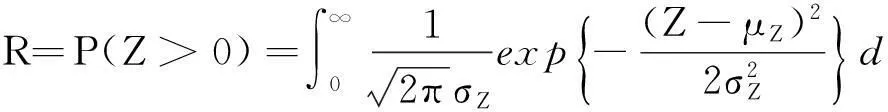
(11)

将随机变量Z化为标准正态分布的形式，即令x=(Z-μZ)/σZ。

当Z=0时，x的积分下限为

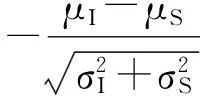
此时，式(11)变为

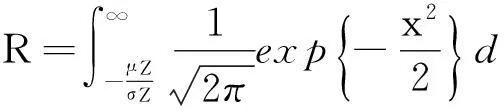
(12)

利用正态分布的对称性，式(12)也可表示为

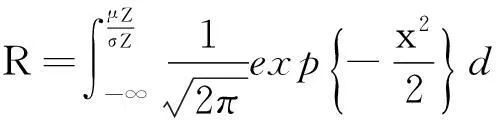
(13)

在结构可靠性问题中，通常令

(14)

式中：称β为可靠指标。则可靠度表达式(13)也可表示为

(15)

因此，在求得可靠指标β后，可由标准正态分布表查得可靠度R。

2基于RBF神经网络的药柱贮存寿命预测

目前常用参数模型法[8-12]进行贮存可靠性预测，此方法虽然简单易行，但往往要求有较多数据，具有一定的变化规律，而且对高度非线性问题不能很好的解决，有着一定的局限性。研究可知，神经网络具有从输入到输出状态空间高度非线性映射的特点，可克服参数模型法的局限性，更好地解决贮存可靠性预测的问题[13]。

20世纪80年代末，J.Moody和C.Darken研究提出径向基函数RBF网络，目前已广泛应用于数据预测，它能够以任意精度逼近任意连续函数。RBF网络由输入层、隐层、输出层构成。其网络拓扑结构如图3所示。

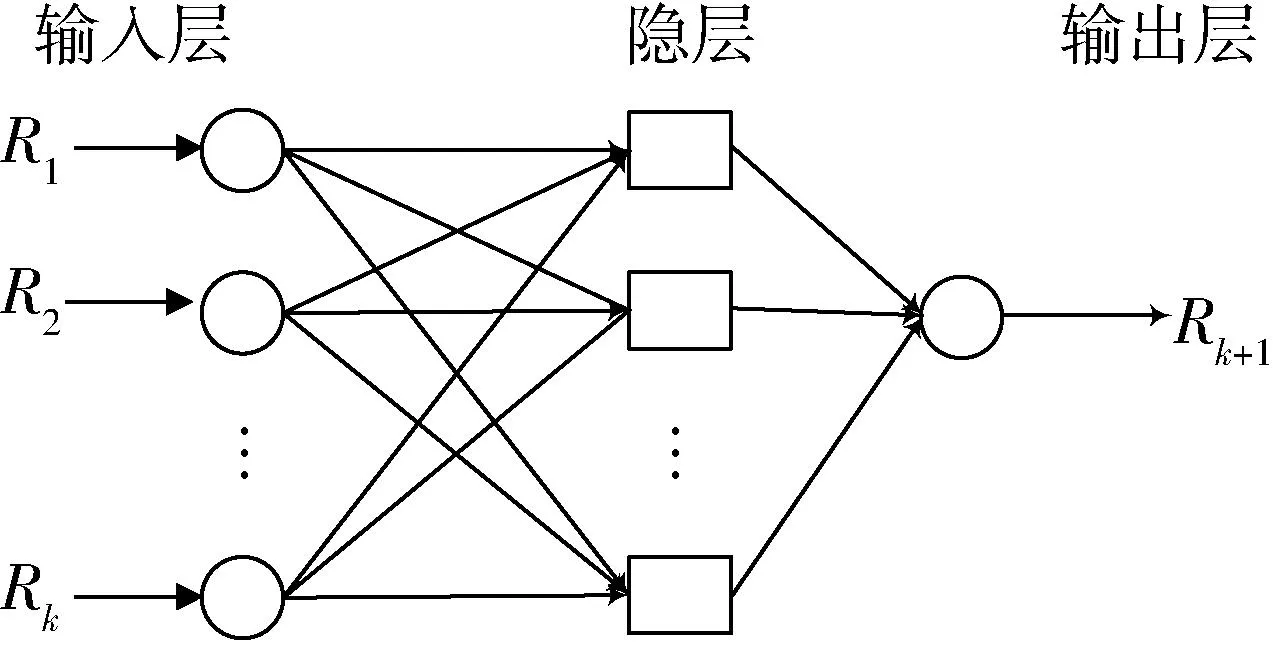
图3　RBF神经网络拓扑结构Fig.3　RBF net configuration

径向基函数采用高斯函数作为网络中输入层到隐层的传递函数

(16)

式中：μi为中心；x为输入维；σi为径向基函数的宽度。

中间层到输出层的传递函数采用线性函数

f(x)=x.

(17)

要实现RBF网络的预测功能，需要收集并对样本数据进行归一化处理、依据样本对RBF网络进行训练以满足要求。利用训练好的RBF网络，对药柱贮存可靠性变化趋势进行预测，设定药柱可靠性下限，即可获知导弹固体发动机贮存寿命。

3实例分析

以某型固体火箭发动机为例进行分析。

3.1基于MonteCarlo随机有限元法的药柱结构可靠度仿真

要对固体火箭发动机药柱进行MonteCarlo随机有限元分析，首先要确定所用推进剂力学性能参数和发动机载荷的准确的概率模型。在应力—强度干涉模型中，这里选取发动机点火期间推进剂最大应变作为“应力”，推进剂最大延伸率作为“强度”。为简化计算，在以最大应变为随机分析指标的情况下，可仅考虑推进剂模量、推进剂泊松比、内压载荷和温差载荷为随机参数，其他材料、载荷均做确定性参数处理。然而，目前要准确确定推进剂模量、推进剂泊松比、内压载荷和温差载荷的概率模型几乎是不可能的。经验证，这里对某型固体发动机药柱的推进剂模量、推进剂泊松比、内压载荷和温差载荷均采用正态分布描述。

图4给出了确定性有限元分析得到的某型固体火箭发动机药柱点火过程中的应变分布。

图4　药柱点火过程应变分布云图Fig.4　Strain of launching process

由图4可知，前、后翼槽为危险区域。本文在进一步的随机有限元分析中，重点以该区域为研究对象。随机参数值如表1所示。

表1　有限元分析随机参数表

应用MonteCarlo随机有限元法计算不同贮存期发动机点火期间最大应变的样本分布。以贮存5年的发动机为例，仿真得到的最大应变概率分布如图5所示。

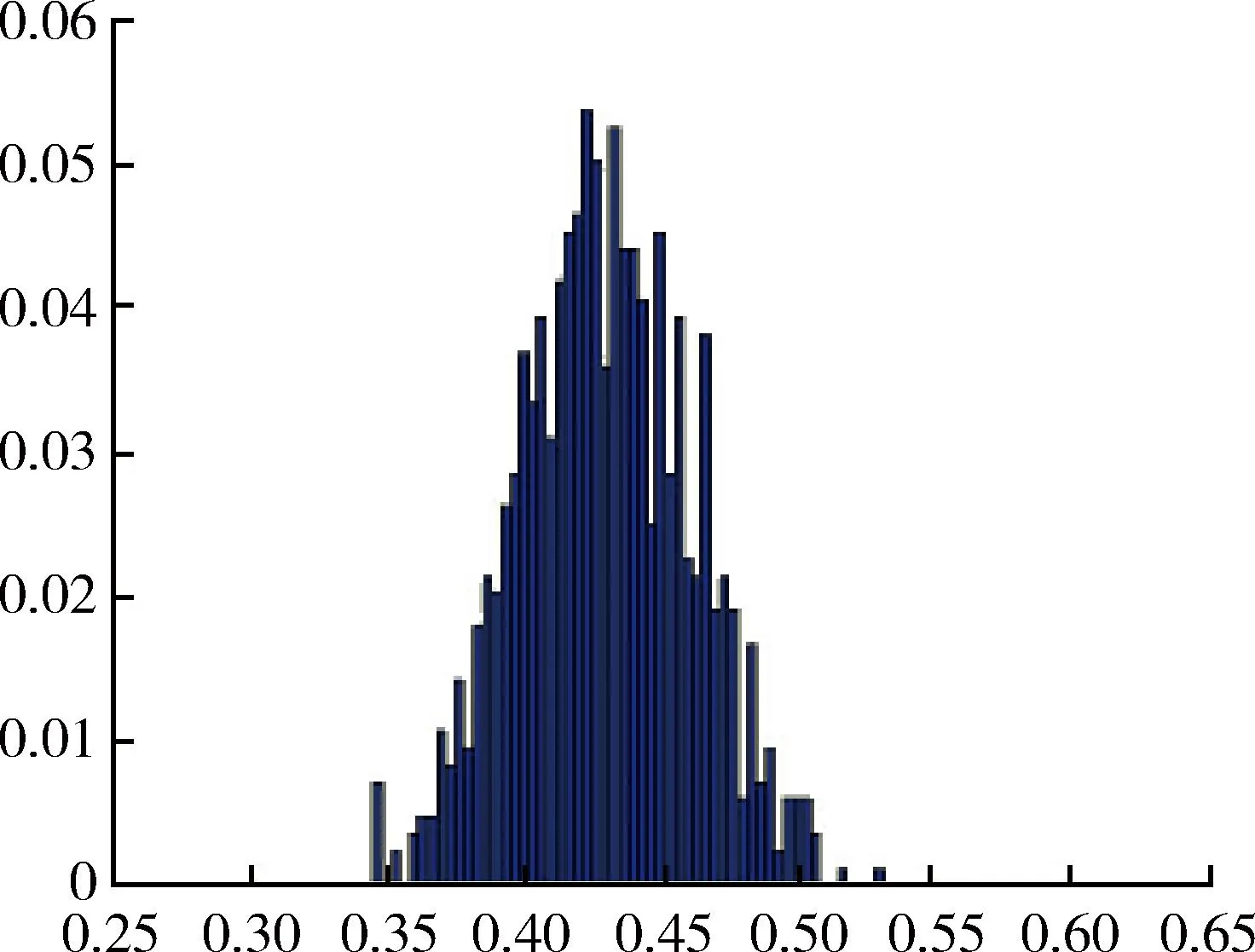
图5　药柱最大应变概率分布图Fig.5　Max stress probability distributionmap of grain

仿真得到的最大应变均值μεs=0.437 5，标准差σεs=0.022 7。根据文献[14]介绍的方法和文献[15]中的老化数据可进行计算，贮存5年的推进剂最大延伸率均值计算可得μεm=0.503 8，标准差σεm=0.021 5。则可靠度服从正态分布

0.983 0.

同理，可计算出某型固体火箭发动机药柱前五年的各时间节点的可靠度(以一个季度作为一个时间节点)，如表2所示。

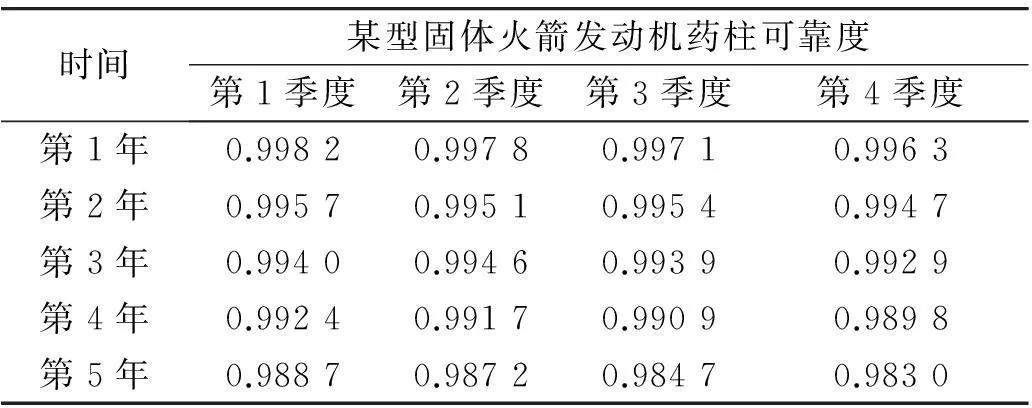
表2　固体火箭发动机药柱可靠度数据

3.2基于神经网络的固体发动机贮存寿命预测

借助神经网络算法进行预测，网络输入为连续的8个时间节点的数据，输出为下一时间节点的数据，分别应用BP和RBF网络来预测后续节点可靠度，样本数据如表3所示，前8组作为训练样本，对网络进行训练；后4组作为测试样本，通过预测值与原始值对比进行误差分析。

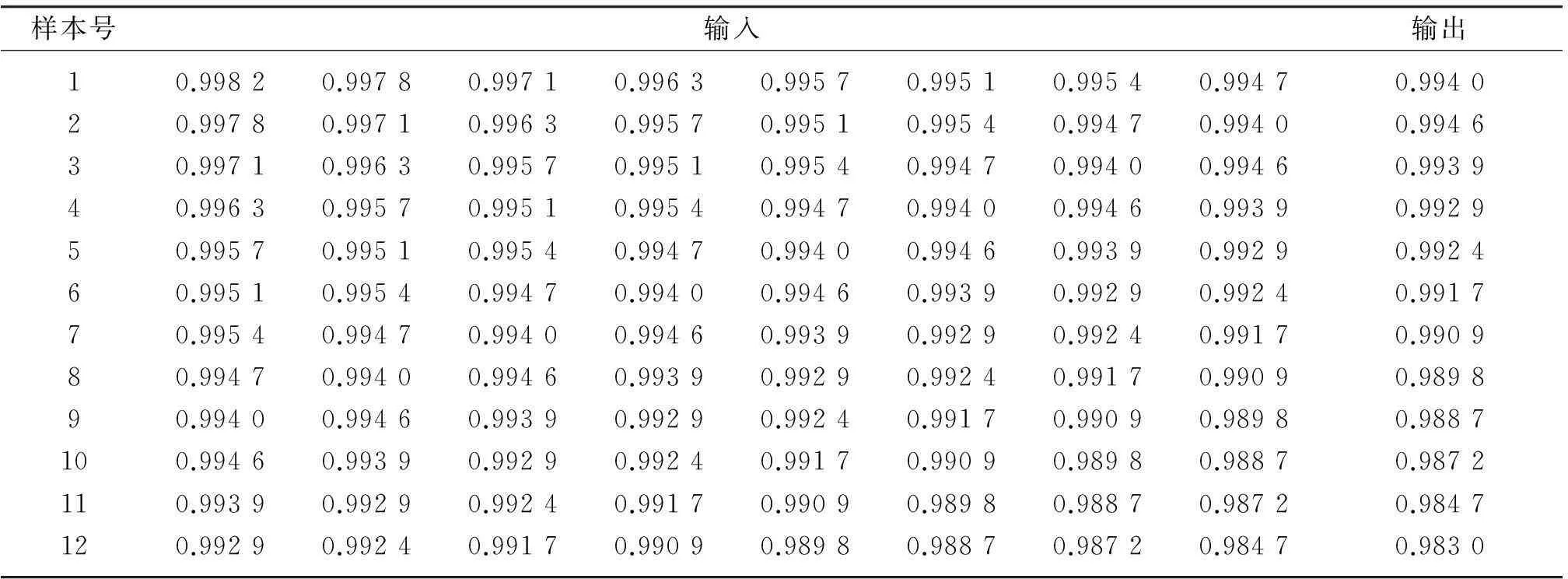
表3　训练样本与测试样本

利用Matlab工具对归一化后的样本数据进行网络训练。首先利用RBF网络进行参数的训练试运算，在此基础上预测发动机贮存可靠度。径向基函数分布密度SPREAD对RBF网络训练预测误差影响较大，从而影响预测结果。经本文试运算可以发现，当SPREAD为2时，网络预测误差相对来说最小，因此设定本文网络径向基函数分布密度SPREAD为2。

由表4可见基于RBF网络的某型固体火箭发动机可靠度的预测结果。基于RBF网络的贮存可靠度变化曲线及预估值见图6。

假定可靠度小于0.9时固体发动机贮存寿命到期。由表4及图6可知，点A(44.1,0.90)即为临界点，故可知其贮存寿命约为11年。通过以上算例的分析可以得出以下结论：

随机有限元分析与神经网络组合方法适用于固体发动机贮存寿命预测研究，并且相对于单一预测方法误差要小，能满足总体任务书所提出的某型发动机贮存寿命大于10年的要求，效果令人满意。

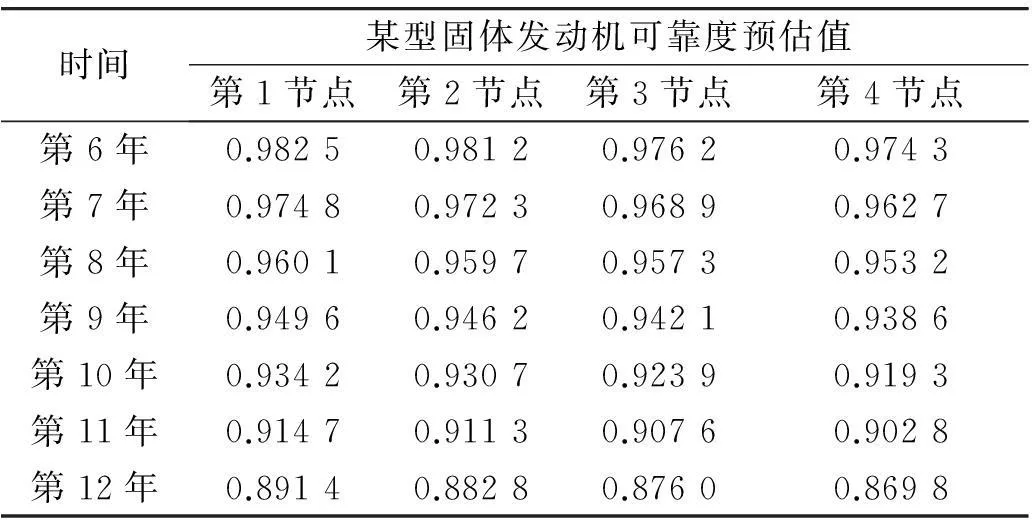
表4　基于RBF网络的某型固体发动机可靠度预估值

图6　基于RBF网络的贮存可靠度变化曲线及预估值Fig.6　Storage reliability mutative curve and forecast values based on RBF net work

5结束语

本文研究的基于随机有限元与神经网络组合模型的导弹固体火箭发动机贮存寿命预估方法，可实现对固体火箭发动机贮存寿命的较为精确的预测。克服了药柱结构不确定性问题和传统预测方法的局限性对精确预测贮存寿命带来的困难。本文的研究表明，MonteCarlo随机有限元法可以有效降低药柱结构不确定性问题对预测精度的影响；RBF神经网络能够实现高度非线性映射，克服了传统预测方法的局限性。通过本文的尝试，证明该方法可用于实现导弹固体火箭发动机贮存寿命的精确预测。

参考文献：

[1]田四朋. 固体火箭发动机药柱三维粘弹性响应面随机有限元分析[J]. 固体火箭技术，2010，33(1)：19-21.

TIANSi-peng.Three-DimensinalViscoelasticResponseSuifaceStochasticFiniteElementAnalysisonSolidRocketMotorGrain[J].JournalofSolidRocketTechnology, 2010，33(1)：19-21.

[2]PHILPOTTA,FRIDLEYKJ,ROSOWSKYDV.StructuralReliabilityAnalysisMethodforViscoelasticMembers[J].ComPut.Struct., 1994, 53(3): 591-599.

[3]邢耀国，杨欣毅，董可海，等. 固体火箭发动机装药失效判定研究的发展和展望[J]. 固体火箭技术，2004，27(7)：126-129.

XINGYao-guo,YANGXin-yi,DONGKe-hai,etal.ProgressandProspectoftheResearchonFailureforPropellantGrainswithDefectsinSRM[J].JournalofSolidRocketTechnology, 2004,27(7):126-129.

[4]王斌，常新龙. 固体火箭推进剂贮存使用寿命的累积损伤反应论模型[J]. 弹箭与制导学报，2007,27(1)：171-175.

WANGBin,CHANGXin-long.TheCumulativeDamage-ReactionTheoryLifeModeltotheStorageandUsageofSolidRocketPropellant[J].JournalofProjectiles,Rockets,MissilesandGuidance, 2007,27(1)：171-175.

[5]WHILTEJI.FiniteElementsinLinearViscoelasticity[C]∥InProceedings2ndConferenceMatrixMethodsinStructuralMechanics,AFFDL-TR-68-150,1968.

[6]ZIENKIEWICZOC,WASTONM,KINGIP.AMumericalMethodofVisco-ElasticStressAnalysis[J].InternationalJournalofMechanicsScience,1968,10(10):807-827.

[7]STRINATHAHR,LEWISRW.AFiniteElementMethodforThermoviscoelasticAnalysisofPlaneProblems[J].ComputerMethodsinAppliedMechanicsandEngineering, 1981, 25(1): 21-23.

[8]吴进煌，戴邵武，徐胜红. 基于可靠度预测模型的导弹贮存寿命分析方法[J]. 海军航空工程学院学报，2005，20(4)：477-479.

WUJin-huang,DAIShao-wu,XUSheng-hong.AnalysisMethodofMissileStorageLifeBasedonForecastingModelofStorageReliability[J].JournalofNavalAeronauticalandAstronauticalUniversity, 2005，20(4)：477-479.

[9]徐廷学. 基于定期检测的导弹贮存可靠性研究[J]. 弹箭与制导学报，2008，28(1)：248-250.

XUTing-xue.StudyonStorageReliabilityBasedonPeriodicalTestforMissiles[J].JournalofProjectiles,Rockets,MissilesandGuidance, 2008，28(1)：248-250.

[10]吴进煌，徐德民，宋贵宝，等. 战术导弹储存可靠性计算方法研究[J]. 西北工业大学学报，2008，26(3)：288-291.

WUJin-huang,XUDe-min,SONGGui-bao,etal.AStorageReliabilityCalculationMethodforaCertainMissile[J].JournalofNorthwesternPolytechnicalUniversity, 2008，26(3)：288-291.

[11]陈海建，滕克难，李波.基于模糊理论的导弹系统贮存可靠性仿真方法研究[J]. 弹箭与制导学报，2011，31(2)：33-35.

CHENHai-jian,TENGKe-nan,LIBo.TheResearchofMissileSystemStorageReliabilitySimulationMethodBasedonFuzzyTheory[J].JournalofProjectiles,Rockets,MissilesandGuidance, 2011，31(2)：33-35.

[12]庞建华，刘纪涛，张为华，等. 高能固体推进剂贮存寿命可靠性评估[J]. 弹箭与制导学报，2008,28(3)：169-172.

PANGJian-hua,LIUJi-tao,ZHANGWei-hua,etal.ReliabilityEvaluationofHigh-EnergySolidPropellantStorageLife[J].JournalofProjectiles,Rockets,MissilesandGuidance,2008,28(3)：169-172.

[13]陈海建，滕克难，李波，等.神经网络在导弹贮存可靠性预测中的应用[J]. 弹箭与制导学报，2010，30(6)：78-80.

CHENHai-jian,TENGKe-nan,LIBo,etal.ApplicationofNeuralNetworkonMissileStorageReliabilityForecasting[J].JournalofProjectiles,Rockets,MissilesandGuidance, 2010，30(6)：78-80.

[14]袁端才，唐金国，李海阳，等. 基于加速老化与三维粘弹性有限元分析的固体导弹发动机寿命预估[J]. 兵工学报，2006,27(4)：685-689.

YUANDuan-cai,TAGNJin-guo,LIHai-yang,etal.Three-DimensinalViscoelasticAnalysisandAcceleratedAgingApproachtoPredicttheServiceLifeofSolidMissileMotor[J].ACTA, 2006,27(4)：685-689.

[15]陈海建，滕克难，李波，等. 基于修正Arrhenius方法的SRM药柱储存寿命预估[J]. 弹箭与制导学报，2011(4)：232-235.

CHENHai-jian,TENGKe-nan,LIBo,etal.AResearchofSolidRocketMotorGrainStorageLifeForecastBasedonModifiedArrheniusMethod[J].JournalofProjectiles,Rockets,MissilesandGuidance, 2011(4)：232-235.

Method of Predicting Storage Life of Missile SolidRocketMotor

CHEN Hai-jian, SHI Wei-feng

(Military Representatives Office of Navy in the Second Research Academy of CASIC, Beijing, 100854, China)

Abstract:In order to predict the storage life of solid rocket motor, Monte Carlo stochastic finite element method and RBF neural network are combined to predict the storage life. The reliability of solid rocket motor structure is analyzed with Monte Carlo stochastic finite element method to obtain the structure reliability indicators of the grain. Based on RBF neural network, the decrease tendency of the reliability of solid motor is predicted and then the life cycle of the motor is predicted.

Key words:solid rocket motor; missile; stochastic finite element; artificial neural network; storage life; predicting

*收稿日期：2016-01-04；修回日期：2016-03-31

基金项目：有

作者简介：陈海建(1983-)，男，山东菏泽人。工程师，博士，研究方向为导弹可靠性研究。

通信地址：100854北京市海淀区142信箱83分箱E-mail：haijunzhixing@163.com

doi:10.3969/j.issn.1009-086x.2016.03.024

中图分类号：TJ760；V435

文献标志码：A

文章编号：1009-086X(2016)-03-0148-06