交叉眼干扰分析及实施方法*

付孝龙，白渭雄,杨忠 ,高绍忠

(1.空军工程大学 防空反导学院，陕西 西安　710051; 2.中国人民解放军91697部队，山东 青岛　266405)



探测跟踪技术

交叉眼干扰分析及实施方法*

付孝龙1，白渭雄1,杨忠1,高绍忠2

(1.空军工程大学 防空反导学院，陕西 西安710051; 2.中国人民解放军91697部队，山东 青岛266405)

摘要：交叉眼干扰属于2点源相干干扰，传统分析要得到较好的角度欺骗效果，对2点源振幅比及相位差有苛刻的要求。对交叉眼干扰的干扰原理进行了详细的数学推导，并仿真分析了2路干扰信号不同的振幅比及相位差对振幅和差式单脉冲雷达角度跟踪误差的影响。运用交叉眼干扰容限的概念，在分析交叉眼干扰特点的基础上，得出了与传统分析方法不同的2点源振幅比，及相位差可以在一定范围内变化且欺骗角度能够满足要求的结论，并在此基础上对有效实施交叉眼干扰的技术方法进行了探讨。

关键词：雷达电子战；单脉冲雷达；角度欺骗；相干干扰；交叉眼干扰；容限分析

0引言

单脉冲雷达对不具备角度欺骗能力的自卫式干扰具有免疫能力，传统的噪声压制不能有效干扰单脉冲雷达，反而会将实施者暴露在单脉冲雷达“眼”前，给飞机和舰船的生存带来更大的威胁[1-3]。交叉眼干扰[4-6]是一种先进的针对单脉冲雷达实施角度欺骗的电子攻击技术，战斗机在执行任务时亟需这种欺骗能力在导弹制导末段实施自卫保护[7]。从国外相关文献报道知，研究人员已在实验室及干扰样机上成功验证了交叉眼干扰的可行性和有效性[8-10]。

本文从交叉眼干扰信号的传播过程入手，建立干扰信号模型，对交叉眼干扰振幅和差单脉冲雷达进行了数学推导和仿真分析，对干扰在不同振幅比及相位差条件下的效果进行了分析。首先建立交叉眼干扰数学模型，然后采用仿真的方法对交叉眼干扰的各个参数进行分析，找出它们对交叉眼干扰性能的影响，结合交叉眼干扰容限的概念，最后结合仿真分析及交叉眼干扰特点归纳了有效实施交叉眼干扰的技术方法。

1数学模型

图1 2个“○”表示被干扰单脉冲雷达上下放置的2个天线1和2，2个“×”表示交叉眼干扰设备分置的2干扰天线A和B，“□”表示交叉眼干扰产生的虚假目标。dr是单脉冲2天线的间距；dc是2干扰天线的间距(也称基线长度)；d0表示假目标与干扰天线中心的距离；θr是单脉冲天线瞄准轴相对于单脉冲天线中心和干扰天线中心连线的旋转角度(也称单脉冲天线旋转角)；θc是干扰天线法向相对于单脉冲天线中心和干扰天线中心连线的夹角(也称干扰天线旋转角)；θe是2干扰天线与单脉冲天线中心形成的张角的一半；r是单脉冲天线中心和干扰天线中心之间的距离。

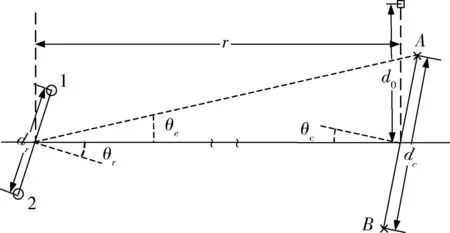
图1　交叉眼干扰场景Fig.1　Scenario of cross-eye jamming

由图1的几何关系可以得到:天线A和B相对于雷达瞄准轴的角度分别为θr+θe和θr-θe，雷达相对于交叉眼干扰天线A和B的角度分别为θc+θe和θc-θe。由于r≫dc，即θe值很小，对θe做如式(1)的近似：

(1)

设2单脉冲天线方向图为Fr1(θ)和Fr2(θ)，则其和、差方向图分别为

Fr∑(θ)=Fr1(θ)+Fr2(θ)，

(2)

FrΔ(θ)=Fr1(θ)-Fr2(θ).

(3)

交叉眼干扰设备天线的方向图为Fc(θ)，经过交叉眼干扰机后2路信号具有不同的增益和相移，这里假设由天线A到天线B的一路信号比另一路信号振幅增大了a倍，相位差为φ。

天线1和2接收到的信号都由2部分组成，一部分是天线A传播到天线B方向的信号；另一部分是由天线B传播到天线A方向的信号。雷达向天线A方向辐射的信号为

EA1(t,θ)=E(t)FrΣ(θr+θe).

(4)

信号被天线A接收，接收的信号为

EA2(t,θ)=E(t)FrΣ(θr+θe)Fc(θc+θe).

(5)

由天线A传播到天线B信号幅度增大了a倍，相位增加了φ，那么天线B辐射向天线1的信号为

EA3(t,θ)=E(t)FrΣ(θr+θe)Fc(θc+θe)aexp(jφ)·

Fc(θc-θe).

(6)

被天线1接收后的信号为

E1AB(t,θ)=E(t)FrΣ(θr+θe)Fc(θc+θe)aexp(jφ)·Fc(θc-θe)Fr1(θr-θe).

(7)

同理，由天线1接收的从天线B传播到天线A方向的信号为

E1BA(t,θ)=E(t)FrΣ(θr-θe)Fc(θc+θe)Fc(θc-θe)·

Fr1(θr+θe).

(8)

则天线1接收到信号为E1(t,θ)=E1AB(t,θ)+E1BA(t,θ)=E(t)Fc(θc+θe)·

Fc(θc-θe)[aexp(jφ)FrΣ(θr+θe)·

Fr1(θr-θe)+FrΣ(θr-θe)Fr1(θr+θe)].

(9)

天线2接收到的天线A传播到天线B方向的信号和由天线B传播到天线A方向的信号分别为E2AB(t,θ)=E(t)FrΣ(θr+θe)Fc(θc+θe)aexp(jφ)·

Fc(θc-θe)Fr2(θr-θe),

(10)

E2BA(t,θ)=E(t)FrΣ(θr-θe)Fc(θc+θe)Fc(θc-θe)·

Fr2(θr+θe).

(11)

则天线2接收到信号为E2(t,θ)=E2AB(t,θ)+E2BA(t,θ)=E(t)Fc(θc+θe)·

Fc(θc-θe)[aexp(jφ)FrΣ(θr+θe)·

Fr2(θr-θe)+Fr∑(θr-θe)Fr2(θr+θe)].

(12)

则和通道及差通道的信号分别为

EΣ(t,θ)=E1(t,θ)+E2(t,θ)=E(t)Fc(θc+θe)·

Fc(θc-θe)FrΣ(θr+θe)FrΣ(θr-θe)·

[aexp(jφ)+1]，

(13)

EΔ(t,θ)=E1(t,θ)-E2(t,θ)=E(t)Fc(θc+θe)·

Fc(θc-θe)[aexp(jφ)FrΣ(θr+θe)·

FrΔ(θr-θe)+FrΣ(θr-θe)FrΔ(θr+θe)],

(14)

经过混频，中放和AGC之后，鉴相器两端的输入信号为

uΣ(t,θ)=exp(jωmt)Fc(θc+θe)Fc(θc-θe)·

FrΣ(θr+θe)FrΣ(θr-θe)·

[aexp(jφ)+1],

(15)

uΔ(t,θ)=exp(jωmt)Fc(θc+θe)Fc(θc-θe)·

[aexp(jφ)FrΣ(θr+θe)FrΔ(θr-θe)+

FrΣ(θr-θe)FrΔ(θr+θe)].

(16)

经过鉴相器后，得到跟踪误差信号

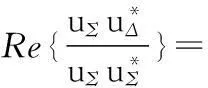
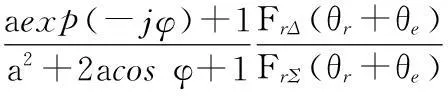
(17)

令S(θ)=0，那么θr的指向就是交叉眼干扰对雷达的欺骗角度，如果张角θe=0，那么式(17)可以化简，最终结果是单脉冲雷达对单目标的跟踪误差函数。

由式(15)和(16)可以看到交叉眼干扰天线增益Fc(θ)越大，接收信号的幅度就越大，而跟踪误差函数中并没有出现Fc(θ)，也就是说Fc(θ)不影响跟踪误差。因此可以得出一个结论：交叉眼干扰天线的方向图(增益)虽然影响雷达接收信号的幅度，但对跟踪误差却没有任何影响，文献[11-13]都得出了类似的结论。这在实际设计交叉眼干扰系统时非常重要，因为选择低增益，宽波束的天线就可以实现更大范围的有效干扰扇区，但干扰信号在与目标回波或者其它环境杂波竞争时需要发射机提供更大的功率；而高增益，窄波束的天线降低了系统对发射功率的需求，但同时有效干扰扇区也会变得很小。

在跟踪误差函数式(17)中可以看出跟踪误差和交叉眼支路振幅增益a，相位差φ，张角θe(或者距离r，基线dc)和单脉冲雷达天线的方向图有关。

2交叉眼干扰仿真分析

由于交叉眼干扰模型中函数式非常复杂，很多结论不能够通过数学表达式来清晰的表达，接下来将通过仿真的方法来分析交叉眼干扰的性能。

2.1交叉眼干扰对和通道信号的影响

根据式(13)可以得到和信号幅度和单脉冲雷达瞄准轴指向之间的关系曲线。图2所示的就是这样的曲线。图中不同曲线之间的振幅比a，相位差φ和张角θe对应着不同参数：曲线1：a=2，φ=151°，θe=0.186°；曲线2：a=3，φ=178°，θe=0.186°；曲线3：a=2，φ=160°，θe=0.186°；曲线4：a=2，φ=50°，θe=0.3°。

图2　交叉眼干扰对和通道信号幅度的影响Fig.2　Curves of amplitude of sum channel signal with cross-eye jamming

由图2知振幅比a，相位差φ和张角θe的变化虽然影响到和信号的幅度，但无论它们怎么变化和信号的最大值始终处于两干扰天线中心。这一结论说明交叉眼干扰对利用和通道定向的雷达(如圆锥扫描雷达)不具有干扰作用[11-12]，这一点也可以作为对抗交叉眼干扰的一种措施。

2.2振幅比对欺骗角度的影响

从跟踪误差曲线中提取出稳定跟踪点就能够得到欺骗角度，改变振幅比a来分析其对欺骗角度的影响。图3给出了振幅比a对欺骗角度影响的仿真结果，仿真中设置张角θe=0.5°，其他仿真参数见图3中。

图3　欺骗角度与振幅比的关系Fig.3　Deceiving angle varies with the relative amplitude

图3中在相位差φ靠近180°时，欺骗角度较大，随着振幅比a的增大先快速增加，然后缓慢减小；在相位差φ远离180°时欺骗角度较小且欺骗角度随着振幅比a的增大而增大，图3中的“■”表示的点是能够达到的所有欺骗角度中的最大值，称它为最大欺骗角度，记为θjmax=max{欺骗角度}，图3中最大欺骗角度θjmax≈1.22°。

2.3相位差对欺骗角度的影响

从跟踪误差曲线中提取出稳定跟踪点就能够得到欺骗角度，改变相位差φ来分析其对欺骗角度的影响，图4给出了仿真结果，仿真中设置张角θe=0.186°，其他仿真参数见图4中。

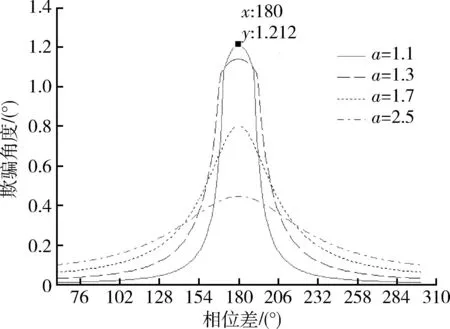
图4　欺骗角度与相位差的关系Fig.4　Deceiving angle varies with the phase shift

图4中无论a为何值，当相位差φ=180°时欺骗角度曲线均达到最大值，而当相位差φ远离180°时，欺骗角度随着减小，图4中“■”表示的点接近于最大欺骗角度。

2.4交叉眼干扰容限分析

振幅比a和相位差φ对欺骗角度的影响分析表明：即使振幅比a和相位差φ都在变化，只要在一定的范围内，交叉眼干扰都能够稳定的达到最大欺骗角度或者使跟踪误差曲线不存在稳定跟踪点，这个变化范围的大小可以通过交叉眼干扰的容限[13-16]来描述。交叉眼干扰的容限定义为：当振幅比a和相位差φ的值在一定的范围内变化，都能够保证交叉眼干扰引起的欺骗角度不小于某一值，这个范围就是交叉眼干扰的容限。当这个值为θn时交叉眼干扰的容限称为欺骗角度θn的容限，可见在这个容限内的欺骗角度都大于θn，而在边界上欺骗角度等于θn。

从图5中可以看到：交叉眼干扰振幅和差单脉冲雷达时只能在一个点上取到最大欺骗角度，即交叉眼容限是一个点，图中的“■”表示这个点，从它的坐标可以看出，当相位差φ=180°，振幅比a=1.005时，达到最大欺骗角度θjmax=1.251°。这个最大欺骗角度在实际中很难达到，因为它对相位差和振幅比的要求特别的严格，但从图5中可以看到，欺骗角度接近最大欺骗角度的容限还是很大的，例如图5中欺骗角度θn=1°的容限还是很大的，说明交叉眼干扰还是能够有效实现的。

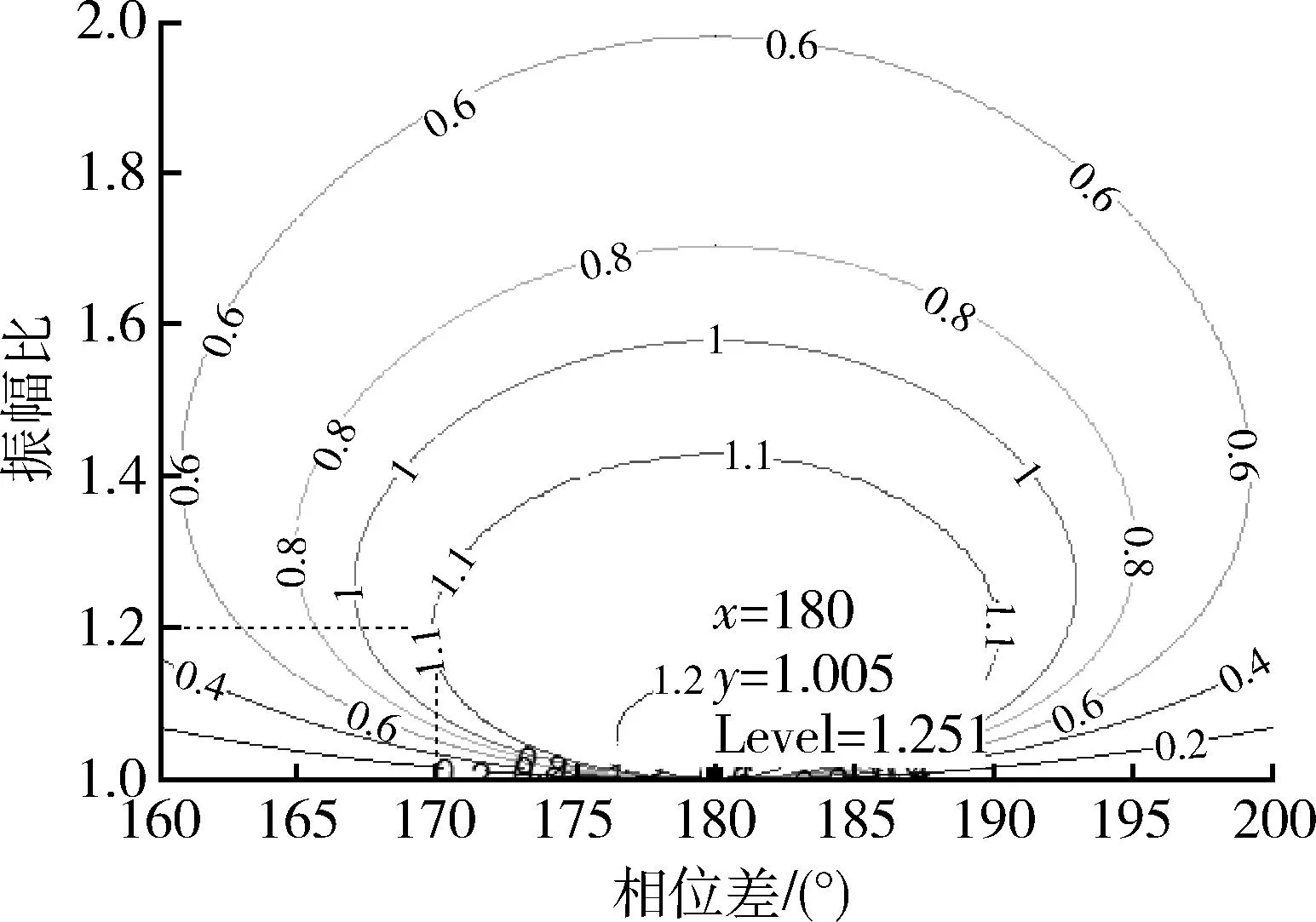
图5　欺骗角度的等高线图Fig.5　Contours of deceiving angle

3交叉眼干扰有效实施方法

如图6为无噪声、不同干扰条件下，交叉眼干扰角度随时间变化曲线，其中横轴时间用不同条件下达到最长欺骗干扰的时间进行了归一化处理，以方便比较各干扰条件下达到最大欺骗角度时的时间。各曲线参数为曲线1：a=1.1，φ=179°；曲线2：a=1.3，φ=170°；曲线3：a=1.7，φ=170°；曲线4：a=2.5，φ=179°。

图6　欺骗角度随时间变化曲线Fig.6　Contours of deceiving angle change over time

由图6知，振幅比a越小，2点源相位差越接近180°，被干扰天线接收到的合成干扰信号越小，使得目标回波信号对交叉眼干扰的影响不能忽略，因此交叉眼干扰达到稳定最大欺骗角度的时间越长。

如果交叉眼干扰在实施刚开始时就使欺骗角度保持在要求的状态，那么此时干扰信号功率会比较小，不能够很好的掩盖目标回波，捕获雷达的波门，因此在交叉眼干扰实施刚开始时应该让功率因素占优，这样可以容易掩盖目标捕获雷达的波门，然后才是稳定因素占优，有规律的将交叉眼干扰的状态调整到要求的状态。由于交叉眼干扰处理的威胁信号可能是多个信号，而且它们之间往往是不同频率的，所以进行移相操作时比较困难，需要一定的计算和调整时间，如果在使用时经常调整相位差，那么干扰的稳定性和有效性将无法保证，因此不易经常进行调整。从交叉眼干扰的分析中得出，相位差保持在180°时可以通过调整振幅比达到交叉眼干扰的任何状态，相位差保持在180°时其波动范围最大，而且调整信号的功率更加容易也更加迅速。

所以，交叉眼干扰在运用时的合理方法应该是一种功率“拖引”方法，首先是只使用一路天线转发高功率180°移相的干扰信号，此时高功率信号捕获雷达波门，然后按照一定的方式增大另一路信号的功率，并不对这一路信号做移相操作，直至将功率增加到交叉眼干扰所需要的状态，也就是欺骗角度θn的容限中心。如果同时配合距离和速度波门拖引，那么雷达将会被逼真的从真目标位置上诱骗到一个假目标的位置上，也可以通过这样的方式来释放多假目标干扰。

4结束语

本文对交叉眼干扰进行了全面而又细致的分析，通过数学推导得出在交叉眼干扰中干扰天线的方向图不影响干扰的欺骗效果，但对于干扰的有效实施具有重要作用。仿真分析了交叉眼干扰对单脉冲雷达和支路的影响及2点源不同振幅比及相位差对欺骗角度的影响，进行了交叉眼干扰容限分析，得出了一些新的结论。通过容限分析得出交叉眼有效实施干扰时，振幅比及相位差可以在一定范围内变化而保证欺骗角度不小于一定值，而不是以往分析中得出的对振幅比和相位差之间的匹配要求那么苛刻的结论。最后得出了交叉眼有效实施的一种“功率”拖引的方法。

参考文献：

[1]张永顺，童宁宁，赵国庆.雷达电子战原理[M].2版.北京:国防工业出版社,2010.

ZHANGYong-shun,TONGNing-ning,ZHAOGuo-qing.RadarElectronicWarfarePrinciple[M].2nded.Beijing:NationalDefenseIndustryPress,2010.

[2]NERIF.IntroductiontoElectronicDefenseSystem[M].Boston:ArtechHouse,1991.

[3]SamuelMSherman,DavidKBarton.单脉冲测向原理与技术[M].2版.北京:国防工业出版社,2013:6-13.

SamuelMSherman,DavidKBarton.MonopulsePrinciplesandTechniques[M]. 2nded.Beijing:NationalDefenseIndustryPress,2013:6-13.

[4]DuPlessisWP.PlatformSkinReturnandRetrodirectiveCross-EyeJamming[J].IEEETransactionsonAerospaceandElectronicSystems, 2012,48(1): 490-501.

[5]LIUSong-yang,DONGChun-xi,XUJin，etal.AnalysisofRotatingCross-EyeJamming[J].AntennasandWirelessPropagationLetters,IEEE, 2015,14: 939-942.

[6]ZOUJian-bin;GAOKai;LUShu-jun,etal.CoherentDecoysJammingAnti-RadiationMissiles[C]∥IEEEJordanConferenceonAppliedElectricalEngineeringandComputingTechnologies(AEECT), 2013: 1-5.

[7]NERIF.Anti-MonopulseJammingTechniques[C]∥Proceedingsofthe2001SBMO/IEEEMTT-SInternational.IEEE, 2001:45-50.

[8]FALKL.Cross-EyeJammingofMonopulseRadar[C]∥WaveformDiversityandDesignConference, 2007.International.IEEE, 2007:209-213.

[9]DuPlessisWP.PlatformSkinReturnandRetrodirectiveCross-EyeJamming[J].IEEETransactionsonAerospaceandElectronicSystems, 2012,48(1): 490-501.

[10]DuPlessisWP,OdendaalJW,JoubertJ.ExperimentalSimulationofRetrodirectiveCross-EyeJamming[J].IEEETransactionsonAerospaceandElectronicSystems, 2011,47(1): 734-740.

[11]SHANGZG,BAIWX,FUXL.AnalysisofCross-EyeJamming[C]∥InternationalProceedingsofComputerScience&InformationTech, 2012:104-109.

[12]YARONL,LANGERT,GEILERY,etal.Tur,M.Wideband0/πRetro-ReflectivePhotonicSystem[C]∥IEEEInternationalConferenceonMicrowaves,Communications,AntennasandElectronicsSystems(COMCAS), 2011: 1-4.

[13]马逸超.交叉眼干扰半实物仿真技术研究[J].现代防御技术，2014,42(1)：170-174.MAYi-chao.HardwareinLoopSimulationofCross-EyeJamming[J].ModernDefenceTechnology,2014,42(1):170-174.

[14]DuPlessisWP.AComprehensiveInvestgationofRetrodirectiveCross-EyeJamming[D].SouthAfrica:UniversityofPretoria,2010.

[15]DuPlessisWP,ODENDAALJW,JOUBERTJ.ExtendedAnalysisofRetrodirectiveCross-EyeJamming[J].Antennas&PropagationIEEETransactionson, 2009, 57(9):2803-2806.

[16]DuPlessisWP,ODENDAALJW,JOUBERTJ.ToleranceAnalysisofCross-EyeJammingSystems[J].IEEETransactionsonAerospaceandElectronicSystems, 2011,47(1): 740-745.

Analysis and Implementation of Cross-Eye Jamming

FU Xiao-long1，BAI Wei-xiong1，YANG Zhong1，GAO Shao-zhong2

(1.AFEU,Air and Missile Defence College, Shaanxi Xi’an 710051,China;2.PLA,No.91697Troop,ShandongQingdao266405,China)

Abstract:Cross-eye jamming is a coherent dual-source jamming. Conventional analysis has a strict restriction on relative amplitude and phase difference to induce an effective deceiving angle. A strict mathematical analysis about cross-eye jamming is presented and simulation analysis is carried out on amplitude-comparison monopulse radar with different relative amplitudes and phase difference of the two jamming sources. The results show that under certain conditions, a monopulse radar system can be deceived more easily by cross-eye jamming than suggested by conventional analysis based on the concept of cross-eye tolerance and the specialties of cross-eye jamming. The effective implementation of cross-eye jamming is achieved.

Key words:electronic warfare; monopulse radar; angle deception; coherent interference; cross-eye jamming; tolerance analysis

*收稿日期：2015-05-20；修回日期：2015-07-12

作者简介：付孝龙(1988-)，男，四川成都人。博士生，主要从事信息对抗理论与技术研究。

通信地址：710051西安市长乐东路甲字1号空军工程大学防空反导学院研2队E-mail：fuxiaolong_12@163.com

doi:10.3969/j.issn.1009-086x.2016.03.020

中图分类号：TN972+.1；TP391.9

文献标志码：A

文章编号：1009-086X(2016)-03-0121-06