机动性约束下的隐身低空突防航迹规划*

汪先超，汤子跃，朱振波，王海峰

(1. 空军预警学院，湖北 武汉　430019；2. 中国人民解放军93617部队，北京　101400)



导弹技术

机动性约束下的隐身低空突防航迹规划*

汪先超1,2，汤子跃1，朱振波1，王海峰2

(1. 空军预警学院，湖北 武汉430019；2. 中国人民解放军93617部队，北京101400)

摘要：机载预警雷达与地面预警雷达联合组网技术的迅速发展使得飞行器突防变得越来越困难。在考虑飞行器机动性约束的前提下提出了一种“隐身”低空突防航迹规划方法，该航迹规划一方面利用机载预警雷达的多普勒盲区实现相对于机载预警雷达的“隐身”，另一方面低空飞行可以有效规避地面预警雷达的探测，该航迹大大提高了飞行器突防的成功率。考虑到机载预警雷达的位置信息无法事先获取，给出了固定时间步长的搜索方法求解该规划模型。仿真实验结果证明了提出的机动性约束下的隐身低空突防航迹规划方法的正确性。

关键词：预警雷达；低空突防；机动性约束；航迹规划；多普勒盲区；多普勒速度门限

0引言

受地球曲率的限制，地面预警雷达不可避免地存在低空探测盲区，为了解决此问题，机载预警雷达应运而生，机载预警雷达具有很强的低空、超低空探测能力[1-4]。将二者联合组网使用，可以实现对全方位空间目标的无缝隙覆盖，使得飞行器突防[5-7]变得越来越困难。

机载预警雷达普遍采用脉冲多普勒(pulse Doppler, PD)体制，利用运动目标的多普勒效应，在频域中完成杂波背景下的目标检测[8-11]。但是由于载机平台的运动，引起了杂波多普勒谱的扩展，导致机载预警雷达存在不可忽略的多普勒盲区[12-13]。多普勒盲区是机载预警雷达的一个弊端，但是对于飞行器突防来说却是一个很好的利用点。

本文在考虑飞行器机动性约束的基础上，也就是在保证航迹可飞的前提下，提出了一种可“隐身”的低空突防航迹规划[14]方法。该航迹一方面利用机载预警雷达不可忽略的多普勒盲区实现相对于机载预警雷达的“隐身”；另一方面低空突防可以有效规避地面预警雷达的探测。因此，该突防航迹可以同时减少被机载预警雷达和地面预警雷达探测到的概率，大大增加了飞行器突防的成功率，具有一定的实际意义。

1机载预警雷达的多普勒盲区

在规划机动性约束下的隐身低空突防航迹之前，必须对机载预警雷达的多普勒盲区的形成机理进行一定的分析。

机载预警雷达普遍采用PD体制，利用运动目标的多普勒效应完成强杂波背景下的目标检测。然而，由于载机平台的运动使得杂波发生多普勒频移的同时，也会造成杂波多普勒谱的扩展，特别是由于主瓣杂波和高度线杂波扩展而形成的遮挡效应，将会对目标检测产生非常不利的影响。当目标的多普勒频率位于这两类杂波的遮挡区域时，将无法检测到目标信号，此时目标进入多普勒盲区。

目标相对于机载预警雷达的径向速度决定了其多普勒频率，继而决定了目标是否落入多普勒盲区。令va和vb分别为载机和目标的速度，φa和φb分别为载机和目标的速度方向与视距方向的夹角，则目标相对于载机的径向速度为

vR=vacosφa-vbcosφb，

(1)

此时，目标的多普勒频率为

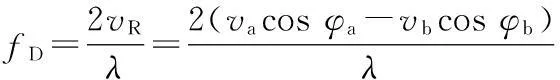
(2)

当目标的多普勒频率fD接近于0时，目标回波信号在频域上落入高度线杂波区。高度线杂波只分布在载机正下方的近距离处，然而目标和高度线杂波一般分布于不同的距离单元，因此可以较容易抑制高度线杂波。

主瓣杂波分布于多个距离单元，研究PD雷达的多普勒盲区其实主要就是研究主瓣杂波引起的多普勒盲区。主瓣杂波谱的中心处频率为

(3)

令主瓣杂波谱的展宽为Δf，当目标的多普勒频率fD∈[fa-Δf,fa+Δf]时，目标回波信号在频域上落入主杂波区，从而无法被检测。此时，目标落入多普勒盲区的条件为

(4)

由式(4)可知，目标落入多普勒盲区的条件也可以表示为

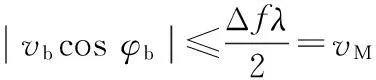
(5)

式中：vM表示机载预警雷达的多普勒速度门限，由主杂波宽度和波长所决定。具体PD雷达的多普勒速度门限是很难确定的，在实际工程应用中通常在30～50 m/s之间选择一个经验常数当作多普勒速度门限。

2机动性约束下的隐身低空突防航迹规划

考虑航迹规划模型的简单性，这里假设飞行器在固定的高度上低空突防。图1为飞行器与机载预警雷达的几何位置关系示意图。Oxy面为飞行器的低空突防平面，距离地面的高度为h，坐标原点O是突防任务的终点，飞行器与突防任务终点O的距离是R，φ表示飞行器的速度方向与视距方向的夹角。

“隐身”低空突防航线规划需要通过我方的探测设备实时掌握敌方机载预警雷达的位置，其位置坐标可以用时间t的函数表示，令机载预警雷达的位置坐标为(xa(t),ya(t),za(t))。

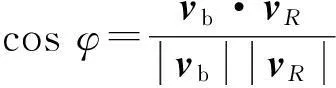
(6)

式中：·表示向量的内积运算。

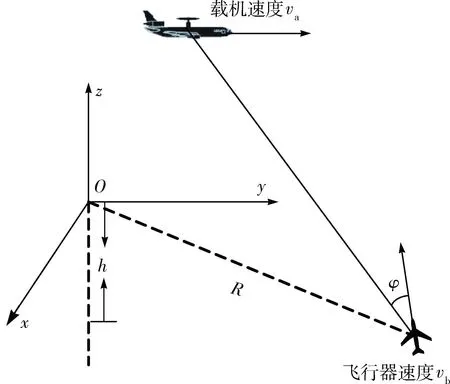
图1　机载预警雷达和飞行器几何位置关系图Fig.1　Geometrical relationship between AEW radar and aircraft

低空突防航迹的解析式可表示为p(t)=(x(t),y(t))，航迹的曲率半径为

(7)

曲率半径反映了航迹偏离直线的程度。

飞行器的运动受其机动性的约束，只有在满足机动性约束的空间内进行规划，才能保证所得轨迹的实际可飞性[15-16]。飞行器在水平面内的机动能力主要体现在最小转弯(曲率)半径上。令飞行器的最小转弯半径为rmin，本文提出的机动性约束下的隐身低空突防航迹规划建立如下：

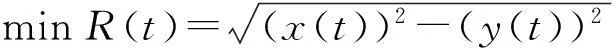
r(t)≥rmin,

vM≤vb≤vmax，

(8)

式中：R(t)表示t时刻飞行器与突防任务终点O的距离；vmax表示飞行器的最大突防速度。

突防航迹规划(8)中的目标函数是要飞行器在最短时间内突防；第1个约束函数是要飞行器一直处于多普勒盲区中，实现相对于机载预警雷达的“隐身”；第2个约束函数是利用最小转弯半径对规划的搜索空间进行一个合理的限制，保证航迹的实际可飞行。通过该规划求得飞行器在每个时刻的坐标，连接起来就可以得到本文所需要的低空突防航迹。

机载预警雷达的位置坐标是通过我方的探测设备实时获取的；飞行器的位置坐标需要通过航迹规划实时求得，且飞行器需迅速就位；这些决定了航迹规划(8)的最好求解方法是固定时间步长的搜索方法。假设搜索时间步长为t0，飞行器在x轴和y轴上的速度分量可近似表示为

(9)

利用固定时间步长的搜索方法求解航迹规划(8)的具体实现过程就是利用t-t0和t时刻飞行器的位置坐标以及t+t0时刻机载预警雷达的位置坐标，求t+t0时刻飞行器的位置坐标；然后再利用t和t+t0飞行器的位置坐标以及t+2t0时刻机载预警雷达的位置坐标，求得t+2t0时刻飞行器的位置坐标，如此反复，当飞行器接近突防任务终点O点，搜索终止。

每一步的搜索求解方法如图2所示，以t时刻飞行器的位置坐标为圆点，分别以t0vM+i(t0vmax-t0vM)/N(i=0,1,…,N)为半径得到N+1个圆；然后在每个圆上等间隔取M个点，在所有这些点中判断满足多普勒盲区条件限制和机动性约束条件限制的点，再在这些满足条件的点中取距离任务突防终点最近的那个点，就是飞行器在t+t0时刻的位置坐标。

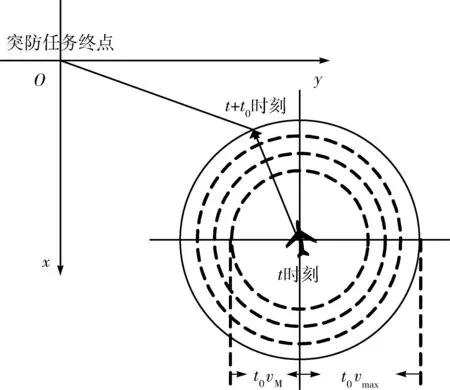
图2　搜索求解方法示意图Fig.2　Illustration for searching method

考虑到实际应用中飞行器的突防航迹不需要特别精确，搜索时间步长一般选择为1 s。如果敌方预警雷达的载机速度较快，时间步长要适当选择小一点，防止飞行器飞出机载预警雷达的多普勒盲区。

3仿真实验

利用Matlab编程工具对机动性约束下的隐身低空突防航迹规划进行仿真实验。仿真实验参数设置如下：假设敌方机载预警雷达的航线为类似于田径运动场跑道的双平行线形航线，位于突防任务终点O的正上方，距离地面的高度为h=9 000 m，上下是长度为L=80 km的平行线段，两侧是半径为r=15 km的半圆，载机以固定速度va=150 m/s在航线上飞行，机载预警雷达的起始位置坐标为(-15,0,9)km；我方飞行器的低空突防高度h=300 m，飞行器的最大突防速度vmax=300 m/s，飞行器的起始位置坐标为(300,300 ,0)km，飞行器的最小转弯半径rmin=2 km。

用固定时间步长的搜索方法对“隐身”低空突防航迹规划模型进行求解，固定时间步长为1 s，N=10，M=400，当飞行器距离突防任务终点O小于40 km时，搜索终止。

图3　多普勒速度门限为30 m/s时隐身低空突防航线图Fig.3　Stealthy low-altitude penetration path when Doppler speed threshold is 30 m/s

图4　图3第1个转弯处航迹放大图Fig.4　Magnified drawing of the first turn in Fig. 3

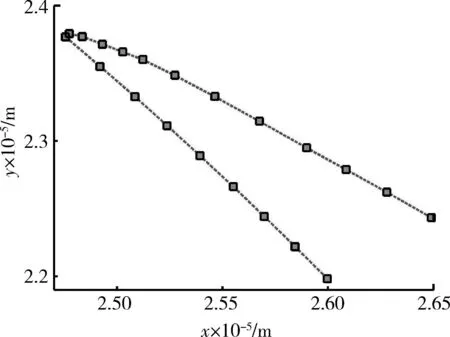
图5　图3第2个转弯处航迹放大图Fig.5　Magnified drawing of the second turn in Fig.3

图6　多普勒速度门限为40 m/s时隐身突防航迹图Fig.6　Stealthy low-altitude penetration path when　　Doppler speed threshold is 40 m/s

图7　图6第1个转弯处航迹放大图Fig.7　Magnified drawing of the first turn in Fig. 6

图8　图6第2个转弯处航迹放大图Fig.8　Magnified drawing of the second turn in Fig. 6

图3是多普勒速度门限vM=30 m/s时的隐身低空突防航迹图，航迹上每隔100 s显示一个点迹，突防所需时间为5 957 s。图4和图5分别是图3中第1个和第2个转弯处的放大图，图4是701～1 001 s的航迹图，每隔10 s显示一个点迹；图5是1 501～1 701 s的航迹图，每隔10 s显示一个点迹。图6是多普勒速度门限vM=40 m/s时的隐身低空突防航迹图，航迹上每隔100 s显示一个点迹，突防所需时间为4 827 s。图7和8分别是图6中第1个和第2个转弯处的放大图，图7是701～1 001 s的航迹图，每隔10 s显示一个点迹；图8是1 501～1 701 s的航迹图，每隔10 s显示一个点迹。

从仿真实验结果可以看出，机动性约束下的隐身低空突防航迹呈锯齿状，在转弯的地方，由于飞行器机动性的约束，航迹上有很长一段的低速调整期。此外，多普勒速度门限越大，锯齿形状越疏，锯齿的个数越少，成功突防所需要的时间也越短，这与强杂波背景下更有利于飞行器突防的常识是相吻合的。

表1是2种隐身低空突防方法进行突防所需时间的对比，第1种方法是飞行器以多普勒速度门限速度沿直线(飞行器突防起始位置和突防任务终点的连线)低空突防，这种突防方法的路径是最短的，且有“隐身”效果，但是突防所需时间很长，是本文提出的突防方法所需时间的2倍左右。本文提出的隐身低空突防方法所需时间少，且航迹具有变化性，增加敌方探测设备侦察的难度，可大大提高飞行器突防的成功率。

表1　两种隐身低空突防方法所需时间的对比

4结束语

本文在研究多普勒盲区形成机理的基础上，考虑到飞行器机动性的约束，提出了一种“隐身”低空突防航线规划方法。仿真实验结果显示：隐身低空突防航迹表现为锯齿状，多普勒速度门限越大，锯齿形状越稀疏，成功突防所需时间越少，这与强杂波地形条件下更有利于突防的常识是相吻合的。

本文提出的隐身低空突防方法所需时间少，是以多普勒速度门限速度低空突防方法所需时间的一半左右，且航迹具有变化性，增加了敌方探测设备探测的难度，可大大提高飞行器突防的成功率。对于战机、无人机和导弹等的“隐身”低空突防航迹规划具有一定的指导意义。

参考文献：

[1]陆军, 郦能敬, 曹晨. 预警机系统导论[M]. 北京: 国防工业出版社, 2011.

LU Jun, LI Neng-jing, CAO Chen. Introduction to Airborne Early Warning Systems[M]. Beijing: National Defence Industry Press, 2011.

[2]付莹, 汤子跃, 孙永健. 多预警机雷达信息融合的多普勒盲区目标检测[J]. 火力与指挥控制, 2013, 38(5): 772-776.

FU Ying, TANG Zi-yue, SUN Yong-jian. Blind Doppler Zone Target Detection Based on Muti-AEW Radar Information Fusion[J]. Fire Control & Command Control, 2013, 38(5): 772-776.

[3]粘松雷, 严建刚, 林云. 基于效能分析方法的预警机探测效能研究[J]. 现代防御技术, 2012, 40(4):38-41.

NIAN Song-lei, YAN Jian-gang, LIN Yun. EWA Detection Effectiveness Based on SEA Method[J]. Modern Defence Technology, 2012, 40(4): 38-41.

[4]李大鹏, 杨根源, 谭乐祖. 预警机支援下舰艇编队网络化协同反导研究[J]. 现代防御技术, 2013, 41(1): 9-14.

LI Da-peng, YANG Gen-yuan, TAN Le-zu. Warship Formation Network Centric Cooperative Antimissile Under Early Warning Aircraft Support[J]. Modern Defence Technology, 2013, 41(1): 9-14.

[5]何珮, 屈香菊, 武哲. 应用自适应遗传算法进行参考航迹规划[J]. 航空学报, 2003, 24(6): 499-502.

HE Pei, QU Xiang-ju, WU Zhe. Aircraft Referenced Flight Path Planning by Using Adaptive Genetic Algorithms[J]. Acta Aeronautica et Astronautica Sinica, 2003, 24(6): 499-502.

[6]姜玲玲, 陈怀民, 贾宝娟. 机动性约束下低空突防航迹规划算法研究[J]. 计算机仿真, 2011, 28(8): 80-82.

JIANG Ling-ling, CHEN Huai-min, JIA Bao-juan. Study on Low Altitude Penetration Path Planning Algorithm Under Flexibility Restraints[J]. Computer Simulation, 2011, 28(8): 80-82.

[7]LI Y, WU Z H, HUANG P L. A New Method for Analyzing Integrated Stealth Ability of Penetration Aircraft[J]. Chinese Journal of Aeronautics, 2010, 23(2): 187-193.

[8]GORDON N, RISTIC B. Tracking Airborne Targets Occasionally Hidden in the Blind Doppler[J]. Digital Signal Processing, 2002, 12(2): 383-393.

[9]DU S C, SHI Z G, ZANG W, et al. Using Interacting Multiple Model Particle Filter to Track Airborne Targets Hidden in Blind Doppler[J]. Journal of Zhejiang University Science A, 2007, 8(8): 1277-1282.

[10]CLARK J M C, KOUNTOURIOTIS P A, VINTER R B. A Methodology for Incorporating the Doppler Blind Zone in Target Tracking Algorithms[C]∥The 13th International Conference on Information Fusion Proceedings, 2010 (8): 1481-1488.

[11]LONG T, REN L X. PRF Pulse Doppler Stepped Frequency Radar[J]. Science in China (Series F), 2009, 52(5): 883-893.

[12]韩伟, 汤子跃, 朱振波. 多普勒盲区条件下的改进粒子滤波跟踪算法[J]. 宇航学报, 2013, 34(3): 417-425.

HAN Wei, TANG Zi-yue, ZHU Zhen-bo. An Improved Method for Tracking Targets in Doppler Blind Zone Based on Particle Filter[J]. Journal of Astronautics, 2013, 34(3): 417-425.

[13]韩伟, 朱振波, 汤子跃. 一种多普勒盲区条件下的多假设运动模型目标跟踪方法[J]. 电子与信息学报, 2013, 35(3): 516-523.

HAN Wei,ZHU Zhen-bo， TANG Zi-yue. A Method of Tracking Targets in Doppler Blind Zone Based on Multiple-Hypothesis Motion Models[J]. Journal of Electronics & Information Technology, 2013, 35(3): 516-523.

[14]WANG Y Y, WEI T T, QU X J. Study of Multi-Objective Fuzzy Optimization For Path Planning[J]. Chinese Journal of Aeronautics, 2012, 25(1), 51-56.

[15]SZCZERBA R J, PEGGY G, GLICKSTEIN I S. Robust Algorithm for Real-time Route Planning[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(3): 869-878.

[16]DONG Z N, ZHANG R L, CHEN Z J. Study on UAV Path Planning Approach Based on Fuzzy Virtual Force[J]. Chinese Journal of Aeronautics 2010, 23(3): 341-250.

Stealthy Low-Altitude Penetration Path Planning Under Flexibility Restraint

WANG Xian-chao1,2, TANG Zi-yue1, ZHU Zhen-bo1, WANG Hai-feng2

(1. Air Force Early Warning Academy, Hubei Wuhan 430019, China;2. PLA,No. 93617 Troop, Beijing 101400, China)

Abstract:With the rapid development of airborne early warning (AEW) radar and ground early warning radar combined networking technology, the penetration of aircraft becomes harder and harder. With the consideration of flexibility restraint, the model for the path planning of stealthy low-altitude penetration is established. The path planning is invisible relative to AEW radar using Doppler blind zone and low-altitude flight can avoid the detection of ground early warning radar. The route greatly increases the success rate of the aircraft’s penetration. Considering the position information of AEW radar cannot be obtained in advance, and a fixed-time-step searching method is adopted to solve the model. The simulation results demonstrate the correctness of the developed method for path planning of stealthy low-altitude penetration under flexibility restraint.

Key words:early warning radar; low altitude penetration; maneuverable confinement; path planning; Doppler blind zone; Doppler speed threshold

*收稿日期：2015-05-11；修回日期：2015-08-17

作者简介：汪先超(1980-)，男，安徽庐江人。助工，博士，主要研究方向为雷达信号与信息处理。

通信地址：430019湖北省武汉市江岸区黄浦大街E-mail：xc_wang@aliyun.com

doi:10.3969/j.issn.1009-086x.2016.03.003

中图分类号：TN95；V249

文献标志码：A

文章编号：1009-086X(2016)-03-0012-06