雷达组网探测效能评估*

崔玉娟，察豪

(海军工程大学 电子工程学院，湖北 武汉　430033)



雷达组网探测效能评估*

崔玉娟，察豪

(海军工程大学 电子工程学院，湖北 武汉430033)

摘要：根据构建原则建立分层次的雷达网探测效能评估体系，针对体系指标量化困难，评价模糊，结构多层次，运用模糊理论和层次分析法，结合控制区间和记忆模型对雷达组网探测效能评估。最后通过实例分析，证实了模糊层次分析控制区间和记忆模型方法的有效性和可操作性，为雷达组网优化部署奠下基础。

关键词：雷达组网；探测效能；模糊理论；层次分析法；控制区间和记忆模型；优化部署

0引言

现代战场环境的日趋复杂多变性促进了雷达应用研究的不断深入，面对传统电子干扰、反辐射导弹、隐身目标及空袭目标低空/超低空突防的四大威胁，雷达组网是一种高效且切实可行的方案。它不仅使雷达系统具有较强探测跟踪能力和战术性能，如全频段、多体制、多重叠系数等，而且也使其成为一个具有全方位、立体化、多层次的新型战斗体系，因此，成为各国军事研究人员的研究热点。其中一个热点问题就是如何评估组网后的雷达总体探测效能，这是雷达组网优化部署的前提和依据，针对该问题，文献[1-6]分别采用了层次分析法、模糊数学方法、灰色理论等方法进行了评估。但是雷达组网探测效能属于多目标决策问题，如果单纯利用上述方法的一种则造成部分信息丢失或者难以具体体现某些指标，定义上存在模糊交叉性。

借鉴上述文献的评估思路，本文将雷达组网探测效能评估看成是受多因素影响的风险评价，采用风险分析法对其进行评估。风险分析法常采用模糊数学[7-8]、Monte Carlo模拟[9]、控制区间和记忆模型(controlled intervals and memory ,CIM)[10-11]。但是采用CIM风险分析法对雷达组网探测效能评估也有其局限性，指标量化比较困难。为此，本文结合层次分析法和模糊理论建立起一种模糊层次分析CIM模型，即FACIM (fuzzy analytic controlled intervals and memory)模型，具体方法如下：首先综合分析评估对象，将其按照一定原则分为几个大层面；然后针对每一个大层面将其细化为小层面指标，从而建立起评估指标体系；最后，充分考虑实际约束条件，选用合适的风险评估方案来评估每一个细化的小层面指标，继而得到每一个大层面的指标和体系的总体探测效能的评估。从而实现对雷达组网探测效能的定量评估，为后续的雷达组网优化部署提供更为客观、准确的选择依据。

1建立雷达网探测效能体系

目前对于雷达探测效能定义，国内外并没有统一的定义标准。根据大量资料研究和专家探讨，在科学、合理、全面、简明原则下，结合国内外关于雷达组网研究的状况以及考虑实际环境对雷达组网探测效能的影响，运用层次分析法将雷达组网探测效能分成探测能力、目标容量、实时性、分辨力、情报处理能力、精确度等六大方面(主因素层)，并对上述六大方面进行具体细化成24个小方面指标(子因素层)，如表1所示。

2CIM模型介绍

CIM模型可称为概率分布的叠加模型，它的两个“替代”使得概率分布的叠加计算更简化和普通化，即相同宽度区间的直方图替代变量的概率分布，和替代概率函数的积分。该模型的概率分布特征清晰简单直观，对于因素比较繁杂的评价对象非常有效。在这里仅仅介绍应用比较多的并联响应模型。

并联响应模型具有较强实用性，它的原理可以理解为物理电学中的并联电路连接方式。为了便于分析和理解，简单地描述如下：例如在一项重大活动,影响其实现的因素有很多，每一项因素的好坏也决定活动实现的好与坏。文献[11]给出活动各个指标所组成概率组合，即并联模型。对于其计算，首先运用乘法运算计算出2个指标因子的概率组合，接着将其结果和第3个指标做乘法运算，以此类推，其概率表达式为

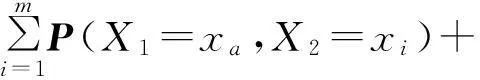
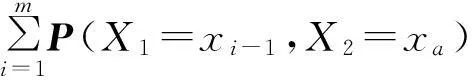
a=1,2,…,m，

(1)

式中：X1,X2为2个风险因素；xa为概率区间的组中值；m为分组数。

最后需注意的是上述并联响应模型讨论的前提是各个指标或影响因素相互独立。

3FACIM评估模型

从表1给出的各个指标可以看出，指标具有随机性、模糊性，一般很难量化它们，因此选用层次分析法，通过引入比例判断矩阵来确定评估指标因素的权重值，利用模糊法确定最末层指标因素的概率分布，最后利用CIM模型计算概率分布。

表1　雷达组网探测效能评估指标体系

3.1建立探测效能指标集

雷达组网探测效能的评价指标集用B=(B1,B2,B3,B4,B5,B6)表示，其中每个探测指标子集包括ni个探测指标，即Bs=(cs1,cs2,…,csni),s=1,2,…,6。它们满足条件：

(1)n1+n2+…+n6=n；

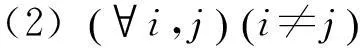
ni表示第i个探测指标子集的指标个数；n表示全部探测子集的指标个数。

3.2比例判断矩阵的AHP确定指标权重

在雷达组网探测效能评估中，指标权重值直接影响评价的结果。最常运用层次分析法来确定雷达组网探测效能评估指标的权重[12-14]，但是层次分析法中关键步骤是对判断矩阵一致性检验，往往构造出的判断矩阵不具有令人满意的一致性。引入比例系数矩阵，该矩阵不仅满足所需的一致性检验，而且容易得到矩阵的最大特征值以及其对应的特征向量，具体可以参见文献[15]。

3.3建立探测效能评价集

将探测效能评价集设为V={v1,v2,v3,v4,v5},v1,v2,v3,v4,v5分别表示指标的评价为“90～100分”、“80～89分”、“70～79分”、“60～69分”、“60分以下”，对应的探测风险程度分别为“低”、“较低”、“中等”、“一般”、“较高”。

3.4建立探测效能评价集

组织N名专家根据制定探测效能评价等级类别进行二级评价指标打分(百分制)归类，按式(2)计算出每个末层指标因素的概率分布Pij。

Pij=Nij/N，

(2)

式中：Nij表示把指标因素i归为某一评价级别j的专家人数。

3.5运用CIM模型评估雷达组网探测效能

运用CIM的并联响应模型，逐层求出各级指标因素的概率分布以及运用层次分析法求得各级指标因素的权重值，最后得出所评价对象的概率分布状况。

综上所述，雷达组网探测效能FACIM评估模型可归纳为“三建立两确定一运用”。

4雷达网探测效能实例分析

在西南盆地东部，某地区，地形复杂，现拟在该小部分地区将布置10部雷达，其中雷达体制数为5，工作频段数为10，采用圆弧形配置，雷达组网重叠系数为2，效能费用比略高，极化类型数为4，调制方式数量为7。雷达按工作体制可以分为很多种，假设实例中10部雷达有m种雷达，则雷达体制数为m；10部雷达工作在k个波段，则雷达网的工作频段数为k;该地区中某一块区域同时被n部雷达探测，则雷达网在这块区域的重叠系数为n，其他类似。为了对该组网的探测效能进行评估，采用上述FACIM模型评估其探测效能等级类别的概率分布情况。为此组织从事雷达研究的大学教授、军事研究员等20名组成专家组。具体算法流程如图1所示。

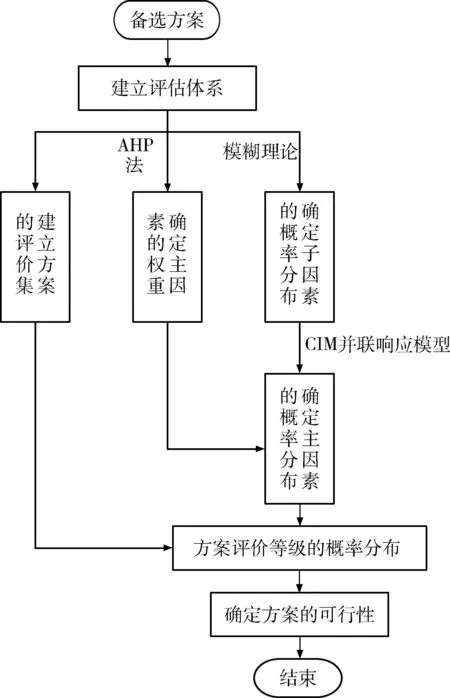
图1　雷达组网探测效能的FACIM评估流程图Fig.1　FACIM evaluation of radar network detection

Step 1：建立雷达组网探测效能评估指标体系。该体系分成3个层次，分别包括6个主因素和24个子因素，具体可见表1。

Step 2：确定因素指标权重值。运用层次分析法来求解权重值时，考虑到其有一个至关重要的步骤—判断矩阵的一致性检验，常常出现判断矩阵不具有满意的一致性，所以这里引入比例系数法来构造判断矩阵，构造出的矩阵具有满意的一致性，其最大特征值对应的特征向量为该矩阵的任一列向量。表2列出了主因素的权重计算过程及计算结果ω=(ω1,ω2,...,ω6)。

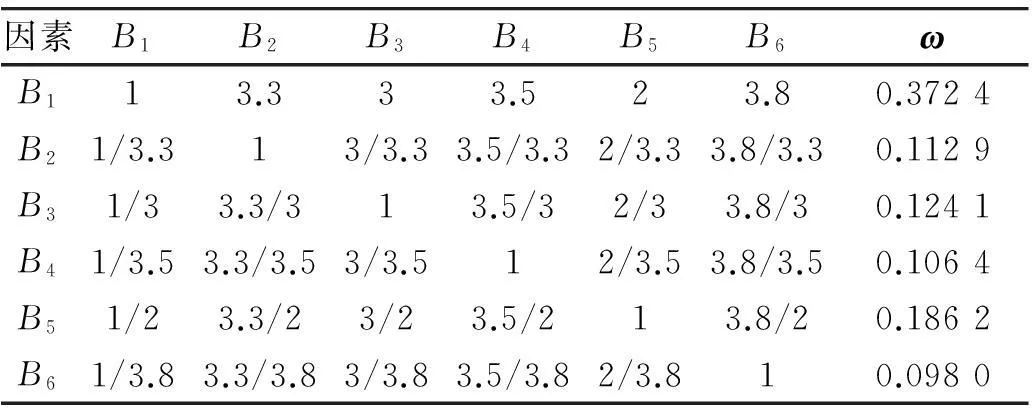
表2　主因素权重计算过程及结果

Step 3：建立雷达组网探测效能评价集V={90～100,80～89,70～79,60～69,60分以下}。

Step 4：确定子因素的概率分布。根据20名专家对每一子因素的评价，由式(2)计算出每一子因素的概率分布。表3给出了上述过程的最终结果。

Step 5：运用CIM并联响应模型，计算各主因素的概率分布。这里只给出目标容量B2的概率分布的计算过程，如表4所示，其余主因素的概率分布可按相同的方法求出。主因素的概率分布见表5。把表5中的概率分布看成一个6×5矩阵A6×5.

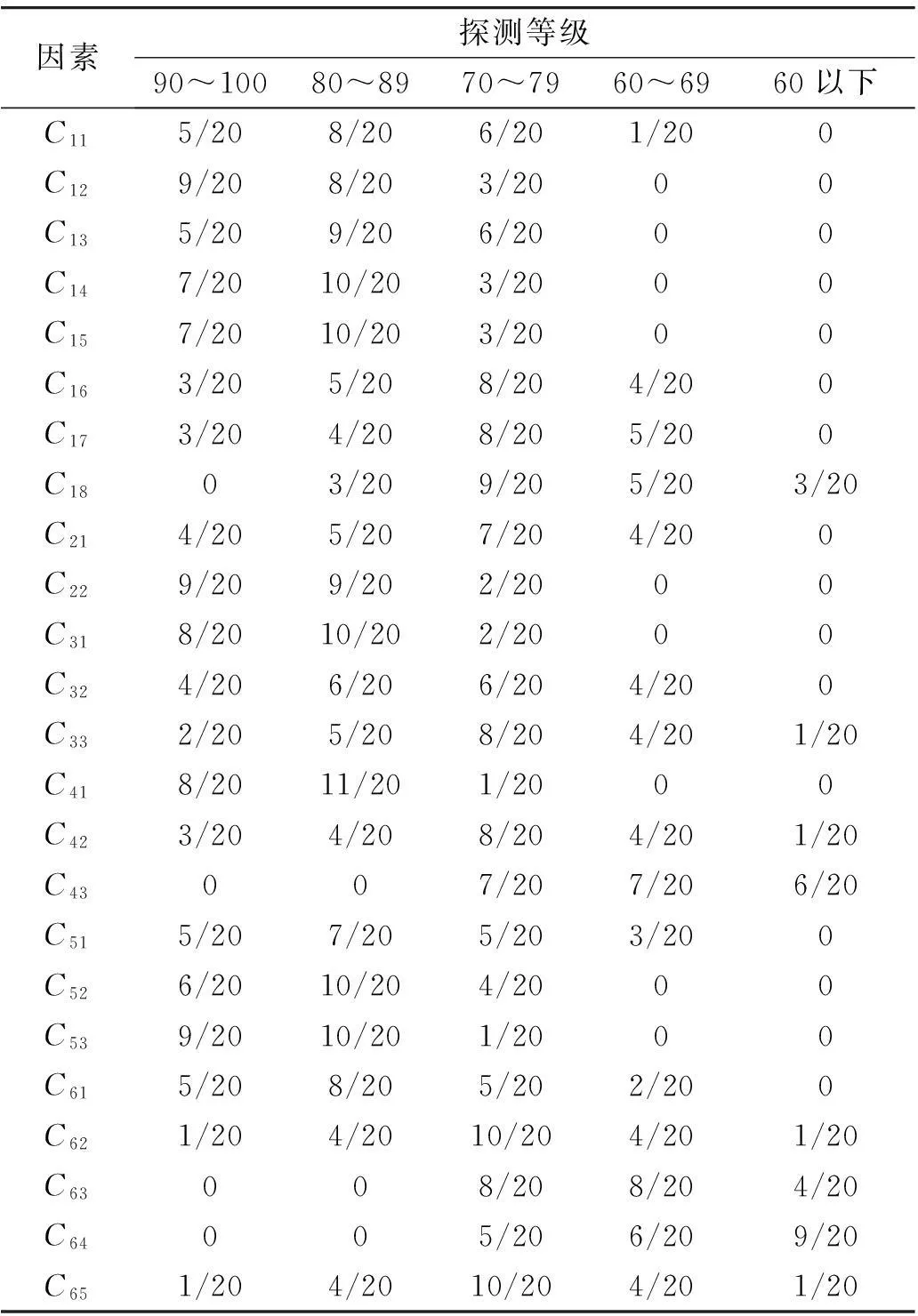
表3　子因素的概率分布

表4　目标容量B2的概率分布计算过程

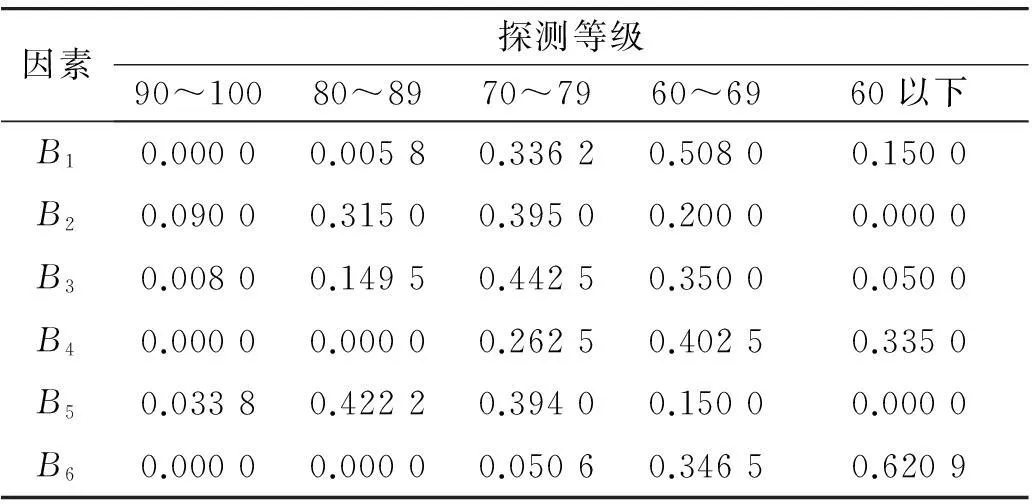
表5　主因素的探测分布

Step 6：把主因素的权重和其对应的评价类的概率分布乘积求和，得到雷达组网探测效能对应评价等级的概率分布PV。

PV=ω·A6×5.

(3)

经计算得到

PV=(0.017 4,0.134 9,0.331 0，0.359 9，0.158 6).

由计算结果可以看出本雷达组网探测效能等级为60～69的可能性最大，概率为35.99%，落在70～79的可能性也很大，概率为33.1%，落在其他等级的概率相对来说可能性较低。这表明该雷达组网探测效能等级在60～69分(按百分制)可能性最大，探测效能能否令人满意可以根据实际情况来分析决定。同时可根据探测任务和目的，可以适当地调整资源以达到想要的效果。

5结束语

提出了一种雷达组网探测效能评估的FACIM模型，由于影响雷达组网探测效能的因素较多，本文从6个方面提出了雷达组网探测效能综合评估指标体系，考虑到若其探测效能越高，投资风险就越低，引入风险分析中的CIM模型来评估雷达组网探测效能，针对体系指标量化难以及单一评估方法的缺陷，在基于模糊理论的基础上，通过层次分析法来确定指标因素的权重值，并对AHP作了改进，即引入比例系数判断矩阵，简化了权重计算，且无需验证矩阵的一致性。最后以西南盆地东部某地区为例进行分析，证实了FACIM模型的可行性和可靠性，同时提高了层次分析法的实用性。

参考文献：

[1]肖文杰, 王健, 卢雷, 等. 含逻辑门的雷达组网作战效能评估研究[J]. 电光与控制, 2010, 17(2): 95-97.

XIAO Wen-jie, WANG Jian, LU Lei, et al. Operational Effectiveness Evaluation of Radar Network With Logic Gates[J]. Eletronics Optics & Control , 2010, 17(2): 95-97.

[2]刘健, 辛永平. 主成分分析的雷达组网作战效能评价模型[J]. 火力与指挥控制, 2011, 36(6): 35-38.

LIU Jian, XIN Yong-ping . Study on Evaluation Model for Networked Radar Operational Effectiveness Based on Principal Component Analysis[J]. Fire Control & Command Control, 2011, 36(6): 35-38.

[3]龙文武, 苏五星, 丁文飞, 等. 基于灰色AHP法的多功能雷达作战效能评估[J]. 现代雷达, 2010, 32(9): 27-30.

LONG Wen-wu, SU Wu-xing, DING Wen-fei, et al. Operational Efficiency Evaluation of Multi-function Radar Based on Grey AHP[J]. Modern Radar, 2010, 32(9): 27-30.

[4]张培珍, 杨根源, 张杨, 等. 雷达组网效能量化评模型[J]. 现代防御技术, 2010, 38(5): 5-10.

ZHANG Pei-zhen, YANG Gen-yuan, ZHANG Yang, et al. Quantitative Evaluation Model for Radar Net Effectiveness[J]. Modern Defence Technology, 2010, 38(5): 5-10.

[5]杨峰, 王碧垚, 赵慧波, 等.基于云模型的战略预警信息系统效能评估[J]. 系统工程与电子技术, 2014, 36(7): 1334-1338.

YANG Feng, WANG Bi-yao, ZHAO Hui-bo, et al. Effectiveness Evaluation for Strategy Early-Warning Information System Based on Cloud Model[J]. Systems Engineering and Electronics, 2014, 36(7): 1334-1338.

[6]刘婧, 冒长礼, 赵呈阳. RBF模糊神经网络在舰载C3I系统效能评估中的应用[J]. 解放军理工大学学报：自然科学版, 2013, 14(6): 674-678.

LIU Jing, MAO Chang-li, ZHAO Cheng-yang. Application of RBF Fuzzy Neural Network in Effectiveness Evaluation of Shipboard C3I System[J]. Journal of PLA University of Science and Technology：Natural Science ed., 2013, 14(6): 674-678.

[7]梁力丹, 郑达, 巨能攀, 等.基于灰色关联与模糊数学的重力式挡土墙震害评估[J]. 工程地质学报, 2014, 22(6): 1234-1240.

LIANG Li-dan, ZHENG Da, JU Neng-pan, et al. Seismic Saety Evaluation of Gravity Retaining Wall Using Grey Correlation and Fuzzy Mathematics[J]. Journal of Engineering Geology, 2014, 22(6): 1234-1240.

[8]王征, 曹田泉. 模糊数学在中国书画评估体系下的应用与研究[J]. 艺术百家, 2014, 138(3): 221-223.

WANG Zheng, CAO Tian-quan. Application of Fuzzy Mathematics in the Evaluation System of Chinese Calling and Painting [J]. Hundred Schools in Arts , 2014, 138(3): 221-223.

[9]苏成, 黄欢, 徐瑞, 等. 大规模非线性系统随机振动显式迭代Monte Carlo模拟法[J].振动工程学报, 2014, 27(2): 159-164.

SU Cheng, HUANG Huan, XU Rui, et al. Random Vibration Analysis of Large-Scale Nonlinear Systems by Explicit Iteration Monte Carlo Simulation Method[J]. Journal of Vibration Engineering, 2014, 27(2): 159-164.

[10]高祺勋, 权聪娜, 李博, 等.灰色模糊CIM模型的电力项目融资风险评判构架[J]. 工业工程, 2010, 13(4): 96-99.

GAOQi-xun,QUANCong-na,LIBo,etal.FinancingRiskAssessmentofPowerPlantConstructionbyUsingGreyFuzzyCIMModel[J].IndustrialEngineeringJournal, 2010, 13(4): 96-99.

[11]张沅. 基于粗糙集和模糊理论的房地产风险[D].广西：广西大学, 2010.

ZHANGYuan.ResearchofRealEstateRiskEvaluationModelBasedonRoundSet&FuzzySetTheory[D].Guangxi:GuangxiUniversity, 2010.

[12]游永彬, 周延年, 郑玉山. 基于二元语义层次分析法的主观权重确定算法[J]. 西北工业大学学报，2013,31(5):710-715.

YOUYong-bin,ZHOUYan-nian,ZHENGYu-shan.ANewandEffectiveMethodforDeterminingSubjectiveWeightofIndexBasedonTwo-TupleLinguisticAHP[J].JournalofNorthwesternPolytechnicalUniversity, 2013,31(5):710-715.

[13]SUNLu.AMin-MaxOptimizationApproachforWeightDeterminationinAnalyticHierarchyProcess[J].JournalofSoutheastUniversity(EnglishEdition), 2012, 28(2):245-250.

[14]鲁丹，张金月. 基于层次分析法的BIM内容库网站评价研究[J]. 图学学报,2015,36(2):298-305.

LUDan,ZHANGJin-yue.AHP-BasedEvaluationofBIMContentLibraryWebsites[J].JournalofGraphics, 2015, 36(2):298-305.

[15]黄德才, 胥琳.AHP法中判断矩阵的比例标度构造法[J]. 控制与决策, 2002,17(4): 484-486.

HUANGDe-cai,XULin.ProportionCriteriaandMethodforBuildingComparisonMatricesintheAnalyticHierarchyProcess[J].ControlandDecision,2002,17(4): 484-486.

Evaluation on Radar Network Detection

CUI Yu-juan , CHA Hao

( Naval University of Engineering, College of Electronics Engineering,Hubei Wuhan 430033, China)

Abstract:The evaluation index system on efficiency of radar network detection is established on the basis of construction principles. These indexes are difficult to quantify directly and prone to fuzzy evaluation, they have a multi-level structure. Based on fuzzy theory and analytic hierarchy process method, the model of controlled intervals and memory is applied into radar network detection evaluation. Finally, an example is used as the illustration, the effectiveness and utility of the controlled interval and memory model is verified, which lays a foundation for optimization deployment of radar network.

Key words:radar network; detection effectiveness; fuzzy theory; analytic hierarchy process; controll intervals and memory model；optimization deployment

*收稿日期：2015-06-11；修回日期：2015-09-01

作者简介：崔玉娟(1984-)，女，江苏徐州人。助工，博士生，主要从事雷达组网，智能算法，探测效能评估。

通信地址：430033湖北省武汉市解放大道717号239信箱E-mail：xiaoxiao926878@126.com

doi:10.3969/j.issn.1009-086x.2016.03.002

中图分类号：TN95

文献标志码：A

文章编号：1009-086X(2016)-03-0007-05

空天防御体系与武器