基于最大最小贴近度和GIOWA算子的上证综指的组合预测模型应用

施文月，　　袁宏俊

(安徽财经大学 统计与应用数学学院，安徽 蚌埠　233000)



基于最大最小贴近度和GIOWA算子的上证综指的组合预测模型应用

施文月，袁宏俊

(安徽财经大学 统计与应用数学学院，安徽 蚌埠233000)

摘要：为了能更准确地把握我国股票价格的走向，首先使用传统的多元回归模型、指数平滑模型和ARIMA模型分别对2014年1月-12月的上证综合指数的月末价收盘价进行预测，然后在此基础上采用基于最大最小贴近度的广义诱导有序加权算术平均(GIOWA)算子的组合预测方法将三种模型整合，再对上证指数价格数据进行运算，得出每种方法所占权重和预测值，最后通过比较评价体系的各个指标发现基于最大最小贴近度和GIOWA算子的组合预测方法的精度更令人满意.

关键词：最大最小贴近度；GIOWA算子；组合预测；股票价格

1引言

从1990年我国第一个证券交易所在上海正式成立至今，我国股市发展迅速，在此期间股市行情也经历了大起大落，从2006年至2008年，股价变动剧烈，并在2015年股价的变动极不正常，阻碍了证券市场的健康发展和投资者们的正确决策.因此，投资者更需具备正确预测股票价格走势的能力.

自从股市产生至今，大量的学者对股票价格的预测产生了极大的关注.在以往的文献中，学者们大都采取单项预测方法.Engle(1982)[1]首次使用ARCH模型来预测事物的发展.李攀峰(1997)[2]首次使用灰色系统理论预测股票价格走势.罗阳、杨桂元(2013)[3]基于ARCH和GARCH模型，利用类GARCH模型对股市的非对称性进行了研究.

现在越来越多的学者采用组合预测的方法来研究事物的发展.吴良平、张健和陆媛(2011)[4]运用基于IOWHA算子的组合预测研究了我国入境旅游人数.莫颂娟、杨桂元和罗阳(2015)[5]利用IOWGA算子测算了我国GDP总量的变化.林义征、袁宏俊和宋马林(2016)[6]通过IOWHA算子与向量夹角余弦构建了区间组合预测模型.

本文先分别建立多元回归模型、指数平滑模型和ARIMA模型对我国股票价格进行预测.再采用最大最小贴近度[7]的GIOWA算子模型对股票价格进行组合预测，并分别对几种预测方法进行评价.

2模型的建立

2.1单项预测方法介绍

2.1.1多元回归模型

根据杨树成(2006)[8]的研究，股票价格与当日股票最高价、最低价和成交量有关，故分别选取作为自变量.预测的模型如下式(1)所示.

(1)

2.1.2指数平滑模型

指数平滑法(Exponential Smoothing)由布朗提出.由于序列本身具有稳定性，一定时间内序列的外在特征能够延续，所有一定程度上可以递推序列发展的走势.鉴于近期的序列对目前的状态会有较大的影响，故越近期的状态占有越大的比重.指数平滑兼具了算术平均和移动平均的优点.

2.1.3ARIMA(p，d，q)模型

ARIMA模型全称为自回归移动平均模型.模型公式表示为：

(2)

其中Φ(L)=(1-φ1L-φ2L2-…-φPLP)，Θ(L)=(1-θ1L-θ2L2-…-θqLq).

2.2相关概念介绍

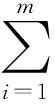
本文中采用单项预测方法的预测精度为组合预测的诱导值，则预测精度公式如下：

(3)

2.2.1GIOWA算子的定义

GIOWA算子又称广义诱导有序加权算术平均算子，模型表示为:

(4)

其中xti为t时刻第i中预测方法的预测值，uti为xti的诱导值.ω为广义系数，取值范围(-∞,0)∪(0,∞).当ω=1时，GIOWA算子转化为IOWA算子；当ω=-1时，GIOWA算子转化为IOWHA算子.

2.2.2最大最小贴近度的定义

设A、B为实数序列，最大最小贴近度Γ：

(5)

其中∧，∨分别为取小、取大算子.贴近度刻画了两组数据的接近程度，取值范围[0，1]，当Γ取值趋于越大时说明两组数据关系密切，反之则说明接近程度低.

为了能更便捷地比较预测方法的有效性，首先对数据进行无量纲化(归一化)处理：

其中maxt=max{xt,x1t,x2t,…xmt}，mint=min{xt,x1t,x2t，…xmt}.

2.3组合预测模型的建立

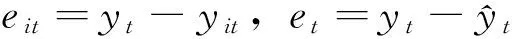
(6)

我们希望Γ(l1,l2,…,lm)越大越好，Γ(l1,l2,…,lm)越大表示组合预测方法越有效.故基于最大最小贴近度的GIOWA算子的最优组合预测模型可以表示为：

(7)

2.4预测误差评价体系

为了衡量各种预测方法的有效性，本文选取五项指标构建预测误差评价体系：

3我国上证股票价格的组合预测

3.1数据来源

本文选取2014年1月到12月的上证综合指数的月末收盘价、最高价、最低价以及成交量作为研究样本，数据来源于上海证券交易所网站.

3.2实证分析

首先，将数据进行多元回归模型拟合，由于在拟合过程中发现股票最低价对收盘价的影响不显著，故剔除该变量.得到得方程如式(8)所示.

yt=x1+0.000014x2

(324.04)(4.55)

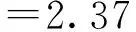
(8)

接着，拟合ARIMA(p，d，q)模型.首先需要判断数据的平稳性，根据ADF检验发现数据存在单位根，对数据进行一阶差分后检验发现数据平稳.通过观察数据的自相关图和偏自相关图，判断数据属于自回归模型，结合AIC和BIC准则选取p等于1，故最后的模型ARIMA(1，1，0)如式(9)所示.

(9)

根据三种单项预测方法可求得的预测值，并根据式(3)计算得出精度，整理如表1所示.

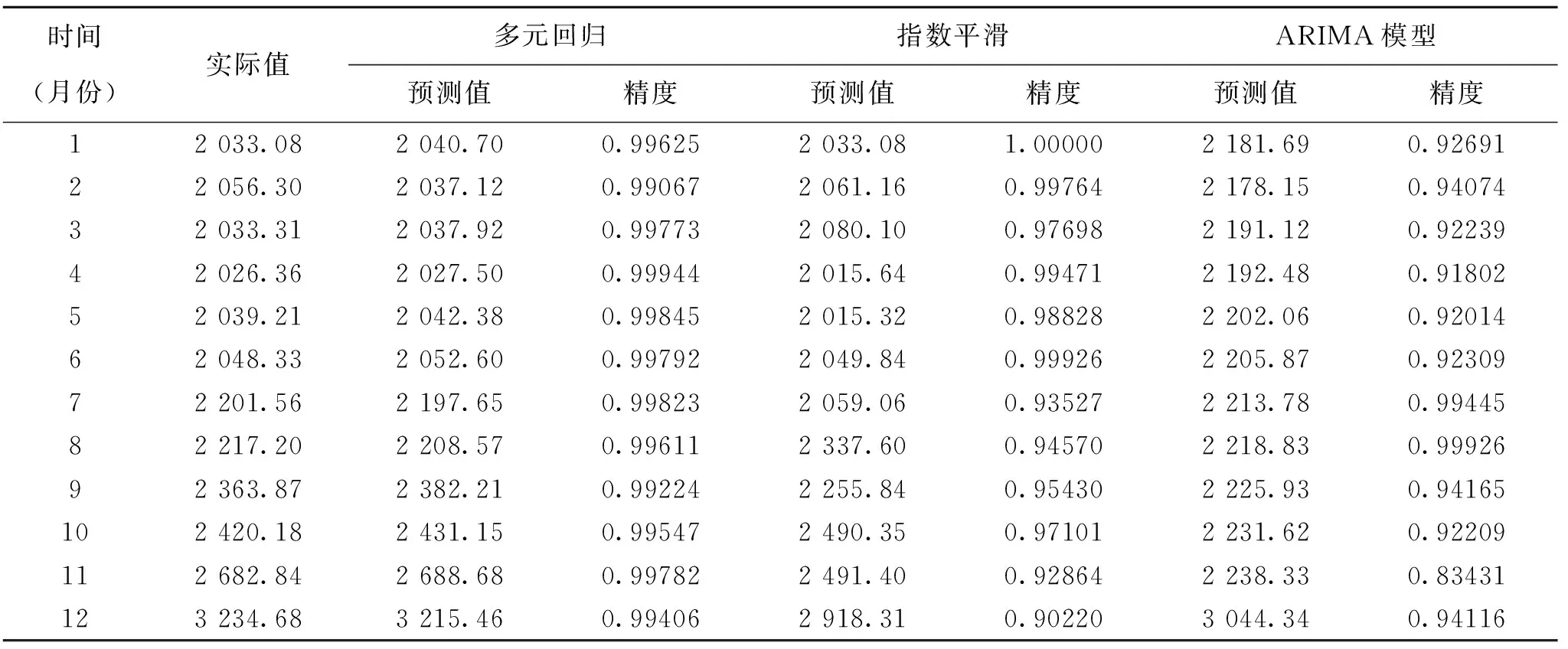
表1　各单项预测值及精度

根据表1，按照精度从大到小的顺序，将每一时刻预测值的位置进行调整，并且对真实值和调整后的数据进行归一化处理，整理如表2所示.

表2　数据的归一化处理

将数据代入模型式(7)，运用lingo软件求解.本文中对ω分别取了20个不同的值，通过对比发现当且仅当ω=1时，最大最小贴近度取得最大值0.9326，此时，l1=0.9703，l2=0.0297，l3=0.根据权重系数可求得组合预测的预测值，整理如表3所示.

表3　组合预测值及精度

为了比较各种预测方法和组合预测方法的优劣，根据实际值和以上四种方法得到的预测值可算出每种预测方法预测效果评价指标值，整理如表4所示.

表4　预测误差评价结果

通过表4可发现，组合预测在所有评价指标上的值均小于前三种单项预测方法，由此证明基于最大最小贴近度和GIOWA算子的组合预测方法效果是较优的.

4结论

本文以上证综和指数的月末收盘价为研究样本，选取多元回归模型、指数平滑模型和ARIMA模型三种预测方法建立了基于最大最小贴近度的GIOWA组合预测模型.通过比较各项评价指标可知：较其他三种单项预测方法，组合预测的预测能力最好，模型效果最优，能有效降低股票的预测误差.故基于最大最小贴近度的GIOWA组合模型为我们进行股票价格预测提供了一定的依据，在解决实际经济问题上具有很好的现实意义.

参考文献：

[1]Engle R E.Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of United Kingdom Inflation[J].Econometrica,1982(4):987-1007.

[2]李攀峰.股票价格的灰色预测[J].华东经济管理,1997(4):60-61.

[3]罗阳,杨桂元.基GARCH类模型的上证股市波动性研究[J].统计与决策,2013(12):162-165.

[4]吴良平,张健,陆媛.基于IOWHA算子的组合预测在中国入境旅游中的应用分析[J].旅游学刊,2011(11):19-27.

[5]莫颂娟,杨桂元,罗阳.基于IOWGA算子的中国GDP总量的组合预测[J].统计与决策,2015(16):4-7.

[6]林义征,袁宏俊,宋马林.基于IOWHA算子与向量夹角余弦的联系数型区间组合预测[J].统计与决策,2016(5),84-86.

[7]袁宏俊,杨桂元.基于最大—最小贴近度的最优组合预测模型[J].运筹与管理,2010(2):116-122.

[8]杨树成.上证综合指数(日收盘)线性回归模型[J].天津农学院学报,2006(1):27-31.

Shanghai Composite Index Forecast Model Based on the Biggest-smallest Approach Degree and GIOWA Operator

SHI Wen-yue,YUAN Hong-jun

(InstituteofStatisticsandAppliedMathematics,AnhuiUniversityofFinanceandEconomics,Bengbu,Anhui233000)

Abstract：In order to predict the stock price more accurately,we first used the traditional multiple regression model,exponential smoothing and ARIMA model to predict the price of Shanghai composite index from January to December 2014.Then based on the biggest-smallest approach degree of GIOWA operator combination forecasting method,the Shanghai index price data,the weights and forecast value of each method is explored.Finally it has made more than every single prediction,which shows more excellent and stable results,and the method is applied to predict the price of Shanghai composite index.

Key words：biggest—smallest approach degree；GIOWA operator；combination forecast；stock price

收稿日期：2016-04-07

作者简介：施文月，1993年生，女，安徽滁州人，硕士研究生，研究方向：经济统计学；

中图分类号：F201

文献标识码：A

文章编号：1671-9743(2016)05-0020-05

袁宏俊，1978年生，男，安徽庐江人，副教授，硕士生导师，研究方向：数量经济学.