圆梯中梯图的亏格分布

曾建初

(昆明理工大学 学报编辑部,云南 昆明　650500)



圆梯中梯图的亏格分布

曾建初

(昆明理工大学 学报编辑部,云南 昆明650500)

摘要：近几十年来，拓扑图论都是数学研究的一个重要领域,计算图的亏格分布是拓扑图论中的一个热点内容.该文对图的可定向亏格分布问题进行了研究，应用联树模型的方法,计算了一类新的3-正则图——圆梯中梯图的亏格分布.

关键词：联树模型;亏格分布;圆梯中梯图

0引言

近几十年来，拓扑图论都是数学研究的一个重要领域,计算图的亏格分布是拓扑图论中的一个热点内容.人们研究图的亏格分布,发现了很的数学方法.如刘彦佩教授联树模型[1-2].Mohar教授的矩阵模型[3].张湘林等[4]用迭代粘合法计算了一类5-正则图的亏格分布..本文以联树模[1-2]为工具,受文献[1-13]思想的启发,计算了圆梯中梯图——一类新的3-正则图的亏格分布.如无特别说明,本文所说的亏格分布都是可定向的亏格分布.

1预备知识

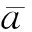
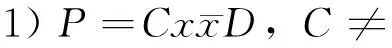
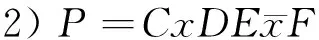
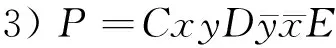
引理1[1]设B,C,D,E,F是多边形P的边对应的带符号的字母的线性排列,则

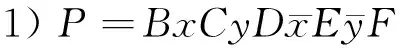
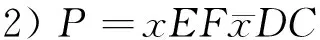
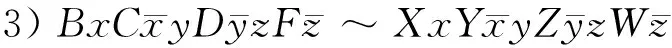
任何一个曲面,其多边形表示都有唯一的一个标准形式:

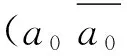
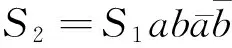
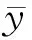
引理3[1]任何图G总能被嵌入可定向曲面.设n(G)为图G在可定向曲面上不同嵌入的数目,则

这里:ni是度数为i的顶点的个数.

引理4[1]图G在亏格为p的曲面上嵌入的数目,与树T的选取无关.

gi(G)表示图G在亏格为i(i≥0)可定向曲面上的不同嵌入的数目,图G的可定向亏格分布多项式是:

这里n是图G的参数.需要进一步了解的概念参见文献[1].

2主要结果

把一个圆梯的每一条梯边从中剖开,嵌入1个梯,这样所形成的图形叫做圆梯中梯图,图1是n+1条梯边的圆梯中梯图,记为Gn+1.图2表示图Gn+1的一个联树Jn.

图1　圆梯图Gn+1

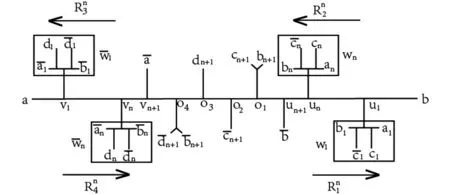
图2　图Gn+1的一个联树Jn

根据联树(joint tree)Jn,有

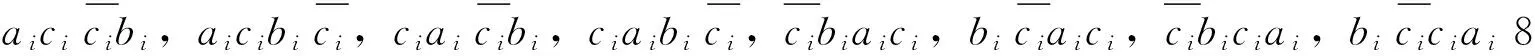
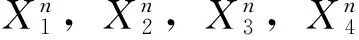
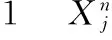
表与之间关系表

引入如下3个映射ψi(i=1,2,3)[2]:

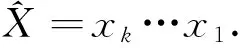
我们能够把圆梯中梯图的关联曲面化简为下面11类(a,b,c是不同的符号)：

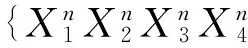
经过计算,获得

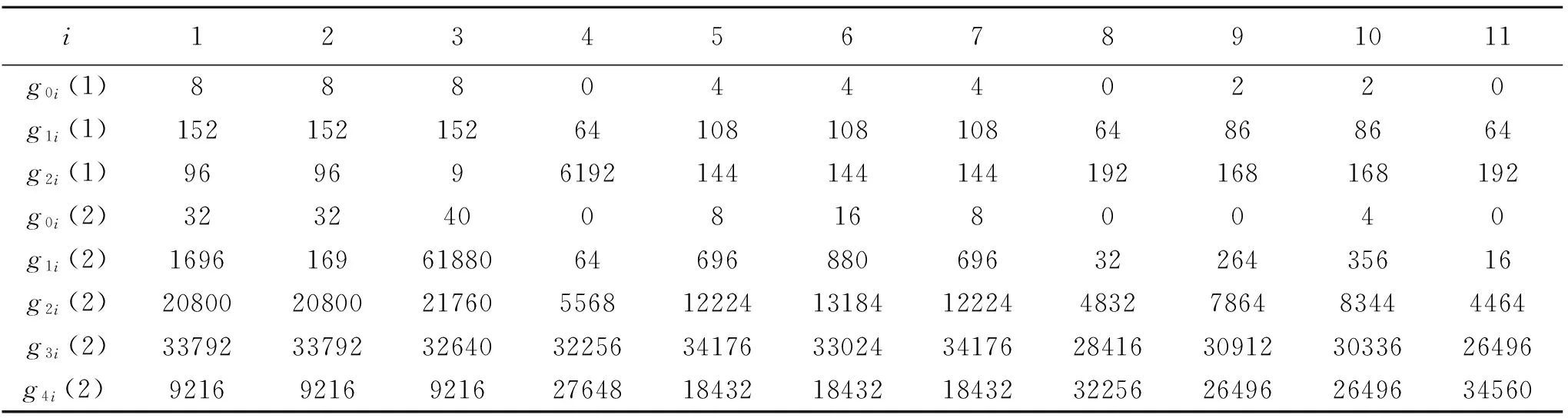
表1

定理2圆梯中梯图Gn+1的联树对应的关联曲面是下面的28=256类:

圆梯中梯图Gn+1的亏格多项式是:

其中:C0=4g09(n)+4g010(n)+56g011(n),C1=4g19(n)+4g110(n)+56g111(n)+48g09(n)+48g010(n)+96g011(n),…,C2n=4g(2n)9(n)+4g(2n)10(n)+56g(2n)11(n)+48g(2n-1)9(n)+48g(2n-1)10(n)+96g(2n-1)11(n),C2n+1=48g(2n)9(n)+48g(2n)10(n)+96g(2n)11(n)

当n=1时,

C0=4×2+4×2+56×0=16

C1=4×86+4×86+56×64+48×2+48×2+96×0=4464

C2=4×168+4×168+56×192+48×(86+86)+96×64=26496

C3=48×(168+168)+96×192=34560

fG2(x)=16+4464x+26496x2+34560x3

当n=2时,

C0=16,C1=3568,C2=346112,C3=2935296

C4=7630848,C5=5861376

fG3(x)=16+3568x+346112x2+2935296x3+7630848x4+5861376x5

参考文献：

[1]Yanpei Liu.Theory of Polyhedra[M].Beijing:Science press,2007.

[2]Wan L X,Liu Y P.On the embedding genus distribution of ladders and crosses[J].Applied mathematics letters,2009(22):738-742.

[3]Mohar B.An obstruction to embedding graphs in surfaces[J].Discrete math,1989(78):135-142.

[4]张湘林,黄元秋,郭婷.一类5-正则外平面图的亏格分布[J].应用数学学报,2015(5):133-144.

[5]Zeng J,Liu Y,Hao R.Counting Orientable Embeddings by Genus for a Type of 3-Regular Graph[J].Graphs & Combinatorics,2012(1):133-142.

[6]任韩.曲面上图染色综述(上)[J].昆明理工大学学报:自然科学版,2016(1):130-148.

[7]刘彦佩.我所认识的拓扑图论(Ⅰ):球面上十部曲[J].2013(1):105-108.

[8]谭秋月.若干图类的平衡指标集[J].昆明理工大学学报:自然科学版,2014(6):136-140.

[9]吴跃生.非连通并图I(K_(m,n))∪G的优美标号[J].昆明理工大学学报:自然科学版,2015(2):142-146.

[10]马京成，马登举，朱王君.3-正则Halin图的完美匹配数[J].昆明理工大学学报:自然科学版,2015(5):132-136.

[11]任韩.曲面上图染色综述(下)[J].昆明理工大学学报:自然科学版,2016(2):134-148.

[12]郝荣霞，李文俏，刘峰.梯图的线图的Tutte唯一性[J].昆明理工大学学报：自然科学版,2012(4):98-102.

[13]任韩，镡松龄，马登举.稠密图的三角剖分嵌入[J].昆明理工大学学报：自然科学版,2012(2):89-93.

Genus Distribution of Ladder of Circular Ladder Graphs

ZENG Jian-chu

(EditorialDepartmentofJournalofKunmingUniversityofScienceandTechnology,Kunming,Yunnan650500)

Abstract：In recent decades,topological graph theory has been an important field of mathematical research.Calculating the orientable genus distribution of graphs is a hot issue.In this paper,the orientable genus distribution of a class of graphs was studied by applying the method of the joint tree model,calculating the genus distribution of a new class of 3-regular graphs,ladder of circular ladder graphs.

Key words：joint tree model；orientable genus distribution；ladder of circular ladder graphs

收稿日期：2016-01-01

基金项目:云南省人才培养项目(KKSY201213063).

作者简介：曾建初，1964年生,男,湖南涟源人,副教授，博士,研究方向:拓扑图论.

中图分类号：O157.5

文献标识码：A

文章编号：1671-9743(2016)05-0015-05