一块水泥混凝土路面板块表面曲面方程的推导及其特性
2016-07-18张儒雅
张儒雅
(上海民航新时代机场设计研究院有限公司 上海 200335)
一块水泥混凝土路面板块表面曲面方程的推导及其特性
张儒雅
(上海民航新时代机场设计研究院有限公司 上海 200335)
本文通过对施工状况的简化和抽象,推导出了一块水泥混凝土路面板块表面的曲面方程。该方程为二次函数。随后讨论了该曲面的等高线、坡度等特性。最后根据该曲面方程的特性对其在工程上的实际应用提出了建议。
水泥混凝土路面;摊铺;表面曲面;曲面方程;二次曲面;等高线;双曲线;内插;坡度
1 问题的提出
目前我国水泥混凝土路面或机场道面面层多采用两侧立模板现场浇筑的方式施工,如图1、2所示。通常情况下,在面层板块一对相互平行的长边上立模板,控制每条模板两个端点也就是板块四个角点的高程,然后向两条模板之间浇入混凝土,振捣密实后采用垂直于模板的圆柱形滚筒或摊铺机整平模块对混凝土表面进行初步找平,而后经人工精平后成型,后续再进行拉毛、切缝、刻槽等其他工序。

图1 传统人工方式施工水泥混凝土面层场景

图2 摊铺机施工水泥混凝土面层场景
在不考虑滚筒或摊铺机整平模块竖向挠度的大前提下,如果每条模板的两个端点间的高差相同,那么这块水泥混凝土板块表面显然为一平面。但在实际情况中却存在两模板端点高差不同的情况,如道路的超高渐变段、交叉口等横坡变化处,机场道面的道口、机坪内的扭坡段等等。从直觉上想象,这些部位的水泥混凝土板块表面应该为一曲面,这就提出了此曲面的方程为何,有何特性等问题。接下来本文将推导此曲面的解析方程,并结合工程上的实际应用对其特性进行初步探讨。
2 板块表面曲面方程的推导
2.1 问题的简化和抽象
以一块板块的某一角点O为原点建立坐标系。为便于该曲面等高线的讨论,以过O点的水平面为Oxy平面,y轴为模板方向,x轴与之垂直,z轴竖直向上,如图3所示。板块的另外三个角点分别为A、B、C,那么直线OA和BC分别代表两条模板,设P为OA上的动点,Q为BC上的动点,且动直线PQ始终与y轴垂直,即平行于Oxz平面。当滚筒或整平模块(不考虑竖向挠度)在模板上前后运动时,相当于动直线PQ沿OA和BC运动,那么动直线PQ运动所形成的曲面即为所求的板块表面曲面OACB。
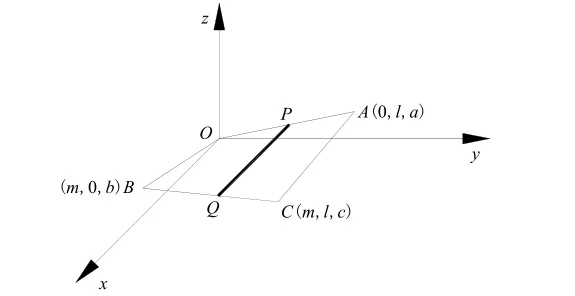
图3 板块曲面推导简图
2.2 曲面方程的推导
设所讨论的一块板块长度(沿模板方向)为l,宽度为m,角点A、B、C与O点的高差分别为a,b,c。那么点A、B、C的坐标就分别为(0,l,a)、(m,0,b)、(m,l,c),则向量={0,l,a},向量={0,l,c-b}。
所以直线OA的参数方程为[1]:
(t为参数)
直线BC的参数方程为[1]:
(t为参数)
由于动直线PQ始终与y轴垂直,即点P、Q的y坐标应相同,因此可设点P、Q的坐标分别为(0,tl,ta)、(m,tl,b+t(c-b))。故向量={m,0,b+t(c-b-a)},所以动直线PQ的参数方程为[1]:
(s、t为参数)
上式即所求曲面OACB的参数方程,消去式中的参数s、t,即得到该曲面一般方程为:
由此可见,所求曲面为二次曲面,下面继续探讨其特性。
3 所求曲面的特性
上述曲面的推导过程虽然是由水泥混凝土板块浇筑的实际情况引出的,但推导过程中并未对其中所使用参数和自变量x,y的正负或取值范围进行限制,因此该曲面方程在满足l≠0且m≠0的大前提下各参数和自变量x,y可取任意实数值。由此我们可以得出以下几点该曲面的重要性质。
(1)该曲面与平面x=x0或y=y0相交的交线均为直线。
(2)该曲面与平面z=z0相交的曲线方程为:
当c-b-a≠0时该曲线为一双曲线,其渐进线为z=z0平面上的两条直线:
该两直线的位置与 z0的取值无关,也即本文所讨论曲面的等高线为一族以上述两条直线为渐进线的双曲线。
(3)当c-b-a=0即∥时该曲线退化为平面,其等高线也变为直线。
(4)为考察该曲面沿x,y方向的坡度,分别取两个方向的偏导数得到:
由此可知,该曲面沿某个方向的偏导数与该方向自变量取值无关,也即该方向的坡度为定值,这也从另一方面验证了性质(1)。当c-b-a≠0时,令两个方向的偏导数均等于零可以求得一点(),该点在两个方向上的坡度均为零,该点同时也是曲面等高线所组成的双曲线族的两条渐进线的交点。
下面分别为其三维图像和平面等高线图[2],可以明显的看出其相关特性。

图4 曲面三维图像(l=5,m=4,a=-1,b=-1,c=2)
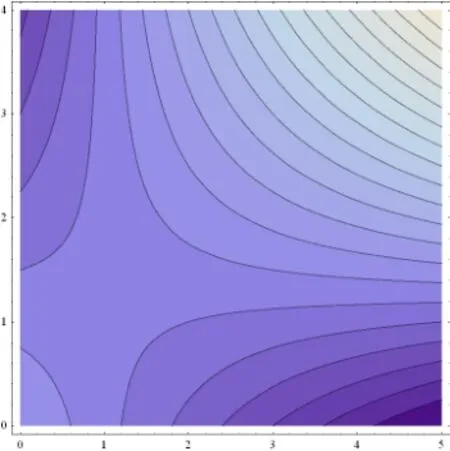
图5 曲面等高线图(l=5,m=4,a=-1,b=-1,c=2)
4 工程上实际应用
基于上述曲面的解析方程和性质讨论,在工程实际中对水泥混凝土板块的设计和施工可以得到以下几点实际用途:
(1)在已知四个角点高程的前提下,板块上任意一点的高程均可通过直线内插的方式求出,而且采用任一组相互平行的边内插出的高程结果相同。
(2)为防止板块积水,设计时尽量避免两个方向坡度均为零的点位于板块中,即尽量避免点()位于曲面OACB内部。
[1]同济大学数学系,高等数学第六版,高等教育出版社,2007;
[2]丁大正,Mathematica基础与应用,电子工业出版社,2013。
U45
B
1007-6344(2016)07-0021-01
张儒雅(1981~),男,汉族,工程师,目前于上海民航新时代机场设计研究院有限公司从事机场设计工作。
