基于测量设备无关协议的量子身份认证方案

董颖娣，彭进业，张晓博，张振龙



基于测量设备无关协议的量子身份认证方案

董颖娣1,2，彭进业1，张晓博1，张振龙2

（1. 西北工业大学电子信息学院，陕西西安 710072；2. 西安建筑科技大学信息与控制工程学院，陕西西安710055）

借助测量设备无关量子密钥分配协议的安全性，提出了测量设备无关的量子身份认证协议。在此协议下，认证中心和认证方以共享密钥加密认证信息和认证密钥，将其发送至第三方进行贝尔态测量以提取安全的认证信息，实现认证中心对认证方有效认证，并更新共享密钥。分析协议性能显示，系统在不同攻击下认证过程是安全且有效的。

量子身份认证；量子密钥分配；测量设备无关；贝尔态测量

1 引言

量子密钥分配(QKD, quantum key distribution)协议以量子力学和量子信息论框架中的无条件安全性[1,2]已成为国内外的研究热点[3,4]。量子身份认证(QIA, quantum identity authentication)作为QKD系统的重要分支，检测QKD协议中通信双方的假冒行为，防止量子比特被攻击者非法获取导致合法用户信息安全性下降。QIA是QKD系统获取安全密钥的前提，为通信双方身份合法性提供重要依据。QIA利用量子不可克隆性及量子测不准原理[5]对输入者个人信息进行某种方式的处理并与系统中预先存储的个人信息进行比较，从而对个人身份进行肯定或者否定的判定。在此，要求身份认证系统的三重组合[6]中（I为示证者个人信息集合；T为信息处理系统；D为数据库系统）至少有一个具有量子特征，当认证系统三重组合均为量子特征时，即为纯量子身份认证系统。

1999年，Dusek等[7]首先提出用经典信息认证算法对量子密钥系统经典消息进行认证的方案，从而达到抗干扰信道的效果，但方案没有充分利用量子的物理性质。2000年，曾贵华[8,9]利用量子的物理特性，提出了可信赖中心的QIA，在此基础上进一步研究了无可信赖中心的量子身份认证方案，此方案采用认证密钥加密认证者量子信息以实现对认证方的动态认证过程，认证顺序进行了改进，代替了经典公钥认证方案，弥补了之前方案的不足，但算法过于复杂。同年，周南润等[10]以量子纠缠交换及远距传输的相关性提出了跨中心量子身份认证方案，解决了分布式量子网络中的身份认证问题。2005年，杨宇光等[11]提出一种多用户量子身份认证和密钥分配方案，该方案利用EPR 纠缠态和可信服务器实现网络中用户之间的身份认证和密钥分配，但需要对纠缠态存储。张哲砷等[12]提出一个基于ping-pong协议量子身份认证方案，该方案安全地实现了认证密钥的更新。2009年，张兴兰[13]提出一种基于公钥的量子身份认证方案，方案利用可信的认证中心(CA)完成认证，但是该方案的认证过程比较简单不适合在网络中应用。2010年，李渊华[14]提出基于W态的跨中心的量子身份认证方案，实现了客户在分布式量子通信网络中的身份认证。除以上介绍的量子认证方案，利用量子态的非正交性、纠缠态及GHZ态进行量子身份认证及量子多方身份认证[15~17]也已相继展开。

然而以上所提身份认证过程均在QKD系统中实现，由于QKD系统探测单元存在各种非完美性，使系统存在一定的安全漏洞，如针对探测器非完美性的伪态攻击[18]、时移攻击[19]、致盲攻击等，导致认证信息不安全，认证安全性低。为了建立更加安全、高效的身份认证过程，本文提出了基于测量设备无关量子密钥分配协议[20]的量子身份认证(MDI-QIA, measurement-device-independent QIA)方案。在MDI-QIA系统中，认证中心和认证方转换共享密钥后对认证信息和认证密钥加密，将量子信息通过量子门加密后发送到不可信第三方（measurement unit），在第三方以分束器、偏振分束器及探测器完成量子态的贝尔测量，并以公开信道公布测量结果；认证中心通过基对比获取认证信息，以此完成对认证方的认证。本文借助测量设备无关协议完成身份认证过程，以此去除认证过程的量子边带攻击，提高认证信息的安全性。

本文主要目的是实现量子测量设备无关协议框架下的身份认证过程。首先刻画出量子身份认证过程框架，并细化了认证协议的步骤；对所提方案进行安全性和有效性分析；数值仿真结果表示该协议在不同攻击下是均是安全的。此研究是测量设备无关技术于身份认证中的典型应用，研究成果对量子保密通信的发展具有一定的推动意义。

2 协议描述

1) 准备阶段

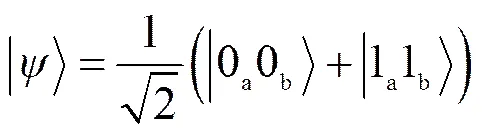
2) 认证密钥的转换

3) 认证过程

量子身份认证框架下，Alice为可信认证中心，Bob为需要认证的用户，不可信第三方为参与认证过程的辅助方，实现量子贝尔态测量及转发，测量设备无关协议框架下的量子身份认证过程如图1所示。

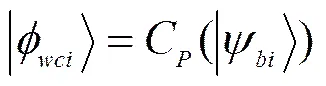
(3)

其中，表示单位矩阵，表示Hardmard矩阵，和表示泡利矩阵。同理，通过量子逻辑门作用后量子态为。

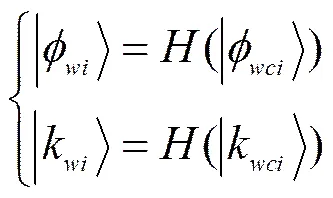
图2 量子逻辑门框架

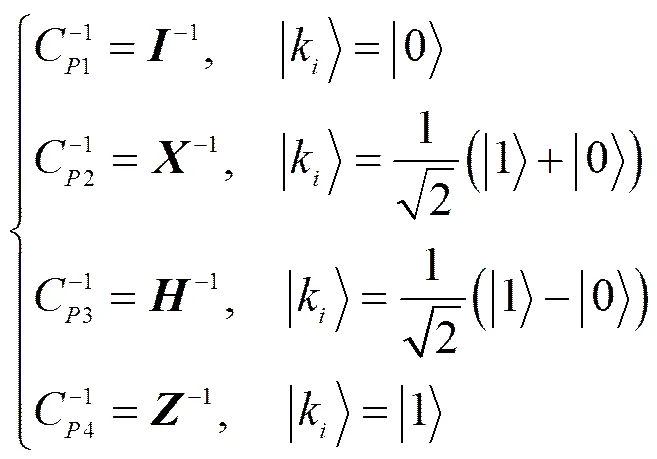
Step5 在量子测量单元采用同样测量算符对及量子态投影测量[22]，如式(6)所示。

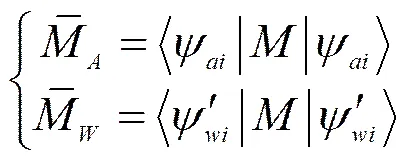
3 安全性分析及协议效率

安全性分析是判断身份认证过程是否正确的判断标准。协议从经典攻击和量子攻击2方面研究所提方案的安全性，并讨论身份认证的初始阶段及认证阶段的安全性能；最后讨论了协议的执行效率。

3.1 协议攻击分析

在经典攻击策略条件下，攻击者以中间人方式攻击信道，或者借助合法通信者间的经典过程窃取信息，从而获得所谓的边信息[9]。量子密码通信过程中假定攻击者是不能同时获得量子信道和经典信道的信息，即使攻击者得到不可信第三方的贝尔态测量后经典信息，由于测量设备无关协议的安全属性，攻击者即使得到经典信息也无法精确得到认证中心Alice及认证方Bob中发送的量子态信息，即无法精确获取认证密钥及认证信息，从而无法实现攻击策略。

在量子攻击条件下，在量子身份认证的初始阶段，攻击者Eve以截获攻击共享密钥，由于共享密钥采用非正交的量子比特，由量子不可克隆定理及量子力学的测不准原理保证，攻击者不能同时精确复制非正交的量子比特，即不诚实的攻击者不能复制Alice与Bob之间共享密钥，从而保证了后继认证过程的安全性。

在量子认证阶段，攻击者以截获/重发攻击或者纠缠攻击获取信息。首先分析截/转发攻击，假设窃听者Eve以幺正操作截获Bob的认证信息，但认证信息是以共享密钥加密的，由于Eve无法获取共享密钥，则其无法精确得到Bob认证信息。

由于纠缠攻击比其他攻击更具有威胁性[23]，其认证方与认证中心之间的交互的密钥率最低，考虑在此攻击条件下的系统安全密钥率更具有可行性。在MDI-QIA系统中，经过量子逻辑门后量子态为、。攻击者Eve以辅助态干扰，以干扰，量子衍变过程[17]如下。

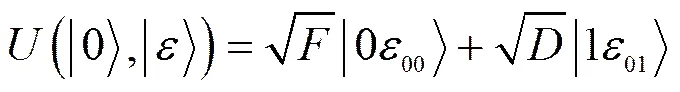
(7b)

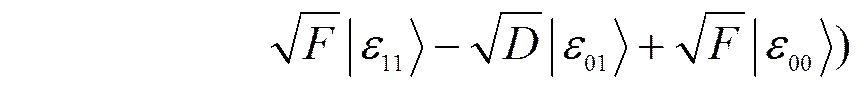
(7d)

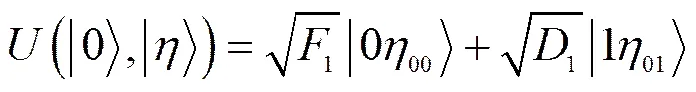
(8b)

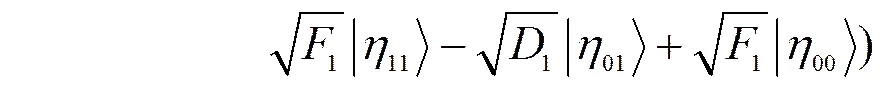
(8d)

，(9)

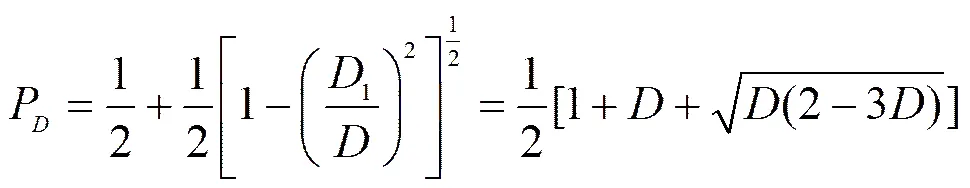
由信息论定理知，Eve可以获取信息量如式(11)所示。

(11)

图3展示了MDI-QIA框架下信息传输过程中，Eve干扰度与其获取的信息量之间的关系，当为0时，信息量为0，随着的逐渐增加，信息量与之缓慢增加，当取最大值，Eve获取的最大信息量为0.5。由于传输信道中认证信息由不同贝尔基00、01、10、11构成，在此Eve获取的概率为，以概率认定为00，则认定为01的概率为1−，由此可知，在认证密钥传输过程中Eve获得的概率如式(12)所示。

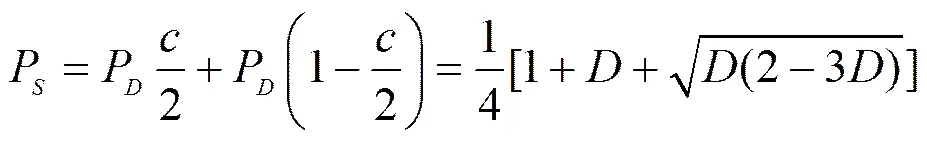
(13)

图4所示为Eve在信息传输过程中获取传输密钥的概率，定义系统身份认证密钥率为，Eve干扰度为，可以看出Eve选择不同值时，随着传输密钥率增加时，Eve获取的信息量逐渐减小，最后趋近于0，这一结果说明MDI-QIA框架中身份认证过程是安全的，随着身份认证密钥信息传输率增加，Eve获取信息量逐步减小。

3.2 MDI-QIA协议效率

Yang等[24]对于协议的比特效率定义为：，表示协议中交换的经典认证密钥总数，是协议完成认证过程需要的量子比特总数，计算经典认证密钥数量与量子比特总数即可获知协议效率。所提的MDI-QIA框架中完成认证过程所需量子比特数目为4，协议交换经典比特数为2，因此协议的效率为。

4 结束语

本文提出基于测量设备无关框架下的量子身份认证协议，借助测量设备无关协议的属性，提高了量子身份认证过程的准确性和有效性。安全性能仿真结果显示，在最强辅助纠缠攻击下，随着认证密钥传输量的增加，而Eve对认证信息的窃取量逐渐减小；且方案在本次协议认证后能自动更新共享密钥，以一次一密方式保证了身份认证过程的绝对安全性。

[1] SHOR P W, PRESKILL J. Simple proof of security of the BB84 quantum key distribution protocol[J]. Phys Rev Lett, 2000, 85: 441-446

[2] GOTTESMAN D, LO H K, LUTKENHAUS N,et alSecurity of quantum key distribution with imperfect devices[J]. Quantum Infor Comput, 2004, 4: 325-329.

[3] PAUL J, DAVID E, SÉBASTIEN K J. High bit rate continuous-variable quantum key distribution[J]. Phys Rev A, 2014, 90(4): 042329-042335.

[4] ZHOU R R, YANG L. Quantum election scheme based on anonymous quantum key distribution[J]. Chin Phys B, 2012, 21(8): 080301- 080309.

[5] ALEXANDER S, ZUREK W H. Quantum discord cannot be shared[J]. Phys Rev Let, 2013, 111(4): 040401-040406.

[6] 曾贵华. 量子保密通信[M]. 北京: 高等教育出版社, 2006. ZENG G H. Quantum private communication[M]. Beijing: Higher Educaiton Press, 2006.

[7] DUSEK M, HANDERKA O, HENDRYCH M. Quantum identification system[J]. Phys Rev A, 1999, 60(1):149-156.

[8] ZENG G H, ZHANG W P. Identity verification in quantum key distribution[J]. Phys Rev A, 2000, 61:022303-022308.

[9] 曾贵华. 不依赖于第三方的动态量子身份认证方案[J]. 电子学报, 2004, 32(7):1148-1152. ZENG G H. Quantum identity authentication without trusted-party[J]. Acta Electronica Sinca, 2004, 32(7):1148-1152.

[10] ZHOU N R, ZENG G H, ZENG W J, et al. Cross-center quantum identification based on teleportation and entanglement swapping[J]. Optics Communications, 2005, 254: 380-388.

[11] 杨宇光, 温巧燕, 朱甫臣.一种网络多用户量子认证和量子身份认证方案[J]. 物理学报, 2005, 54(9): 3995-4000. YANG Y G, WEN Q Y, ZHU F C. A theoretical scheme for multi-user quantum authentication and key distribution in a network[J]. Acta Physica Sinca, 2005, 54(9): 3995-4000.

[12] ZHANG Z S, ZENG G H, ZHOU N R, et al. Quantum identity authentication based on ping-pong technique for photons[J]. Phys Let A, 2006, 356:199-205.

[13] 张兴兰. 基于公钥的单向量子身份认证[J]. 科学通报, 2009, 59(10):1415-1418. ZHANG X L. One-way quantum identity authentication based on public key[J]. Chinese Sci Bull, 2009, 54(10):1415-1418.

[14] 李渊华, 刘俊昌, 聂义友. 基于纠缠交换和团簇态实现二粒子任意态的可控隐形传态[J]. 光子学报, 2010, 39(11):1615-1616. LI Y H, LIU J C, NIE Y Y. Controlled teleportation of an arbitrary two-particle state by using a four-qubit cluster state and entanglement swapping[J]. Acta Photonica Sinca, 2010, 39(11):1615-1616.

[15] YANG Y G, WANG H Y, JIA X. A quantum protocol for (,)-threshold identity authentication based on greenberger-horne-zeilinger states[J]. Theor Phys, 2013, 52: 524-530.

[16] HUANG P, ZHU J, LU Y, et al. Quantum identity authentication using gaussian-modulation squeezed state[J]. International Journal of Quantum Information, 2011, 9(2): 701-721.

[17] YANG Y G, TIAN J, XIA J. Quantum authenticated direct communication using bell states[J]. Theor Phys, 2013, 52: 336-344.

[18] MAKAROV V, SKAAR J. Hacking commercial quantum cryptography systems by tailored bright illumination[J]. Nature Photonics, 2010, 214(4): 686-689.

[19] ZHAO Y, FUNG C H F, QI B. Quantum hacking: experimental demonstration of time-shift attack against practical quantum-key- distribution systems[J]. Phys Rev A, 2008, 78: 042333-042340.

[20] LO H K, CURTY M, QI B. Measurement-device-independent quantum key distribution[J]. Phys Rev Let, 2012, 108: 130508-13514.

[21] TANG Z Y, LIAO Z F, XU F H, et al. Experimental demonstration of polarization encoding measurement-device-independent quantum key distribution[J]. Phys. Rev. Let, 2014, 112(19): 190503-190511.

[22] 马瑞霖. 量子密码通信[M]. 北京: 科学出版社, 2006. MA R L. Quantum cryptograghy communication[M]. Beijing: Science Press, 2006.

[23] GARCIA-PATRON R, CERF N J. Unconditional optimality of gaussian attacks against continuous-variable quantum key distribution[J]. Physical Review Letters, 2006, 97:190503-190510.

[24] YANG C W, TSAI C W, HWANG T. Fault tolerant two-step quantum secure direct communication protocol against collective noises[J]. Sci. China G:Phys. Mech. Astron,2011, 54(3):496-501.

Quantum identity authentication scheme based on measurement-device-independent quantum key distribution protocol

DONG Ying-di1,2, PENGJin-ye1,ZHANG Xiao-bo1, ZHANG Zhen-long2

(1. School of Electronics and Information, Northwestern Polytechnical University, Xi’an 710072, China; 2. School of Information and Control Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China)

Utilized to security properties ofmeasurement-device-independent quantum key distribution (MDI-QKD) protocol, quantum identityauthentication scheme based on MDI (QIA-MDI) protocol was presented. In this protocol, authentication center (AC) and authentication user have encrypted authentication information and next authenticated key by shared key, and then they transmitted the encrypted information to untrusted third party for Bell-state measurement (BSM). The secret authentication information was obtained through the BSM result, which can verify the communicator identity and update shared key. The security performance of the proposed scheme is extensively analyzed and accordingly confirmed in the case of attacks.

quantum identity authentication, quantum key distribution, measurement-device-independent, Bell-state measurement

TN911

A

10.11959/j.issn.1000-436x.2016041

2015-05-04；

2015-07-20

董颖娣，tongxindyd@126.com

董颖娣（1978-），女，陕西西安人，西北工业大学博士生，主要研究方向为量子密码通信。

彭进业（1964-），男，湖南娄底人，西北工业大学教授，主要研究方向为量子密码通信及图像处理等。

张晓博（1975-），男，陕西西安人，西北工业大学博士生，主要研究方向为模式识别与量子通信。

张振龙（1980-），男，陕西韩城人，西安建筑科技大学博士生，主要研究方向为数字图像处理。