基于图分割的流应用多处理器映射算法

唐麒，吴尚峰，施峻武，魏急波



基于图分割的流应用多处理器映射算法

唐麒，吴尚峰，施峻武，魏急波

（国防科技大学电子科学与工程学院，湖南长沙 410073）

为了充分利用多处理器平台所提供的计算资源，需要将应用以适当的方式映射到不同处理器，从而最大程度地挖掘应用所提供的并发性以满足应用严格的实时性要求。提出了并发图来量化、建模应用任务间的并发性，提出了一种基于自同步调度的并发图构建算法，并将任务映射问题转换成图分割问题，然后将并发图分割问题建模为纯0-1整数线性规划模型并采用ILP求解器获得最优解。采用了大量随机生成的同步数据流图以及一组实际应用对所提方法进行性能评估，实验结果表明所提方法性能优于已有算法。

同步数据流图；映射；多处理器；图分割

1 引言

同步数据流图（SDFG，synchronous dataflow graph）广泛用于建模现代流应用，包括视频、音频编解码、软件无线电等。为了满足消费者对应用的质量要求，这些应用的计算复杂度日益增加，给硬件设计带来了巨大挑战。许多应用有严格的实时性要求，例如，系统输入与输出间的延时或系统吞吐量要满足特定指标。为了满足这些要求，一种直接的方法是增加处理器时钟频率，然而，随着时钟频率的提升，系统能耗急剧增加，降低了这一方法的实用性。另外，时钟频率正逐渐接近物理极限，依靠这一方法增加计算能力难以为继。多处理器平台提供了另一种方案，可以在计算能力与功耗间达到更好的平衡，因此，在嵌入式系统设计中得到了大量应用。尽管多处理器可以提供很高的计算能力，这并不意味着部署在其上的应用可以完全挖掘这些处理能力。实际上，如果应用只提供了极少量的并发性，那么采用多处理器几乎不能提高系统性能。正如Amdahl定理所表明的那样，使用多处理器带来的性能增益严重受限于应用并发性。尽管很多应用，如由SDFG建模的流应用，可以并行执行，如何在多处理器上利用应用的内在并发性仍然是个有待解决的问题，这就是所谓的并行调度问题。

应用调度包括任务映射、排序和定时[2]。任务映射是将任务分配到不同处理器上的过程。对于最优调度，无论最优性的评价标准是什么，总存在对应的最优映射，因此研究如何获得最优映射具有重要价值。对于映射问题，研究者提出了很多针对不同应用模型和平台的算法。其中，图分割法[3]和负载均衡法[4,5]得到了大量研究。然而，这2类算法要么在最小化处理器间通信的前提下最大化负载均衡水平，要么单纯地均衡不同处理器上的负载，而没有综合考虑应用的内在结构，因此降低了性能。另一类方法是链式调度算法[6,7]，这类算法将任务调度分成优先级分配和调度2个步骤，然而，这类算法主要用于优化系统延时，虽然可以通过修正应用于吞吐量优化，但性能并不是很好。

本文研究SDFG在多处理器上的映射问题，以获得可以最大化应用并发性的最优任务映射，从而使应用长期吞吐量最大化。本文提出了并发图（PG，parallelism graph）来量化和建模SDFG中不同任务间的并发性，提出了一种基于自同步调度的并发图构建算法，并将映射问题转换化成图分割问题，然后将图分割问题建模为纯0-1整数线性规划模型（ILP，integer linear programming），并使用ILP求解器获取最优解。

本文所提算法在SDF3[8]中实现，并采用随机生成的SDFG和一组实际应用进行性能评估。算法的有效性通过与已有负载均衡算法[4,5]和HEFT算法[6]比较得以验证。

2 相关工作

图分割[3]被证明可以用于并行计算。图分割的主要目标是将计算均匀地分配到多个处理器，同时最小化处理器间通信[9]。然而，算法中没有考虑任务间的依赖关系。与此不同，本文提出并发图的概念，利用任务间的依赖关系，建模任务间并行执行关系，从而将问题转换成图分割问题。文献[4,5]将负载均衡思想应用于SDFG映射问题，所提算法考虑了计算、通信带宽及内存消耗的均衡，任务绑定按照优先级非递增的顺序进行，任务优先级采用估计最大均值（MCM，maximum cycle mean）[4]来计算。然而，算法没有充分利用任务间的依赖关系，不能最大化应用并发性，降低了算法性能。

文献[6,7]研究了如何利用应用结构特征，包括任务间依赖关系、任务执行时间及数据传输需求来提高调度性能。然而，这些方法针对由有向无环图（DAG，directed acyclic graph）建模的应用，不能直接应用于SDFG。与DAG不同，SDFG可以支持任务间环状依赖关系和多速率依赖，因此，任务间关系更为复杂。这种关系不能简单地由模型中的路径特征，比如路径长度来描述。一种可行的方法是将SDFG转换成同构SDFG，并进一步将同构SDFG转换为无环依赖图[2]。由于无环依赖图属于DAG，因此上面提到的调度算法可以直接使用。然而，这种方法主要用于允许任务复制的系统，为了适应无任务复制的系统，可以在调度时强制将同一任务的实例分配到同一处理器。

3 应用模型

本文采用SDFG来建模流应用，如软件无线电、通信协议、多媒体应用等。本文所采用SDFG模型的定义如下。

SDFG在执行过程中，任务将以不同频率执行，因此在一次调度中会出现不同次数。SDFG迭代及重复向量可以用于来描述SDFG的这一特征。

定义2 （SDFG迭代）SDFG迭代是执行每个任务最小正整数次数同时使各边符号数目恢复初始值的过程。

SDFG的重复向量可以通过解平衡方程而得[1]。当平衡方程有非零解[1]时，重复向量存在，且这样的 SDFG 总可以转换成等价的 HSDFG[2]。

本文只考虑强连通SDFG，其中每个任务都与其他任意任务直接或间接相连。对实际应用，这是一个合理的假定，因为实际系统内存消耗是受限的，因此SDFG中任意边的最大符号数目是有限的。通过为SDFG中的每条边增加额外的最大符号数目约束边，可以将非强连通SDFG转换成强连通图。

图1所示为一个由5个任务组成的SDFG示例。图中各边末端数字为边的产出或消费速率，为简单起见，只有当速率大于1时才予以标注。边附近的文字为边的标签，标签后面括号中的数字表示边上的初始符号数，如果初始符号数为0，则予以忽略。图中SDFG的重复向量为，表示在一次应用迭代中，任务、、、和分别需要执行2、2、3、1和次。

4 问题阐述

吞吐量是流应用最为重要的性能度量标准之一。本文研究如何将流应用映射到多处理器从而最大化应用的长期吞吐量。根据是否允许任务复制，映射问题可以分成基于复制的映射和无复制的映射。本文考虑不允许任务复制的应用映射问题，这意味着每个任务只能分配到一个处理器上执行。在本文所考虑的问题中，应用采用SDFG建模。在SDFG中，应用任务的并发执行能力并未明显建模。尽管应用的最大吞吐量可以通过自同步调度[2]获得，这一调度并未将资源约束，例如处理器数目纳入考虑之中。实际多处理器平台中处理器数目通常少于SDFG中最大可并发执行的任务数目，因此，如何在映射中尽可能地挖掘SDFG任务间并发性以提高系统吞吐量是一个极为重要的问题。

对于SDFG，尽管可以从图模型结构推导阻止任务并发执行的优先约束关系，任务间并发性并未明显地建模出来，例如，2个任务在多大程度上可以并行执行并未在应用图中得到描述。除此之外，也不能直接将任务间优先关系与任务间并行度关联起来，使在映射中挖掘任务并发性变得极为困难。尽管如此，如果可以量化任务间并发程度，则映射问题可以次优地转换成最大化任务间并发性的问题。基于以上观察，本文从提取、量化SDFG任务间并发性着手，并使用图分割法解决应用映射问题。

5 周期静态调度与吞吐量分析

由于最终目标是获得吞吐量最优的映射，分析映射的吞吐量显得极为重要。本文假定系统根据静态周期调度循环执行，静态周期调度强制任务按照指定顺序依次执行。不同迭代可以在时间上重叠，采用流水线的方式执行。本文采用最早开始时间调度算法为每个处理器构建周期静态顺序调度。当同一时刻有多个任务可以同时执行时，任意一个任务被选择优先执行。为每个处理器构建好周期静态调度后，应用吞吐量可以通过已有方法来计算。

文献[12]提出了一种无资源约束下的基于状态空间搜索的SDFG吞吐量分析方法。这一方法采用SDFG边上符号分布及任务执行状态来表征应用状态。由于所考虑SDFG是强连通的，并且状态中各元素值的范围是有限的，因此，状态空间也是有限的。经过有限次数的状态转移后，将重新遇到已经经历过的状态，从而形成状态环。获得状态空间中的状态环后，吞吐量可以直接计算出来。另一种计算吞吐量的方法是用max-plus代数[10]建模应用的自同步执行，max-plus矩阵的特征值的倒数即等于应用吞吐量。上述吞吐量计算方法没有考虑映射和调度，只适应于无资源约束的场景。文献[11,13]提出了将周期静态顺序调度建模到HSDFG/SDFG中的方法，通过对SDFG进行调度扩展，可以用文献[10,12]中的吞吐量分析方法进行精确的吞吐量分析。本文使用文献[11,12]中的方法进行调度性能分析。

6 并发图及其构建

本节介绍并发图的概念及其构建方法。并发图用于量化和建模SDFG任务间的并发性，其定义如下。

本文通过SDFG的ASAP（as-soon-as-possible）调度（自同步调度[2]）的周期扩展来计算任务间并发度。在ASAP调度中，当任务所依赖数据就序时，任务即开始执行。ASAP调度定义如下。

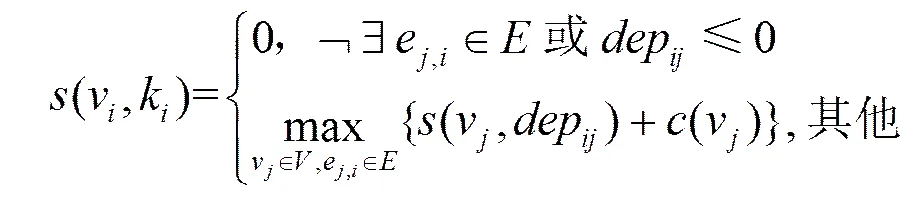
ASAP调度由瞬态和紧随其后的周期态组成，其定义如下。

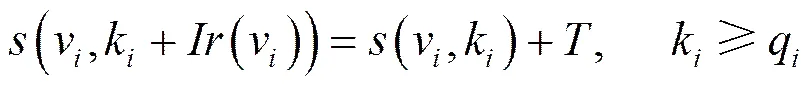
应用吞吐量由ASAP调度的周期态决定，因此使用它来计算任务间并发度。尽管周期态中一个周期可能包含多次应用迭代，如周期态定义中的所指明的那样，无论最后计算出的任务间并发度是否除以这一数值，并不会影响最后结果。由于周期态具有周期特征，因此并不需要构建完整的ASAP调度，可以在获得一个完整的执行周期后停止执行。本文从周期态中提取一个执行周期，对其进行周期扩展，并根据这个周期扩展中不同任务的并行执行时间来量化任务间并发度。

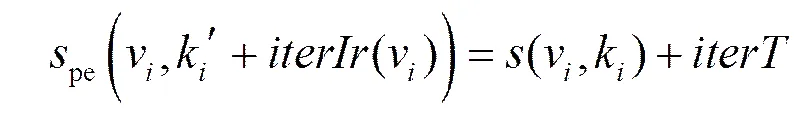
图1所示SDFG的ASAP调度如图2所示，ASAP调度由瞬态和周期态组成。周期态从时刻18开始；在时刻53，再次经历时刻18经历的状态。因此时刻18和53之间的执行形成一个周期，其中包含一次应用迭代。

并发图构建算法详细描述了构建并发图的步骤。对一个SDFG，首先为其增加自边以约束任务自动并发，也即同一时间一个任务最多只能有一个实例处于运行状态。然后，初始化并发图，为其添加节点。并发图中的每个节点对应SDFG中的一个任务。其次，反复调用方程(1)构建SDFG的ASAP调度。在此过程中，提取ASAP调度的一个执行周期，并对其进行周期扩展。根据得到的周期扩展，计算PG中任意2个节点间的边权，边权等于对应任务在周期扩展中的重叠时间。

并发图构建算法

11) end for

15) end if

16) end for

STEM教育与STEM职业的联系 教育的目的是为社会建设培养专业人才，对接社会的现代化发展。STEM教育理工科属性很强，从事社会建设的科技产业建设者需要具有此类的设计性思维，对于社会的科技产业具有很强的带动作用。

17) end for

如算法中第6)~17)行所示，并发图中2个节点间边的边权通过累加对应任务实例的并行执行时间而得。如果计算得到的边权非零，则在并发图中为相应节点增加一条边，边权设置为上面计算得到的值。

图3为示例SDFG的并发图及其邻接矩阵。如图2所示，不同执行周期在时间上不重叠，例如，第1个周期开始于时刻18而结束于时刻53，第2个周期开始于时刻53而结束于时刻87。因此，构建并发图时，并不需要进行周期扩展。在图2所示ASAP调度的第一个周期中，任务实例（上标表示实例索引）与重叠，重叠时间为5，因此，在并发图中，任务和间有一条边，边权为5。类似地，可以为并发图添加其他边。

在并发图中，由于边权均为正整数，因此每一条边均表示该边所连接任务在一定程度上可以并发执行，边权记录了对应任务可并发执行的程度。如果在调度中有尽可能多的任务可以并发执行，则应用的一次迭代可以在更少的时间内完成，因而提高应用吞吐量。因此，以最大化吞吐量为目标的映射问题，在一定程度上可以等价于最大化映射的并发度。通过使用并发图，任务间并发性得以量化，映射问题可以等价于分割并发图并使割最大化。割定义为所连接任务被分配到不同处理器的边的边权之和。采用上述方法，可以将映射问题转化成图分割问题。

7 纯0-1整数线性规划模型

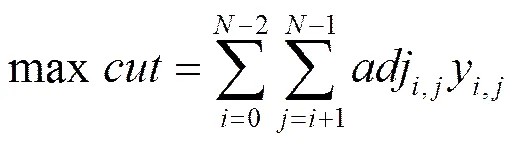
(4)

(5)

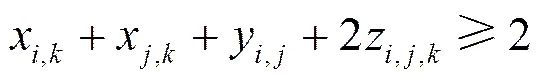
(7)

(8)

由于每个任务只能映射到一个处理器，因此必须满足如式(4)所示的任务映射约束。由于引入了辅助变量使如式(3)所示目标函数线性化，需要引入约束式(4)~式(8)。这些约束方程的推导如下。

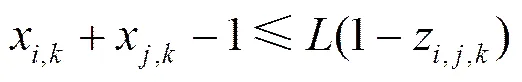
(10)

(11)

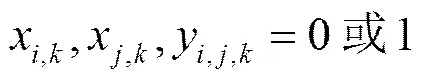
8 实验与结果

本节通过实验来评估所提算法的性能，并将本文所提算法与负载均衡算法[4]及HEFT算法[6]进行了比较。

8.1 度量参数

吞吐量是流应用系统的关键优化目标，如同文献[4,5]一样，本文采用吞吐量对算法性能进行评估。吞吐量采用第5节所介绍的方法计算。同时，在实验中分析了不同映射算法所获得映射方案的割值及算法时间开销。割值大小反映了映射所挖掘的并发度，定义为跨越不同子集的边的边权之和。

8.2 测试基准

本文使用一组随机生成的SDFG及一组实际应用进行性能测试，并使用开源工具SDF3[8]来产生随机SDFG，其中任务数为5到15。对每个图尺寸，均生成个100个随机SDFG。SDFG参数包括任务执行时间和边上的符号大小，均随机生成。任务累积执行时间在400和1 000间均匀产生。

8.3 实验结果

表1所示为随机应用在具有不同处理器数目的多处理器上的测试结果。表中第1列和第2列分别表示随机SDFG的任务数目和平台处理器数目。“吞吐量”、“割值”、“时间复杂度”列中所有数值均进行了归一化。从表中可以看出，对不同多处理器和有不同任务数的SDFG，本文所提算法从吞吐量的角度看要优于其他2种算法，吞吐量平均增加17.40%和18.23%。这一性能增益表明最大化并发度的思想有助于提升映射的吞吐量。由于采用并发图来表示应用并发性，并采用图分割方法最大化映射的割值，采用本文所提算法所获得的映射在并发度的数值上要大于负载均衡算法和HEFT。如“割值”列中数据所示，在所有测试中，所提出的算法所生成的映射的割值比负载均衡算法大10%，比HEFT高21.95%。采用本文所提算法的时间复杂度高于其他2种算法。当任务数目较小的，时间复杂度是负载均衡算法的数倍；而当任务数较大时，复杂度急剧增加，这表明所提算法可较好地应用于小规模问题。

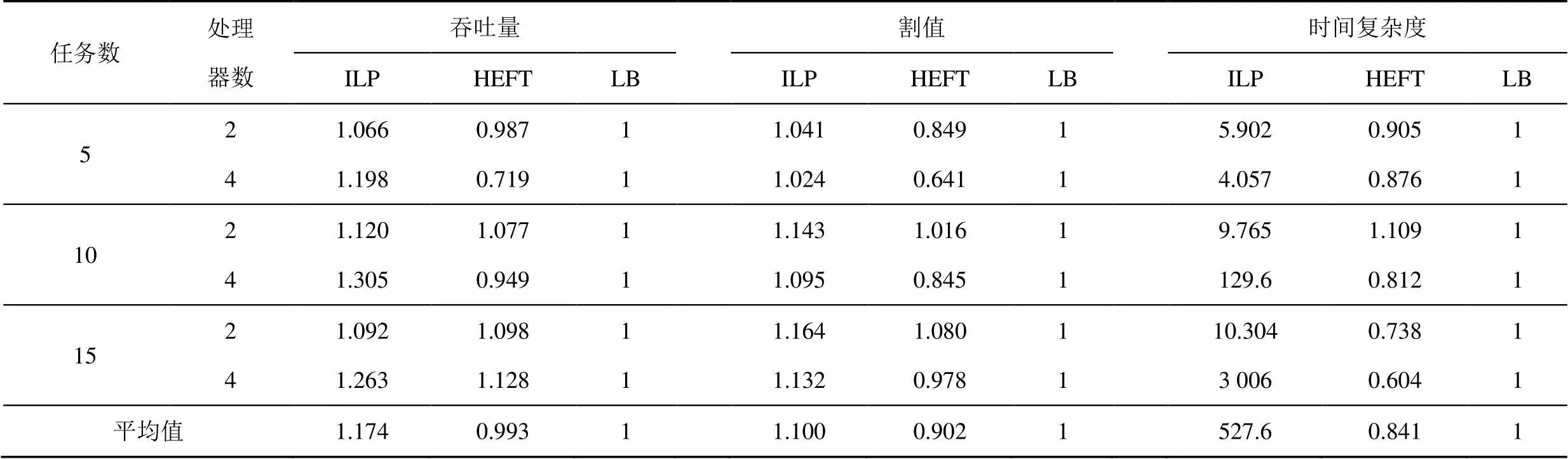
表1 随机应用性能对比

表2所示为实际应用在多处理器上的测试结果。表中数据表明本文所提算法对实际应用仍然有效，吞吐量要优于负载均衡算法和HEFT。对调制解调器，使用所提算法与负载均衡算法和HEFT相比可以提高9.6%和18.6%的吞吐量。对其他应用，也可取得一定的性能增益。与随机应用一样，使用本文算法可以提高映射割值，再次验证了映射割值与吞吐量之间的正相关关系，表明采用割值来优化映射问题要优于其他方法。在时间复杂度方面，除MP3解码器1外，所提算法与负载均衡算法相当，略高于HEFT，表明所提算法可较好地应用于实际应用。

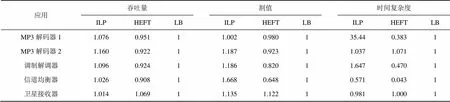
表2 实际应用性能对比

9 结束语

本文研究了SDFG在多处理器上的映射问题，以最大化应用吞吐量为目标。提出了并发图来量化、建模应用并发性，提出了一种基于自同步调度的并发图构建算法，并将映射问题转换为图分割问题，最后将图分割问题建模为纯0-1整数线性规划问题。本文采用了一组实际应用和随机产生的SDFG进行了算法性能评估。实验结果表明本文所提算法的吞吐量性能要优于负载均衡算法和HEFT算法，证明采用并发图及图分割的方法求解映射问题优于已有方法。

[1] LEE E A, MESSERSCHMITT D G. Static scheduling of synchronous data flow programs for digital signal processing[J]. IEEE Transactions on Computers, 1987, 100(1): 24-35.

[2] SRIRAM S, BHATTACHARYYA S S. Embedded multiprocessors: scheduling and synchronization[M]. CRC Press, 2012.

[3] AUBANEL E. Resource-aware load balancing of parallel applications[M]// Handbook of research on grid technologies and utility computing: concepts for managing large-scale applications. 2009: 12-21.

[4] STUIJK S, BASTEN T, GEILEN M, et al. Multiprocessor resource allocation for throughput-constrained synchronous dataflow graphs[C]// The 44th Annual Design Automation Conference. c2007: 777-782.

[5] AMBROSE J A, NAWINNE I, PARAMESWARAN S. Latency- constrained binding of dataflow graphs to energy conscious GALS- based MPSoCs[C]//IEEE International Symposium on Circuits and System. c2013: 1212-1215.

[6] TOPCUOGLU H, HARIRI S, WU M. Performance-effective and low-complexity task scheduling for heterogeneous computing[J]. IEEE Transactions on Parallel and Distributed Systems, 2002, 13 (3): 260-274.

[7] SINNEN O. Task scheduling for parallel systems[M]. John Wiley & Sons, 2007.

[8] STUIJK S, GEILEN M, BASTEN T. SDF3: SDF for free[C]// Conference on Application of Concurrency to System Design. c2006: 276-278.

[9] HENDRICKSON B, KOLDA T G. Graph partitioning models for parallel computing[J]. Parallel Computing, 2000, 26 (12): 1519-1534.

[10] GEILEN M. Synchronous dataflow scenarios[J]. ACM Transactions on Embedded Computing Systems, 2010, 10 (2): 16.

[11] DAMAVANDPEYMA M, STUIJK S, BASTEN T, et al. Schedule-extended synchronous dataflow graphs[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2013, 32 (10): 1495-1508.

[12] GHAMARIAN A H, GEILEN M, STUIJK S, et al. Throughput analysis of synchronous data flow graphs[C]//Sixth International Conference on Application of Concurrency to System Design. c2006: 25-36.

[13] BAMBHA N, KIANZAD V, KHANDELIA M, et al. Intermediate representations for design automation of multiprocessor DSP systems[J]. Design Automation for Embedded Systems, 2002, 7 (4): 307-323.

[14] WINSTON W L, GOLDBERG J B. Operations research: applications and algorithms[M]. Duxbury Press, 2004.

Graph partition based mapping algorithm on multiprocessors for streaming applications

TANG Qi, WU Shang-feng, SHI Jun-wu, WEI Ji-bo

(College of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China）

To take advantage of multiprocessor platform, it is a necessity to map tasks of the application properly onto different processors to exploit the concurrency in the application and thus meet the stringent timing requirements. Parallelism graph was proposed to quantify and model the concurrency among tasks of the application. An algorithm was also proposed to construct the parallelism graph based on the self-timed schedule and transform the mapping problem to a graph partitioning problem. The graph partitioning problem as a pure 0-1 integer linear programming model was further formulated and the ILP solver to find the optimal result. A lot of randomly generated synchronous dataflow graphs and a set of practical applications were used to evaluate the performance of the proposed method. The experimental results demonstrate that the proposed method outperforms available algorithms.

synchronous dataflow graph, mapping, multiprocessor, graph partition

TP399

A

10.11959/j.issn.1000-436x.2016123

2015-10-14；

2016-05-11

国家自然科学基金资助项目（No.61471376）

The National Natural Science Foundation of China (No.61471376)

唐麒（1986-），男，湖南益阳人，国防科技大学博士生，主要研究方向为软件无线电技术和嵌入式并行计算。

吴尚峰（1986-），男，重庆人，国防科技大学博士生，主要研究方向为软件无线电技术。

施峻武（1977-），男，云南曲靖人，国防科技大学讲师，主要研究方向为软件无线电技术。

魏急波（1967-），男，湖南汉川人，国防科技大学教授、博士生导师，主要研究方向为通信信号处理与通信网络。