基于MATLAB的不校正自差的磁罗经使用研究

樊明波 蔡 君 高 杨

（镇江船艇学院 镇江212003）



基于MATLAB的不校正自差的磁罗经使用研究

樊明波 蔡 君 高 杨

（镇江船艇学院 镇江212003）

［摘 要］磁罗经是船舶必备的导航仪器，由于船磁的影响，要使用磁罗经需要先校正磁罗经自差。为达到不校正自差而使用磁罗经，通过采集船舶转向一周里部分罗航向对应的自差，根据磁罗经自差基本公式建立方程组，利用MATLAB软件求得自差系数。然后把自差系数代入自差基本公式求解出任意航向上的自差。结果表明，利用自差基本公式求解出的航向自差与在该航向上进行的实测自差在1°以内，能够很好地代替实测自差来使用磁罗经。

［关键词］磁罗经;罗航向;自差;自差公式

引 言

随着工业的巨大发展，船舶制造逐步由钢铁代替木材，同时配备了各种先进的导航仪器，其中主要的指向设备是根据陀螺原理设计的陀螺罗经和感应地磁力设计的磁罗经。磁罗经作为传统的指向设备由指南针演变过来，简单可靠且不需要任何能源，被国际海事组织（IMO）确定为必须安装的设备。但是磁罗经最大的缺点是受到船磁影响产生自差，并且这种自差还会随着航行纬度和时间的变化而变化。这就要求船舶在跨纬度海域航行时重新校正磁罗经，而且必须每年校正［1］。

对于磁罗经自差的消除方法普遍认可的是英国天文学家爱利提出的爱利法，通过消除各自差力产生的最大自差角来消除各自差力［2］。在此基础上也延伸出很多方法，诸如人为航向法［3］、船靠码头法［4］、数字化校正法［5］等。这些方法都旨在消除磁罗经自差。在消除磁罗经自差的过程中费时费力，以爱利法为例，不仅需要船舶航行到磁罗经自差校正水域，还需要在该水域进行4个主点和2个隅点的一段时间的保向航行，磁罗经校正人员在那段时间里通过添加和移动磁棒和软铁片来消除磁罗经自差。本文以磁罗经自差基本公式为基础，在一个周期内采集若干航向的自差，选取部分航向利用MATLAB编程得到自差系数，然后反推各个航向的自差。

1　磁罗经自差基本公式

船舶上的磁罗经受到地磁力、硬铁磁力和软铁磁力的共同作用而产生自差，自差δ与罗航向CC的函数关系可由式（1）的傅里叶级数展开式近似表示：

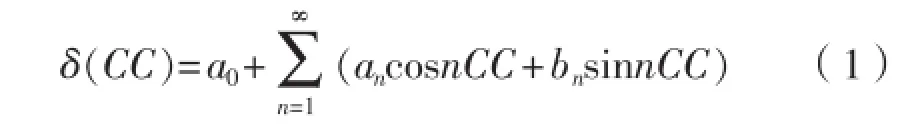
这就是磁罗经自差的基本公式，式中罗航向CC的定义域为［0°，360°］。如果取不同的罗航向CC，就有不同的自差δ（CC）。当船舶磁罗经的罗航向为CC0、CC1、… CCm时，磁罗经的自差为δ0、δ1、… δm，可以得到如式（2）方程组。

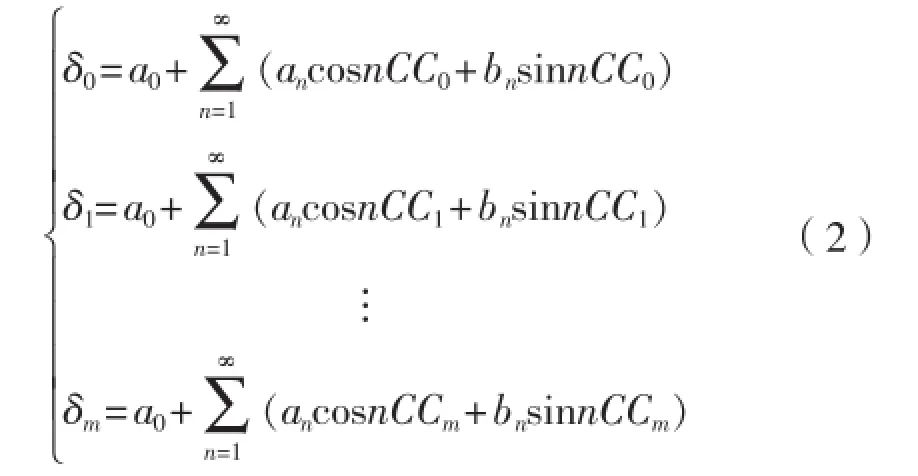
把方程组转化成如式（3）的矩阵形式。

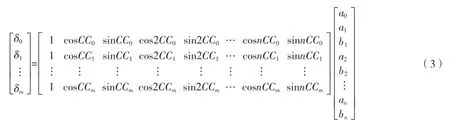
假设矩阵形式中的自差矩阵为b，需要测量的罗航向正余弦矩阵为A，自差系数矩阵为x，则该矩阵可以写为b = Ax。需要求解的是自差系数矩阵x，对于大量的数字矩阵运算，可以利用数学编程软件MATLAB编程，计算x = A/b得到。

理论上项数n可取无穷次，当项数n取无穷次时，该函数完全能描述出自差与罗航向的关系。但在实际中，n取一个有限数值，该数值的大小是由校差的精度要求来决定的［6］。在磁罗经校正工作完成后，再次让船舶航行在8个航向上（4个主点和4个隅点）测得各自的自差。然后对磁罗经自差基本公式取前5项，由8个航向上的自差得到8个方程组，应用最小二乘法求解得到这前5项的系数。最后把这5个系数代入到磁罗经自差基本公式中求解任意航向上的自差［1］。

在磁罗经自差基本公式的处理上，公认是只选取前5项，而且是在磁罗经自差校正工作完成之后进行，这样求得的自差是不精确的。假如1个磁罗经没有进行自差校正，从磁罗经自差基本公式中可以看出，选取的项数越多，求解出来的自差系数也就越多，带入到自差基本公式中求解任意航向上的自差也就越精确。

2　数据采集分析

依据磁罗经自差基本公式，在船舶转向一周里采集各个罗航向和航向对应的自差。然后从采集的航向和自差数据中取出部分数据进行MATLAB编程，得到自差系数。最后把自差系数代入到自差基本公式中求解采集航向数据中的其他航向所对应的自差，比较得出实际采集和编程计算的差距。

2.1数据采集

数据采集是在两艘未校正磁罗经自差的船上进行的，给两艘船编号为1和2，其中，船2的磁罗经相较于船1的磁罗经自差大很多。把两艘船开到开阔海域，分别按照各自磁罗经的罗航向航行，让船转向一周，每隔5°进行一次数据采集，包括磁罗经的罗航向和通过电罗经比对得到的自差，两艘船磁罗经自差随罗航向的变化如图1所示。

从图1可以看出，随着罗航向的变化，两艘船的磁罗经自差曲线由于人为的读数误差，虽然有不平滑的地方，但大致是按照正余弦趋势变化的，符合自差基本公式。而且船2的磁罗经自差远大于船1的磁罗经自差。

2.2数据分析

由于磁罗经的自差变化周期是360°，所以从自差数据（实测自差）中选取的数据应尽可能地反映自差的变化趋势，也就是说要在各个象限里都有取值。从罗航向的0°开始，每隔一定度数选取一个罗航向。根据选取的罗航向个数确定自差公式中的自差系数个数，然后建立方程组，解出自差系数。最后把自差系数和采集的所有罗航向数据代入自差基本公式中，求解出采集的所有罗航向对应的自差（计算自差），与实测自差进行比对。

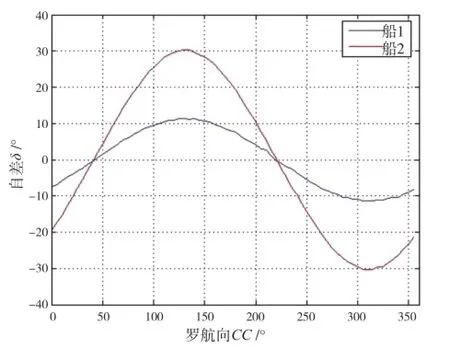
图1　自差曲线图

（1）图2为两艘船从罗航向的0°开始，每60°选取一个罗航向的自差比对图。从图中可以看出，计算自差和实测自差相差不大，船1的最大相差0.602 2°，在航向220°位置；船2的最大相差0.725 9°，在航向215°位置。

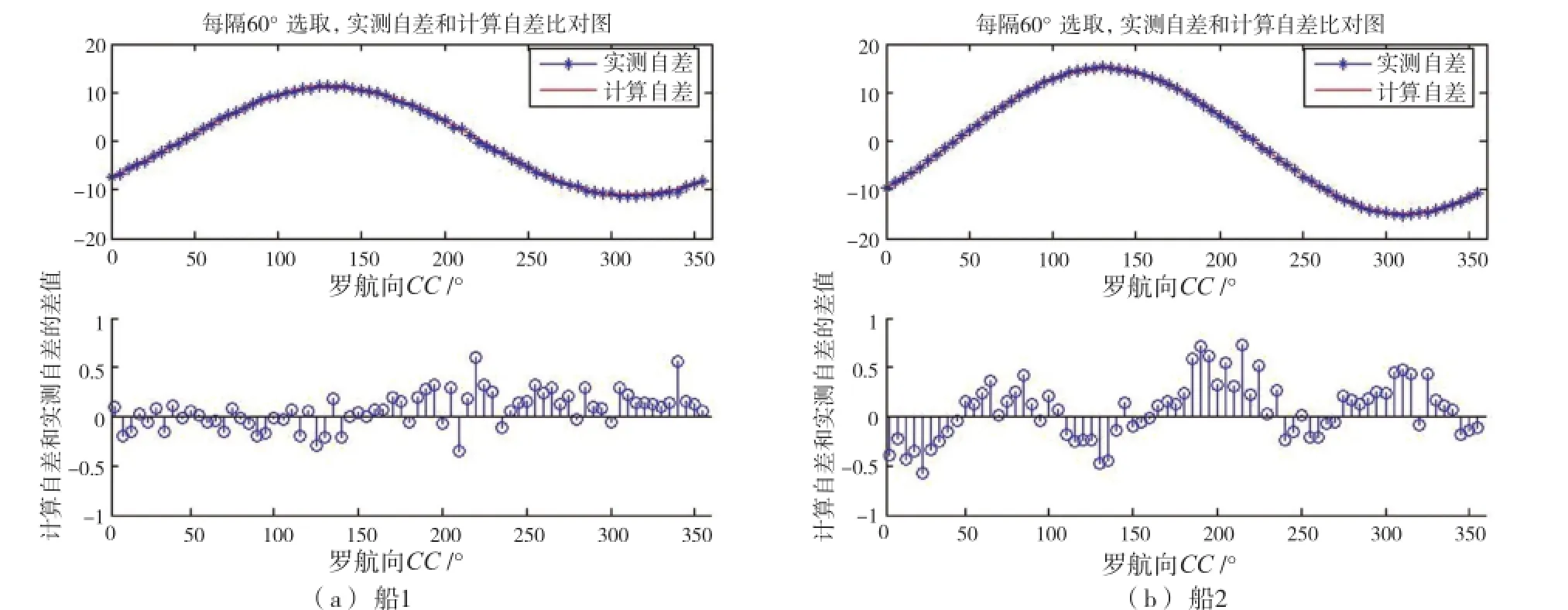
图2　每隔60°自差比对图

（2）图3为两艘船从罗航向的0°开始，每45°选取一个罗航向的自差比对图。从图中可以看出，计算自差和实测自差也相差不大，船1的最大相差-0.505 0°，在航向220°位置；船2的最大相差0.601 5°，在航向145°位置。相较于每隔60°选取一个数据进行计算，每隔45°选取的数据更能反映磁罗经自差的变化趋势，而且也考虑到4个主点和4个隅点方向的影响，所以实测自差和计算自差的差距更小。

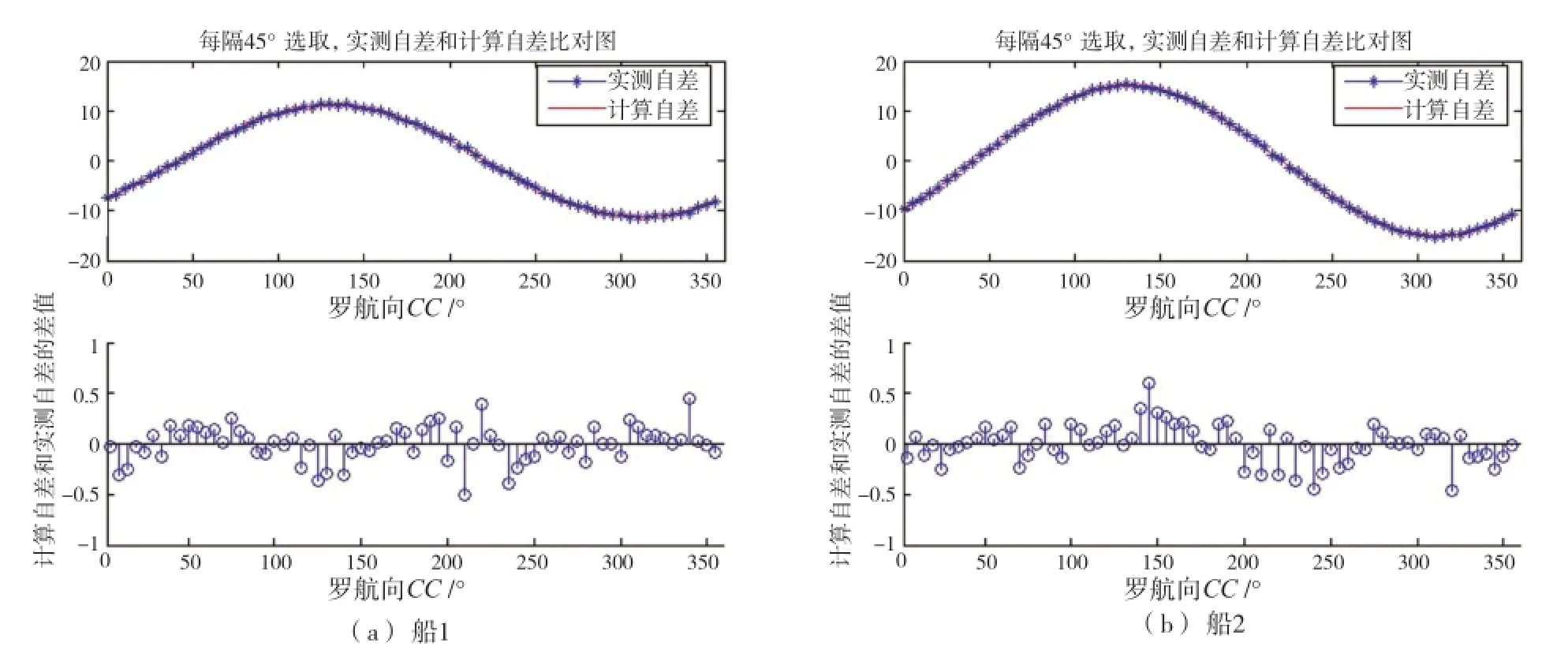
图3　每隔45°自差比对图

（3）图4为两艘船从罗航向的0°开始，每40°选取一个罗航向的自差比对图。从图中可以看出，计算自差和实测自差相差不大（船1的最大相差0.758 8°，在航向340°位置；船2的最大相差1.533°，在航向325°位置）。相较于每隔45°选取一个数据进行计算，每隔40°选取数据虽然量增大了，但由于忽略了隅点方向的自差，因此实测自差和计算自差的差距变大了。此外，相较于60°取一个数据进行计算，每隔40°选取的数据虽然量也大了，但由于忽略了南向的自差，因此实测自差和计算自差的差距变大了。

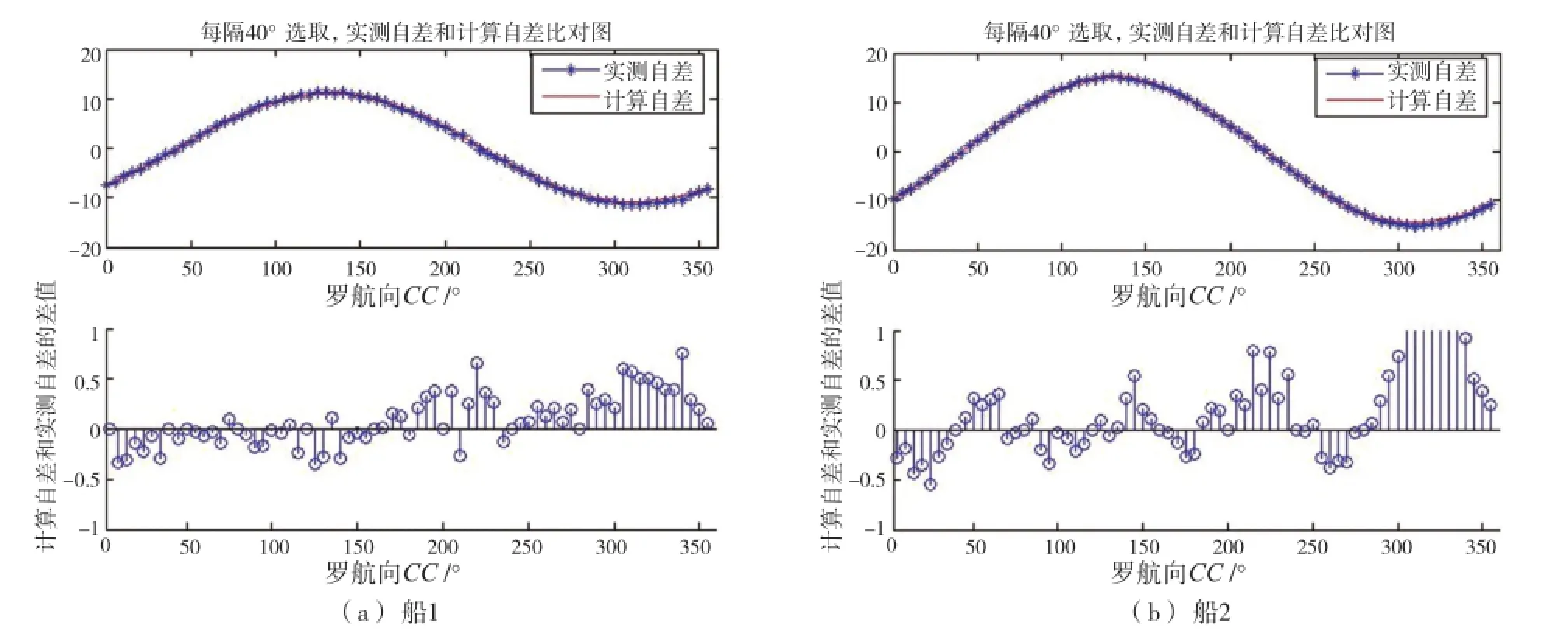
图4　每隔40°自差比对图

（4）为考虑到4个主点和4个隅点对自差的影响，以及获得更多的自差系数，从罗航向的0°开始，每15°选取一个罗航向进行自差比对计算，结果如图5所示。从图中可以看出，计算自差和实测自差相差不大，船1的最大相差0.549 8°，在航向220°位置；船2的最大相差-0.506 0°，在航向320°位置。总体而言实测自差和计算自差从一定程度上减小了，计算出来的自差更能代表实测自差。由于存在人为读数误差，造成船1的最大相差0.549 8°比每隔45°选取一个数据进行计算的结果-0.505 0°大。

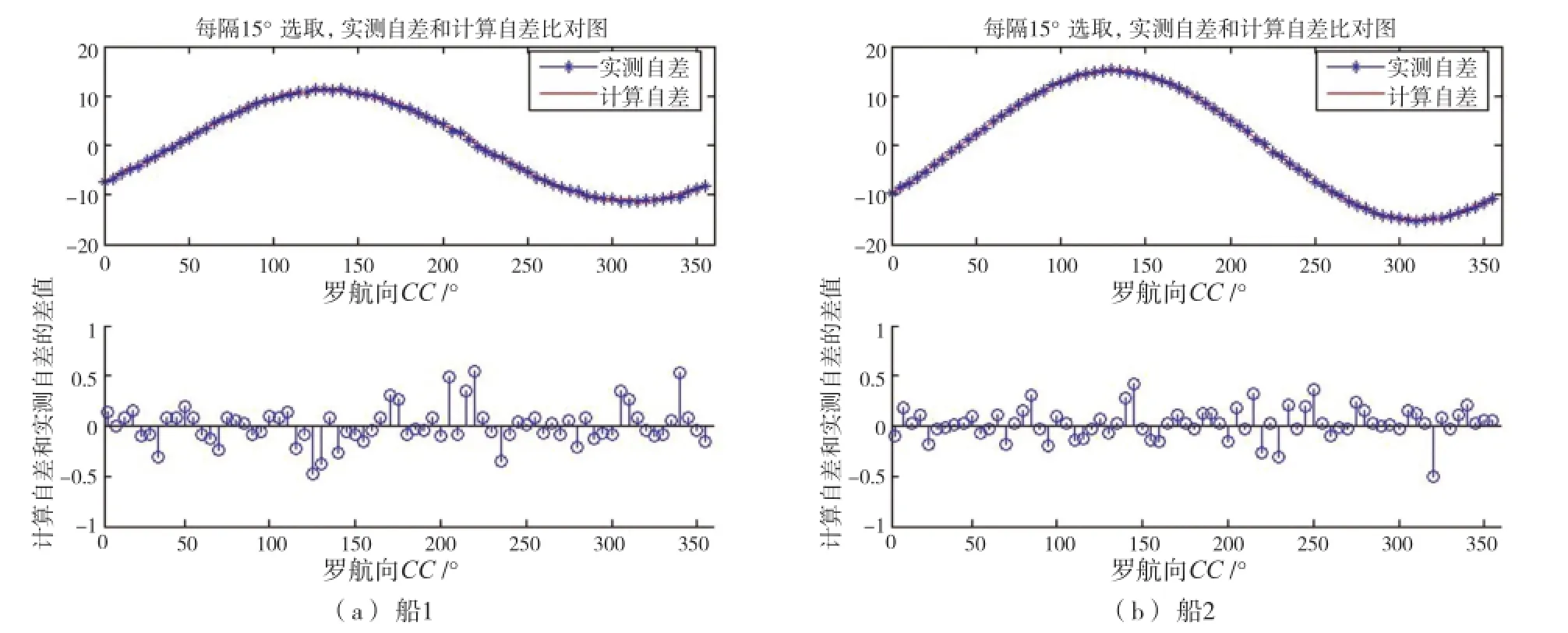
图5　每隔15° 对图

3　结 论

通过采集部分航向上的自差数据，利用磁罗经自差基本公式组成方程组，计算自差系数；然后把自差系数代入磁罗经自差基本公式中，就可以计算出任意罗航向上的自差。通过MATLAB计算分析结果表明，用于计算自差系数的数据越多，得到的计算自差越能代表实测自差；同等条件下，在用于计算自差系数的数据中，应尽可能包含4个主点和4个隅点航向上的自差。

［参考文献］

［1］ 关政军.航海仪器［M］.大连：大连海事大学出版社，2009：72-78.

［2］ 赵柯，时昌金，王则胜.利用卫星定位实现对爱利法消除磁罗经自差的改进［J］.船海工程，2009（6）：139-141.

［3］ 谢世平.船舶消除磁罗经自差的“人为航向法”［J］.武汉船舶职业技术学院学报，2008（6）：27-30.

［4］ 关政军.船靠码头校正磁罗经自差［J］.大连海事大学学报，2000（3）：39-42.

［5］ 季本山.磁罗经自差的数字化校正法［J］.航海技术，2009（6）：32-35.

［6］ 李博.基于三角函数系的磁罗经自差校正方程［J］.青岛大学学报（自然科学版），2002（4）：124-126.

Magnetic compass application without self-deviation adjustment based on MATLAB

FAN Ming-bo CAI Jun GAO Yang
(Zhenjiang Watercraft College, Zhenjiang 212003, China)

Abstract:As a necessary navigation instrument on a ship, magnetic compass needs to be adjusted before the application due to the magnetic force on the earth. In order to use the magnetic compass without adjustment, this paper firstly collects the partial self-deviations corresponding to the compass course during the ship turns round in a circle. The self-deviation coefficients are obtained with MATLAB by solving a set of equations based on the basic self-deviation formula of the magnetic compass. The self-deviation coefficients are then substituted into the basic formula to get the self-deviations on any compass course. The results show that the difference between the self-deviations solved by the basic formula and the measured self-deviations are within one degree. Therefore, the solved self-deviations can be used on the magnetic compass instead of the measured ones.

Keywords:magnetic compass, compass course, self-deviation, self-deviation formula

［中图分类号］U666.15

［文献标志码］A

［文章编号］1001-9855（2016）02-0072-05

［收稿日期］2015-09-07；［修回日期］2015-10-28

［作者简介］樊明波（1986-），男，研究生，助教，研究方向：航海仪器故障诊断技术。蔡 君（1988-），男，研究生，助教，研究方向：航海仪器故障诊断技术。高 杨（1987-），男，研究生，讲师，研究方向：船舶避碰技术。