改进的无单元Galerkin方法在机场复合道面中的应用

彭妙娟+席伟成

摘要：运用改进的无单元Galerkin（Improved Element-Free Galerkin，IEFG）方法计算机场复合道面的位移和应力，分析不同的节点数量和影响域比例参数对计算结果的影响.结果表明：节点数在4 000以上、影响域比例参数取2.5～3.5时计算结果较好；IEFG方法比无单元Galerkin（Element-Free Galerkin，EFG）方法的精度更高，计算速度更快.计算结果可为机场道面设计提供参考.

关键词：改进的移动最小二乘法； 改进的无单元Galerkin方法； 机场复合道面； 节点数； 比例参数； 位移； 应力

中图分类号： U416.217

文献标志码： B

Abstract：The displacement and stress of composite airfield pavement are obtained using Improved Element-Free Galerkin（IEFG） method， and the effect of different node number and proportion parameter of influence domain on calculation results is analyzed. The results show that， the calculation results are good when the number of nodes is more than 4 000 and the proportion parameter of influence domain is 2.5～3.5； the IEFG has higher calculation accuracy and efficiency than the Element-Free Galerkin（EFG） method. The calculation results can be referenced when the airfield pavements are designed.

Key words：improved moving least-squares approximation； improved element-free Galerkin method； composite airfield pavement； node number； proportion parameter； displacement； stress

0 引 言

无网格方法的研究已经有近20年的历史.国际上将基于点的近似、不需要在求解域内划分用于确定插值函数的网格的方法称为无网格方法.[1-2]

无单元Galerkin方法（Element-Free Galerkin，EFG）是目前最重要且应用最为广泛的无网格方法之一.[3-4]EFG方法采用移动最小二乘法建立逼近函数，相对于有限元法来说计算量较大.

程玉民等在移动最小二乘法的基础上，建立改进的移动最小二乘法和复变量移动最小二乘法.[5-9]在此基础上发展出改进的无单元Galerkin（Improved Element-Free Galerkin，IEFG）方法[10-16]、边界无单元方法[17-20]、复变量无单元Galerkin方法[21-27]和改进的复变量无单元Galerkin方法[28-32]等.

由于改进的移动最小二乘法形成的方程组易于求解且不会形成病态方程组，因而IEFG方法比EFG方法具有更高的计算精度和计算效率.

目前，国内外对机场复合道面的数值模拟大多采用有限元法，使用无网格方法对机场复合道面进行力学分析的研究较少.马翔等[33-34]基于Abaqus使用正交设计法对复合式机场道面载荷应力进行分析，林小平[35]使用有限元法对复杂条件下机场跑道模型进行分析，提出沥青加铺层的结构设计理论与方法.

本文建立机场复合道面模型，基于IEFG方法对半刚性沥青路面和复合机场道面模型的位移和应力进行计算，分析不同节点布置以及不同的影响域比例参数对计算结果的影响.

1 改进的移动最小二乘法

3 IEFG方法在机场复合道面工程中的应用

使用IEFG方法对5层结构的机场复合道面二维模型进行简化计算，分别使用布置一定节点数改变影响域比例参数dmax和固定影响域比例参数改变节点数这2种方法，验证适合计算模型的节点数和dmax值.该方法为机场复合道面的计算提供一种新的思路.

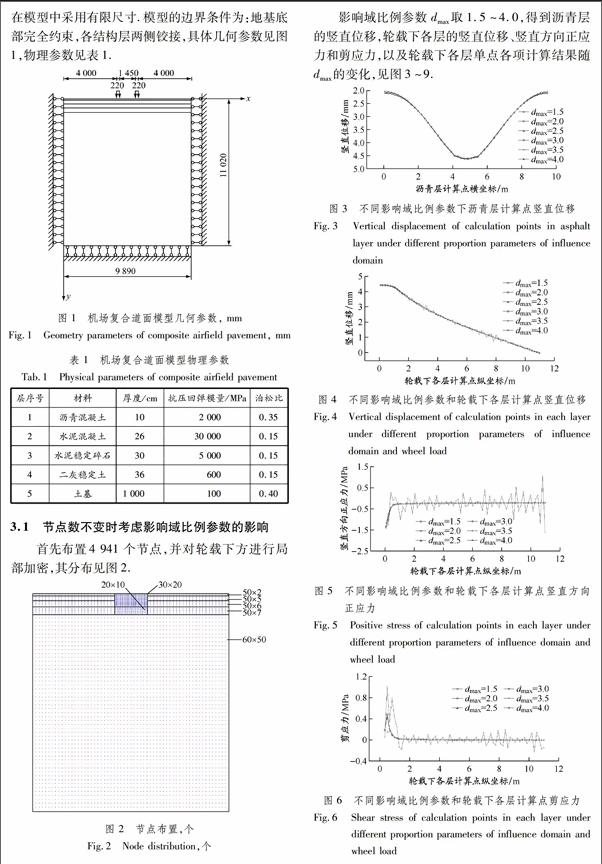
将载荷简化为二维平面应变问题下的条形均布载荷，采用B777-200B机型，轮压为1.45 MPa，轮距为1.40 m.此外，假定各结构层都由线弹性的各向同性、均质材料组成，地基由弹性半空间地基假设，在模型中采用有限尺寸.模型的边界条件为：地基底部完全约束，各结构层两侧铰接，具体几何参数见图1，物理参数见表1.

3.1 节点数不变时考虑影响域比例参数的影响

首先布置4 941个节点，并对轮载下方进行局部加密，其分布见图2.

影响域比例参数dmax取1.5～4.0，得到沥青层的竖直位移，轮载下各层的竖直位移、竖直方向正应力和剪应力，以及轮载下各层单点各项计算结果随dmax的变化，见图3～9.

3.2 影响域比例参数不变时考虑节点数的影响

取影响域比例参数dmax=3.5，节点分布仍采用轮载下加密并改变节点数目分别为1 986，3 045，4 000，4 941和6 006，计算结果见图10～16.

3.3 考虑水泥混凝土层板块接缝的计算模型

在上述模型的基础上，考虑水泥混凝土板块间的接缝，使用弹性模量E=2×105 MPa的拉杆以及E=40 MPa的填缝料，泊松比均为0.3.对接缝材料进行节点加密，其局部放大见图17.计算沥青层竖 直位移，见图18.

3.4 计算结果分析

将影响域比例参数dmax=3.5和节点个数为4 941的模型计算结果与Abaqus有限元结果进行对比，见图19.

由图19可以看出IEFG方法和有限元

法的计算结果基本一致.

综上所述：机场复合道面的计算模型中影响域比例参数取值范围应当为2.5～3.5，过大或过小都会对计算结果有明显的影响；当节点数超过4 000以后，随着节点的增加计算结果也更趋于稳定，在保证计算精度的同时选择适当的节点数目以提高计算效率是有必要的.

此外，在外载荷一定的情况下：竖直位移主要发生在道面的表面层；在假定各结构层完全连续由线弹性的各向同性、均质材料组成，且地基由弹性半空间地基假设时，在竖直方向的最大正应力主要在沥青混凝土层中，而最大剪应力在水泥混凝土层中.

4 结 论

1）运用IEFG方法计算机场复合道面模型，并与有限元计算结果进行对比，证明无网格方法在计算这类工程问题中的有效性.

2）通过运用IEFG方法对半刚性基层沥青路面模型进行计算，表明改进的移动最小二乘法选取正交作为基函数，比传统移动最小二乘法形成的无网格方法计算速度更快，在满足同样精度的条件下所需选取的节点数目更少.

3）通过数值分析，得到复合机场道面计算模型中合适的节点数目和影响域比例参数的选择范围.在保证计算精度的同时应该选取较少节点以提高计算效率.影响域比例参数过大或过小对计算结果均有不利影响，在数值计算中需要通过多次试算来确定其范围.

4）数值计算结果表明：在外载荷一定的情况下，竖直位移主要发生在道面的表面层；在竖直方向的最大正应力主要在沥青混凝土层，最大剪应力在水泥混凝土层中.

参考文献：

[1] CHENG Y M， WANG W Q， PENG M J， et al. Mathematical aspects of meshless methods[J]. Mathematical Problems in Engineering， 2014（1）： 756297.

[2] CHENG R J， CHENG Y M. Error estimate for the finite point method[J]. Applied Numerical Mathematics， 2008， 58（6）： 884-898.

[3] BELYTSCHKO T， LU Y Y， GU L. Element-free Galerkin methods[J]. International Journal for Numerical Methods in Engineering， 1994， 37（2）： 229- 256.

[4] 程荣军， 程玉民. 势问题的无单元Galerkin方法的误差估计[J]. 物理学报， 2008， 57（10）： 6037-6046.

CHENG R J， CHENG Y M. Error estimates of element-free Galerkin method for potential problems[J]. Acta Physica Sinica， 2008， 57（10）： 6037-6046.

[5] 程玉民， 陈美娟. 弹性力学的一种边界无单元法[J]. 力学学报， 2003， 35（2）： 181-186.

CHENG Y M， CHEN M J. A boundary element-free method for linear elasticity[J]. Acta Mechanica Sinica， 2003， 35（2）： 181-186.

[6] 陈美娟， 程玉民. 改进的移动最小二乘法[J]. 力学季刊， 2003， 24（2）： 266-272.

CHEN M J， CHENG Y M. improved moving least-square approximation[J]. Chinese Quarterly of Mechanics， 2003， 24（2）： 266-272.

[7] WANG J F， SUN F X， CHENG Y M， et al. Error estimates for the interpolating moving least-squares method[J]. Applied Mathematics and Computation， 2014， 245： 321-342.

[8] 程玉民， 彭妙娟， 李九红. 复变量移动最小二乘法及其应用[J]. 力学学报， 2005， 37（6）： 719-723.

CHENG Y M， PENG M J， LI J H. Complex variable moving least-square approximation and its application[J]. Chinese Journal of Theoretical And Applied Mechanics， 2005， 37（6）： 719-723.

[9] 程玉民， 李九红. 弹性力学的复变量无网格方法[J]. 物理学报， 2005， 54（10）： 4463-4471.

CHENG Y M， LI J H. A meshless method with complex variables for elasticity[J]. Acta Physica Sinica， 2005， 54（10）： 4463-4471.

[10] ZHANG Z， LI D M， CHENG Y M， et al. The improved element-free Galerkin method for three-dimensional wave equation[J]. Acta Mechanica Sinica， 2012， 28（3）： 808-818.

[11] ZHANG Z， WANG J F， CHENG Y M， et al. The improved element-free Galerkin method for three-dimensional transient heat conduction problems[J]. Science China Physics， Mechanics & Astronomy， 2013， 56（8）： 1568-1580.

[12] ZHANG Z， HAO S Y， LIEW K M， et al. The improved element-free Galerkin method for two-dimensional elastodynamics problems[J]. Engineering Analysis with Boundary Elements， 2013， 37（12）： 1576-1584.

[13] WANG J F， SUN F X， CHENG Y M. An improved interpolating element-free Galerkin method with nonsingular weight function for two-dimensional potential problems[J]. Chinese Physics B， 2012， 21（9）： 090204.

[14] SUN F X， WANG J F， CHENG Y M. An improved interpolating element-free Galerkin method for elasticity[J]. Chinese Physics B， 2013， 22（12）： 120203.

[15] CHENG Y M， BAI F N， PENG M J. A novel Interpolating Element-Free Galerkin （IEFG） method for two-dimensional elastoplasticity[J]. Applied Mathematical Modelling， 2014， 38（21/22）： 5187-5197.

[16] PENG M J， LI R X， CHENG Y M. Analyzing three-dimensional viscoelasticity problems via the Improved Element-Free Galerkin （IEFG） method[J]. Engineering Analysis with Boundary Elements， 2014（40）： 104-113. DOI： 10.1016/j.enganabound.2013.11.018.

[17] CHENG Y M， PENG M J. Boundary element-free method for elastodynamics[J]. Science in China： Series G， Physics， Mechanics & Astronomy， 2005， 48（6）： 641-657.

[18] PENG M J， CHENG Y M. A Boundary Element-Free Method （BEFM） for two-dimensional potential problems[J]. Engineering Analysis with Boundary Elements， 2009， 33（1）： 77-82. DOI： 10.1016/j.enganabound.2008.03.005.

[19] CHENG Y M， LIEW K M， KITIPORNCHAI S. Reply to ‘Comments on ‘Boundary element-free method （BEFM） and its application to two-dimensional elasticity problems[J]. International Journal for Numerical Methods in Engineering， 2009， 78（10）： 1258-1260.

[20] REN H P， CHENG Y M， ZHANG W. An Improved Boundary Element-Free Method （IBEFM） for two-dimensional potential problems[J]. Chinese Physics B， 2009， 18（10）： 4065-4073.

[21] CHENG Y M， LI J H. A complex variable meshless method for fracture problems[J]. Science in China： Series G， Physics， Mechanics & Astronomy， 2006， 49（1）： 46-59.

[22] 刘沛， 彭妙娟， 程玉民. 势问题的复变量无单元Galerkin方法[J]. 计算机辅助工程， 2009， 18（4）： 11-15.

LIU P， PENG M J， CHENG Y M. Complex variables element-free Galerkin method for potential problems[J]. Computer Aided Engineering， 2009， 18（4）： 11-15.

[23] PENG M J， LIU P， CHENG Y M. Complex Variable Element-Free Galerkin（CVEFG） method for two-dimensional elasticity problems[J]. International Journal of Applied Mechanics， 2009， 1（2）： 367-385.

[24] PENG M J， LI D M， CHENG Y M. Complex Variable Element-Free Galerkin（CVEFG） method for elasto-plasticity problems[J]. Engineering Structures， 2011， 33（1）： 127-135.

[25] 李冬明， 彭妙娟， 程玉民. 弹性大变形问题的复变量无单元Galerkin方法[J]. 中国科学： 物理学 力学 天文学， 2011， 41（8）： 1003-1014.

LI D M， PENG M J， CHENG Y M. Complex Variable Element-Free Galerkin（CVEFG） method for elastic large deformation problems[J]. Scientia Sinica （Physica， Mechanica & Astronomica）， 2011， 41（8）： 1003-1014.

[26] CHENG Y M， LI R X， PENG M J. Complex variable element-free Galerkin method for viscoelasticity problems[J]. Chinese Physics B， 2012， 21（9）： 090205.

[27] CHENG Y M， WANG J F， LI R X. Complex Variable Element-Free Galerkin（CVEFG） method for two-dimensional elastodynamics problems[J]. International Journal of Applied Mechanics， 2012， 4（4）： 1250042.

[28] BAI F N， LI D M， WANG J F， et al. An Improved Complex Variable Element-Free Galerkin（ICVEFG） method for two-dimensional elasticity problems[J]. Chinese Physics B， 2012， 21（2）： 020204.

[29] CHENG Y M， WANG J F， BAI F N. A new complex variable element-free Galerkin method for two-dimensional potential problems[J]. Chinese Physics B， 2012， 21（9）： 090203.

[30] WANG J F， CHENG Y M. A new complex variable meshless method for transient heat conduction problems[J]. Chinese Physics B， 2012， 21（12）： 120206.

[31] WANG J F， CHENG Y M. New complex variable meshless method for advection-diffusion problems[J]. Chinese Physics B， 2013， 22（3）： 030208.

[32] DENG Y J， LIU C， PENG M J， et al. The interpolating complex variable element-free Galerkin method for temperature field problems[J]. International Journal of Applied Mechanics， 2015， 7（2）： 1550017.

[33] 马翔， 倪富健， 陈荣生. 复合式机场道面载荷应力[J]. 长安大学学报， 2010， 30（4）： 23-27.

MA X， NI F J， CHEN R S. Load stress of composite airport pavement[J]. Journal of Changan University（Natural Science Edition）， 2010， 30（4）： 23-27.

[34] 马翔， 倪富健， 顾兴宇. 复合式机场道面结构设计方法[J]. 交通运输工程学报， 2010， 10（2）： 36-40.

MA X， NI F J， GU X Y. Structure design method of composition airfield pavement[J]. Journal of Traffic and Transportation Engineering， 2010， 10（2）： 36-40.

[35] 林小平. 复杂条件下机场跑道沥青加铺层结构设计理论与方法[D]. 上海： 同济大学， 2007.

（编辑 武晓英）