炸高对侵彻效应影响试验和数值模拟研究*

崔智丽，徐浩铭，经来旺

(1.安徽理工大学 理学院，淮南 232001；2.中国人民解放军96172部队，景德镇 333000)



炸高对侵彻效应影响试验和数值模拟研究*

崔智丽1，徐浩铭2，经来旺1

(1.安徽理工大学 理学院，淮南 232001；2.中国人民解放军96172部队，景德镇 333000)

摘要:为了研究炸高因素对爆炸成型弹丸(EFP)成型性能及侵彻深度的影响，利用有限元软件LSDYNA，建立了球缺罩型聚能装药仿真计算模型。研究了十种不同炸高条件下，EFP着靶时性能参数和侵彻45#钢靶过程，并与该装药静破甲试验结果进行了对比分析。结果表明：试验与数值模拟结果较吻合，最大误差为10%，EFP装药的有利炸高与装药直径之比为3.9～4.4，最大破甲深度约为装药直径的0.92倍。

关键词:爆炸成型弹丸; 数值模拟; 炸高; 侵彻

聚能装药开孔技术相对于费时费力的传统机械钻孔法，具有简单快速且效费比高等特点。通过聚能装药爆炸产生的爆炸成型弹丸(EFP)，对装甲钢、岩石等目标进行开孔侵彻，并形成一定直径和深度的开孔，该项技术在军事领域中已经得到广泛应用。EFP是由药型罩金属经炸药爆炸锻成的，开始形成时破片处于流动状态，经过一段时间后这种流动状态结束，EFP头尾速度趋于一致，形成一枚坚实完整的弹丸，EFP侵彻靶板的机理即不同于动能弹，又不同于金属射流，而是介于两者之间。研究和试验表明[1-3]，EFP的侵彻性能与其速度和比动能密切关系，所以优化EFP着靶时状态参数是提高EFP侵彻能力有效途径。

1数值模型

1.1装药结构选择

选择刘建青、顾文彬等等优化设计得到的φ 65 mm球缺型变壁厚EFP[3]，装药结构长径比N=1.0；药型罩采用紫铜材料，罩顶厚δ=2.1 mm、罩内表面曲率半径r1=67 mm、外表面曲率半径r2=62 mm，如图1所示。

1.2材料方程的选取

聚能装药爆炸、药型罩压垮、EFP形成及拉伸、EFP侵彻钢靶、串联EFP装药成型及其侵彻钢靶等过程是一种多物质相互作用的大变形运动。目前，对EFP的数值模拟研究大多采用Langrage算法，由于在Langrage算法中考虑空气需要定义空气与弹丸的接触面，弹丸成形过程中会因空气网格大的变形而出现负体积，导致计算无法进行下去，所以Langrage算法计算模型中常忽略空气对弹丸成型的影响，这与实际不相符合，用该方法难以准确模拟[4-7]。

材料受到外荷载时的动态响应主要表现为变形、流动和断裂。其动态响应的描述是一个非常复杂的过程，一般采用状态方程和本构方程来描述。材料的状态方程是一个关系到压力、密度和一些热力学参数(内能和温度)的关系式，它反映了材料的体积特性；而本构方程则体现了材料的偏向应变，它与材料的应变、应变率、内能以及晶粒大小有关。模型中各部分所用材料的本构模型与状态方程如表1、表2、表3、表4所示。

表1　仿真计算中采用的材料模型和状态方程

表2　JH-2炸药计算参数

表3　紫铜计算参数

表4　45#钢计算参数

1.3模型的建立

本次EFP侵彻钢靶过程数值模拟，装药采用中心点起爆方式起爆，炸高为250 mm，钢靶直径为110 mm，厚度为100 mm，图2为EFP侵彻钢靶数值模拟整体网格图。

2炸高影响分析

2.1不同炸高条件下EFP着靶时性能分析

在不同炸高条件下，EFP的侵彻效应与其接触靶板时刻的状态有直接关系。

图3为不同炸高下EFP到达靶板时，即开始侵彻靶板前EFP形态的计算结果对比图。表5为到达靶板时EFP各项参数，l为EFP长度，vj为EFP头部速度，vm为EFP中部速度，vt为EFP尾部速度。

对于一定结构的EFP装药，不同时刻爆炸形成的EFP其状态是确定的。由于炸高不同，侵彻靶板开始时刻的EFP状态区别很大，不同炸高导致EFP破甲前长径比和速度梯度分布不同。炸高越小，EFP形成不充分，速度梯度还比较大，长度没有达到最大，直径较粗；炸高越大，EFP拉伸越充分，直径越小，速度梯度较小，侵彻威力越强。本质而言，EFP长径比和速度梯度分布特性决定其破甲效果。

2.2EFP侵彻钢靶过程数值模拟

图4为EFP侵彻钢靶过程的数值模拟，图5为侵彻深度随时间T变化的P-T曲线。

通过分析以上结果和侵彻深度时程曲线，得知EFP侵彻钢靶过程如下：

100 μs时刻EFP开始接触靶板，至110 μs时刻形成一个比EFP直径稍大的弹坑，此阶段属于EFP侵彻的开坑阶段。

从110 μs时刻EFP稳定侵彻靶板开始到孔底部扩大区形成的135 μs时刻，EFP侵彻靶板有比较稳定的形态，开孔直径变化不大，侵彻速度稳定，此阶段EFP侵彻时间约为25 μs，占整个侵彻过程时长的45%，侵彻深度为3.5 cm，约占整个侵深的60%左右，此阶段属于EFP侵彻的稳定阶段。

从135 μs时刻开始，EFP速度已降至1100 m/s左右，且速度下降很快，靶板的强度作用越来越明显，侵彻能力变得很弱，155 μs时刻之后，失去侵彻能力的EFP残留体在孔底部产生激荡，此阶段属于侵彻的终止阶段。

2.3不同炸高条件下EFP侵彻钢靶数值模拟

分别对2.1节中的10种炸高条件下EFP侵彻钢靶过程进行仿真计算，图6分别为仿真计算的最终侵彻效果。

表6为EFP对靶板侵彻成孔参数，表中H为炸高，D为药型罩直径，d1为入孔直径，P为侵彻深度。

图7为侵彻深度P随炸高H变化曲线数值模拟结果，图8为开孔直径d1随炸高H变化曲线数值模拟结果。对比表6结果可以发现，炸高小于240 mm时，随着炸高的增加，EFP着靶前不断拉伸，速度和长径都不断增长，使得侵彻钢靶时的深度也不断增加，但随着EFP的拉伸，开孔孔径却在逐渐减小；炸高大于240 mm时，侵彻前EFP的性能变化趋于稳定，侵彻效果也基本不变。

由以上结果可以看出，炸高在120～240 mm区间时，随着炸高的增加，EFP着靶前被拉伸，速度分布和长径比变化都较快，长度增加而直径变小，长径比增大，比动能逐渐增加，这样就使得侵彻钢靶的深度也在增加，孔径却在逐渐减小，堆积作用变得越来越不明显；炸高在大于240 mm之后，侵彻前EFP的速度分布和长径比变化较小，特别是在炸高大于300 mm之后，其变化已经很小，EFP的拉伸基本完成，长径比变化不大，侵彻效果也基本保持不变。

2.4实验对比分析

为了验证炸高对EFP装药侵彻性能的影响规律，同时为数值模拟结果提供事实依据，进行了10组不同炸高EFP侵彻验证性实验。实验每组2发取平均值，结果如图9所示，分别为炸高120 mm、240 mm、350 mm三种条件下EFP侵彻钢靶实验结果。

表7为试验值与仿真计算EFP对靶板侵彻成孔参数对比，表中H为炸高，R为装药直径，P为侵彻深度，d1为入孔孔径。图10为试验与仿真计算的P-H对比曲线，图11为试验与仿真计算的d1-H对比曲线。

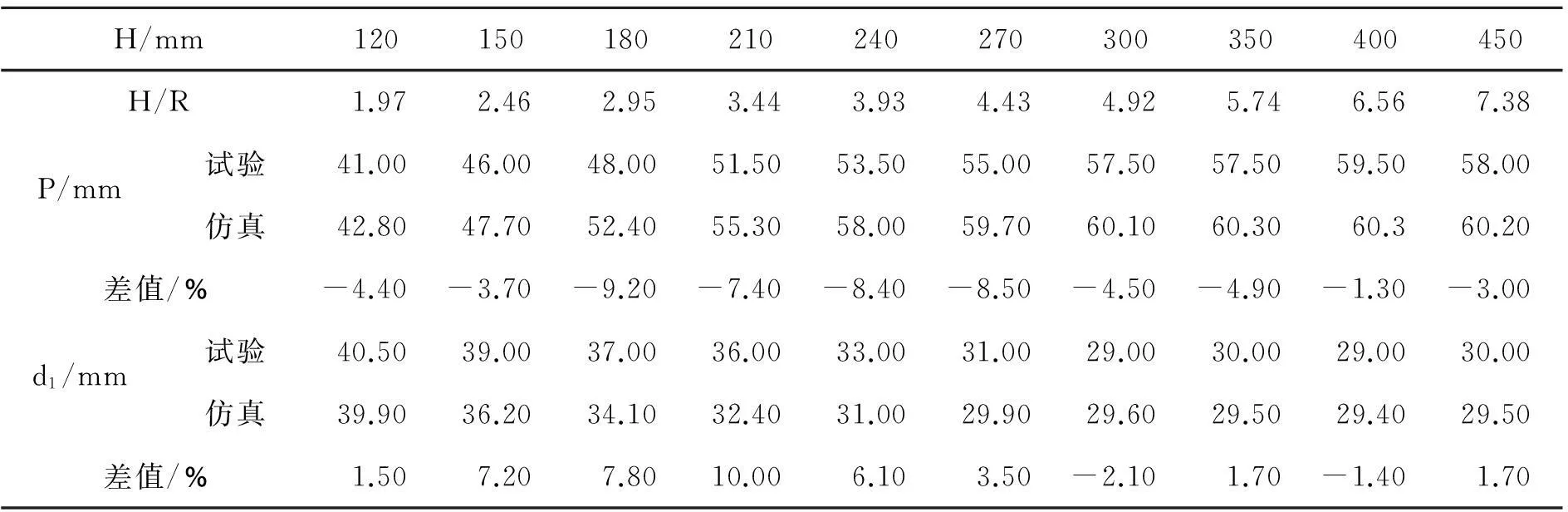
表7　仿真计算与试验结果对比

从对比结果可以看出，侵彻深度的试验值与数值模拟值之间的相对误差最大为-9.2%、最小为-1.3%，入孔孔径的试验值与数值模拟值之间的相对误差最大为10%、最小为-1.4%，均在±10%之内。说明侵彻深度和入孔孔径数值模拟结果与试验情况都吻合较好。

3结论

对不同炸高条件下EFP装药的成型性能和侵彻钢靶过程进行了数值模拟，并进行了验证实验对比分析，研究结论如下：

(1)用ALE流-固耦合算法对EFP的形成和侵彻钢靶过程进行了数值模拟，对EFP战斗部终点效应研究具有实用价值。

(2)通过对比分析表明，数值模拟计算结果与实验结果较吻合，说明建立的模型和选用的参数合理可靠，运用数值模拟与实验相结合的方法，可以较好地研究EFP侵彻效应规律，能大大降低研究的成本。

(3)该EFP装药的有利炸高区间为240 mm至270 mm，最大侵彻深度约为装药直径的0.92倍。

参考文献(References)

[1]ANDREOPOULOS J,RODI W.Experimental investigation of jets in a cross flow[J].Journal of Fluid Mechanics,1984,138:93-127.

[2]王成,恽寿榕,黄风雷.同口径破-破型串联装药战斗部的试验研究[J].弹箭与制导学报,2002,22(2):61-65.

[2]WANG Cheng,YUN Shou Rong,HUANG Feng Lei.Experiment study on the forward charge blast effect on the follow-through charge of tandem warhead[J].Journal of Projectile,Rockets Missiles and Guidance,2002,22(2):31-34.(in Chinese)

[3]徐浩铭，顾文彬，唐勇，等.串联EFP装药结构参数优化实验研究[J].爆炸与冲击2013,33(3):287-291.

[3]XU Hao-ming，GU Wen-bin，TANG Yong，et al.Experimental study on structural parameter optimization of tandem explosively-formed projectile charges[J].Explosion and Shock Waves，2013,33(3):287-291.(in Chinese)

[4]顾文彬,刘建青,唐勇，等.球缺型EFP战斗部结构优化设计研究[J].南京理工大学学报(自然科学版),2008,32(2):165-168.

[4]GU W B,LIU J Q,TANG Y,et al.Optimizing design of EFP warhead with hemispherical liner[J].Journal of Nanjing University of Science and Technology (Nature Science)，2008,32(2):165-168.(in Chinese)

[5]孙承纬，卫玉章，周之奎.应用爆轰物理[M].北京：国防工业出版社，2000.

[6]桂毓林,于川.带尾冀的翻转型爆炸成型弹丸的三维数值模拟[J].爆炸与冲击,2005,25(4):313-318.

[6]GUI Y L,YU C.3D simulation of over-turned explosively formed projectile(EFP)with star-shaped fins[J].Explosion and Shock Waves，2005,25(4):313-318.(in Chinese)

[7]白金泽.LS-DYNA3D理论基础与实例分析[M].北京：科学出版社，2005.

Experimental and Numerical Investigation of Blasting Height Effect on Penetration Properties

CUIZhi-li1,XUHao-ming2,JINGLai-wang1

(1.Anhui University of Science and Technology,Huainan 232001，China；2.PLA 96172 Corps,Jingdezhen 333000,China)

Abstract:In order to study the relationship between blasting height and the penetration depth,the finite element software LSDYNA was used to simulate the penetration process of the EFP shaped charge,and the EFP performance and penetration ability under different blasting height were also discussed by comparing with experiment results.The results show that the experimental date was similar to the numerical simulation.The EFP showed better performance when the ratio of effective blasting height versus diameter of shell-bottom was about 3.9～4.4,and the ratio of maximum penetration depth versus the charging diameter was 0.92.

Key words:EFP; numerical simulation; blasting height; penetration

doi:10.3963/j.issn.1001-487X.2016.02.008

收稿日期:2016-04-07

作者简介:崔智丽(1979-)，女，硕士、讲师，主要从事岩石动态断裂研究，(E-mail) zhlcui@aust.edu.cn。

基金项目:国家自然科学基金重点项目(煤炭联合基金项目)(No.51134025)

中图分类号:O358

文献标识码:A

文章编号:1001-487X(2016)02-0039-06