基于PCA和KPCA的带式输送机故障诊断

张登山（神东煤炭集团公司大柳塔煤矿，陕西　神木　719315）



基于PCA和KPCA的带式输送机故障诊断

张登山（神东煤炭集团公司大柳塔煤矿，陕西神木719315）

摘要：由于在生产过程中监测变量的高度相关性，一个故障或扰动的发生会导致许多变量采样值的异常，因此仅仅检测各个过程变量不足以应用于过程监测、故障诊断。本文通过获得正常操作状态下的数据，采用主元分析对生产过程进行监测，并确定过程运行的统计控制限。当统计量的值超过它们的控制限时，就预示着有故障发生。

关键词：主元分析；故障诊断；过程监控

1　算法说明

1.1PCA和过程监测与故障诊断

PCA是Principal component analysis的缩写，中文翻译为主元分析。它是一种对数据进行分析的技术，最重要的应用是对原有数据进行简化。正如它的名字：主元分析，这种方法可以有效地找出数据中最“主要”的元素和结构，去除噪音和冗余，将原有的复杂数据降维，揭示隐藏在复杂数据背后的简单结构。它的优点是简单，而且无参数限制，可以方便地应用于各个场合。因此应用极其广泛，从神经科学到计算机图形学都有它的用武之地。被誉为应用线性代数最有价值的结果之一[1]

由于生产过程中监测变量的高度相关性，一个故障或扰动的发生会导致许多变量采样值的异常。因此，仅仅检测各个独立的过程变量对于过程监测、故障诊断并无益处。以主元分析（PCA）为代表的多元统计分析方法将生产过程中大量高度相关的过程变量投影到一个包含有原空间绝大多数信息的低维空间中，从而使得过程监测工作大为简化。多元统计监测通过获得过程正常操作状态下的数据，借助一定的数学手段对过程的动态特性进行描述，即获得过程正常操作状态下的数学模型。通过参考过程状态模型，应用观测到的过程动态数据监测突发事件及不规则性，即可以用过程的正常状态模型作为判断系统工作状态的标准。

为了利用主元模型对生产过程进行监测，需要由过程正常运行的数据来确定过程运行的统计控制限。为此引入确定主元模型的平方预测误差（squared prediction error，SPE）（或称为Q）统计量控制限、T2统计量控制限等。当统计量的值超过它们的控制限时，即预示着有故障发生[2]

1.2控制图原理

控制图是对过程质量特性值进行测定、记录评估，从而监测过程是否处于控制状态的一种用统计方法设计的图[3]图上有中心线CL（central line）、上控制界限UCL（Upper control limit）、下控制界限LCL（Lower control limit），如图1所示。

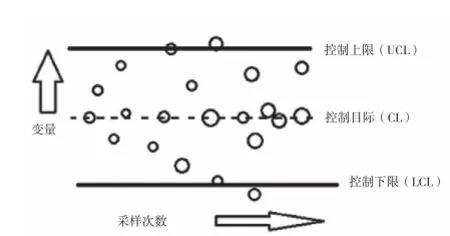
图1　控制图

对于一个生产过程，不管它被如何精心设计和精心维护，总存在着一定量的固有的或自然的变化。它是由许多偶然因素形成的偶然波动的累积效果，由于这种波动比较小，所以我们认为这时生产过程处于受控状态或称为稳态。受控状态是生产过程追求的目标。此外，在生产过程中有时也发生由异常因素造成的异常波动，如由于设备调整不当、人为差错或原材料的缺陷而导致的质量波动。与偶然波动相比，这种异常变化要大的多，而且往往表现出一定的规律和趋势，此时我们认为生产过程处于失控状态，如果不采取措施而继续发生下去，就可能出现危险[4]

令M为度量某个质量特性的统计样本。假定M的均值为µ，标准差为σ。于是，中心线、上控制限和下控制限分别为：

其中k为中心线与控制界限之间用标准差σ为单位所表示的间隔宽度[5]

当不存在系统误差时，产品的质量特性（总体X）服从正态分布，样本点x出现在区间内的概率为：

2　带式运输机故障诊断样本点设定

通过对数据库Drgonsoft中表dbo.T_Result_Realtime中带式运输机工作实时数据的分析，初步设置样本点。

针对一台设备（instrument），一共设置了0～11个监测点；另外统计一个部门监测设备大概在6台左右。现假设一个部门监测的是一个生产活动[7]因此第一种样本点设置如式（3）所示：

此样本是一个生产活动中，所有设备监测点在同一时间的监测数据构成。如果我们从Drgonsoft数据库中取出一个部门一天的监测数据作为研究样本，此样本集构成如下矩阵：

显然上述样本点的设置过程是针对于一个部门活动整体为研究对象设置的，如果想了解部门生产活动中子活动的规律，相应的设置样本点集如下：

式（5）中每一行是同一监测点，不同时间的实时数据，样本集共采集了同一监测点一天内的监测数据。

为了了解一个部门不同子活动之间的关系，可以设置如下样本点集：

其中每行代表不同监测点，同一时间的监测数据。下面的过程，我们将用PCA算法针对以上每个样本集进行分析[8]

3　PCA的实现过程

3.1程序实现

安装PCA工具包：

安装步骤：

（1）在输入窗口输入：install.packages()弹出选择镜像网站窗口，如图5所示。

图3　PCA故障诊断过程

图4　R的版本信息

选择china的任一网站，点击“确定”。

（2）在弹出窗口中，选择要安装的程序包，本次安装psych程序包。

点击确定即开始安装。在安装过程中会安装一些依赖程序包，安装需要访问外网，请保证网络可用。提示安装成功，则安装完成。如果程序包下载不完全会安装失败，请选择网速较快的环境进行安装[9]

图5

图6

图7

实际中为了保证一天数据的有效性，我们对样本整体取到470个样本点（有效地规避了数据的缺失值），首先用summary函数，观察每个观测点的几个基本统计量：最小值、最大值、四分位数和数值型变量的均值[10]

通过协方差函数（cor）来观察每一个自变量之间的相关性，然后用ellipse包中的plotcorr函数作图如图8所示。

其中易发现协方差矩阵为对角阵，圆形的面积越小相关性越大，对角线上的元素为一条直线，因为那是元素与其本身，相关性为1。

图8中发现有很多空白行或列，那是由于在原始的样本数据中，有多个观测点一天内的数据恒为零，这样导致协方差矩阵里面有很多相关数据都是无法计算的，为了避免这种情况，删除了数据中恒为零的观测点，并用R语言程序包corrgram，绘出协方差矩阵对应相关系数的图，图9中蓝色为正相关颜色越深相关性越大，红色为负相关颜色越深负相关性越强。

图8

图9

图10给出了相应元素位置的相关系数的具体数值。

通过上面的分析，对样本数据有了一个初步的认识，下面将通过工具包psych中关于PCA的“碎石图”对样本主元做一个初步判断：

图10

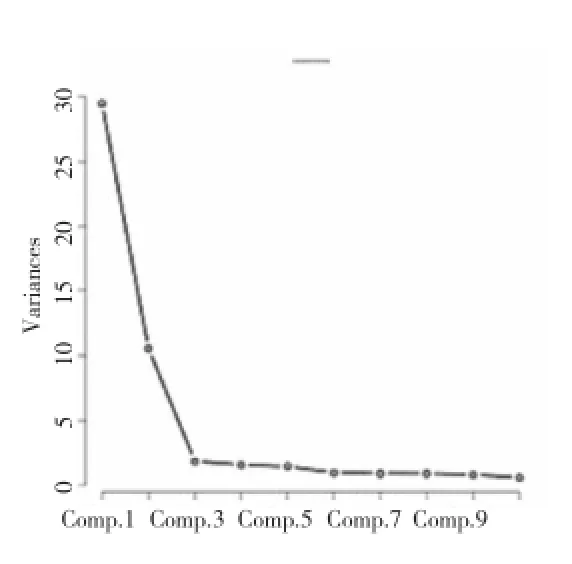
图11　样本碎石图

从图11中易发现前三个主元，所占的信息比重已经很大，尤其第一个主元所包含的信息量是相当大的[11]

4　结语

通过本文所述，通过获得正常操作状态下的数据，采用主元分析对生产过程进行监测，并确定过程运行的统计控制限。当统计量的值超过它们的控制限时，就预示着有故障发生。

参考文献：

[1] 黄民, 魏任之. 矿用钢绳芯带式输送机实时工况监测与故障诊断技术[J]. 煤炭学报, 2005, 30(2): 245 - 250.

[2] 田鹤, 韩刚. 信息融合技术在带式输送机故障诊断中的应用[J]. 矿山机械, 2011, 39(3): 47 - 50.

[3] 王洪平, 吴谦. 带式输送机常见故障与处理[J]. 现代面粉工业, 2010(3): 29 - 32.

[4] 杨玉花. 带式输送机故障诊断及处理方法[J]. 山东煤炭科技, 2009(6): 23 - 24.

[5] 杨庆宏, 张安宁, 陶选等. 带式输送机输送带纵向撕裂保护装置的研究[J]. 煤炭机械, 2006, 27(7): 139 - 140.

[6] 陈义强, 何继兰. 带式输送机常见纵向撕裂的预防措施的探讨[J]. 煤炭工程, 2008(12): 86 - 88.

[7] 张安宁, 孙宇坤, 尹中会等. 带式输送机防纵撕裂保护现状及趋势[J] .煤炭科技技术, 2007, 35(12): 77 - 79.

[8] 王彦凤, 邱常明, 刘英林等. 带式输送机输送带的防偏纠偏研究[J]. 煤质技术, 2007(3): 55 - 57.

[9] 杨政. 带式输送机输送带跑偏的分析及处理[J]. 科技情报开发与经济, 2005, 15(17): 260 - 261.

[10] 李新军. 带式输送机胶带跑偏原因分析与处理[J]. 西北煤炭, 2007, 5(4): 50 - 51.

[11] 刘民. 带式输送机输送带跑偏的分析及处理[J]. 同煤科技, 2004(1): 32 - 34.

文献标识码：B

文章编号：1003-0492（2016）04-0098-04中图分类号：TP273

作者简介

张登山，男，毕业于太原理工大学电气工程系工业自动化专业，现就职于神东煤炭集团公司大柳塔煤矿。

News[新闻]

沈阳38家企业、高校、科研院所等组建机器人产业联盟

2016年4月7日，由沈阳新松机器人自动化股份有限公司牵头，联合东北大学、中国科学院沈阳自动化研究所、沈阳机床（集团）设计研究院有限公司、沈阳高精数控技术有限公司等由 38家企业、高校、科研院所、金融机构等组建的“沈阳市机器人产业联盟”（以下简称“联盟”）在沈阳成立。

沈阳发展机器人产业具有产业规模大、增长速度快、研发水平高、产品种类全、人才保障强等优势。近年来，沈阳市委、市政府相继出台各类支持政策，支持并促进沈阳市机器人及智能装备产业发展，提高机器人及智能装备产业链相关企业竞争力，加强企业、高校、科研院所间的合作交流，构建协同发展的产业集群和更广泛的市场应用。

沈阳市市长潘利国在联盟成立仪式上表示，“政府、企业、学校、科研院所、金融”五位一体的机器人产业联盟正式成立，是沈阳贯彻落实《中共中央国务院关于全面振兴东北地区等老工业基地的若干意见》文件精神、国家系统推进全面创新改革实验和建设国家自主创新示范区的又一举措，必将对沈阳机器人产业快速发展、产业结构调整、实现老工业基地振兴发挥巨大作用。他希望沈阳机器人产业能够做大做强，形成机器人研发、技术研究、零部件配套供应、机器人工程应用等完整的产业群体，促进沈阳机器人整体技术水平的提高。

沈阳市政府秘书长连茂君就沈阳市机器人产业发展的相关政策进行说明。沈阳新松机器人自动化股份有限公司总裁曲道奎、中科院沈阳自动化研究所机器人学国家重点实验室刘连庆副主任、中科院中国工程院院士王天然就打造沈阳成为世界级机器人产业基地、机器人研发的创新成果和机器人发展趋势做主题报告。

Fault Diagnosis Based on PCA and KPCA Belt Conveyor

Abstract:Due to the high correlation of monitored parameters in the production process, a fault or disturbances occur may lead to abnormal of many variables. Therefore, it is insufficient for process monitoring and fault diagnose only by detecting each process variable. According to the data of normal operation state, we use the principal component analysis to monitor the production process, and determine the control limits of the process operation. The fault may occur when the test statistic values exceed the control limit.

Key words:PCA; Fault diagnosis; Process monitoring