基于Riccati方程的动态传感器分配算法*

左　燕，郭宝峰，谷　雨，徐松柏

（杭州电子科技大学信息与控制研究所，杭州　310018）



基于Riccati方程的动态传感器分配算法*

左燕，郭宝峰，谷雨，徐松柏

（杭州电子科技大学信息与控制研究所，杭州310018）

摘要：针对组网跟踪系统传感器分配算法计算量过大的问题，提出了一种基于Riccati方程的动态传感器分配算法。该算法通过Riccati方程离线计算各传感器组合跟踪下的稳态滤波协方差，根据稳态滤波协方差与期望协方差的接近程度动态分配传感器资源。仿真结果显示，与传统协方差控制和贪婪算法相比，基于Riccati方程的动态传感器分配算法在大大减少计算量的同时能够保持较好的跟踪性能。该方法能够更好地应用于大规模传感器组网目标协同跟踪系统。

关键词：多传感器管理，传感器分配，协方差控制，Riccati方程，目标跟踪

0　引言

随着现代战争环境的日益复杂，通过配置多个传感器组网进行协同探测，可以提高防空预警体系对目标的探测和跟踪效果［1］。如何合理分配有限的传感器资源，充分发挥传感器的认知能力，最大限度地获取所需目标信息已成为军事领域研究的重点。在多传感器目标跟踪系统中引入传感器管理是在跟踪性能和传感器资源之间建立一种平衡，以达到系统整体性能最优。

传感器分配算法是传感器管理算法中的一个重要组成部分，该算法的核心是依据一定的准则，建立一个易于量化的目标效能函数，通过优化效能函数获得最优传感器组合进行目标跟踪［2］。国内外学者从不同的角度评估目标跟踪性能，在此基础上提出了不同的效能函数：滤波估计协方差［3 - 5］、信息增益［6 - 7］、Kullback-Leibler分辨力［8］、Reyi信息差异［9］、CRLB［10］，PCRLB［11］等。通过在线遍历所有可能的传感器组合，实现最大化目标效能函数下的资源优化分配，然而随着系统中传感器数目的增加，上述传感器分配算法的计算量急剧增长。为了降低计算量，部分研究者将启发式贪婪算法引入传感器分配算法中［12-14］。通过每次选取“最佳”传感器构造传感器组合进行目标跟踪，减少传感器分配算法的计算量，然而该算法是以选择非最优传感器组合为代价来减轻计算代价。另一方面，部分研究工作集中在设计稳态传感器分配算法［15-16］，即根据各传感器对目标的稳态滤波协方差来进行资源分配，当目标进入稳态跟踪时，能够保证传感器资源的优化分配。然而稳态传感器分配方法是一种开环的分配方法，无法适用于动态变化的环境。如何减少算法的在线计算量，同时保证目标跟踪性能是将传感器管理应用于大规模网络化目标协同跟踪的关键。

本文以雷达组网防空预警系统为背景，结合Riccati方程和协方差控制思想提出了一种基于Riccati方程的动态传感器分配算法。该方法采用Riccati方程离线计算出所有传感器组合对应的稳态滤波协方差，通过期望协方差与稳态滤波协方差的匹配来选择一个最优的组合进行滤波跟踪。最后将本方法与传统协方差控制和贪婪算法进行了仿真比较研究。

1　传感器分配模型

假设N个三坐标（3D）雷达构成的雷达网对空中运动目标进行组网跟踪。传感器组合的集合为D（不包括空集的组合），Dj为第j种传感器组合，所有可能的传感器组合个数为2N-1。动态传感器分配算法的一般优化模型可描述为：

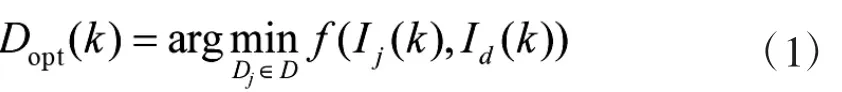
式中：D为传感器组合的扩展集合，Dopt为最优传感器组合；Ij为第j种传感器组合下的性能指标；Id为期望的性能指标；f（·）为效能函数。

在实际应用中，多传感器组网协同跟踪问题通常都会有一些预期的指标，比如目标的期望跟踪精度。基于协方差控制的传感器分配方法［3-5］为目标设定期望的跟踪精度，即期望协方差，根据滤波估计协方差和期望协方差的接近程度进行传感器资源分配。基于协方差控制的传感器分配模型可描述如下

其中，Pj（k|k）表示第j种传感器组合下的滤波估计协方差阵，Pd（k）表示期望协方差阵；f（·）为两个矩阵的度量，用于描述实际协方差和期望协方差阵之间的差异，本文采用矩阵求迹。

传感器分配问题是一个组合优化问题，对于传感器组合的选择一般都是采用全遍历搜索方式。基于协方差控制的传感器分配算法在线遍历搜索时，算法的计算复杂度为O（2Nn3），N为传感器个数，n为目标状态向量的维数。随着组网中传感器个数的增加，传感器在线分配算法的计算量呈几何倍的增加，计算量过大则很可能会造成失跟。

2　基于Riccati方程的动态传感器分配方法

基于协方差控制的传感器分配算法需要每一时刻根据各传感器组合的滤波估计协方差与期望协方差的接近程度来动态分配传感器组合进行目标跟踪［3 - 5］。大量仿真分析发现，经过一段时间之后，目标跟踪进入稳态阶段，各传感器组合的滤波估计协方差达到一个稳态值。基于滤波估计协方差与期望协方差的协方差控制分配结果维持不变。直到期望协方差发生变化，传感器分配需要动态调整。因此，综合考虑跟踪性能和计算效率，本文提出了一种基于Riccati方程的动态传感器分配方法。该方法采用Riccati方程离线计算出所有传感器组合对应的稳态滤波协方差，通过期望协方差与稳态滤波协方差的匹配来选择一个最优的组合进行滤波跟踪。

2.1基于Kalman滤波的Riccati方程

假设目标在三维空间作匀速直线运动，其运动方程为：

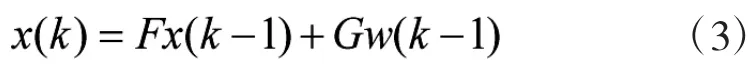
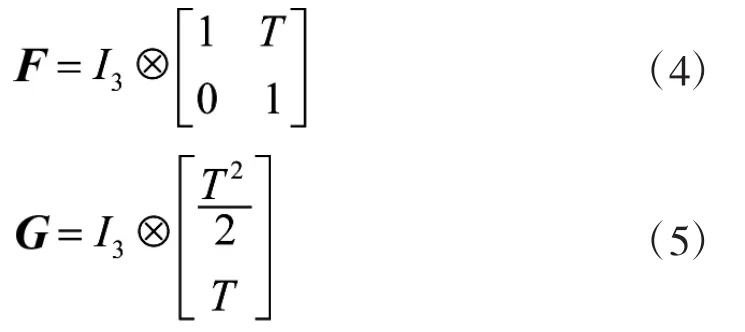
式中，T表示采样间隔，⊗为矩阵直积的运算符号。传感器的量测方程为

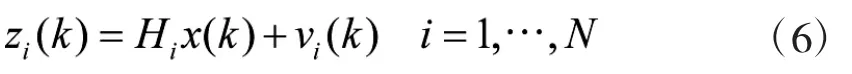
其中，zi（k）是第i个传感器在k时刻的量测值，；vi（k）表示量测噪声，假定为零均值高斯白噪声，服从vi（k）：N（0，Ri）分布，Ri为第i个传感器的量测噪声协方差矩阵。Hi为观测矩阵

Kalman滤波器预测协方差为：

对任一传感器组合Dj（假设包含S个传感器）构成的多传感器跟踪系统，其观测矩阵H和量测噪声R分别为

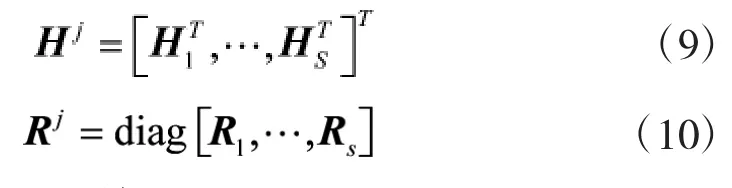
由更新方程可得：

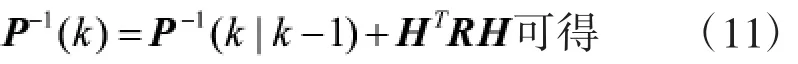
Pj（k）=（（Pj（k|k-1））-1+（Hj）TRjHj）-1

将式（11）代入式（8）可得：

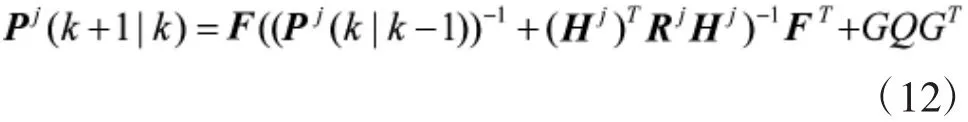
根据矩阵求逆引理：（A+BD-1C)-1=A-1-A-1B

，得到预测协方差矩阵的代数Riccati方程为：

其稳态解形式如下：

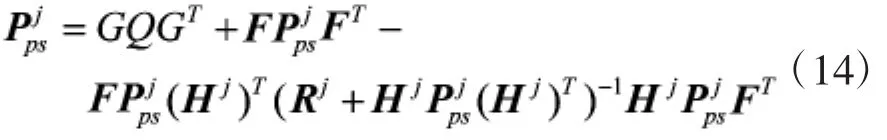
其中，Pjps表示传感器组合Dj组网跟踪下稳态预测协方差矩阵。

由文献［15］可知，对Kalman滤波器，滤波估计协方差最终要趋于稳态值。将式（14）代入式（11）中，得到传感器组合Dj组网跟踪下稳态的滤波估计协方差矩阵Pjfs为：

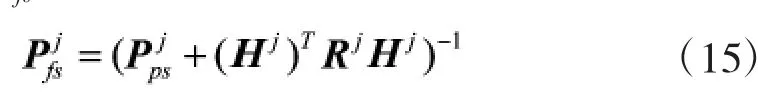
由式（9）和式（10）可知，对于不同的传感器组合，Hj和Rj不同。根据式（14）和式（15）可以离线计算所有传感器组合情况下的稳态滤波协方差。

2.2基于Riccati方程动态传感器分配算法

基于Riccati方程的动态传感器分配方法根据各传感器组合的稳态滤波协方差与期望协方差的接近程度来分配传感器组合进行目标跟踪，它保证在稳态情况下的跟踪性能满足期望跟踪精度（见图1）。

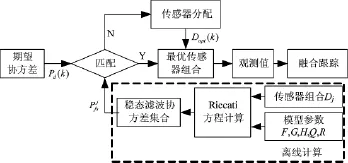
图1　基于Riccati方程的动态传感器分配方法

由式（14）和式（15）可知，当目标运动模型和量测模型参数（F，G，H，Q，R）已知且固定不变的情况下，可以利用Riccati方程离线计算出不同组合下的稳态滤波协方差。

在k时刻，通过选择与期望协方差最匹配的稳态滤波协方差对应的传感器组合作为最优传感器组合进行分配

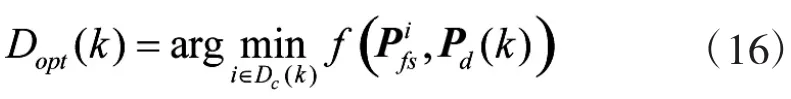
其中，Pjps表示第j种传感器组合下的稳态滤波协方差矩阵，可由式（13）离线计算；Pd（k）表示期望协方差矩阵；f（·）为两个矩阵的度量，用于描述实际协方差和期望协方差阵之间的差异，本文f（·）采用绝对值求迹的方法。

在k+1时刻，若目标期望协方差不发生变化，则不再作搜索比较，继续采用上一时刻获得的最优传感器组合Dopt（k）进行目标探测和滤波跟踪；当目标的期望协方差发生变化时，重新分配传感器组合。

基于Riccati方程的动态传感器分配算法具体步骤如下：

Step 1：初始化：k=1，设置目标状态转移矩阵F，噪声分布矩阵G，各传感器观测矩阵H，以及过程噪声协方差Q和量测噪声协方差R。

Step 3：在线分配。

Step（3a）初始化j=1；

Step（3b）选择k时刻第j种传感器组合Dj；

Step（3d）令j=j+1，返回Step（3b），直到

Step 4：令k=k+1，若期望协方差Pd（k）不发生改变，则直接采用上一时刻的最优传感器组合Dopt（k-1）来进行目标探测和滤波跟踪。否则，返回Step3，重新分配新的传感器组合。

与传统基于协方差控制的动态传感器分配算法相比，本文提出的基于Riccati方程的动态传感器分配算法利用Riccati方程离线计算稳态滤波协方差矩阵集合，在线只需要比较稳态滤波协方差与期望协方差的匹配程度，计算量可大大减小。同时通过稳态传感器分配控制协方差水平在一定范围。一旦确定最优传感器组合，在整个过程中若目标期望协方差不发生变化，则维持当前的最优传感器组合，避免传统的协方差控制算法出现频繁切换传感器组合的情况，减小了传感器管理的负担，提高了传感器管理的效率，增加了算法的实用性。

3　仿真结果与分析

仿真场景是一个由10部雷达构成的传感器阵列对一个目标进行观测，每部雷达都测量目标的x、y、z坐标，雷达的采样间隔为1 s，量测噪声参数如表1所示。

表1　雷达的量测噪声参数　单位：m

目标采用CV模型，两个坐标轴上的加速度为相互独立的零均值高斯白噪声，且具有相同的标准差1m/s2，目标的状态向量记为。目标的初始位置在（1 000， 1 500，2 500）m，x方向的速度为200 m/s，y方向的速度为150 m/s，z方向的速度为300 m/s，采用周期为1 s。期望协方差设为对角阵，为了检验算法对协方差的控制能力，期望协方差分为不同的两段设置，第一段设置成diag［28，3.1，37.3，3.5，39，3.7］，从99 s开始，设置成diag［52.6，4.24，67.9，4.75，70.35，4.7］。

将本文提出的离线Riccati方程的在线传感器分配算法与传统协方差控制［5］和贪婪算法［14］进行仿真比较，度量指标均采用绝对值求迹，仿真结果如图2和图3所示。

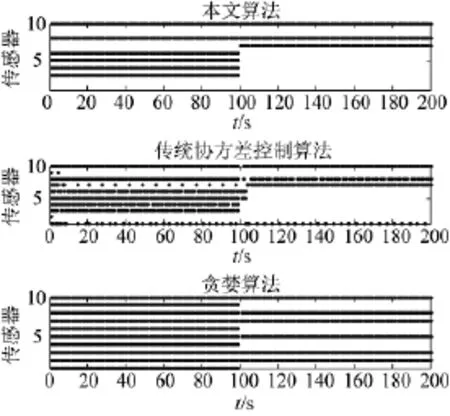
图2　3种算法的传感器资源分配情况

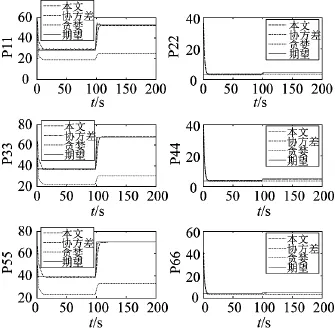
图3　各种算法的滤波估计协方差与期望协方差的对角元素比较

经过50次Monte Carlo仿真，发现基于Riccati方程的动态传感器分配算法和贪婪算法运算的matlab仿真平均耗时分别为0.001 2 s和0.001 1 s，而传统的协方差控制算法的平均耗时为0.500 2 s，可以发现算法在减少计算量上取得了明显的效果（不同的仿真平台耗时也会不同）。

图2给出了各种算法的传感器分配情况，图3给出了各种算法滤波估计协方差与期望协方差之间的对角元素的对比。

①在仿真时间99 s之前，因为期望的跟踪精度较高，3种算法的分配结果都使用了较多的传感器资源。其中基于Riccati方程的动态传感器分配算法使用了最少的传感器资源且在不切换传感器组合的情况下很好地满足了协方差控制要求；传统的协方差控制算法虽然也能很好地满足协方差控制要求，但是出现了频繁切换传感器资源的现象；贪婪算法也能满足一定的协方差控制要求，但是过度地使用了传感器资源。

②从仿真时间99 s之后，随着期望跟踪精度的下降，传感器资源的使用都明显减少，基于Riccati方程的动态传感器分配算法和传统的协方差控制算法分配结果相近，两种算法较好地满足了协方差控制要求。但是贪婪算法使用了更多的传感器资源，未能较好地达到协方差的控制要求。

通过上述分析可得，在计算效率方面，基于Riccati方程的动态传感器分配算法和贪婪算法都能大大提高计算效率，计算效率优于传统协方差控制算法。在协方差控制效果方面，基于Riccati方程的动态传感器分配算法比贪婪算法增加很少的额外计算量，可以找到一个更接近最优组合的传感器组合，从而使传感器分配能够选择较少的传感器资源来满足目标所需的协方差水平。基于Riccati方程的动态传感器分配算法在减少计算量提高计算效率和协方差控制水平上都取得了很好的效果，进而使传感器分配可以应用于大规模雷达组网目标跟踪系统中。

4　结论

为了解决多雷达组网目标跟踪系统中传感器动态分配方法计算量太大无法应用于实际系统的问题，本文给出了一种基于Riccati方程的动态传感器分配算法。该方法通过离线计算Riccati方程获得各传感器组合下的稳态滤波协方差。在线判断期望协方差和稳态滤波协方差的接近程度动态分配传感器资源进行目标跟踪。仿真结果表明，该方法能够在大大减少计算量的同时保持较好的跟踪精度控制，具有一定的工程应用价值。本文研究了单目标情况下的传感器分配方法，在此基础上研究多传感器多目标跟踪下的传感器分配是下一步研究工作的重点。

参考文献：

［1］叶朝谋，丁建江，李庭胜，等.雷达探测资源管理技术分析与评估［J］.现代雷达，2012，34（3）：6-11.

［2］何友，王国宏，关欣.信息融合理论及应用［M］.北京：电子工业出版社，2010.

［3］NASH J M. Optimal allocation of tracking resources［C］// Proceedings of IEEE Conference on Decision and Control，New Orleans，LA，1977：1177-1180.

［4］KALANDROS M. Covariance control for multisensor systems ［J］. IEEE Transactions on Aerospace and Electronic Systems，2002，38（4）：1138-1157.

［5］周文辉.相控阵雷达及组网跟踪系统资源管理技术研究［D］.长沙：国防科学技术大学，2004.

［6］MCINTYRE G A，Hintz K J. Sensor measurement scheduling：an enhanced dynamic preemptive algorithm［J］. Optical Engineering，1998，37（2）：517-523.

［7］刘先省，周林，杜晓玉.基于目标权重和信息增量的传感器管理方法［J］.电子学报，2005，33（9）：1683-1687.

［8］SCHMAEDEKE W W，KASTELLA K D. Information-based sensor management and IMMKF［C］// Proceeding of SPIE on Signal and Data Processing of Small Targets. Orlando，FL，USA，1998：390-401.

［9］KREUCHER C M，KASTELLA K D，HERO Iii A O. Information-based sensor management for multitarget tracking［C］// Proceeding of SPIE on Signal and Data of Small Targets. San Diego，CA，USA. 2003：480-489.

［10］童俊，单甘霖.基于Cramer-Rao下限的多传感器跟踪资源协同分配［J］.宇航学报，2012，33（9）：1314-1321.

［11］杨小军，马祥，宋青松，等.基于条件后验克拉美-罗下界的目标跟踪传感器管理［J］.控制理论与应用，2013，30（5）：543-548.

［12］KALANDROS M，PAO L Y，HO Y C. Randomization and super-heuristics in choosing sensor sets in target tracking applications［C］// Proceedings of IEEE Conference Decision and Control，1999：1803-1808.

［13］方海涛，田康生，周红阳.超启发式传感器选择算法［J］.火力与指挥控制，2006，31（5）：29-32.

［14］徐松柏，左燕，谷雨，等.雷达组网多传感器选择快速启发式算法［J］.杭州电子科技大学学报，2014，34（2）：32-35.

［15］周文辉，胡卫东，郁文贤.基于Riccati方程的稳态传感器分配算法研究［J］.系统工程与电子技术，2004，26 （7）：863-866.

［16］童俊，单甘霖.基于修正Riccati方程与Kuhn-Munkres算法的多传感器跟踪资源分配［J］.控制与决策，2012，27（5）：747-751.

Study on Dynamic Sensor Allocation Algorithm Based on Riccati Equation

ZUO Yan，GUO Bao-feng，GU Yu，XU Song-bai
（Institute of Information and Control，Hangzhou Dianzi University，Hangzhou 310018，China）

Abstract：A dynamic multi-sensor allocation algorithm based on the Riccati equation is proposed to deal with the computational burden of the sensor allocation problem in the multi-sensor tracking system. The algorithm calculates the stable covariance with the Riccati equation outline and dynamically allocates the optimal sensor sets based on the difference between the expected covariance and the stable covariance. Simulation results show that the algorithm can obtain the better tracking accuracy and computation efficiency comparing with the traditional covariance control algorithm and the greedy algorithm. The algorithm can be applied to the multi-sensor collaborative tracking in large-scale sensor networks.

Key words：multi-sensor management，sensor allocation，covariance control，Riccati equation，target tracking

中图分类号：TN953

文献标识码：A

文章编号：1002-0640（2016）05-0046-05

收稿日期：2015-04-16修回日期：2015-05-18

*基金项目：国家自然科学基金（61004119，61375011）；国家“973”计划基金资助项目（2012CB821204）

作者简介：左燕（1980-），女，江西井冈山人，副教授。研究方向：信息融合与多传感器管理技术等。