考虑维修效率的油料装备维修任务分配问题研究

文/ 陆思锡 周庆忠 熊 彪



考虑维修效率的油料装备维修任务分配问题研究

文/ 陆思锡 周庆忠 熊 彪

摘 要：油料装备维修效率对油料装备战时保障能力具有重要影响。本文针对在油料装备维修力量有限的条件下如何通过合理的任务分配，使完成油料装备维修任务的总效率最高的问题，建立了考虑维修效率的油料装备战时维修任务分配模型，并针对可能出现的情况对模型进行了讨论，利用匈牙利算法对模型进行了求解。通过模型的运用表明，考虑维修效率的油料装备战时维修模型可以更好地对维修任务的分配进行优化，确保油料装备总维修效率最高。

关键词：油料装备；维修；效率；决策

信息化条件下，为了使油料装备维修能够有效进行，必须对油料装备维修任务进行高效、合理地分配，尤其是油料装备易暴露，损坏率高，维修任务大，经常会面临因维修力量不足，而使战损油料装备无法及时恢复保障能力的情况。因此，在油料装备维修力量十分有限的战场环境条件下，如何对油料装备维修力量进行合理地分配，使完成各项油料装备维修任务的总效率最高，是需要迫切解决的问题。

1.油料装备战时维修任务分配模型建立

1.1油料装备战时维修任务分配问题的数学描述

假设在油料装备维修任务中，有m个油料装备维修小组，要完成n项维修任务，且不同的维修小组的维修保障能力不完全相同，第i个小组完成第j项油料装备维修任务的效率为eij( i ,j∈ [1, n ])，且≥0，则油料装备战时维修决策的最终目标是通过对维修任务的分配，使完成n项油料装备维修任务的总效率最高，即油料装备的维修耗时最少。为了达到维修耗时最少的目标，引入0～1决策变量pij，当分配第i个维修小组完成第j项任务时，pij=1，否则pij=0。

1.2模型建立

由于受到战时各种复杂因素的影响，在油料装备维修过程中可能出现油料装备维修力量不足等情况，因此，模型的建立分别基于不同的情况来考虑。

①m＞n，且每个维修小组仅分配一项维修任务，第j项任务可由aj个小组共同完成，则此时的维修任务分配模型可描述为：

上述模型中待求的未知数为aj。

②m＜n，每项任务仅由一个维修小组来完成，但是第i个小组可完成bi项任务，此时的决策模型可描述为：

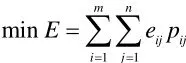
上述模型中待求的未知数为bi。

③每个维修小组最多可分配一项维修任务，且每项任务只由一个维修小组完成，则此时的任务分配模型可描述为：

2.油料装备战时维修任务分配模型求解

从上述建立的维修任务分配模型可以看出，油料装备战时维修任务分配问题实质是一种规划问题，求解规划问题的方法较多，有表上作业法、单纯形法、匈牙利算法等，但表上作业法和单纯形法对于考虑维修效率的任务分配模型求解比较复杂，因此，本文采用更为有效的匈牙利算法对模型进行求解。

2.1匈牙利算法基本原理

匈牙利算法的基本原理是构造效益矩阵，从效益矩阵出发来确定任务分配的最优方案。利用匈牙利算法解决油料装备维修任务分配问题时，要求m=n，即维修任务与维修小组的数量相同。对于上述三种情况的模型，当m=n时，可直接利用匈牙利算法进行求解，在效率矩阵中寻找分布在不同行、不同列的n个独立的0元素，并且使这些元素的和最小，对于其它两种情况的模型则需构造广义效益矩阵来求解[1]。广义效益矩阵就是在效益矩阵的基础上构造虚拟的维修任务，或虚拟的油料装备维修小组来使维修任务和维修小组的数量相等，来达到利用匈牙利算法求解的要求，但不影响真实的油料装备维修任务分配。

2.2模型求解方法

①当m＞n时，可以先安排一个维修小组来完成一项维修任务，则剩下m-n个维修小组，可将其剩下的每个小组分配给n项维修任务中的任何一个，则每项任务都有另外的m-n个虚拟任务，且每个维修小组完成虚拟任务的效益值完全一样，则维修任务数就变为n（m-n+1）个，多于维修小组数量。假设还有n （m-n+1）-m个小组，完成任何维修任务的效益都最小，则可构造广义效益矩阵：

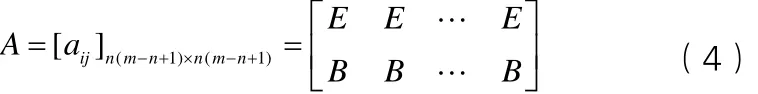
式中，第一行有m-n+1个E={ eij}m× n；B的值是E中每列效益最小的数，为（m-n）（n-1）行n列矩阵。则当m＞n时，决策模型的解就可根据广义效益矩阵A所对应的最优解[pij]n( m- n + 1)×n ( m- n + 1)前m行中等于1的元素来确定。

②当m＜n时，先给每个维修小组安排一项维修任务，则剩下n-m项维修任务，每项任务可由m个维修小组完成，假设每个小组都存在另外n-m个与其完全相同的虚拟小组，这些虚拟小组完成每项任务的时间完全一样。则维修小组数量就达到n （n-m+1），可确保每项维修任务有且仅有一个维修小组来完成[2]。假设还有m（n-m+1）-n项虚拟任务，其由任何一个维修小组完成的效益值都最小，则可构造广义效益矩阵：

式中，第一行有n-m+1个ET，BT为m行（n-m）（m-1）列矩阵。则当m＜n时，决策模型的解就可根据广义效益矩阵A所对应的最优解[pij]m( n- m + 1)× m ( n- m + 1)前n列中等于1的元素来确定。

③当每个维修小组最多可分配一项维修任务，且每项任务只由一个维修小组完成时，可分三种情况考虑。若m=n，则可利用匈牙利算法直接求解[3]；若m＞n，即任务少，则添加虚拟维修任务，在效率矩阵添加m-n列0元素，构成m×m的效率矩阵；若m＜n，即维修小组少，则添加虚拟维修小组，在效率矩阵添加m-n行0元素，构成n×n的效率矩阵。

3.油料装备战时维修任务分配模型应用

某次油料保障中，需要对油料装备进行快速抢修以恢复其油料保障能力。现有5项不同的油料装备维修任务，其中任务R1非常紧急，对维修时间要求较高，R2、R5两项任务较为重要，对维修时间有一定要求，剩余两项任务对时间要求不高，目前可同时对上述任务进行维修的油料装备维修小组有4个，为了保证油料装备的维修效率，每个维修小组最多可分配一项维修任务，且每项任务只由一个维修小组完成。各维修小组完成不同任务所需时间的效率值如下表所示，下面对上述油料装备维修任务的分配进行分析。

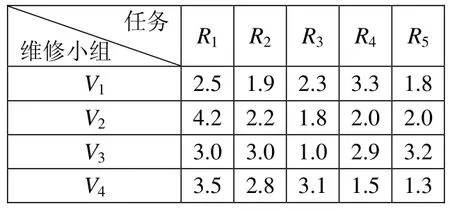
各油料装备维修小组维修效率值

对上述问题的具体情况进行分析可知，该问题属于所建立的决策模型中的第3类问题，由于R1非常紧急，优先对任务R1进行分配，根据上表中的数据得到效率矩阵E：

则E1=[2.5 4.2 3.0 3.5]T，因此，对于维修任务R1来说，维修小组V1完成该任务的效率最高，首先将油料装备维修任务R1分配给V1。

由于每项任务只由一个维修小组完成，因此，在考虑剩余任务时，不考虑V1，剩余3个维修小组完成R2、R5两项任务的效率矩阵为：

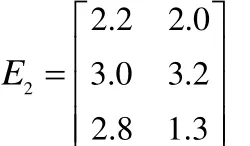
根据 中效率值可知，R2、R5任务的分配方案是： R2→V2，R5→V4。

最后对剩下的任务进行分配。由于只剩下维修小组V3，其对R3、R4的效率矩阵为E3=[1.0 2.9]，因此应将R3分配给V3。对于最后剩下任务R4，由于各维修小组已全部分配任务，则需等待维修小组完成其它任务后再完成该任务。于是对与任务R4，可计算各维修小组对已分配任务的效率与承担任务R4效率之和，并派最小值对应的维修小组去完成任务R4。经计算，V4的效率最高，为2.8，因此，将任务R4分配给V4。

于是得到最终的油料装备维修任务分配方案： 完成任务R1， 完成任务R2， 完成任务R3， 先完成任务R5，再完成任务R4。

4.结语

维修任务的分配，直接影响到油料装备战时维修保障工作效率，特别是在战时条件下，维修任务重、时间紧，油料装备维修任务分配工作，对油料装备维修效率的影响更大。本文在考虑维修效率的基础上，建立了维修任务分配模型，可以在战时复杂条件下得到油料装备维修任务的优化分配方案，使得在维修力量有限的情况下，能够更高效地完成油料装备战时维修任务。

（作者单位：解放军后勤工程学院）

参考文献

[1]张惠珍，马良． 一种基于匈牙利算法的二次分配问题求解方法[J]． 数学的实践与认识． 2009， 39（13）：121～130．

[2]栾飞，杨玮． 基于匈牙利算法的自动化立体仓库出入库优化调度[J]． 陕西科技大学学报． 2011， 29（3）：122～125．

[3]于焕英，孙晚华，何峣． 基于匈牙利算法的多车型配送问题[J]． 物流技术． 2011， 6：74～75．