最大熵与MP-CLEAN方法对扩展源图像重建的比较
2016-07-11张茂林周建锋
张茂林,周建锋
(1. 清华大学工程物理系天体物理中心,北京 100084;2. 粒子技术与辐射成像教育部重点实验室(清华大学),北京 100084)
最大熵与MP-CLEAN方法对扩展源图像重建的比较
张茂林1,2,周建锋1,2
(1. 清华大学工程物理系天体物理中心,北京100084;2. 粒子技术与辐射成像教育部重点实验室(清华大学),北京100084)
摘要:在射电综合成像领域,通常需要用退卷积的方法补全频域稀疏的采样。由于扩展源的频域信息更为丰富,要补全这些信息相对于点源来说更难,因此扩展源的图像重建是射电综合成像领域的一大难点。为了探索射电干涉扩展源图像重建方法的特点,将最大熵与一种加速的CLEAN方法(文中称之为Multi-Point CLEAN,MP-CLEAN)对扩展源的干涉阵模拟数据的图像重建进行了比较。通过比较,发现对于同样的观测数据,两种方法都能较好地重建图像,但MP-CLEAN方法的旁瓣祛除效果与重建效果优于最大熵方法,而且在模拟数据重建中MP-CLEAN方法的总体速度比最大熵快3倍以上。最后,在讨论部分通过研究两种方法中参数的选择对重建结果的影响,发现最大熵方法比MP-CLEAN方法对参数选择的依赖性弱,这表明最大熵方法有更好的鲁棒性。
关键词:图像重建;射电干涉阵;Multi-Point CLEAN;最大熵方法;扩展源
射电天文是天文学的一个分支,射电天文顾名思义是通过探测射电波观测天体,从而研究天体的一门科学。射电波的波长相对于可见光长得多,这使得射电观测的角分辨率受到很大的限制,以6 cm的射电波为例,其波长是可见光(波长400至760 nm)的十万倍左右,也就是说,一个1 m直径的光学望远镜的分辨率相当于直径约100 km的射电望远镜,显然分辨率是射电天文发展的一个很大的阻碍。从19世纪40年代起,干涉成像技术的发展克服了这种局限。干涉成像技术的创始人Martin Ryle也因此获得了1974年的诺贝尔奖。接下来的数十年,一些大型的射电干涉阵列(如One-Mile Telescope、 Green Bank Interferometer、 Westerbork Synthesis Radio Telescope、 Very Large Array)陆续建成,大大推动了射电天文学的发展。如今的射电干涉望远镜已经跨入世界上分辨能力最高的望远镜行列,例如阿塔卡玛毫米/亚毫米波阵列望远镜(Atacama Large Millimeter Array, ALMA)的空间分辨能力已经是哈勃空间望远镜(Hubble Space Telescope)的5倍左右。
干涉阵是利用干涉原理得到可见度数据(Visibility Data),这里的可见度数据可等效理解为图像的空间频谱数据。由于干涉是来自两个信号的相干,所以得到的可见度数据与观测天线的数量及相对位置分布有关。受材料、建造技术及资金等限制,现实中只能建造天线数目和尺寸都有限的干涉阵。但是,随着干涉技术的不断发展和完善,人们已经开始筹建越来越大的阵列,例如我国的 “天籁计划” 等,由此也带来了数据处理的挑战[1]。干涉阵的排布对成像有较显著的影响,这方面国内已有所研究[2]。由于射电干涉阵的观测数据是对图像频域空间的稀疏采样,因此如果直接对获取的可见度数据进行傅里叶逆变换,得到的图像往往很模糊,通常存在很强的旁瓣。为了重建清晰的图像,通常需要进行反卷积(Deconvolution)。在射电天文图像重建领域,常用的几种反卷积方法有CLEAN方法[3-4]及其衍生方法(如Multi-scale CLEAN[5]、Multi-resolution CLEAN[6]等)和最大熵方法[7]及其衍生方法(如Multi-scale MEM[8]等)。射电干涉成像中,扩展源的图像重建是其中的难点,普通的CLEAN方法虽然对简单的点源重建效果较好,但对于复杂的大面积弥散源来说重建时计算量大,收敛速度慢,重建稳定性差,得到的结果通常不理想[9]。具有代表性的适用于扩展源干涉阵数据的重建方法主要有两种:一种是在CLEAN的基础上发展起来的多尺度方法,以Cornwell的Multi-Scale CLEAN[5]为代表,一种是以最大熵方法[7](MEM)为代表。本文使用一种简单的加速CLEAN的方法,与CLEAN方法每次选择残余图中的最亮点不同,每次选择大于最亮点γ(0<γ<1)倍的多个点,而不仅仅是一个[10],这种方法本文称为Multi-Point CLEAN方法(简称MP-CLEAN方法)。这种方法既加速了CLEAN,又在一定程度上利用了相邻像素值之间的物理联系,适合进行复杂扩展源的重建。本文之所以选择用最大熵方法与MP-CLEAN方法进行对比,是由于MP-CLEAN方法的简单性,它并不属于多尺度方法,同样地,最大熵方法也不属于多尺度的方法,二者同属于扩展源重建的初级方法。因此可以将这两种比较初级的方法进行比较,通过对比两种扩展源重建方法,可以了解两种方法的特点,并为进一步完善和改进射电干涉扩展源图像重建方法提供启发。
1模型的建立
为了简化模型,本文中认为天图的可见度数据与天图的空间频谱等效,即直接使用傅里叶频谱数据作为可见度数据。任意给定一个亮度分布I(x,y),其可见度可以用(1)式表示:
(1)
式中,V(u,v)为可见度数据;I(x,y)为亮度分布图像,即可见度是图像的傅里叶变换。射电望远镜的观测等效于在天图的频域进行采样。如果准确获得可见度的全部采样,可以直接利用傅里叶逆变换求得I(x,y),如(2)式:
(2)
然而实际数据往往是对可见度数据的部分采样,采样函数如(3)式:
(3)
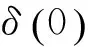
(4)

在重建时,已知数据是采样得到的可见度数据和采样函数(在图像域表达就是已知脏图和点扩展函数),而需要重建真实图像I(x,y)。
如果考虑观测中存在的噪声,可见度观测数据可以用下式表示:
(5)
式中,V(uk)表示可见度观测数据;I(xi)表示真实亮度分布;uk是UV平面(频域)上第k个采样点的位置向量;xi是图像平面第i个像素的位置向量;nk表示UV平面上第k个采样点的噪声。有了(5)式描述的关系,要求出真实亮度分布,需要用反卷积方法。
2重建方法
2.1最大熵方法
在引入最大熵方法之前先给出一种熵的定义,文[11]于1991年提出了一种熵的形式,如(6)式:
(6)
式中,Hg表示图像的(相对)熵;b表示待重建图像;m表示图像模型;i表示第i个像素。
利用这种熵的定义,结合观测数据,就能求解真实亮度分布。在观测数据的约束下求满足熵最大的解,可以利用拉格朗日乘子法构造目标函数:
(7)
式中,χ2为观测可见度数据与重建图像的可见度数据各点偏差大小的归一化平方和;E(χ2)为χ2的期望值,χ2具体表达式为
(8)
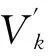
使目标函数取得最大值的图像b就是待求的解,函数的极值问题有多种求解方法,这里不妨转化为求目标函数梯度的0点,即可利用牛顿法求解,迭代步长的具体表达式由下式得到[10]:
(9)
式中,n从0开始取值,b(0)即为已知给定的先验图像m,本文所做模拟中的先验图像m是一张所有点取值为1的图像;J为目标函数;α取常数;q取点扩展函数的主峰峰值。
实现步骤[12]:
(1)给出初始重建图像b0,图像模型m,这里令b0及m所有像素的值等于1;
(2)对重建图像的傅里叶域用采样函数进行采样,得到重采样数据Vk′;
(3)利用重采样数据、观测采样数据及采样函数的有关参数,代入(9)式,求出迭代步长Δb;
(4)更新重建图像:b=b+Δb;
(5)判断迭代终止条件是否达到,即归一化卡方值开始小于等于1。如果达到终止条件,则输出图像b即为重建图像;如果未达到,则返回第(2)步;
(6)将重建图像卷积与最大基线长对应分辨率的高斯函数即得到最终的最大熵重建结果。
2.2MP-CLEAN方法
在射电天文图像重建中,CLEAN方法是最常用的反卷积方法之一,文[10]于1980年提出了一种可以同时对多个点进行CLEAN来加速CLEAN的方法,为了描述和比较方便,本文称之为Multi-Point CLEAN(MP-CLEAN)。在应用MP-CLEAN时,需要一条经验性假设,即有采样较好的数据对应点扩散函数的主瓣比旁瓣高很多,即使有旁瓣的叠加,不同亮源同时作用在同一位置的概率不大,形成假源的峰值也不会太大。这就为同时选择多个真实的源提供了可能,因此可以在每一步迭代中选择大于最亮值γ(0<γ≤1)倍的多个点,而不仅仅是一个点[8]来加速CLEAN。每一次迭代γ允许的取值范围可能不一样,但是,文中为了简便,γ在同一次重建中都取一个较为保守的常数(注γ≡1时为CLEAN方法),参数的选取在文中第4部分详细讨论。下面是MP-CLEAN方法的实现步骤[10]:
(1)给出一个初始模型M0,并令M0所有元素为0;
(2)利用采样函数求出由模型得到的可见度数据;
(3)将模型可见度数据与观测数据作差,再做傅里叶逆变换,取实部得到残差图R;
(4)找出残差图R中的最大值MAX;
(5)找出残差图中大于MAXγ(0<γ≤1)倍的点,作为MP图(与模型尺寸一样的图,图中的点除了找出的这些点与原图位置及像素值一样,其余像素点全为0);
(6)更新模型:在原模型上加MP图的β(0<β<1)倍;
(7)判断是否达到迭代终止条件: 残差图对应的可见度数据的均方根小于等于估计噪声水平(即卡方小于等于1时终止迭代)。如果未达到终止条件,则返回第(2)步。
(8)将结果卷积与最大基线长对应分辨率的高斯函数即得到MP-CLEAN重建结果。
3数值模拟及分析
3.1模拟数据的生成
模拟数据的生成从干涉阵的排列及组合开始,采样函数由天线阵列及观测等因素确定,本文模拟所用的采样函数由排列在同一条直线上的天线组成,其位置参考韦斯特博克综合孔径射电望远镜(Westerbork Synthesis Radio Telescope, WSRT)的天线位置设置。观测时利用地球自身的旋转,一条基线对应的点在采样空间扫过一条弧线。为了简便,用一条弧线表示这种观测。观测时间越长,扫过弧线长度越长,考虑到地球自转的周期性,12小时等效180°的扫描。由于实信号对应的可见度数据具有对称性,因此扫描过程等效于绕着中心直径上的点旋转采样,这里扫描的弧线是椭圆弧,椭圆的长轴与短轴之比为1∶sinθ(这里的θ为被观测源所在的赤纬,文中θ取60°为例)。
选一张扩展源作为原图(图1左上图:图像尺寸为1 200 × 1 200,这里每个像素大小设为1 arcsec × 1 arcsec)做傅里叶变换,即得到可见度(图1右上图),再利用采样函数(图1左下图)对可见度采样并加上噪声就可以得到模拟的可见度观测数据(图1右下图)。干涉阵的最大基线长度决定了其分辨率(在波长一定的情况下),所选的观测波长λ约为6 cm,得到的分辨率约为4.4 arcsec × 5.1 arcsec。由于观测数据分辨率的限制,为了统一分辨率,在后面的重建图像与真图(真图与原图不同,真图是原图卷积高斯函数得到的分辨率为4.4 arcsec × 5.1 arcsec)的比较中,统一卷积一个归一化的二维高斯函数。
由于模拟可见度数据是复数,因此选择的噪声也必须取复数形式,其幅度取服从均方差为5(单位:Jansky, Jy)、均值为0的高斯分布的绝对值,其相位取[0, 2π]上的均匀分布。在后面的模拟中假设知道噪声的大小(即预估的噪声水平是准确的)。
由于采样函数没有对可见度的原点(直流分量)进行采样,即总流量需要估计,而这里模拟中流量估计认为准确,即在频域采样时对可见度的原点多采了一点。数值模拟中输入信息是图1右下图对应的采样得到的可见度数据(即模拟观测数据)、估计的噪声、估计的流量及采样函数。
图1左上:模拟选用的扩展源,单位:Jy;左下:12 h观测对应的采样函数,又称为UV覆盖(uv-coverage),两坐标轴单位都是kλ(1kλ≈60 m);右上:原图可见度数据的幅度的对数,右下:模拟观测(采样)得到的可见度数据(已加噪声)的幅度的对数
Fig.1Top-left panel: extended source chosen for this paper (unit: Jy); Bottom-left panel: the UV coverage of a 12h observation; Top-right panel: the logarithm of the visibility amplitude to the original image; Bottom-left panel: the logarithm of the sampled visibility
利用模拟数据,可以通过最大熵或者MP-CLEAN等方法对真图进行重建。然而由于采样数据本身的缺失,对于模拟中用到的复杂扩展源而言,任何方法重建的结果都不可能恢复到与复杂的原始图像完全一致,因为任何反卷积方法都可看成在缺失的频域采样处插值,重建结果只能是基于一定的模型对真图的近似估计。
3.2模拟重建比较
本文所用模拟中α、β、γ3个参数的选取:α=5、β=0.1、γ=0.6(参数的选取可参看第4部分的讨论,选择这些参数的基本原则是使得收敛的卡方尽可能地接近1且保证重建的稳定性)。
固定上面的几个参数,就可以分别用最大熵及MP-CLEAN对模拟的可见度数据进行重建,得到的重建结果如图2。图2展示了最大熵方法及MP-CLEAN方法利用8 h和12 h的模拟观测数据重建的结果。可以发现直接利用采样数据作傅里叶逆变换得到的脏图(Dirty map)与真图(Ture image)差别很大,主要体现在旁瓣很多,而且有条纹状结构。MP-CLEAN方法和最大熵方法的重建结果在不同程度上抑制了旁瓣,正中间的面源及它的延展结构都恢复得较好,尤其是MP-CLEAN方法,重建的结果很清楚,同时淹没在旁瓣中的点源也得到了较好的恢复,但是,最大熵方法依旧有一部分源没能恢复,而且存在微弱可见的旁瓣。从残余图来看(残余图是重建图像频谱重采样与观测得到的可见度数据做差之后傅里叶逆变换得到),最大熵的残余图中还能依稀看见真图中间面源的影子,也可以看到许多黑色点源的残迹,而MP-CLEAN方法得到的残余图中几乎看不到这些踪迹,这说明MP-CLEAN重建更胜一筹。对比真图、脏图以及重建结果,总体来说两种方法的重建效果较好,重建结构比较清楚,比脏图的效果要好很多。
为了更直观地分析它们之间的差别,在RA=601 arcsec处取一剖面(下文中所有的剖面都是指此位置处的剖面)如图3。表1是从剖面的残差图(此处残差图是指真图减去重建图像得到的图,注意与前面的残余图有区别)图3中得到的几个统计量(由于随机噪声的存在,对于不同次的重建,表1至表3中的所有统计量具有一定的变化幅度,但均值变化幅度小于0.5 Jy,标准差变化幅度一般不超过10%,由于这种变化很小,并不影响两种方法结果的对比分析,因此本文只取某一次重建结果进行分析),均值越接近0且标准差越小,表明越接近真图。最大熵与MP-CLEAN方法重建的图像均值与脏图相比小得多,说明两种方法的重建都保证了总流量恢复得很好。
从标准差来看,MP-CLEAN的结果无论是8 h还是12 h观测中,其标准差都要比最大熵小。从剖面图可以看出,即使在源较弱的图像边缘,MP-CLEAN的结果与真实图像吻合得很好,而最大熵结果还存在微弱的旁瓣难以去除,说明MP-CLEAN的旁瓣抑制效果比最大熵要好。
图2MP-CLEAN及最大熵方法对8 h及12 h模拟观测的重建结果。左上:真图;右上:8 h观测对应的脏图;中间和下面各4幅子图,分别对应8 h和12 h观测数据的重建结果。重建结果中的4幅子图分别为:右上,最大熵重建结果;左上,最大熵结果的残余图;左下,MP-CLEAN重建结果;右下:MP-CLEAN重建的残余图
Fig.2The reconstruction results of the 8h and 12h observations from the MP-CLEAN and the MEM. Top-left panel: the True image; Top-right panel: the dirty image made from the 8h observation. The two four-subplots at the middle and bottom of the image correspond to the 8h and 12h observation respectively. For each four subplots, Middle-left panel: the MEM result; Middle-right panel: the residual of the MEM result; Bottom-left panel: the MP-CLEAN result; Bottom-right panel: the residual of the MP-CLEAN result
表1重建结果剖面残差图的均值及标准差
Table 1The mean and standard deviations of profile
differences from the reconstruction
图3MP-CLEAN及最大熵方法对8 h(上图)及12 h(下图)观测的重建结果的剖面残差图
(在剖面RA=601 arcsec处真图减去脏图、最大熵及MP-CLEAN的结果)
Fig.3The profile difference map of reconstruction results of the 8h (Top subplot) and 12h
(bottom subplot) observation (true image minus other images atRA=601 arcsec)
除了重建的效果,再看两种方法的重建速度,图4给出了最大熵和MP-CLEAN对12 h观测数据进行重建的χ2及残差(绝对值)最大值随迭代步数及时间变化的关系。从图4中χ2与迭代步数之间的关系可以发现,MP-CLEAN只需要不到70步,χ2即达到1,而最大熵则需要140多步。从χ2随时间的变化曲线可以发现,MP-CLEAN只需约15 s,而最大熵则需要55 s左右。结合迭代步数及时间,可以算出MP-CLEAN平均每步运算所需时间为0.2 s左右,而最大熵大约要0.4 s。由此可见MP-CLEAN的每一次迭代的速度约为最大熵方法的两倍,而MP-CLEAN需要的重建步数是最大熵方法的一半,最终导致最大熵方法所需的重建时间是MP-CLEAN的3倍多(接近4倍)。
图4χ2及残差绝对值最大值随迭代步数及时间变化的关系曲线
Fig.4Theχ2and the maximum absolute residual versus the iteration or time
为了进一步检验这两种方法的重建特点,选择更多的原图进行模拟观测,然后重建,采样时间为12 h,采样阵列保持不变。为了体现与上面的扩展源不一样,选用的源一个是规则的源(月球),另一个是两个不规则星系的原图。重建得到的结果如图5,从图5的重建结果不难发现,与前面分析的重建特点一致:流量恢复均较好,都能较好地重建,而且MP-CLEAN对旁瓣的祛除更好,其剖面残差的方差更小。限于篇幅原因,关于这些源重建速度的曲线并未给出,这两个源的实验结果是:第1个源(Source 1)的重建中,MP-CLEAN的迭代时间不到15 s,而最大熵则花了近50 s(是MP-CLEAN的3倍多);第2个源(Source 2)的重建中,MP-CLEAN的迭代时间不到30 s,而最大熵的迭代时间却超过了150 s(是MP-CLEAN的5倍多)。模拟结果表明MP-CLEAN比最大熵快3倍以上,与前面的结果保持一致。
4讨论
在3.2节已经给出了最大熵及MP-CLEAN的重建结果,并且进行了详细的对比分析。然而,最大熵与MP-CLEAN方法的重建效果与重建参数的选择有关,下面是利用前面8 h的观测数据在不同参数选择情况下的重建,通过对比和分析重建结果,进一步了解两种重建方法的特点。
首先改变最大熵方法中的参数α,得到图6中不同α情况下χ2的变化曲线,可以看到如果不断地增大α,χ2会迅速地降到1,重建结果的标准差较大,而如果不断减小α到0附近,那么重建结果与真图就有较大的整体偏差。这可以从表2中看出明显的规律:随着α的增大,均值的变化趋向0,然后稳定在0附近;从标准差来看,随着α的增大,标准差逐渐增大。
图5最大熵及MP-CLEAN方法对于不同扩展源的重建结果。中心线左边为第1个源的重建结果及在RA=377 arcsec
处的剖面残差曲线;中心线右边为第2个源的重建结果及在Dec=601 arcsec处的剖面残差曲线
Fig.5The reconstruction results from the MEM and MP-CLEAN method for different sources. The left panel is the reconstruction
results of Source 1 and the plot of the profile difference map atRA=377 arcsec; the right panel is the reconstruction
results of Source 2 and the plot of the profile difference map atDec=601 arcsec
这与α作用在观测数据上有关,随着α增大,观测数据这个约束的权重越大,所以均值会收敛到0,而熵的权重就相对变小,熵本身是一种平滑性约束,熵权重减小,意味着重建结果的振荡剧烈,所以标准差逐渐变大。在α=0.2时,不难发现旁瓣被抑制了,但是无论从图6中χ2的收敛曲线,还是从表2中的均值来看,重建结果与真图有整体上的偏离。从图6中χ2的变化曲线可以看到,α=0.2时χ2收敛的值远大于1,从表2中的标准差来看,α=0.2时的结果振荡最小,恰恰是熵作为一种平滑性约束的体现。重建结果的剖面残差图如图7,在图7中,除了α=0.2时重建结果与真图有整体的偏移(从表2中对应的均值可以看出),难以看出重建结果之间较明显的差别,这也说明最大熵重建结果对参数的选择有较好的鲁棒性。
下面再看MP-CLEAN方法在γ(0<γ<1)取不同值时的重建情况,从图8中的χ2随迭代的变化曲线可以看到,γ越大则MP-CLEAN方法对扩展源的重建速度越慢,图像重建结果中的振荡也变明显;γ越小则重建结果越平滑,但是重建图像中存在假源的可能性越大,γ越小假源的数目和强度的期望值都会变多和变大,γ太小(如图8中γ=0.1)χ2难以降下来,只能收敛到大于1的值。
重建结果的剖面残差图如图9,可以发现γ取不同的值对重建结果有较显著的影响,对比图9与图7不难发现,最大熵方法在α取不同值时,重建结果之间的差别并不太大,而从表2与表3中的标准差对比中可以定量地说明这一点,因此MP-CLEAN方法对影响其重建结果的参数γ的敏感程度较高,而最大熵则相对鲁棒性更好。从表3中可以发现MP-CLEAN在不同参数取值下均值都接近0,但是方差则呈现中间(γ取0.5~0.7)低,两侧高的总体趋势,这说明MP-CLEAN的参数选择受两方面的约束,一个约束是重建结果中的假源应当数目少而且强度弱,另一个约束是结果的稳定性。前一个约束要求γ尽可能地接近1,因为这样重建结果含有假源的可能性才会变小,后一个约束则要求γ尽可能接近0,在这两个约束的相互作用下,最后就呈现了表3中的方差中间低、两侧高的现象。采样越多越全,γ可以选取的范围越大,越有利于MP-CLEAN的重建。如果采样太少,γ选择的区间就会越小,甚至可能找不到合适的γ,此时再使用MP-CLEAN方法进行复杂扩展源的重建可能难以得到好的结果。
图6不同α取值下χ2的自然对数
随迭代变化的关系曲线
Fig.6The natural logarithm ofχ2versus the
iteration whenαvaries
图7不同α取值下最大熵对8 h观测的
重建结果剖面的残差图
Fig.7The profile differences of the MEM reconstruction
results within the 8h whenαvaries
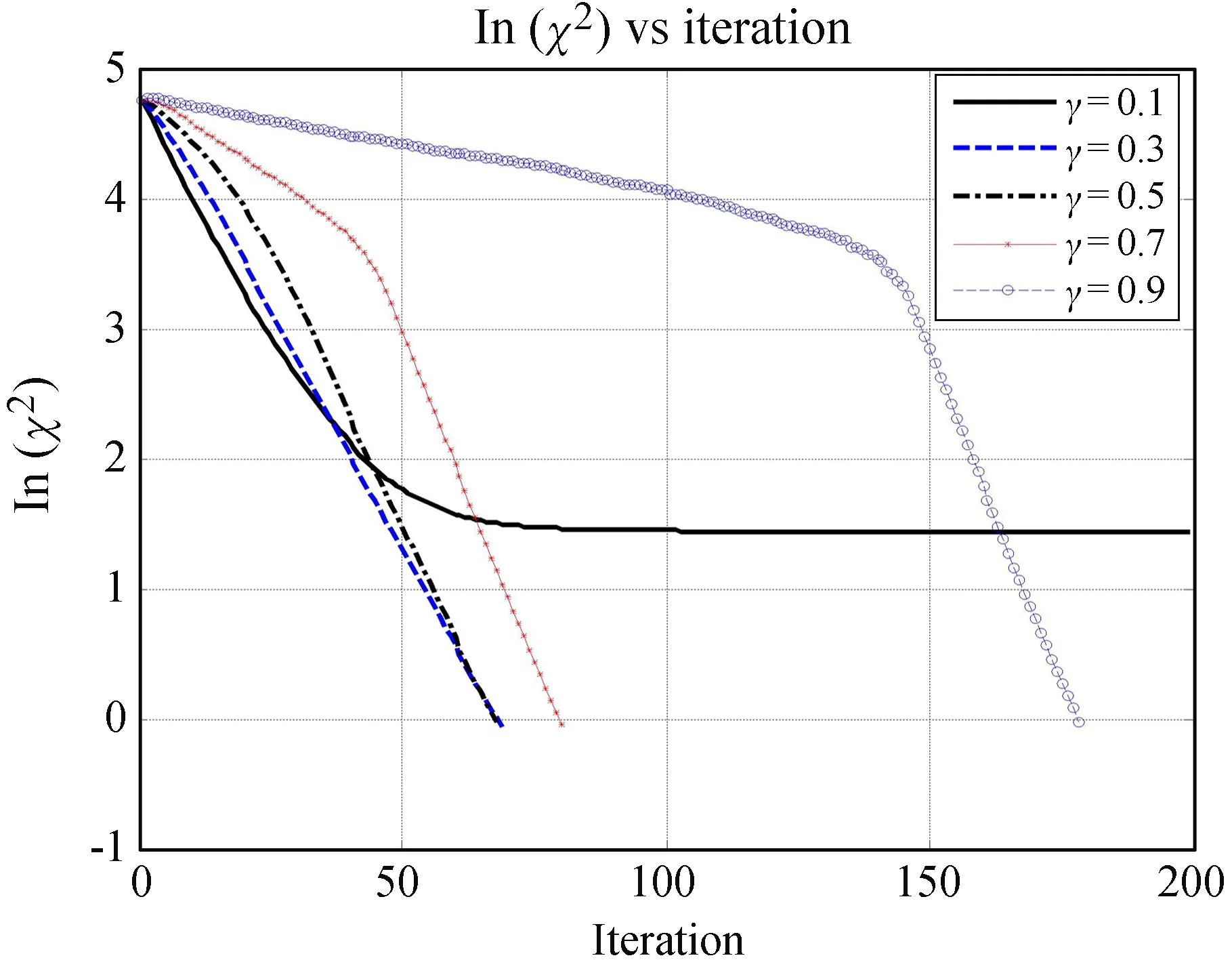
图8不同γ取值下χ2的自然对数
随迭代变化的关系曲线
Fig.8The natural logarithm ofχ2versus the
iteration whenγvaries
图9不同γ取值下MP-CLEAN对8 h观测的
重建结果剖面的残差图
Fig.9The profile differences of the MP-CLEAN recon-
struction results within the 8h whenγvaries
表2最大熵方法在不同α取值下重建图像的
剖面残差的均值及标准差
Table 2The mean and standard deviation of profile
differences using MEM whenαvaries
表3MP-CLEAN在不同γ取值下重建图像
的剖面残差的均值及标准差
Table 3The mean and standard deviation of profile diff-
erences using the MP-CLEAN whenγvaries
由于β的取值对MP-CLEAN的影响主要体现在速度上,对重建图像效果的影响不大(当然β很大时也可能出现一定的不稳定性),因此β对MP-CLEAN重建的影响在此不再赘述。
5总结
本文利用最大熵方法与MP-CLEAN方法对模拟扩展源的可见度数据进行重建,可以发现:
(1)最大熵方法有着比MP-CLEAN更严格的数学迭代形式,MP-CLEAN方法则带有一定的经验性;
(2)对于同样的采样数据,MP-CLEAN对扩展源的重建比最大熵方法重建效果好(使得χ2收敛到1附近时各参数的取值),主要体现在旁瓣降得更低,重建图像与真图之间差别更小;
(3)MP-CLEAN方法的重建速度比最大熵快,从模拟结果来看,总体上所花时间不到最大熵的三分之一;
(4)最大熵方法及MP-CLEAN方法的重建效果与参数的选择有关,最大熵方法对参数的依赖性要小于MP-CLEAN方法,即最大熵方法的鲁棒性优于MP-CLEAN方法。
总而言之,就本文所用的模拟数据及重建结果而言,综合模拟重建图像的效果及重建的速度,MP-CLEAN比最大熵方法有更佳的重建效果及更快的重建速度。然而,由于MP-CLEAN对可见度数据采样的要求较高,而且需要满足源的旁瓣作用在同一位置的概率较小这种经验性的假设,在采样很差(点扩散函数旁瓣峰值接近主峰峰值时)或者在经验性假设不成立时(例如亮源的某些对称性分布导致旁瓣叠加很严重),MP-CLEAN方法从原理上已经不能适用,而最大熵方法理论上依旧能够用于重建,这也是最大熵方法的鲁棒性比MP-CLEAN好的体现之一。但MP-CLEAN方法在一定程度上挖掘了CLEAN方法在同一尺度上的潜能,可以为完善和改进可见度采样较好的扩展源图像重建方法提供更好、更快捷的途径。
参考文献:
[1]田海俊, 徐洋, 陈学雷, 等. 射电干涉阵 GPU 相关器的研究初探[J]. 天文研究与技术——国家天文台台刊, 2014, 11(3): 209-217.
Tian Haijun, Xu Yang, Chen Xuelei, et al. A preliminary study on GPU-based correlators for a radio interferometer array[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2014, 11(3): 209-217.
[2]徐永华, 汪敏, 郝龙飞, 等. 太阳低频射电干涉阵的构建仿真[J]. 天文研究与技术——国家天文台台刊, 2013, 10(3): 242-248.
Xu Yonghua, Wang Min, Hao Longfei, et al. Simulations of a low-frequency solar radio interferometry array[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2013, 10(3): 242-248.
[3]Högbom J A. Aperture synthesis with a non-regular distribution of interferometer baselines[J]. Astronomy and Astrophysics Supplement, 1974, 15: 417-426.
[4]Schwarz U J. Mathematical-statistical description of the iterative beam removing technique (Method CLEAN) [J]. Astronomy and Astrophysics, 1978, 65: 345-356.
[5]Cornwell T J. Multiscale CLEAN deconvolution of radio synthesis images[J]. IEEE Journal of Selected Topics in Signal Processing, 2008, 2(5): 793-801.
[6]Wakker B P, Schwarz U J. The multi-resolution CLEAN and its application to the short-spacing problem in interferometry[J]. Astronomy and Astrophysics, 1988, 200: 312-322.
[7]Gull S F, Skilling J. Maximum entropy method in image processing[J]. IEE Proceedings F, 1984, 131(6): 646-659.
[8]Pantin E, Starck J L. Deconvolution of astronomical images using the multiscale maximum entropy method[J]. Astronomy and Astrophysics Supplement, 1996, 118(3): 575-586.
[9]Cornwell T J. A method of stabilizing the clean algorithm[J]. Astronomy and Astrophysics, 1983, 121(2): 281-285.
[10]Clark B G. An efficient implementation of the algorithm ‘CLEAN’[J]. Astronomy and Astrophysics, 1980, 89(3): 377-378.
[11]Skilling J, Gull S F. Bayesian maximum entropy image reconstruction[J]. Institute of Mathematical Statistics, 1991, 20: 341-367.
[12]Cornwell T J, Evans K F. A simple maximum entropy deconvolution algorithm[J]. Astronomy and Astrophysics, 1985, 143(1): 77-83.
CN 53-1189/PISSN 1672-7673
A Comparison of the MEM and the MP-CLEAN Methods for the Image Reconstruction of Extended Sources with Simulated Visibility Data
Zhang Maolin1,2, Zhou Jianfeng1,2
(1. Department of Engineering Physics and Center for Astrophysics, Tsinghua University, Beijing 100084, China,Email: zhangml13@mails.tsinghua.edu.cn; 2. Key Laboratory of Particle & Radiation Imaging(Tsinghua University) Ministry of Education, Beijing 100084, China)
Key words:Image reconstruction; Radio interferometer array; Multi-Point CLEAN; Maximum Entropy Method; Extended source
Abstract:In the radio synthesis imaging area, the deconvolution is used to fill up the un-sampled points at the Fourier domain. The algorithms like CLEAN and MEM often play an important role in the deconvolution. As extended sources have more complex visibility, the reconstruction for extended sourcesis difficult. In this paper we make a comparison of the MEM (Maximum Entropy Method) with the speed up CLEAN method (named Multi-Point CLEAN in this paper, or MP-CLEAN for short) for extended source reconstruction based on the simulated visibility data. The simulated data are produced by sampling the Flourier Frequency domain for a true image with the sample function generated from a simulated interferometer array. By analyzing and comparing, it is easy to find that both of these two methods work well on the image reconstruction while the MP-CLEAN is better than the MEM for getting rid of the side lobes. The MP-CLEAN is at least 3 times faster than the MEM in our simulations.A deeper analyzing of the selection of parameters shows that the MEM is more independent on the parameters than the MP-CLEAN, which indicates that the MEM is more robust.
基金项目:国家自然科学基金 (11173038, 11373025);清华大学自主科研计划 (20111081102) 资助.
收稿日期:2015-04-16;
修订日期:2015-06-09
作者简介:张茂林,男,硕士. 研究方向:天体物理. Email: zhangml13@mails.tsinghua.edu.cn
中图分类号:P164
文献标识码:A
文章编号:1672-7673(2016)01-0100-11
