基于D-S证据理论的测试性分配方法研究

汤文超,李文海,罗恬颖（.海军航空工程学院，山东　烟台6400；.海军航空工程学院，山东　青岛6604）



基于D-S证据理论的测试性分配方法研究

汤文超1,李文海1,罗恬颖2
（1.海军航空工程学院，山东烟台264001；2.海军航空工程学院，山东青岛266041）

摘要：针对现有测试性分配方法的不足，以及人们判断的模糊性和不确定性这两个问题，将模糊层次分析法引入测试性分配中，先求得层次单排序权重向量，进而求得层次总排序权重向量，根据总排序权重向量求得各组成单元的分配指标。针对传统模糊层次分析法在融合多个专家的评价时只是进行简单的数据相加再求平均这一不足之处，将D-S证据理论运用到融合不同专家的评价中，最后结合案例应用验证该方法的可行性。

关键词：测试性分配；模糊层次分析法；权重向量；D-S证据理论

（9140A27020212JB14311）

0 引　言

测试性分配是将系统的测试性定量要求根据给定的原则和方法，按系统层次自上而下逐级分配给系统的各组成部分[1]。现有的测试性分配方法主要有经验分配法、故障率分配法、加权分配法、有部分老产品时的分配法及优化分配法等[1-2]，这些方法都有各自的特点和具体的适用条件，但是在对产品进行创新设计时，上述方法的分配结果往往不能满足要求。文献[3]将产品复杂程度、测试性实现费用、技术水平、工作时间以及环境条件作为影响测试性分配的5项因素，引入层次分析法（AHP）确定各机构的重要性影响权重系数，求得了分配指标，然而却没有考虑人们的判断具有模糊性和不确定性。文献[4]在融合多个专家的评价时只是进行简单的数据相加再求平均，致使试验结果可能同样不够理想。

本文拟从两个方面对上述问题进行改进：

1）考虑人们判断的模糊性和不确定性，将模糊数引入AHP法。

2）运用D-S证据理论来融合不同专家的评价。

1 证据融合算法

证据理论源于20世纪60年代美国哈佛大学数学家A.P.Dempster在利用上、下限概率来解决多值映射问题方面的研究工作，由其学生G.Shafer发展起来[5]，不同的证据来源具有不同的概率分配函数。Dempster合成规则（Dempster's combinational rule）也称证据合成公式，其定义如下：

对于∀A⊆Θ，Θ上的两个mass函数m1，m2的Dempster合成规则为

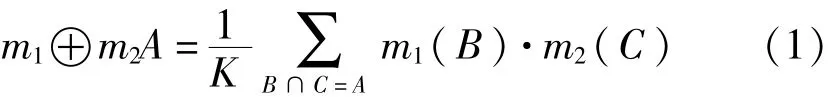
其中K为归一化常数：

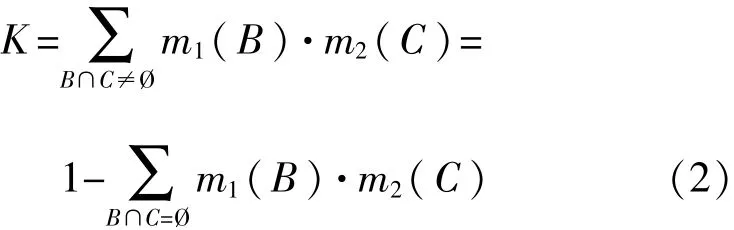
对于∀A⊆Θ，识别框架Θ上的有限个mass函数m1，m2，…，mn的Dempster合成规则为

（m1⊕m2⊕…⊕mn）（A）=

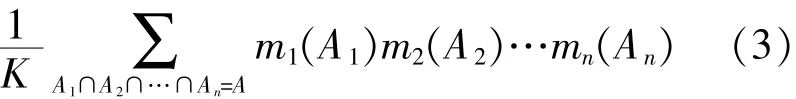
其中

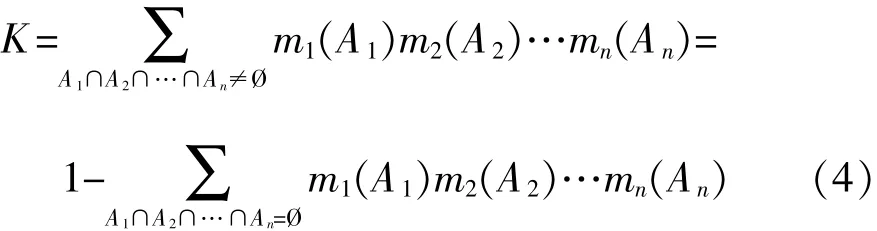
2 构建模糊层次分析模型

荷兰学者Laarhoven[6]提出用三角模糊数获取指标权重排序的计算方法，消除了通过层次分析法获得权重时人为因素影响大的缺陷。之后，基于梯形模糊数、可拓区间数、直觉模糊数等各种形式的模糊层次分析法相继提出。本文就可拓层次分析法进行介绍。

可拓学是由我国学者蔡文创立的一门新学科[7]。可拓层次分析法（extension analytic hierarchy process，EAPH）[8]是在可拓集合理论和方法的基础上建立的一种层次权重决策分析方法。本文考虑复杂度、重要度、MTTR、实现费用、环境条件这5个影响测试性分配因素，建立测试性分配层次结构模型如图1所示。在建立了测试性分配层次结构模型之后，采用可拓层次分析法确定对象层每个LRU的权重。

图1 测试性分配层次结构模型

2.1 层次单排序

这里以对象层和评价层为例，给出求解对象层相对于评价层中某个影响因素权重的流程：

1）聘请多个专家将对象层中所有因素相对于评价层中某个影响因素进行两两比较，用可拓区间数定量表示，从而构造一个可拓区间判断矩阵R，R=（rij）m×n中元素rij=＜r，r＞（i，j=1，2，…，nk）是一个可拓区间数。

2）将判断矩阵R拆成两个矩阵R-和R+，求得这两个矩阵的最大特征值所对应的具有正分量的归一化特征向量x-和x+。

5）采用证据理论将由多个专家评价计算得到的权重向量进行融合，得到融合后的单排序权重向量。

2.2 层次总排序

设第k层包含nk个因素D1，D2，…，Dnk，它们关于k-1层中某一因素G的权重向量为Q=（ω，ω，…，ω）；其下一层k+1包含nk+1个因素（D+1）1，（D+1）2，…，（D+1）nk+1，它们关于第k层中因素Di的权重向量为Q=（ω，ω，…，ω)；那么（D+1）1，（D+1）2，…，（D+1）nk+1

关于G的综合权重也即各组成单元的基础参数为

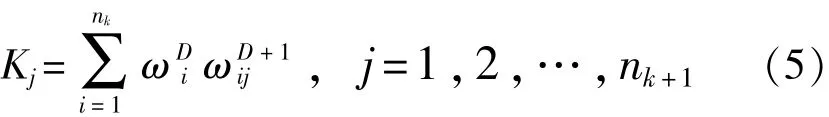
2.3 计算分配额

考虑到系统也具有与各组成单元类似的作为其指针的基础参数Ks，它与各组成单元基础参数Ki的关系为

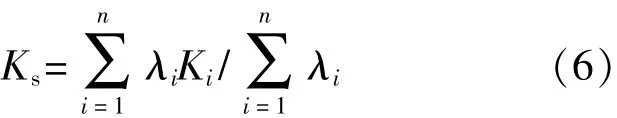
式中λi为第i个组成单元的故障率。

由于各组成单元的测试性指针分配值与其基础参数为正比关系，当知道有关基础参数Ki，并选取Pmax为大于系统测试性要求指针Pr的最大可能实现值后，就可求出各组成单元的分配值P[9]：

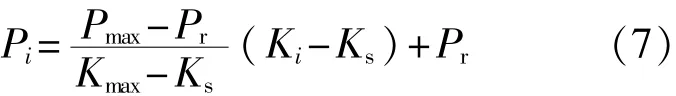
式中Kmax为Pmax对应的最大基础参数。

计算所得Pi值可能会过大或过小，需要调整和修正，过大的可取最大可实现值，过小的可适当提高。再利用：

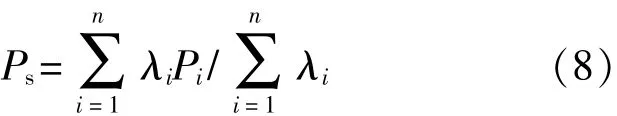
求得系统指针Ps，应保证Ps大于等于系统测试性要求指针Pr，即Ps≥Pr，否则应调整初定分配值。

3 案例应用

以某新研机载电子设备为研究对象，利用上述方法对其进行测试性分配。该设备由5个LRU组成，故障率分别为：λ1=3.5×10-5，λ2=4×10-5，λ3=5.5×10-5，λ4=3×10-5，λ5=4.5×10-5。要求的系统测试性指针（故障检测率）Pr=0.95。聘请3位专家组成专家小组，进行调查问卷，本文采用最适宜于计算准确权值的10/10～18/2标度构造判断矩阵[10-11]。专家根据经验和主观判断，在表格中填写可拓区间数，在得到3位专家的可拓区间数判断矩阵后，利用证据融合算法计算综合可拓区间数判断矩阵。限于篇幅，本文只给出了3位专家关于评价层对目标层的可拓区间数判断矩阵，如表1～表3所示。

由表1中的数据，可得到判断矩阵如下：

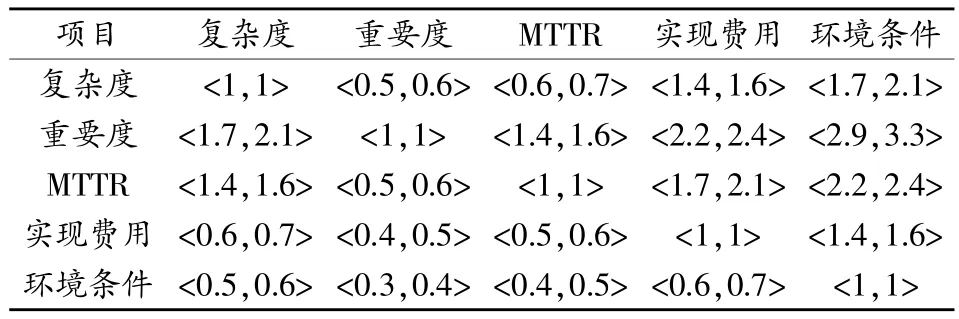
表1 第1位专家关于评价层对目标层的可拓区间数判断矩阵

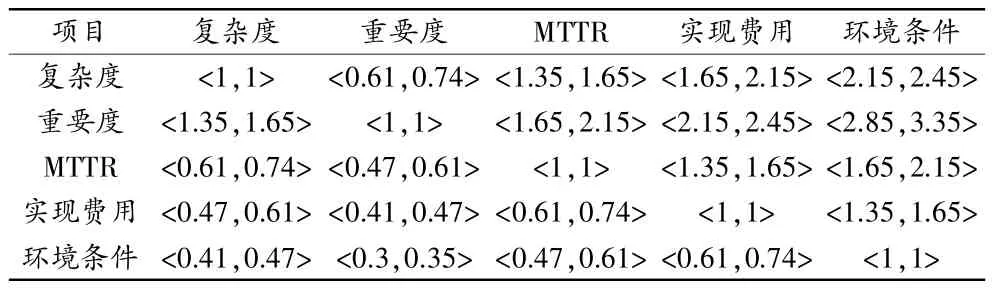
表2 第2位专家关于评价层对目标层的可拓区间数判断矩阵

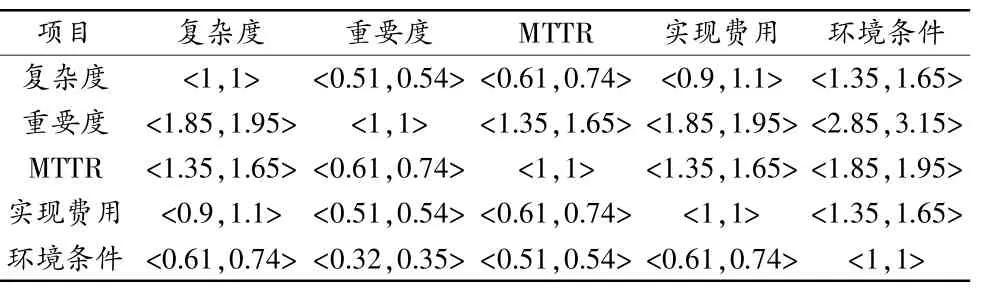
表3 第3位专家关于评价层对目标层的可拓区间数判断矩阵

采用同样的方法可以求得对象层5个LRU对评价层5个评价指标的单排序，在此直接给出计算结果：Q=（0.2437，0.3379，0.296 3，0.088 6，0.0335），Q=（0.245 4，0.181 5，0.066 8，0.187 1，0.315 6），Q= （0.1947，0.0239，0.4713，0.1761，0.134），Q=（0.0419，0.0253，0.0607，0.3841，0.4881），Q=（0.0307，0.0238，0.4375，0.475，0.0329）。由式（5）可计算出各组成单元的基础参数：K1=0.227 8，K2=0.171 2，K3=0.150 7，K4=0.1829，K5=0.2631。由式（6）可以得到系统基础参数Ks=0.1973。选取大于系统测试性要求指标Pr的最大可能实现值Pmax=0.99，由测试性指标分配值与其基础参数成正比可知Kmax=0.205 6，再由式（7）可求出各组成单元的分配值：P1=1.0972，P2=0.8243，P3=0.7253，P4=0.8807，P5=1.267 2。经调整：P1=0.98，P2=0.94，P3=0.92，P4=0.96，P5=0.99。代入式（8）计算得到Ps=0.955 4，大于Pr，各LRU得到了合适的分配指标。

4 结束语

本文首先针对传统测试性分配方法的不足，将可拓层次分析法运用到测试性分配中，并采用最适宜于计算准确权值的10/10～18/2标度构造判断矩阵，该方法考虑了人们判断的模糊性和不确定性，减小了因人为因素带来的误差。其次，运用D-S证据理论来融合不同专家的评价。最后，以某新研机载电子设备为研究对象进行案例应用，针对故障检测率这一指标进行了测试性分配，通过对分析结果的修正，求得了合适的分配指标，结果表明此方法是可行的。

参考文献

[1]田仲，石君友.系统测试性设计分析与验证[M].北京：北京航空航天大学出版社，2003：115-139.

[2]沈亲沐.装备系统级测试性分配技术研究及应用[D].长沙：国防科技大学，2004.

[3]李金龙，陶凤和，贾长治.基于APH的测试性分配方法研究[J].中国测试，2010，36（2）：30-33.

[4]张小红，裴道武，代建华.模糊数学与Rough集理论[M].北京：清华大学出版社，2012：209-221.

[5]田仲.测试性分配方法研究[J].北京：北京航空航天大学学报，1999，25（5）：607-610.

[6] LAARHOVEN V P J M，OEDRYCZ W. A fuzzy extension of satty's priority theory[J]. Fuzzy Set and Systems，1983，11（1）：229-241.

[7]蔡文，杨春燕，林伟初.可拓工程方法[M].北京：科学出版社，1997：56-57.

[8]高洁，盛昭瀚.可拓层次分析法研究[J].系统工程，2002，20 （5）：6-11.

[9] SHAFER G. A mathematical theory of evidence[M]. Princeton：Princeton University Press，1976：139-142.

[10]耿端阳，左洪福，常士基.基于D-S证据融合的民机维修性模糊综合评判[J].航空学报，2006，27（3）：421-426.

[11]徐泽水.关于层次分析法中几种标度的模拟评估[J].系统工程理论与实践，2000（7）：58-62.

（编辑：刘杨）

Study on testability allocation method based on D-S evidence theory

TANG Wenchao1，LI Wenhai1，LUO Tianying2
（1. Naval Aeronautical and Astronautical University，Yantai 264001，China；2. Naval Aeronautical and Astronautical University，Qingdao 266041，China）

Abstract:Fuzzy analytic hierarchy process（AHP）was introduced into testability allocation to solve the deficiency of the existing testability allocation method and the fuzziness and uncertainty of human judgment. First，a single-level sequencing weight vector was obtained and then a total sequencing weight vector，by which the allocation index of each component unit was calculated. The traditional fuzzy AHP has the problem that when integrating the evaluation by multiple experts it just simply adds the evaluation data together and then averages the results. So，D-S evidence theory was used to fuse different experts’conclusions to solve this problem. Ultimately，this method was proved to be feasible in accordance with case application.

Keywords:testability allocation；fuzzy AHP；weight vector；D-S evidence theory

文献标志码：A

文章编号：1674-5124（2016）04-0111-04

doi：10.11857/j.issn.1674-5124.2016.04.024

收稿日期：2015-07-28；收到修改稿日期：2015-09-17

基金项目：总装武器装备预研基金项目

作者简介：汤文超（1989-），男，江苏丹阳市人，硕士研究生，专业方向为电子装备测试性研究。