基于多元非线性回归的刀具几何参数优化

于 金，王胤棋，高彦梁

（沈阳航空航天大学　机电工程学院，沈阳 110136）



基于多元非线性回归的刀具几何参数优化

于 金，王胤棋，高彦梁

（沈阳航空航天大学机电工程学院，沈阳 110136）

摘 要：精密铣削航空接头类薄壁件过程中，硬质合金刀具几何参数（前角、后角和螺旋角）对加工变形有显著影响。采用L25（36）正交实验，运用有限元的方法对25组实验进行铣削加工，获得了变形量与刀具几何参数之间的关系数据，并验证了模型的有效性。运用多元非线性回归技术建立变形量单目标优化数学模型，通过相关性和显著性检验证明模型的可行性。采用遗传算法，以薄壁件的加工变形为目标函数对铣刀几何参数进行优化，最终获得了加工变形量最小时的最优几何参数值。结果表明：所选几何参数与变形量确实有非线性回归关系，且优化后的几何参数组合所对应的变形量比正交实验最小变形量降低了15%。

关键词：薄壁件；精密加工；刀具几何参数；多元非线性回归；遗传算法

0　引言

近年来，许多学者对航空薄壁件加工变形的控制进行了大量深入研究。相比实验研究和分析，有限元仿真模拟技术能节省大量的时间和设备成本，并能够获得实验难以测量的物理力学参数。应用有限元分析技术研究和解决航空薄壁件加工变形问题已成为当前研究的热点和重要手段之一。S. Ratchev［1］等在建立了柔性力学模型的基础上成功实现了对低刚度薄壁件加工变形预测的有限元模拟分析；黄志刚［2］等人运用有限元分析方法，对变形反馈的影响予以简化，分析了航空薄壁框零件的铣削加工变形；浙江大学的董辉跃、柯映林［3］等人对框梁结构件的加工变形进行了研究，并在正交试验的基础上提出了加工变形的预测方法；牛红亮，杜娟［4］等人通过有限元软件模拟了不同切削速度下工件的变形；唐东红、孙厚芳［5］等人利用耦合神经网络的方法建立了工件加工变形的预测模型，并通过遗传算法进行优化，经过验证使加工变形明显得到控制。

以上研究大多集中在铣削参数、装夹力等对加工变形的影响，很少研究刀具几何参数的影响，但在精密数控加工过程中，刀具几何参数对薄壁件的加工变形不容忽视。本文主要针对航空接头类薄壁件，对其铣削过程建立了加工变形的有限元仿真模型，并设计验证性试验证明有限元分析模型的有效性。设计刀具前角、后角和螺旋角的正交实验，得到相关数据，运用多元非线性回归技术建立变形量的单目标优化数学模型，通过相关性检验和线性回归的显著性检验证明模型的可行性。借助遗传算法的全局寻优能力，以变形量预测模型为目标函数，对铣刀几何参数进行优化分析，得到理论最优刀具工艺角度。该方法为合理的选用铣刀以控制薄壁件加工变形提供了有效途径。

1　有限元关键技术和验证性实验

1.1有限元关键技术

在金属切削领域用于描述材料本构关系的理论模型为Johnson-Cook模型。该模型的表达式如式（1）所示［6］：

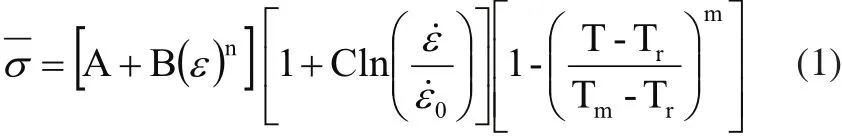
钛合金加工过程中材料的破坏遵循Johnson-Cook动态失效模型，当破坏值大于1时，断裂破坏随之发生［7］。材料破坏的相关参数满足关系式（2）。

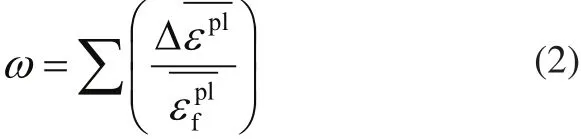
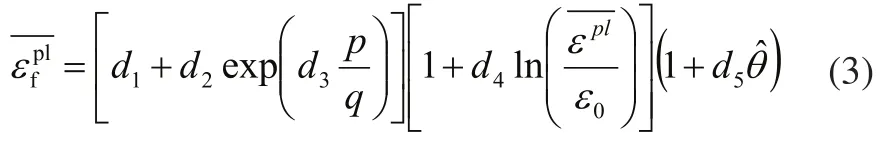
式中：p为压应力；q为VonMises应力；εpl为塑性应变率；ε0为材料的参考应变率；为参考温度25℃；d1～d5为材料常数。

1.2验证性实验

为了验证有限元分析结果的正确性及合理性，本文通过航空接头类薄壁件实际铣削加工进行验证。实验采用XKA714C数控铣床，主轴速度设定为660r/min，每齿进给量设定为0.1mm。工件材料为钛合金TC4，两侧薄壁厚度2mm、底面尺寸长×宽=220mm×20mm，实验采用四齿直柄立铣刀，刀具直径d=10mm，材料为硬质合金YG8。模拟仿真过程各项参数和数据与实验一致，加工现场和有限元模型如图1和图2所示。切削结束后，采用三坐标测量仪AME654对零件关键路径上点的变形进行测量。将试验所测得的Path-X路径和Path-Y路径上各点的变形量数据与仿真值进行比较，得到曲线图如图3中（a）和（b）所示，无论是仿真值的变形大小与变形趋势与实验值都有较好的吻合度从而验证了模型的正确性。

图1　加工现场

图2　有限元模型

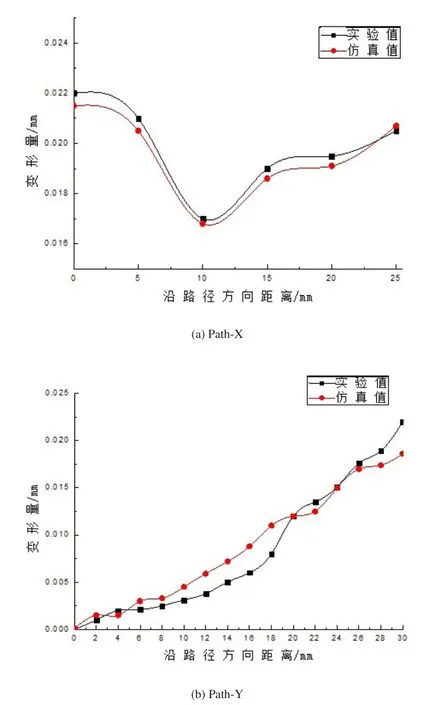
图3　Path-X和Path-Y路径仿真值与实验值比较

2　多元非线性回归模型的建立及验证

2.1实验设计

实验方案采用多元非线性回归正交实验组合设计，研究加工变形与刀具几何参数之间的回归数学模型。正交实验因素数为3，选用L25（36）正交表，试验次数25次，试验中，刀具前角和后角变化范围0°～20°，螺旋角变化范围20°～70°。按照刀具几何参数变化范围对因素水平进行编码，如表1所示。

表1　因素水平编码表

根据上述因素水平值，确定实验方案，采用不同几何参数的直柄立铣刀对工件一侧薄壁进行铣削加工，并测量加工后的变形量。实验方案及结果如表2所示。

2.2回归模型的建立

采用多元非线性回归法，建立变形量与刀具几何参数之间的拟合数学模型。多元二次非线性回归拟合数学关系方程［8，9］为：

式中：y为因变量；β为待定多项式系数：n为设计变量数；xj、xi为自变量。

薄壁件铣削加工模拟实验数据回归分析的自变量有前角x1、后角x2和螺旋角x3，因变量y，样本数据如表2所示。运用MATLAB软件数值计算，最后得到薄壁件变形量与刀具几何参数的多元非线性回归方程：

2.3回归模型的检验

根据多元非线性回归的检验方法，对回归方程进行相关性检验和显著性检验［10，11］。相关性表示自变量与因变量的线性关系，可以用相关系数R来表示他们之间的密切程度：

|R|越接近1，表示自变量与因变量关系越密切，拟合效果越好。通过回归，得出该模型的相关系数为0.9883，非常接近1。因此，可以确定该模型的拟合效果非常好。

对于线性回归的显著性检验，给定显著水平α：

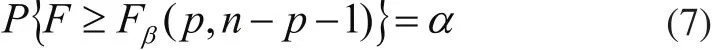
式中：P为概率；F为线性回归显著性检验方法；p为自由度；n为样本数。

回归计算得出F的数值，若：

则认为线性回归显著，本模型经回归后，F值大于从文献［10］查表所得到的F值。因此，可以确定线性回归显著。可见，该数学模型能够精确的反应变形量与刀具几何参数之间的关系。

3　铣刀几何参数优化

本文采用全局寻优能力较强的遗传算法实现对铣刀几何参数的优化，它根据预定的目标函数对个体的适应度进行评价，依据优胜劣汰的进化规则不断的得到更优的群体，同时以全局并行搜索方式来搜索优化群体中的最优个体，以求得最优解［12］。在优化过程中，以控制加工变形最小为目标，根据上述所建立的变形量和铣刀几何参数的模型，相应的优化模型为：

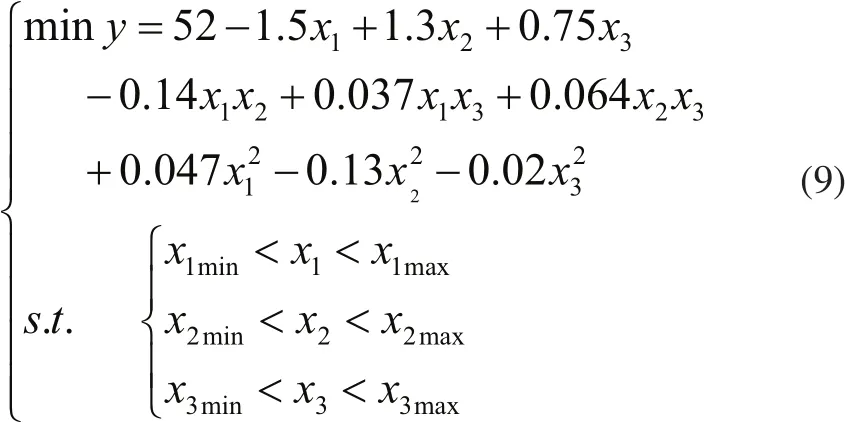
为了获得可能的最优解和较小遗传算法计算量，优化时定义最大遗传代数为M=100，交叉概率Pc=0.2，变异概率Pm=0.05。运用MATLAB进行GA运算，经过迭代最终获得各铣刀角度优化过程的收敛情况如图4所示，其中横坐标是进化代数，纵坐标为目标函数值（适值），即加工变形量。由图看出，随着遗传算法优化的不断进行，加工变形量不断降低。最终获得铣刀各角度的最优结果为：前角x1=6°、后角x2=17°、螺旋角x3=43°，变形量y=34.1μm。在该组铣刀几何参数下进行模拟加工，变形量y=32.9μm，相对误差为3.5%，在允许范围之内，且优于正交实验的最低结果。

【】【】

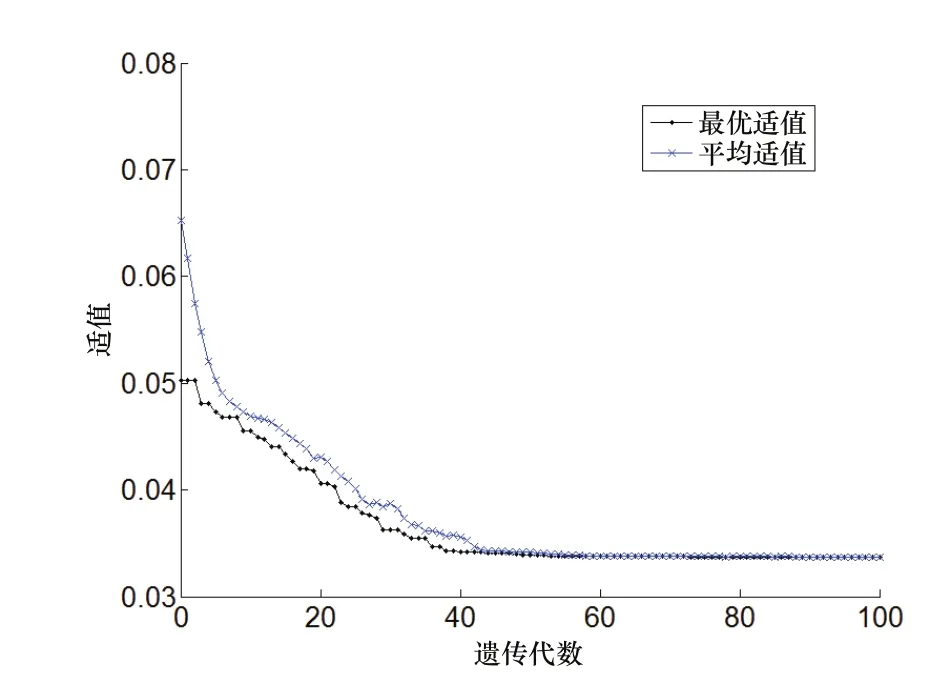
图4　遗传算法迭代结果

4　结论

1）薄壁件铣削加工变形与铣刀几何参数（前角、后角和螺旋角）的数学模型很难确定，本文将多元非线性回归与正交实验相结合确定了其完全二次分布模型，并检验了模型的有效性。

2）在其他加工参数确定的情况下，合理的配置铣刀几何参数，能够有效的控制加工变形。运用遗传算法，得出了铣削该零件的最优铣刀几何参数：前角x1=6°、后角x2=17°、螺旋角x3=43°，使工件的变形量降低到34.1μm，相对于实验结果误差为3.5%，且比正交实验方案变形量最少降低了15%，本文的研究内容为其他复杂刀具的几何参数优化设计提供一定的参考。

参考文献：

［1］ Ratchev.S，Liu，S，Huang.W，et al.A flexible forcemodel for the end milling of low-rigidity parts［J］.Journal of Materials Processing Technology，2004，153-154：134-138.

［2］ 黄志刚.航空整体结构件铣削加工变形的有限元模拟理论及方法研究［D］.杭州：浙江大学，2003.

［3］ 董辉跃，柯映林.铣削加工中薄壁件装夹方案优选的有限元模拟［J］.浙江大学学报，2004，38（1）：17-21.

［4］ 牛红亮，杜娟.薄壁零件高速铣削变形有限元仿真［J］.制造业自动化，2015，37（6）：19-20.

［5］ 唐东红，孙厚芳.基于工件变形控制的铣削参数优化方法研究［J］.中国机械工程，2008，9（19）：1076-1078.

［6］ Johnson G R，Cook W H.A.Constitutive model and data for metals subjected to large strains ，high strain rates and high temperature［A］.Proceedings of the 7th International Symposium on Ballistics.Netherlands［C］.1983：541-547.

［7］ 丁子昀，左敦稳，郭魂，等.多点装夹方案对多框体铣削变形影响的有限元分析［J］.南京航空航天大学学报，2009，41（5）：639-643.

［8］ 张金标，王泾文.热挤压工艺多元非线性回归与多目标优化技术研究［J］.中国机械工程，2010，11（21）：1338-1341.

［9］ 于海莲，王永泉，陈花铃，等.响应面模型与多目标遗传算法相结合的机床立柱参数优化［J］.西安交通大学学报，2012，46（11）：80-85.

［10］ 汪鑫荣.数理统计［M］.西安：西安交通大学出版社，2002.

［11］ Wei S，Nilay P，Rajkumar V，et al.Globle design optimization for aerodynamics and rocket propulsion components［J］.Progress in Aerospace Science，2001，37（1）：59-118.

［12］ 潘永智，艾兴，唐志涛，等，基于切削力预测模型的刀具几何参数和切削参数优化［J］.2008，4（19）：428-431.

Optimization of tool geometry parameters based on multivariate nonlinear regressing

YU Jin， WANG Yin-qi， GAO Yan-liang

中图分类号：TG506.9；TG164

文献标识码：A

文章编号：1009-0134（2016）05-0091-04

收稿日期：2015-11-25

基金项目：辽宁省自然科学基金（2014024006）

作者简介：于金（1961 -），男，大连人，教授，硕士，主要从事数控加工和机电一体化技术的研究等。