巧用类比推理 提高解题能力

刘晓燕

[摘要]在小学数学的教学与研究中，类比是进行合情推理的一种非常重要的思维方法。运用类比推理的方法学习数学，如揭示概念，突出性质，导出公式等，不仅有助于学生发现知识点间的异同，理清知识的来龙去脉，更好地掌握新知，同时，实现了新课程要求的自主学习的目标，便于学生更好地理解、掌握所学知识，提高数学课堂效率。

[关键词]类比推理；揭示概念；突出性质；导出公式；创新解法

所谓类比推理，实际上是根据两个或两类思维对象在某些方面具有的相似点或相同点，进而推理出二者在其它方面具有的相似点或相同点。在小学数学教学中，新旧知识间存在着密切的关联，二者大多有一些相同或相似性。因此，掌握好类比推理这种思维方式，能使学生的逻辑思维能力得到提高，综合应用能力和数学思维得到发展。为此，教师应创设一定的类比情境，将新旧知识之间的相同或相似性展现出来，让学生据此进行类比推理，对提高类比推理能力大有裨益。

一、类比推理，揭示概念

概念教学不仅是小学数学的重要组成部分，也是培养和发展学生数学学习能力的重要内容。概念掌握得不好，不利于判断正误，做题时就容易出错。让学生通过类比的方法对不同的数学概念加以总结和对比，通过分析其异同加深对概念的理解和掌握，有助于帮助学生纠正谬误。

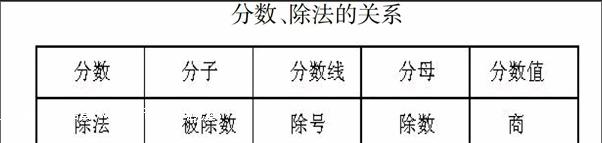
例如：分数的概念是两个正整数p、q相除，可以用分数p/q表示。即p÷q=p/q，其中p为分子，q为分母。为了帮助学生理解这个概念，教师将其与分数与除法之间的异同进行列表比较，突出异同，以便让学生牢记概念。

分数、除法的关系

通过上述类比，学生不但加深了对分数概念的理解，找出它和除法的相似性与差别，也引出了对分数的基本性质的理解，有助于进一步提高解题能力。

二、类比推理，突出性质

引导学生通过将新知识与旧知识进行归类对比，了解数学知识间的内在联系，从而通过已知推测出未知。这样举一反三，融会贯通，将所学的数学知识系统化，有助于发展学生思维的发散性，培养其良好的数学思维和品质。

例如：在学习“比的性质”时，由于比较抽象，学生往往感到晦涩难懂。如何化难为易，变得浅显易懂？教师可以将以前学过的“分数的性质”拿来与其比较。要先让学生做一些练习，重温分数的基本性质：

说出下面各式的商，并说说理由：

280÷40=7

（280×2）÷（40×2）= （280×5）÷（40×5）=

（280÷2）÷（40÷2）= （280÷5）÷（40÷5）=

根据学生的回答，教师板书，然后再引导学生认真观察，比较异同，让学生尝试抽象概括出分数的基本性质，由此得出结论：分数的分子和分母同时乘或者除以相同的数（0除外），分数的大小不变。

在这个过程中，让学生联系比和分数的关系，思考后类比推理“比的基本性质”，学生就能轻而易举地说出，不但复习了旧知，掌握了新知，还实现了知识的迁移，培养了数学学习能力。

三、类比推理，导出公式

新课改要求教师转变传统的教育理念，改变传统的教学模式，创新的教学手段，丰富知识的传授方式。小学数学课程标准提出，要培养学生的动手实践能力，学有用的数学。因此，教师要大胆地放手让学生自己去发现、寻找规律，用自己的所思所想去解决问题。

例如：在“三角形的面积”教学中，在学生已经掌握了平行四边形面积公式的基础上，我交给学生一把剪刀和一个平行四边形的学具，让他们自己尝试导出三角形的面积公式。只见有的学生将平行四边形的对角形一折，用剪刀把它剪成了两个三角形。这时，精彩的对话开始了：

生1：老师，我发现沿平行四边形的其中一条对角线一剪，剪出两个一样的三角形。

生2：老师，我也剪出了两个一样的三角形，那不说明三角形的面积就是平行四边形面积的一半吗？

生3：平行四边形的面积是底×高，用字母表示是S=ah，那三角形的面积就是底×高÷2，用字母表示是S=ah/2。

这种推导公式的方法，既节省了课堂时间，又为以后学习梯形面积公式做了铺垫，达到了小学数学课程标准提出的三维目标要求。

四、类比推理，明晰法则

掌握一定的数学法则或规则，有助于学生将其灵活地运用到实际生活或情境中去解决相应的问题。因此，教师要想方设法让学生经历数学法则或规则的推导过程与结论，掌握不同数学规则之间的关系，明确其异同，熟练掌握它们并灵活地运用。

例如：学习“面积单位间的进率”时，联系前面学过的长度单位，让学生回忆：长度单位是每相邻两个单位间的进率是10，即1米=10分米，1分米=10厘米……那么，每相邻的两个面积单位间的进率是多少？这时，指导学生拿出边长为1分米的正方形学具，先用分米为单位算出此正方形的面积是1平方分米；然后用厘米作单位，算出此正方形的面积是100平方厘米，再用同样的方法推导出1平方厘米=100 平方毫米，从而得出结论：每相邻两个面积单位之间的进率为100。

五、类比推理，创新解法

数学解题能力的培养是一个复杂、漫长的过程。在小学数学教学中，学生解题能力主要体现在对应用题、文字题、计算题等各类问题的处理上。类比不仅是一种从特殊到特殊的推理方法，也是一种探索解题思路、猜测问题答案或结论的一种有效的方法。类比推理法实际上是培养学生的一种发散思维，拓宽学生的解题思路，达到举一反三、触类旁通的效果。这对数学教学中培养学生的创造性思维能力有着极其重要的作用，教学中应引起足够的重视。

在复习百分数应用题时，教师可以联系分数应用题的解题方法，与之作比较，找出它们之间的联系，从而降低学习难度，培养学生灵活运用知识的能力。

例如：在百分数“比多少”一类应用题的结构中，已知条件存在着正、反两种叙述方法。以下题为例：

（1）甲数是120，乙比甲多30%，乙数是多少？

（2）甲数是120，比乙数多30%，乙数是多少？

（3）甲数是120，比乙数少30%，乙数是多少？

（4）甲数是120，乙数比甲数少30%，乙数是多少？

通过读题辨析，学生了解到上述问题中，（1）（3）为正面叙述法，学生比较容易解题，实质相同；（2）（4）为反面叙述，需要逆向思维，实质相同。

这种形式上的比较，可以挖掘其计算本质上的同异，简便解题方法，使学生的思维能力得到提高。

例如：一篇文稿，甲单独打字要10小时完成，乙单独打字要15小时完成。若甲乙两个人合作，几小时可以打完这篇文稿？

在这道关于工作量的应用题中，工作总量可以看作单位“1”，甲的工作效率可以看作1/10，乙的工作效率可以看作1/15，根据工作总量÷工作效率和=工作时间，这题的解法是：1÷（1/10+1/15）。同样的一道行程问题：轿车从甲地开往乙地要5小时，货车从乙地开往甲地要10小时，如果甲乙两车分别从甲、乙两地同时相对开出，几小时可以相遇？在这道行程应用题中，同样可以把总路程看作单位“1”，轿车速度看作1/5，货车速度看作1/10。因此，从上一题的解法可以类推出本题的解法为：1÷（1/5+1/10）。

通过上述类比，可以找到两类不同应用题的共同解法，有利于学生构建数学知识的网络。

总之，类比推理不仅仅是一种推理的方法，更是培养学生发散思维，提高数学能力的良好途径。教师在教学中一定要引导学生 细心观察，认真分析，正确把握类比的对象，确定其在某些特征上具有相同或相似性，然后再有根据地进行类比推理，防止出现偏差，从而有意识地培养和强化小学生的类比思维能力，增强其数学学习的主动性和积极性。

参考文献：

[1]王彦兰.小学数学思维方法论[M].吉林：吉林人民出版社，1990.

[2]顾冷沅.数学思想方法[M].北京：中央广播电视大学出版社，2004.

[3]张雨宇.类比法在小学数学教学中的几点运用[J].教学研究，2009.

（责任编辑 付淑霞）endprint