常见递推数列通项公式的求解方法

王新宏

(甘肃省张掖市实验中学，734000)



常见递推数列通项公式的求解方法

王新宏

(甘肃省张掖市实验中学，734000)

数列是高中数学的一项重点内容,求递推数列的通项是其中的一个难点.它类型多,解法灵活,技巧性强,是考查学生逻辑推理与化归转化能力的良好载体,也是近年来高考常有的内容.下面介绍高中阶段四种常见递推数列通项公式的求解方法,希望对读者能有所启发与帮助．

一、累加法

它适用于在数列{an}中,已知首项a1,且满足an+1=an+f(n),其中数列{f(n)}是可以求和的.通常f(n)有以下三种常见类型:

(1)f(n)=kn+b(k≠0),那么数列{f(n)}为等差数列,其中k为公差,首项为k+b;

(2)f(n)=kan(ak≠0,a≠1),那么数列{f(n)}为等比数列,其中a为公比,首项为ka;

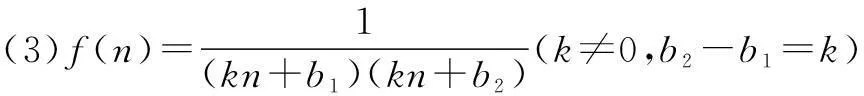
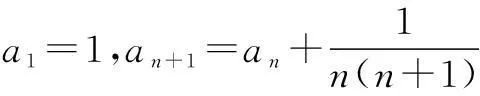
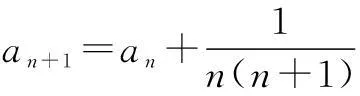
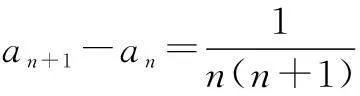
结合已知，得

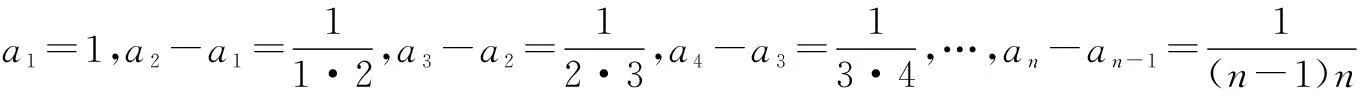
以上n个等式相加，得

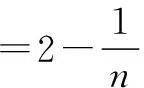
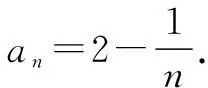
巩固练习1

(1) 已知数列{an}满足a1=1,an+1=an+3n,求数列{an}的通项公式．

(2) 已知数列{an}满足a1=1,an+1=an+2n+1,求数列{an}的通项公式．

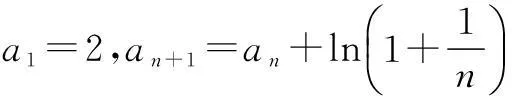
二、累积法

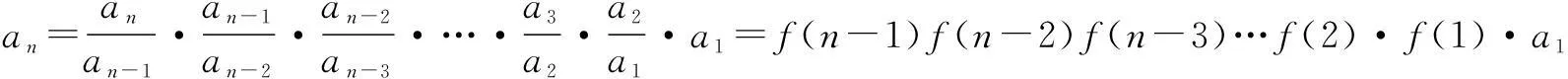
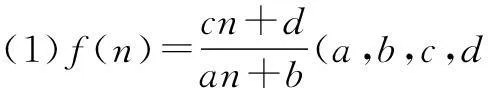
(2)f(n)=kan,(ak≠0,a≠1),即数列{f(n)}为等比数列,其中a为公比,首项为ka.

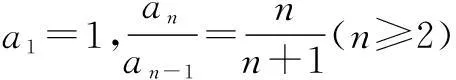
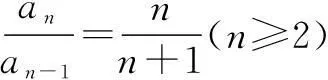
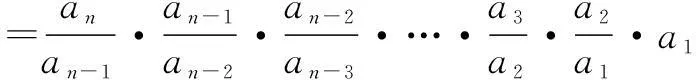
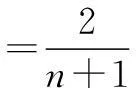
注意:累积法求通项共有的一步是

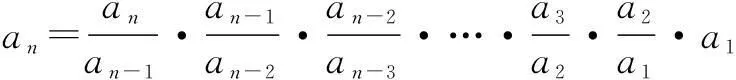
巩固练习2

在数列{an}中,已知a1=1,an+1=2n·an,求数列{an}的通项公式.

三、构造等差数列法

这里我们主要介绍最简单,最为常见的构造出新的等差数列的三种类型,

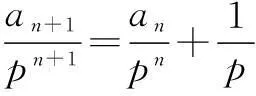
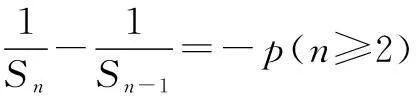
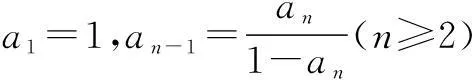
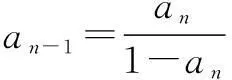
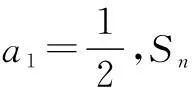
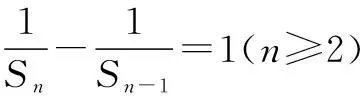
因为an=-SnSn-1(n≥2),所以

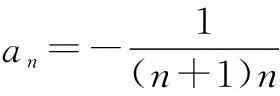
巩固练习3

在数列{an}中,已知a1=2,an+1=2an+2n+1,求数列{an}的通项公式.

四、构造等比数列法

这种方法主要适用于以下五种常见类型:

(1)在数列{an}中,已知首项a1,且满足an+1=pan+q(p,q为常数,且p≠0,且p≠1).此类数列解决的思路是运用化归与转化的思想,利用待定系数法或作差法,构造新的等比数列求解.

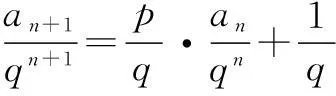
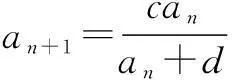
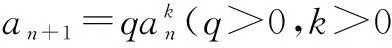
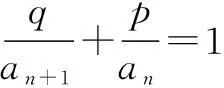
例5在数列{an}中,已知a1=1,当n≥2时,有an=3an-1+2,求数列{an}的通项公式.

分析1(待定系数法)

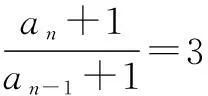
分析2(作差法)

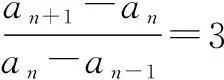
例6在数列{an}中,已知a1=1,an+1=3an+2n+1,求数列{an}的通项公式.

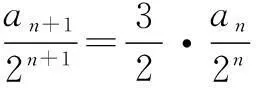
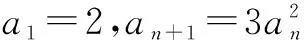
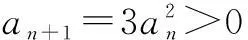
(本文为甘肃省教育科学“十二五”规划2013年度《新课改理念下高三数学复习高效策略研究》课题(课题批准号GS(2013)GHB0771)成果之一．)

○解题思路与方法○