气浮接触区气泡聚并行为的数值模拟

陈阿强，王振波，王晨，杨佳佳，金有海（中国石油大学（华东）重质油国家重点实验室，山东 青岛 266580）



气浮接触区气泡聚并行为的数值模拟

陈阿强，王振波，王晨，杨佳佳，金有海
（中国石油大学（华东）重质油国家重点实验室，山东 青岛 266580）

摘要：在气浮接触区内，聚并会导致气泡直径增大，对分离效果产生影响。采用相群平衡模型对接触区气泡聚并行为进行数值模拟，研究了气泡聚并发生的原因及来液流量、回流流量对气泡聚并的影响。首先分别应用Schiller-Naumann、Grace和Tomiyama 3种曳力系数模型进行模拟，所得气泡直径均与实验值吻合，无明显差异，选定Schiller-Naumann曳力系数模型对气浮中两相流动进行模拟。通过对模拟结果进行分析，表明回流入口周围上下行流过渡区域存在较大速度梯度，是导致气泡聚并的关键因素。最后研究了来液流量和回流流量对接触区气泡尺寸的影响，接触区上部气泡直径随回流流量增大而明显增大，原因在于增大回流流量使得过渡区域速度梯度升高，气泡聚并频率提高；而来液流量对气泡尺寸基本无影响。

关键词：气浮；气泡；聚并；速度梯度；相群平衡模型；数值模拟；计算流体力学

2015-11-04收到初稿，2016-01-20收到修改稿。

联系人：王振波。第一作者：陈阿强（1988—），男，博士研究生。

Received date: 2015-11-04.

Foundation item: supported by the Fundamental Research Funds for the Central Universities (14CX06097A).

引　言

气浮分离技术对微小颗粒及油滴具有良好的分离效果，被应用于饮用水净化及污水处理等多个领域[1-3]。气浮装置形式多样，且不断有新型气浮装置被开发出来[4-5]，其中溶气气浮应用最为广泛。在高压溶气罐内，水与空气混合形成溶气水，经释放头形成微气泡，颗粒或油滴与气泡发生黏附形成絮团，上浮至水面后被刮除，完成分离过程。在此过程中，气泡作为一种关键媒介强化了浮选分离过程，其直径分布对分离效果有重要影响[6-8]。

研究者采用图像分析、颗粒计数及激光衍射等方法对气浮中气泡尺寸进行了测量，重点关注溶气法生成气泡尺寸及其影响因素。生成气泡尺寸主要受到溶气压力和表面活性剂种类浓度的影响。随溶气压力升高，气泡直径先减小，达到临界压力（0.4 MPa左右）后，不再发生变化[9-11]。向水中加入表面活性剂有助于减小生成气泡直径及临界压力[12-13]。气浮池中，气泡尺寸除受以上因素影响外，聚并同样会对接触区气泡尺寸分布产生影响[14]，但目前对该方面的研究十分有限。Couto等[15]用溶气法生成气泡，分别注入含表面活性剂的水及清水中，发现加入表面活性剂后气泡直径减小。该实验间接证明气泡聚并的存在及其对气泡直径的影响。另外，目前几种气泡直径测量方法均需使用引流管将气泡引入观察室或样品池，受到引流管尺寸的影响，测得的不同位置气泡直径实际代表的是某一区域气泡平均直径，即现有测量手段尚无法给出局部气泡尺寸分布情况，也就无法分析接触区各个位置气泡尺寸变化规律，给气泡聚并研究造成困难。

总之，气浮接触区气泡聚并尚待进一步研究，但目前的测量方法难以提供必要的气泡直径分布数据。而数值模拟可以计算得到流动区域的全流场信息，且相群平衡模型提供了一种有效的研究聚并的方法，在鼓泡塔等的模拟中得到应用，模拟结果与实验吻合较好。因此本文拟采用相群平衡模型对不同条件下气浮接触区气泡尺寸分布进行数值模拟，通过对结果进行分析探究造成气泡聚并的原因及影响因素，为实际应用中气泡尺寸控制提供指导。

1　数学模型及数值模拟方法

1.1几何模型与网格划分

图1　气浮接触区模型及网格划分Fig. 1　Model and mesh of contact zone of dissolved air flotation cell

图1所示为模拟所用气浮接触区流域模型及网格。实际接触区流域如图1(a) 虚线左侧所示，模拟时为保证出口流动充分发展，对出口适当延长（extended part）。根据Babaahmadi[16]的研究，延长接触区出口有助于提高模拟准确性。完成建模后用ICEM划分网格，结果如图1(b) 所示。为提高计算效率，空间离散采用结构化网格。另外，对回流（recycle flow）入口及壁面网格分别进行加密。根据网格无关性验证[17]，应用5 mm网格和4 mm网格进行模拟时，得到的接触区气泡尺寸随高度变化相同，网格尺寸为6 mm时计算结果产生差异，所以最终确定网格尺寸为5 mm。为准确描述回流入口处流动状态及气泡行为，对该处进行局部加密，近壁面网格厚度设为0.8 mm，接触区网格总数为260648个。

1.2控制方程

1.2.1连续性方程及动量守恒方程气浮中气泡/水两相无质量传递，第q相质量及动量守恒方程为

式中，ρq为第q相的密度，vq为第q相的速度，∇P为压力梯度，为应力张量， αqρqg为重力项，其中g为重力加速度，Fvm,q为虚拟质量力，为相间作用力。

1.2.2曳力系数模型曳力函数的表达式如下

Schiller-Naumann、Grace和Tomiyama 3种曳力模型曳力系数表达式见表1。Schiller-Naumann模型根据相对Reynolds数不同，分段求得曳力，确定相间作用，作为Fluent软件平台中默认的曳力系数模型，普遍应用于液液两相流动体系。Grace与Tomiyama模型更多应用于气液两相流动的模拟，虽然表达式略有差异，但这两种模型均考虑了气泡形状对气液间作用的影响，对变形气泡流动的模拟较Schiller-Naumann模型更为准确。

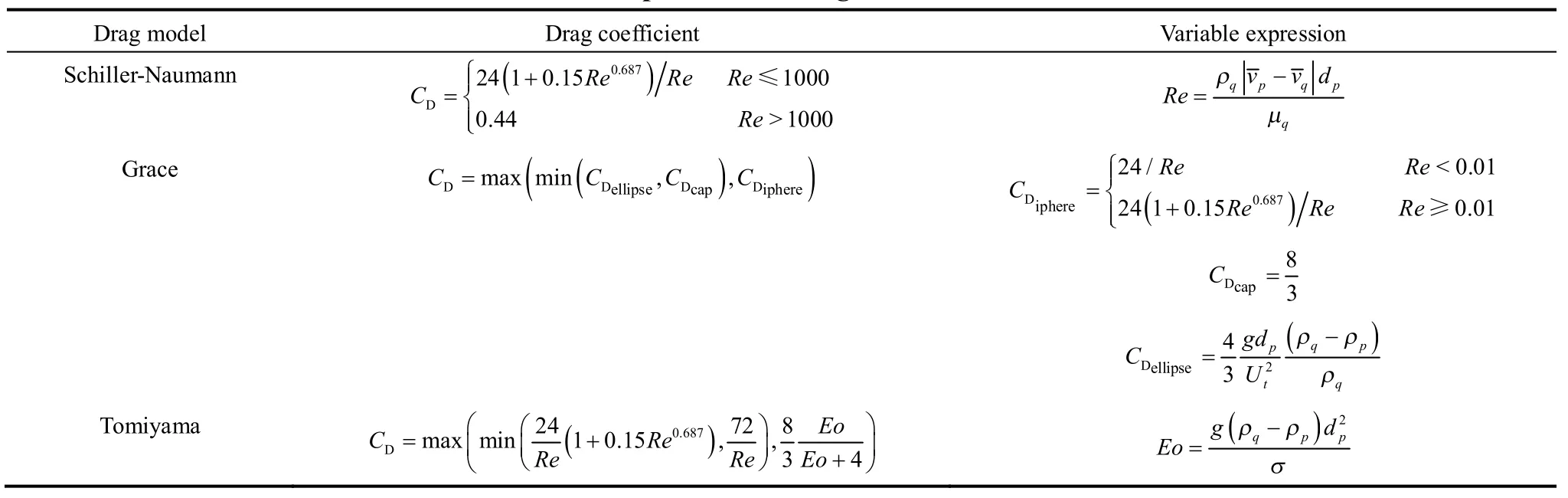
表1　曳力系数模型表达式Table 1　Expressions of drag coefficient models

1.2.3相群平衡模型本研究采用相群平衡模型模拟接触区气泡聚并，使用Turbulent聚并模型确定是否发生聚并。由于气浮池内气泡较小，发生破碎频率极小，因此只考虑聚并过程。

根据Turbulent聚并模型，气泡聚并是由黏性和惯性两种机制引发的。黏性机制下，气泡聚并概率表达式为

式中，ςT为捕获效率系数，γ&为剪切率。惯性机制下，气泡聚并概率表达式为

式中，U2i为i气泡的速度平方均值。

1.3求解方法及边界条件

采用欧拉双流体模型对接触区两相流动进行模拟。相较k-ω及RSM湍流模型，Realizable k-ω模型计算量更小，且能够准确描述气浮湍流状态[18]。根据Bondelind等[19]的研究，应用Realizable k-ω和SST k-ω湍流模型模拟结果基本相同，因此本研究选择Realizable k-ω模型对湍流状态进行计算。为提高计算精度，各变量均采用QUICK格式进行离散。压力速度耦合采用Phase Coupled SIMPLE算法。操作条件不变，气浮接触区流动处于稳定状态，由于稳态计算收敛难度大，因此采用瞬态求解器进行求解，时间步长设为0.002 s，根据前期研究[17]，确定模拟的流动时间大于接触区两倍水力停留时间，以保证达到最终稳态。

来液入口（mainstream flow inlet）及回流入口（recycle flow inlet）均采用速度入口边界，回流入口气泡体积分数根据实验所测空气/水流量比求得，设为0.0385。气泡根据直径分组，各组体积分数见表2。出口为压力出口，壁面采用无滑移壁面条件。接触区上表面为水面，模拟时设为Symmetry边界条件，保证该面处无垂直方向速度分量且壁面摩擦为零。另外在该表面相邻网格应用udf增加质量源项，描述气泡溢出过程。

表2　回流入口气泡直径分布Table 2　Bubble size distribution of recycle flow inlet

2　气泡直径分布的实验测量

气浮实验流程及气泡直径测量装置如图2所示。回流水和空气分别经回流水泵4（recycle flow pump）和空压机5（air compressor）进入溶气罐2 （saturator），空气溶解至水中，形成饱和溶气水。饱和溶气水在释放头10（needle valves）处压力降低，空气成核析出形成微气泡。回流水与来液在接触区混合，气泡发生聚并，平均直径发生改变。

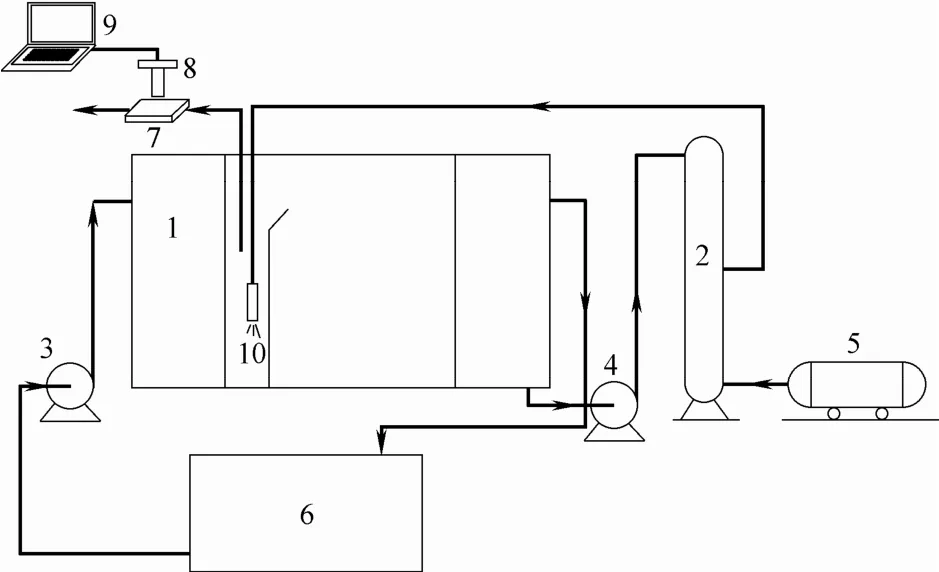
图2　气浮实验装置Fig.2　Schematic diagram of air flotation apparatus1—air flotation tank；2—saturator；3—water pump；4—recycle flow pump；5—air compressor；6—water tank；7—sample cell；8—microscope；9—computer；10—needle valves

为测量接触区不同高度气泡直径分布，根据Rodrigues等[20]和Matiolo等[21]的方法建立了基于显微图像分析的气泡直径测量方法。测量时首先将气泡引入样品槽7（sample cell），通过显微镜8 （microscope）放大并用计算机9（computer）采集图像，后采用Matlab软件对图像进行批量处理，得到气泡直径分布。为保证测量结果的准确性，单个测点所测气泡数不少于500个。前期研究中给出了实验测量图像及接触区不同高度气泡Sauter平均直径[17]，在此不再赘述。

3　数值模拟结果及讨论

3.1曳力系数选择及数值方法验证

进行气泡/水两相流动模拟时，选择合适的曳力模型是必要的。首先分别对Schiller-Naumann、Grace、Tomiyama 3种曳力模型进行考察。来液流量和回流流量分别为600 L·h−1和300 L·h−1，回流入口气泡直径如表2所示，平均值78.7 μm。模拟所得z=300 mm高度截面气泡平均直径分布如表3所示。基于3种曳力模型计算得到300 mm高度处气泡平均直径分别为105.76、105.77、106.87 µm，基本相同，且与实验值吻合较好，说明所采用数值模拟方法准确可行。

表3　实验及数值模拟气泡平均直径变化Table 3　Bubble diameter change produced by experiments and numerical simulation/µm

采用不同曳力模型模拟所得z=300 mm截面x方向气含率分布如图3所示。3种曳力模型下，气含率分布呈相同趋势，由边壁（x=0）至回流入口管壁（x=35 mm），气含率逐渐升高。3种曳力模型计算所得各个位置处的气含率值基本相同。

图3　曳力模型对z=300 mm截面x方向气含率分布的影响Fig.3　Influence of drag models on air volume fraction along x direction

综上所述，采用Schiller-Naumann(S-N)、Grace、Tomiyama 3种曳力模型模拟结果相同。但在鼓泡塔气液流动模拟中，曳力系数对两相流动有明显影响[22-23]。与Schiller-Naumann模型相比，Tomiyama曳力模型对鼓泡塔中气相体积分数分布的预测与实验值更接近。两种工艺过程的重要区别在于气泡直径的差异。为分析气泡直径对曳力系数的影响，对不同模型曳力系数与气泡直径的关系进行对比。由于Grace与Tomiyama模型的基本假设及理论相似，仅选Tomiyama模型与Schiller-Naumann模型进行对比。Re分别为100和1000时，Schiller-Naumann 和Tomiyama曳力模型计算得曳力系数与气泡直径的关系如图4所示。Schiller-Naumann未考虑气泡直径对曳力的影响，随直径增大，曳力系数不发生改变。随气泡直径增大，Tomiyama模型求得曳力系数增大，呈现与Schiller-Naumann模型不同趋势。但在气泡直径小于1000 µm时，曳力系数基本不随气泡直径发生改变，且其数值与Schiller-Naumann的预测值相近。气浮接触区气泡直径通常小于150 µm，故不同曳力系数算得气泡直径及气含率分布相同，而对鼓泡塔，由于存在直径较大气泡，Tomiyama 和Grace模型表现出比Schiller-Naumann模型更高的准确性。

图4　气泡直径对曳力系数影响Fig.4　Influence of bubble diameter on drag coefficient

Schiller-Naumann比Tomiyama和Grace曳力模型计算过程更简单，模拟结果无明显差别，所以采用Schiller-Naumann模型进行计算。

3.2气泡聚并行为分析

为分析接触区气泡聚并发生区域及原因，选取y方向中心截面即y=175 mm截面进行分析，图5所示为该截面气泡直径分布。由图可见，中心回流管附近气泡直径较大，靠近边壁气泡直径变小，这是由于回流管壁附近气含率更高，相应地，气泡数密度较大，气泡聚并频率更高，气泡直径较边壁处更大。向上流动过程中，气泡直径有所增大。回流水入口下方区域，气泡直径未发生明显改变，保持在80 μm左右。而该流动区域外侧气泡直径明显增大，达到110 μm，说明该处气泡聚并频率较高。气泡聚并与流动状态密切相关，作y=175 mm截面速度矢量图（图6）进行对比分析，发现气泡直径较大的区域位于上行流与下行流过渡区域，该处存在较大速度梯度。

图5　y=175 mm截面气泡直径分布Fig.5　Bubble diameter distribution at plane y=175 mm

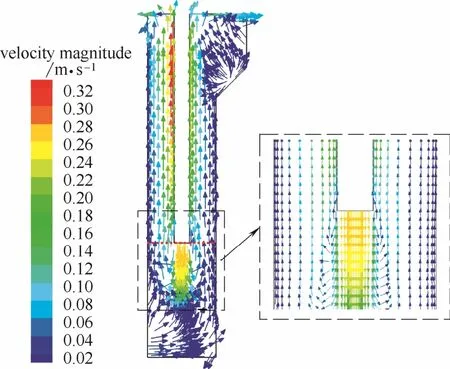
图6　y=175 mm截面速度矢量图Fig.6　Velocity vectors at plane y=175 mm

为分析气泡直径与速度分布之间的关系，计算回流入口平面沿x方向（图5、图6中红色虚线所示）气泡直径和速度梯度分布，结果如图7所示。该流动区域速度主要沿垂直方向，z向速度分量远大于x和y方向速度分量，计算时以z向速度代替速度值，第n个网格处速度梯度Ln求解式为

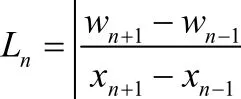
式中，wn+1和wn−1分别为相邻网格的z向速度，xn+1和xn−1分别为相邻网格的x方向位置坐标。由图可见，x=40～50 mm区域即回流入口区域，速度梯度为0，气泡直径保持在78.7 μm，未发生聚并。回流入口周边区域（x=30～40 mm与x=50～60 mm），速度梯度明显增大，气泡直径出现最大值。靠近壁面处（x=0～20 mm与x=70～90 mm）速度梯度较小，气泡直径较入口区域有所增大，小于回流入口周边区域。沿x方向，气泡尺寸与速度梯度分布呈现相同趋势。由于没有考虑成核及压力导致的气泡体积变化，接触区气泡尺寸变化由聚并导致。根据Friedlander[24]和Williams等[25]的研究，速度梯度会诱导颗粒碰撞，与模拟结果一致。所以回流与周围流体间的速度梯度是导致气浮中气泡聚并的关键因素。

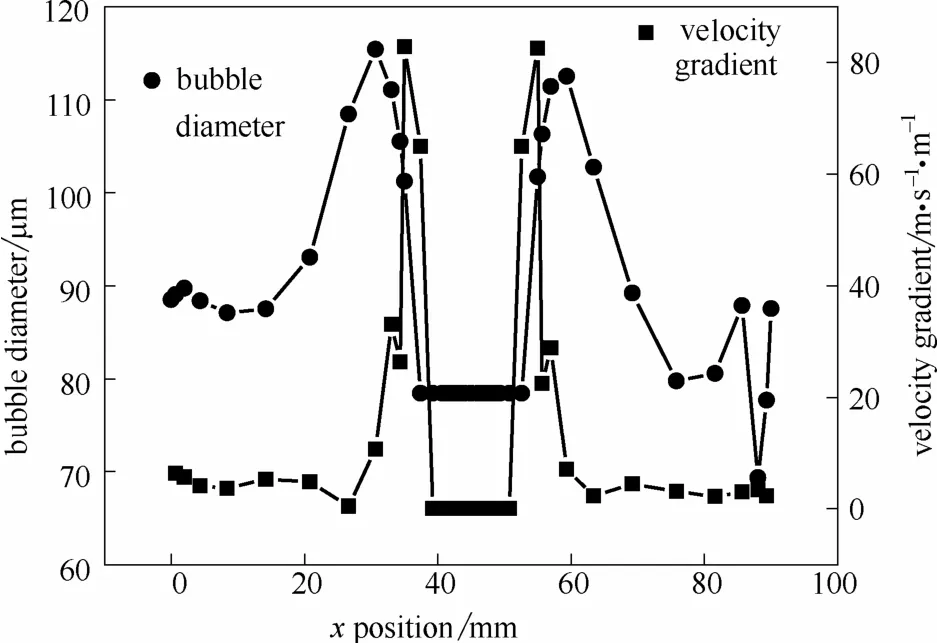
图7　回流水入口处x方向气泡直径及速度梯度分布Fig.7　Bubble diameter and velocity gradient along x direction of inlet of recycle flow

3.3流量对气泡聚并影响

来液流量与回流水流量是气浮中两个重要操作参数，其对接触区气泡尺寸的影响如图8所示。图中z=300 mm高度平面气泡Sauter平均直径代表气泡聚并完成后的最终直径。来液流量保持600 L·h−1不变，回流水流量由100 L·h−1增大至500 L·h−1，最终气泡直径由85 μm增大至131 μm。回流水流量保持300 L·h−1不变，来液流量由400 L·h−1增大至800 L·h−1，气泡直径均为104 μm左右，未发生明显改变。由此，回流流量对接触区气泡聚并影响显著，而来液流量对气泡聚并基本无影响。

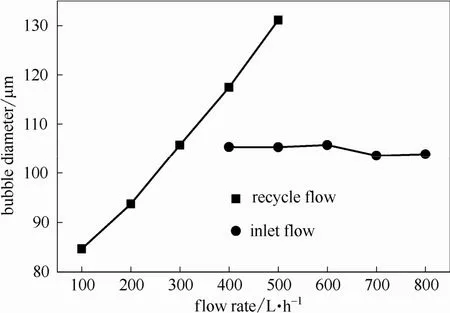
图8　不同入口及回流流量下接触区z=300 mm截面气泡平均直径Fig.8　Mean bubble diameter of plane z=300 mm of contact zone under various inlet and recycle flow rate

对不同操作条件下回流入口平面（z=150 mm）沿x方向气泡直径及速度梯度进行比较。不同回流流量下气泡直径及速度梯度分布分别如图9、图10所示。由图9可见气泡直径在不同回流流量下的分布趋势相似，最大值均位于回流周围区域。随回流流量增大，气泡直径增大。速度梯度在相同区域存在最大值，且最大速度梯度同样随流量增大而增大（图10）。与回流流量的影响不同，来液流量由200 L·h−1增大至500 L·h−1，速度梯度和气泡直径均未发生明显变化（图11、图12），说明来液流量变化对气浮接触区气泡聚并基本无影响。由此，回流流量增大导致速度梯度明显提高，加剧气泡聚并程度，进而导致气泡直径增大；来液流量大小对速度梯度影响不明显，气泡聚并程度无变化，气泡直径保持不变。以上模拟结果同样证明速度梯度对气泡聚并有重要影响。实际应用中，在保证气含率满足要求的情况下，应该考虑通过合理的回流入口结构设计及空间布置减小回流入口周围速度梯度，以控制气泡聚并程度，保证气泡尺寸满足浮选分离要求。而来液流量对聚并影响较小，可不作为主要控制因素。

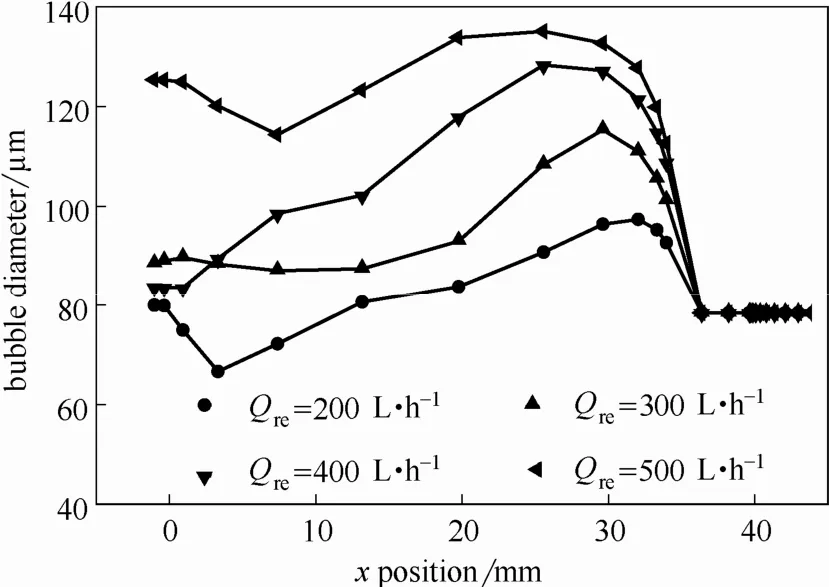
图9　不同回流流量下回流入口平面气泡直径分布Fig. 9　Bubble size distribution of recycle flow inlet plane under various recycle flow rates

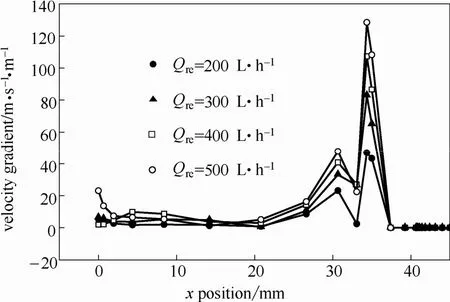
图10　不同回流流量下回流入口平面速度梯度分布Fig.10　Velocity gradient distribution of recycle flow inlet plane under various recycle flow rates

图11　不同入口流量下回流入口平面气泡直径分布Fig.11　Bubble size distribution of recycle flow inlet plane under various inlet flow rates

图12　不同入口流量下回流入口平面速度梯度分布Fig.12　Velocity gradient distribution of recycle flow inlet plane under various inlet flow rates

4　结　论

基于相群平衡模型，采用数值模拟方法对气浮接触区中气泡聚并行为进行研究，通过对气泡直径、气含率和速度分布进行分析，得到以下结论。

（1）气浮接触区两相流动模拟中，应用Schiller-Naumann、Grace和Tomiyama 3种曳力模型模拟所得结果无差异，原因在于气浮中气泡直径较小，变形可忽略，根据3种模拟计算得到的曳力系数相近。

（2）速度梯度与气泡直径分布呈相同趋势，回流水入口周围上行流与下行流过渡区域存在较大速度梯度，是导致接触区气泡聚并的关键因素。

（3）相较来液流量，回流流量对气泡聚并影响更明显。增大回流流量使回流入口周围区域速度梯度明显增大，气泡聚并加剧，气泡直径相应增大；来液流量对速度梯度无影响，气泡最终直径不发生改变。

符号说明

CD——曳力系数

L——速度梯度，m·s−1·m−1

Re——Reynolds数

w——z向速度，m·s−1

x——x方向位置，mm

y——y方向位置，mm

z——z方向位置，mm

φ——回流管直径，mm

References

[1]KOIVUNEN J, HEINONEN-TANSKI H. Dissolved air flotation (DAF) for primary and tertiary treatment of municipal wastewaters [J]. Environ. Technol., 2008, 29(1): 101-109.

[2]KARAGUZEL C. Selective separation of fine albite from feldspathic slime containing colored minerals (Fe-Min) by batch scale dissolved air flotation (DAF) [J]. Miner. Eng., 2010, 23(1): 17-24.

[3]WANG H, CHEN X L,BAI Y, et al. Application of dissolved air flotation on separation of waste plastics ABS and PS [J]. Waste Manag., 2012, 32(7): 1297-1305.

[4]王新海, 郑伟, 马骏, 等. 基于高溶气量的新型气浮系统的性能[J]. 化工学报, 2013, 64(3): 1099-1105. WANG X H, ZHENG W, MA J, et al. Performance of new flotation system based on high dissolved air content [J]. CIESC Journal, 2013, 64(3): 1099-1105.

[5]蔡宏镇, 沈忱, 任满年, 等. 环流气浮法处理含油水体工艺 [J].化工学报, 2015, 66(2): 605-611. CAI H Z, SHEN C, REN M N, et al. Loop flotation for oil-containing water treatment [J]. CIESC Journal, 2015, 66(2): 605-611.

[6]LEPPINEN D, DALZIEL S. Bubble size distribution in dissolved air flotation tanks [J]. Journal of Water Supply: Research & Technology-AQUA, 2004, 53(8): 531-543.

[7]BYEONG-YONG S, SOON-BUHM K, JIN-HEE M, et al. Characteristics of pretreatment parameters and bubble size influencing DAF efficiency [J]. Separation Science & Technology, 2009, 44(9): 1941-1953.

[8]LAKGHOMI B, LAWRYSHYN Y, HOFMANN R. A model of particle removal in a dissolved air flotation tank: importance of stratified flow and bubble size [J]. Water Research, 2015, 68:262-272.

[9]ZHANG W, ZHANG J, ZHAO B, et al. Microbubble size distribution measurement in a DAF system [J]. Industrial & Engineering Chemistry Research, 2015, 54: 5179-5183.

[10]HAN M, PARK Y, LEE J, et al. Effect of pressure on bubble size in dissolved air flotation [J]. Water Science & Technology Water Supply, 2002, 2(5): 41-46.

[11]VLYSSIDES A, MAI S, BARAMPOUTI E. Bubble size distribution formed by depressurizing air-saturated water [J]. Industrial & Engineering Chemistry Research, 2004, 43(11): 2775-2780.

[12]FERIS L, GALLINA C, RODRIGUES R, et al. Optimizing dissolved air flotation design and saturation [J]. Water Science & Technology, 2001, 43(8): 145-152.

[13]PÉREZ-GARIBAY R, MARTÍNEZ-RAMOS E, RUBIO J. Gas dispersion measurements in microbubble flotation systems [J]. Minerals Engineering, 2012, 26(1): 34-40.

[14]EDZWALD J. Dissolved air flotation and me [J]. Water Research, 2010, 44(7): 2077-2106.

[15]COUTO H, NUNES D, NEUMANN R, et al. Micro-bubble size distribution measurements by laser diffraction technique [J]. Miner. Eng., 2009, 22: 330-335.

[16]BABAAHMADI A. Numerical investigation of the contact zone on geometry, multiphase flow and needle valves[D]. Göteborg: Chalmers University of Technology, 2010.

[17]陈阿强, 王振波, 孙治谦. 基于相群平衡模型的浮选气泡聚并模拟 [J]. 化工学报, 2015, 66(12): 4780-4787. CHEN A Q, WANG Z B, SUN Z Q. Numerical simulation of bubble coalescence in dissolved air flotation tank based on population balance model [J]. CIESC Journal, 2015, 66(12): 4780-4787.

[18]BONDELIND M, SASIC S, KOSTOGLOU M, et al. Single- and two-phase numerical models of dissolved air flotation: comparison of 2D and 3D simulations [J]. Colloids & Surfaces A Physicochemical & Engineering Aspects, 2010, 365(1/2/3): 137-144.

[19]BONDELIND M, SASIC S, PETTERSSON T J R, et al. Setting up a numerical model of a DAF tank: turbulence, geometry, and bubble size [J]. Journal of Environmental Engineering, 2010, 136(12): 1424-1434.

[20]RODRIGUES R, RUBIO J. New basis for measuring the size distribution of bubbles [J]. Miner. Eng., 2003, 16(8): 757-765.

[21]MATIOLO E, TESTA F, YIANATOS J, et al. On the gas dispersion measurements in the collection zone of flotation columns [J]. Int. J. Miner. Process,2011, 99(1/2/3/4): 78-83.

[22]吴宗应, 杨宁. 曳力模型对模拟鼓泡塔气含率的影响 [J]. 化工学报, 2010, 61(11): 2817-2822. WU Z Y, YANG N. Effect of drag models on simulation of gas hold-up in bubble columns [J]. CIESC Journal, 2010, 61(11): 2817-2822.

[23]李孟, 李向阳, 王宏智, 等. 鼓泡塔气液两相流不同曳力模型的数值模拟 [J]. 过程工程学报, 2015, 15(2): 181-189. LI M, LI X Y, WANG H Z, et al. Numerical simulation of gas-liquid two-phase flow in a bubble column with various drag models [J]. The Chinese Journal of Processing Engineering, 2015, 15(2): 181-189.

[24]FRIEDLANDER S K. Smoke, Dust and Haze. Fundamentals of Aerosol Behavior[M]. New York: John Wiley, 1977.

[25]WILLIAMS M M R, LOYALKA S K. Aerosol Science Theory and Practice: with Special Applications to the Nuclear Industry[M]. Oxford: Pergamon Press, 1991.

Numerical simulation of bubble coalescence behavior in contact zone of dissolved air flotation tank

CHEN Aqiang, WANG Zhenbo, WANG Chen, YANG Jiajia, JIN Youhai
（State Key Laboratory of Heavy Oil, China University of Petroleum, Qingdao 266580, Shandong, China）

Abstract:Bubble coalescence can make the increase of bubble size in the contact zone of the dissolved air flotation tank, which will finally influence the separation efficiency. Population balance model was employed to study bubble coalescence behavior in the contact zone. With this numerical method, the bubble coalescence mechanism and effect of mainstream and recycle flow rates on coalescence phenomenon were studied. At first, Schiller-Naumann, Grace and Tomiyama drag coefficient models were included in the simulation process, respectively. The results showed that the bubble sizes simulated with these three models were similar with good accordance with the experimental data. Schiller-Naumann was adopted in the following simulation as its computational cost was lower than Grace and Tomiyama model. By comparing the bubble size distribution with velocity profile, high velocity gradient was detected at the upstream and downstream flow transition region around the recycle flow inlet. The high velocity gradient was proved to be the key factor causing bubble coalescence. At last, the influence of mainstream and recycle flow rates on bubble size was investigated. Bubble size in the contact zone increased with the increase of recycle flow rate because the velocity gradient at upstream and downstream transition region increased, which can enhance the bubble coalescence. On the contrary, mainstream flow rate showed no effect on bubble size distribution in the contact zone.

Key words：air flotation；bubble；coalescence；velocity gradient；population balance model；numerical simulation；computational fluid dynamics

中图分类号：TQ 028.4

文献标志码：A

文章编号：0438—1157（2016）06—2300—08

DOI：10.11949/j.issn.0438-1157.20151664

基金项目：中央高校基本科研业务费专项资金项目（14CX06097A）。

Corresponding author:Prof. WANG Zhenbo, wangzhb@upc.edu.cn