基于蒙特卡洛法的大型公共建筑造价风险评估
2016-07-06朱秀段黄茂林
朱秀段 黄茂林
(1.华南理工大学建筑设计研究院,广东 广州 510641; 2.广东省建筑设计研究院,广东 广州 510010)
基于蒙特卡洛法的大型公共建筑造价风险评估
朱秀段1黄茂林2
(1.华南理工大学建筑设计研究院,广东 广州510641;2.广东省建筑设计研究院,广东 广州510010)
摘要:针对大型公共建筑前期造价管理薄弱、风险性大等特点,建立了蒙特卡洛法的风险评估模型,并结合工程实例,阐述了该模型在工程造价风险评估中的应用,为投资者合理确定和有效控制项目的前期造价提供理论依据。
关键词:大型公共建筑,造价风险,蒙特卡洛法,风险评估
1概述
大型公共建筑具有大规模、大投资、工艺复杂等特点,使得项目建设过程面临很大的造价风险。从业主的角度,对项目建设前期阶段的造价风险进行评估。
1.1造价风险
造价风险就是指在项目建设过程中,存在影响造价的各种不确定性因素。
大型公共建筑从前期阶段到竣工使用,各个阶段的造价对项目的影响程度是不同的。根据研究发现,项目前期决策与初步设计阶段对项目投资的影响是最大的,这就体现了项目前期造价风险评估的必要性和重要性。
1.2造价风险评估
风险评估的方法很多,有期望值法、专家决策法和模拟仿真法等。蒙特卡洛法是随着计算普及而被广泛应用的一种评估方法,它是利用统计学和概率学理论,在已知可得的少量数据下,通过模拟实验来获得大量数据。
在项目前期,业主希望将项目造价控制在其可承受的风险范围内,蒙特卡洛法正好满足这种在前期信息少或无信息的条件下预测未来的需要。
2蒙特卡洛法模拟
2.1蒙特卡洛法的基本原理
蒙特卡洛法通过模拟事物的形成过程,来求得接近事实的数据,用数学公式表达如下:
假设目标函数Y=f(X1,X2,X3,…,Xm)。
假定随机变量X的概率分布已知,通过试验抽样N,可得到N组变量X的值(X1i,X2i,X3i,…,Xmi),然后按函数关系确定N个目标抽样值Y。这样只要N足够大,就可得到接近实际情况的Y概率分布函数。
2.2确定造价风险的概率分布
由上述基本原理可知,蒙特卡洛法必须先已知自变量X的概率分布。由于不同的风险,其概率分布形式也不同,因此须在可接受误差范围找到一种能够代替其他概率分布的近似分布。根据现有研究是选取三角分布。它需要的参数少且易得,如图1所示,且可简化很多种分布形式,如图2所示。
从图2可以看出,最大值和最小值的出现概率都很小,而出现概率较大是最可能值周围。利用三角分布来近似各种实际分布,可大大简化计算过程。
根据项目造价的组成可知,项目总造价是由各项目具体活动的子项造价组成。由于前期造价信息和资料的缺乏,每个子项可根据专家决策法来获得最小造价、最可能造价和最大造价,从而获得该子项造价的三角分布函数。然后利用反函数原理求得造价关于概率的表达式Xi(y),将全部子项造价Xi(y)汇总可得到含风险总造价的表达式SC=∑Xi(y)。然后据此利用蒙特卡洛法和计算机对总造价SC进行大量模拟试验,最后统计这些试验值,获得含风险总造价的概率分布。
2.3基于蒙特卡洛法的造价风险评估模型
2.3.1设计模型
基于蒙特卡洛法的模拟试验,其模型设计如图3所示。
2.3.2造价风险概率分布
根据上述确定的三角分布作为各子项目含风险造价的概率近似分布,其密度函数和分布函数如下:

其中,a为最小值;b为最大值;c为最可能值。

其中,a为最小值;b为最大值;c为最可能值。
由于含风险的子项造价变量x在某特定范围内也是随机的,这正好体现了其造价的风险性。令Y的值在(0,1)上随机均匀分布,Y=F(X),其反函数X=F′(Y)。由此可知,每产生一组Y值,就可得到一组服从该函数分布的X预测值。
2.3.3模拟试验误差分析
进行蒙特卡洛法模拟试验时,主要产生两种误差:一种是试验过程产生的误差;另一种是用三角分布代替实际分布产生的误差。
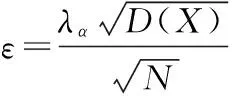
其中,α为置信水平;λα为正态差。

3实例应用分析
3.1项目概况
某拟建大型公共建筑项目经批准的概算费用组成(不含预备费)如表1所示。
3.2模型应用
首先结合类似工程资料,应用专家决策法或期望值预测出各子项造价的最大值、最小值及最可能值。此处,有个前提是假定各个子项造价之间是相互独立存在的,这样项目总造价SC就可以由各子项目造价累加得到,即:
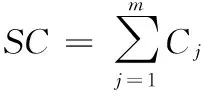
利用模型对该项目进行5 000次的模拟,得到5 000个模拟试验结果。对结果进行统计分析,得到该含风险总造价的均值、标准差和结果的波动范围如表2所示。
将波动范围(19.688 1~22.886 0)均等划分为50个区间,然后分别计算各个区间中试验结果出现的频数、累积频数、频率以及累积频率,再制成概率分布图和累积概率分布图如图4,图5所示。
3.3造价风险评估
通过前面蒙特卡洛模拟试验结果分析,可对该项目的风险评价提供如下依据。
3.3.1超概算风险评估
从上述结果可看出拟建项目含风险总造价呈现明显的正态分布。模拟结果主要出现范围为20.455 6亿元~21.606 8亿元,该区间的分布占到总试验结果的75.1%。由大数定则可得,费用预测落在该范围是相对合理的造价。结果在20.775 4亿元~20.839 3亿元区间的概率是最大的,出现频率为5.06%。

文章编号:1009-6825(2016)14-0214-03
收稿日期:2016-03-04
作者简介:朱秀段(1985- ),女,助理工程师;黄茂林(1985- ),女,助理工程师
中图分类号:TU723.3
文献标识码:A
