地下结构孕险环境危险性预警的改进SVM模型*

王凤山　戎全兵　张宏军

地下结构孕险环境危险性预警的改进SVM模型*

王凤山①②戎全兵②张宏军②

( ①解放军理工大学野战工程学院南京210007)

( ②解放军理工大学指挥信息系统学院南京210007)

摘要针对地震作用下孕险环境样本数据有限、复杂非线性等特点，提出了一种基于最小二乘支持向量机的地下结构孕险环境危险性预警方法。围绕地震后效应的地下工程区域孕险环境危险性预警目标和特征参数，设计孕险环境危险性问题的向量机表示形式，提出孕险环境危险性支持向量机训练工作机制，利用支持向量机结构风险最小化原则和非线性映射特性，建立基于最小二乘支持向量机的地下结构孕险环境危险性预警模型及其算法组件，并利用遗传算法优化其惩罚函数和核函数参数，隐式表达孕险环境危险性与其影响因素之间的非线性关系。结果表明，模型具有有效的小样本学习能力，具有较高的拟合和预测精度，明显优于神经网络等预测模型。

关键词孕险环境风险预警地下结构支持向量机遗传算法

0引言

地震作用下地下工程区域环境平衡失稳，其结构和物理力学性质方面表现为宏观和微观上的不连续性、非线性等特点(Omeretal.，2010； 杨志华等， 2013)，考虑区域孕险环境受到岩性、岩层倾向、地形、坡体形态、水条件、岩土含水量、岩体节理裂隙发育状况等等因素综合影响(孙海峰等， 2013)，有效预测与控制地下结构区域环境变形危险性，是地下结构安全监控关注的重要问题。

岩石力学与工程的智能分析方法(遗传算法、神经网络等)是国内外科技工作者广泛关注的研究课题，支持向量机(SupportVectorMachine，简记为SVM)自20世纪90年代问世以来，其在处理高维数、复杂非线性以及全局优化等方面的优良性能，受到各个研究领域的广泛关注，迅速应用于岩土力学与工程的各个方面(赵洪波， 2008)，如成都理工大学利用逐类组合支持向量机预测边坡稳定性(匡野， 2013)，Wangetal.(2010)利用最小二乘支持向量机隐式表达防护工程损毁与其影响因素之间的非线性关系； 董辉等(2012)建立工程先验知识辨识下的滑坡非平稳变形支持向量机预测模型。

孕险环境危险性判决是对塌陷、滑坡、泥石流等多样性潜在灾害的风险决策，是地下工程区域环境在地震灾害后效应作用的系统分析(黄润秋， 2011)，各类风险事件影响因子及其变量参数存在很大的相异性(李天斌， 2008)； 同时，地震作用下的地下工程区域环境存在特征参数获取困难的现实约束，如何集成专家智慧和特征参数，利用支持向量刻画孕险环境因子与危险性对象之间的非线性依赖关系，形成快捷、科学的孕险环境危险性评估工具，对有效辨识和掌握地下工程环境的发育特征和演化规律，对地下结构震害损失和科学防治具有重要价值。

1孕险环境预警问题SVM表示

地震作用下地下工程区域孕险环境危险性是典型的非线性问题，包括状态评价和风险预测两方面问题，其本质是围绕地质灾害危险性这一目标问题展开对孕险环境特征参数的多属性数值计算和模型推理(Lietal.，2012)。

归纳起来(赵洪波， 2008；Omeretal.，2010； 孙海峰等， 2013)，地震载荷作用后的地下工程孕险环境主要与地形地貌高差变异系数(C1)、地质环境坡度变异系数(C2)、土地塌陷裂缝规模(C3)、水资源变化强度(C4)、岩体结构完整性系数(C5)、地质结构面强度系数(C6)、坡体黏聚力(C7)、岩体变形模量(C8)、表面变形速率等特征参数相关。

地下结构孕险环境预警支持向量机，把工程环境破坏与变形及其危险性看作是客观条件变化的序列，将问题转化为“如何利用样本挖掘出危险性规律，进而预测检验样本的危险性指数？”。

令C={Cj|1≤j≤n}表示孕险环境危险性的机理因素或特征参数集合，利用支持向量机方法描述孕险环境危险性与影响因素的映射关系，即：

(1)

2孕险环境危险性SVM训练工作机制

SVM具备严格的理论和数学基础，其核心思想就是学习机器要与有限的训练样本相适应，是继神经网络之后机器学习领域的研究热点(袁辉等， 2014)。

围绕地震作用下地下结构孕险环境危险性预警任务和功能约束，遵循支持向量机的基本原理和组合预测模式(耿睿等， 2008)，设计孕险环境危险性向量机训练模式(图1)，即其训练和检验的推理工作机制。

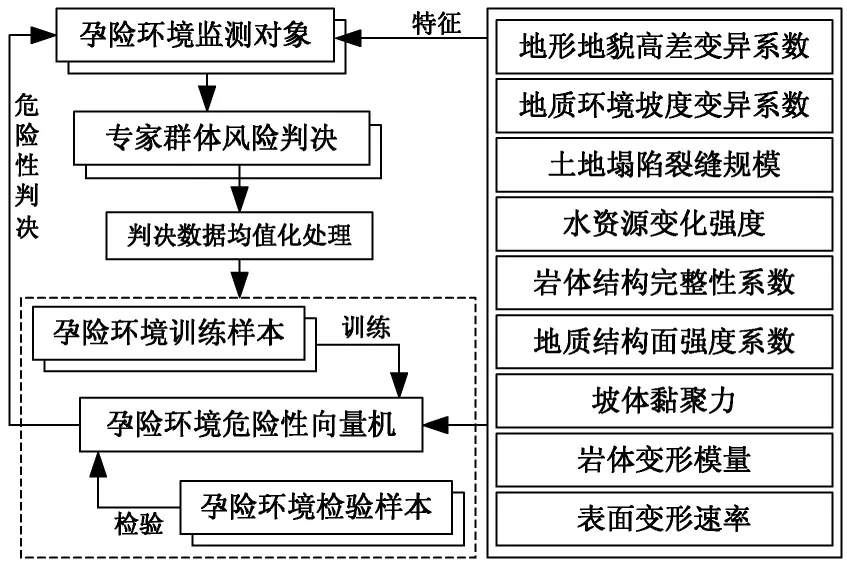
图1　孕险环境SVM训练模式Fig. 1　SVM Training mode on the risk pregnant environment

样本是孕险环境危险性SVM学习训练的前提条件。鉴于震后工程区域地质等的特殊场景约束，以现场监测、遥感解译、专家全体决策为基础，提供特征参数的赋值和样本集合，称之为数据发生器。其中，孕险环境监测单元样本的风险指数为0-10，即yi∈[0， 10]表征风险指数的变化范围。

孕险环境危险性SVM包括训练和检验两个步骤，通过检验控制向量机的预测误差，进而调整向量机参数，重新学习训练，直到向量机误差满足模型推理的精度约束。

3孕险环境危险性SVM预警模型

3.1基于SVM的地下结构孕险环境预警原理

Vapnik教授等提出的支持向量机，是基于统计学习理论的小样本训练、学习方法，其核心思想是遵循结构风险最小化原则，基于内积函数定义的非线性变换方法，实现非线性多元输入空间到高维空间的映射变换，寻找输入和输出之间的隐式关系和函数表达(Bertalanffyetal.，1973)。

(2)

根据结构风险最小化原则(Bertalanffyetal.，1973)，式(2)的危险性回归预测问题就是寻求使下面风险最小化函数，如式(3)：

(3)

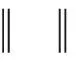
(4)

3.2基于LS-SVM的孕险环境危险性预警模型

(5)

利用Lagrange法求解模型(5)的优化问题，定义Lagarangian函数：

(6)

其中，αi是Lagrange乘子，也称为支持值。

根据优化条件和相应的对偶形式，通过L(，b，ћ，α)求、b、ћ、α的偏导，将LS-SVM模型(6)转化为求解线性方程，如(7)。

(7)

计算模型(7)，可得到：

(8)

(9)

(10)

至此，可得最小二乘支持向量机的地震作用下地下结构孕险环境危险性估计函数，即预警模型：

(11)

3.3孕险环境危险性预警支持向量机参数优化

根据有限样本信息，寻求模型复杂性和学习能力之间最佳折衷，有效实现小样本空间的高维非线性系统精确拟合，是SVM的本质特征和推广应用价值(Renetal.，2010)。

惩罚参数γ、不敏感损失参数ε、核参数δ，对LS-SVM回归模型的预测效果具有较大影响，为获取具有较高预测预警性能的SVM回归模型，需要对γ、δ、ε进行组合优化，从而获取较高预测性能的地下结构孕险环境危险性SVM回归模型。利用遗传算法(GeneticAlgorithm，简称为GA)建立最小二乘支持向量机的参数选择模型，进行参数的优化(甘秋明， 2012)，其流程如图2 所示。

图2　GA优化最小二乘支持向量机参数流程Fig. 2　GA optimized parameter workflow on Least Squares Support Vector Machine

遗传算法优化最小二乘支持向量机(简记为GA-LS-SVM)的具体建模步骤(Yang， 2011)，如下：

(1)LS-SVM参数编码与GA参数设置：将LS-SVM训练参数γ、δ、ε以二进制形式进行染色体基因编码，编码范围分别设定为[1， 100]、[0， 2]、[0.000O1， 0.01]；GA参数设置，如交叉率0.78、变异率0.05，随机产生表示LS-SVM参数值的染色体，种群数为30。

(2)种群适应度评估：采用平均相对误差作为适应度函数来衡量选取参数γ、δ、ε的优劣。

(3)染色体选择机制：根据种群个体适应度，通过轮盘赌法，复制具有较高适应度值的染色体。

(4)染色体交叉机制：采用单点交叉法，以交叉率交换染色体串结构中特征数据获得到新一代染色体。

(5)染色体变异机制：随机选择种群个体，根据随机概率改变染色体结构数据中某个基因的值，产生一组新的染色体。

(6)当满足终止条件时，遗传算法优化地下结构孕险环境危险性LS-SVM模型参数的进化迭代过程结束，否则转到步骤②。

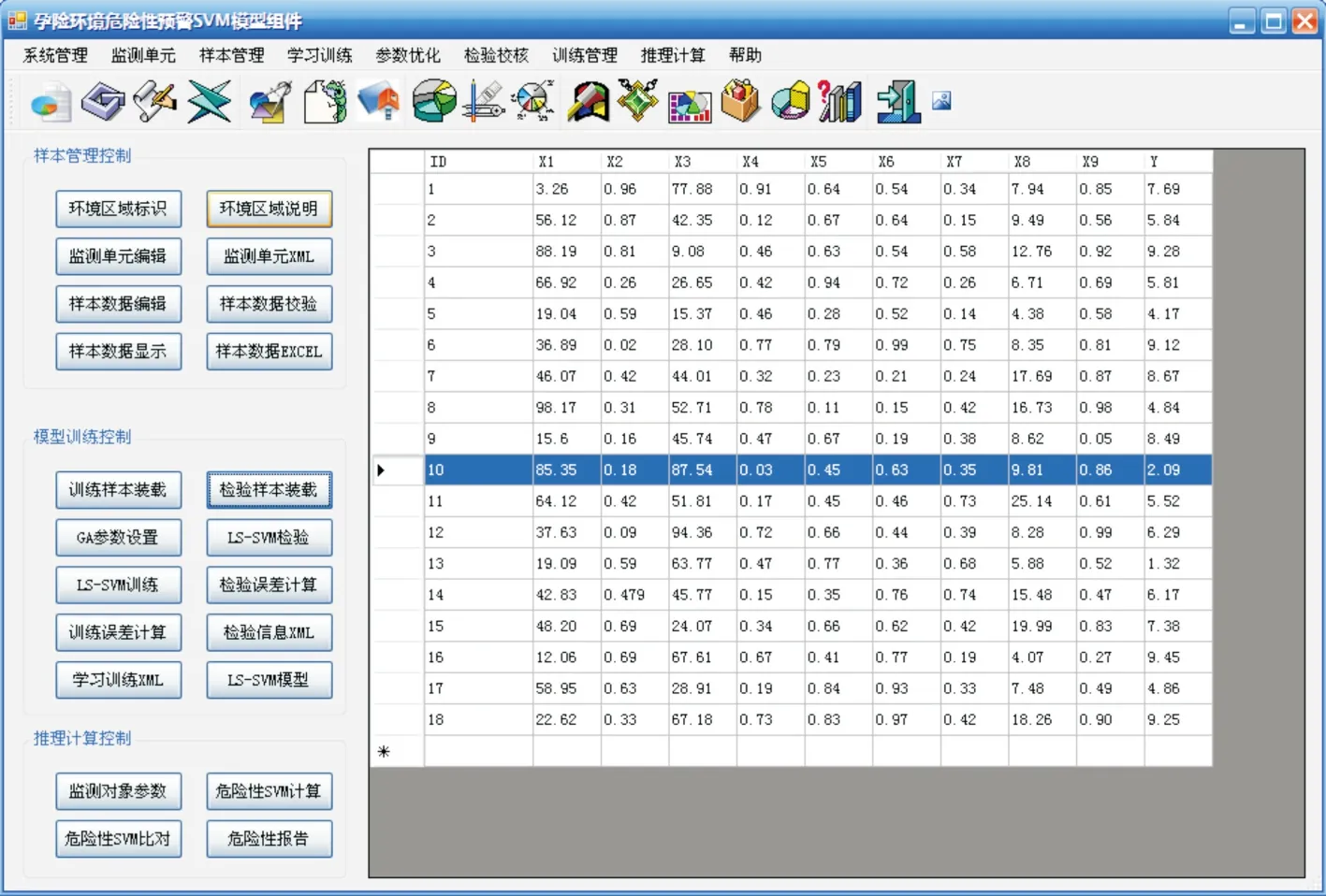
图3　孕险环境预警SVM模型组件界面Fig. 3　Early-warning SVM component model interface on the risk pregnant environment

3.4孕险环境危险性预警支持向量机

遵循结构上反映最小二乘支持向量机模型算法本质思想和关键概念的前提条件，以通用仿真引擎为运行环境，在VisualC# 和.NET语言环境下，集成MATLAB数学模型控件(Takahashietal.，2006)，研制孕险环境危险性预警SVM模型组件(COM组件)如图3 所示，即组件式地下结构震害孕险环境危险性预警支持向量机模型。

模型直接服务于地下结构震害风险分析系统软件平台，包含孕险环境监测单元、样本管理、学习训练、参数优化、检验校核、推理计算等功能模块。设计孕险环境危险性预警模型实验的训练样本和检验样本如表1、表2所示。

表1　地下结构孕险环境危险性训练样本

机器学习预测的第一步骤就是根据给定训练样本对地下结构孕险环境危险性问题的输入输出关系进行估计。通过GA-LS-SVM算法的模型组件的学习训练，其输出结果表明(表1)，在允许的误差约束范围内，GA-LS-SVM模型具有孕险环境危险性预测的初步可行性。

表2　地下结构孕险环境危险性检验样本

利用估计的规律性对孕险环境危险性检验样本进行预测，是机器学习的第二步骤，即预测模型的适用性问题，不能仅根据训练数据的拟合近似程度来判断，而是应根据它的推广能力和准确率来判断。

为验证预警模型的可靠性，同时选取BP神经网络算法及SVM算法、LS-SVM算法，检验训练样本产生的模型，确定5组“地下结构孕险环境危险性”预测值，并与评估值作比较，检验模型的学习推广能力(表3)。

表3　地下结构孕险环境危险性检验误差

表3误差比较，体现了危险性预警模型需要满足结构风险最小化原理约束要求。BP神经网络是训练样本记录趋于无穷大时的渐近理论，即训练样本记录趋于无穷大时，训练误差才收敛于实际风险； 而地下结构孕险环境危险性预警注定是一个训练样本数据有限的状况，故只能选用有限样本情况下的机器学习理论。

BP算法用于地下结构孕险环境危险性预警的可行性明显弱于SVM、LS-SVM算法，SVM和LS-SVM算法均可以很好的表达地下结构孕险环境危险性预测影响因素之间的非线性映射关系，模型具有很好的推广预测能力。

同时，利用遗传算法优化最小二乘支持向量机的训练参数，明显提高了最小二乘支持向量机的预警精度，平均误差为2.11%，远低于常规支持向量机和最小二乘支持向量机的7.31%和7.74%的数值误差。

4结论

有限训练样本条件下，地下结构孕险环境危险性预警支持向量机，分析了危险性与其影响因素之间的非线性关系，结果表明GA-LS-SVM对孕险环境结构破坏与变形预测具有较高的精度。

(1)地震作用下的地下工程孕险环境危险性受很多因素影响，并且之间的关系是高维、非线性、复杂的关系，用传统的建模方法很难处理，LS-SVM方法很好地处理了这种关系，不仅保证了经验风险的最小化，而且使期望风险也降低到最低程度，使判别结果更趋于合理。

(2)遗传算法改进、优化LS-SVM建立孕险环境危险性预警模型，根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折衷，克服了神经网络学习方法中网络结构难以确定、收敛速度慢、训练时需要大量样本等缺点，避免了因统计数据不足使得统计结果不准的普遍问题，解决了孕险环境预警问题的数据缺乏“瓶颈”问题。

(3)LS-SVM通过学习训练获得孕险环境危险性的隐式表达，整个过程非常清晰、直观，并具有很好的推广能力和很高的准确率，可见LS-SVM在该领域有着很强的优势和广泛的应用前景； 但学习训练的准确性和可靠性很大程度上取决于选用样本的典型性和代表性，取决于核函数的选择，故要予以重点关注； 同时，模型组件还可以进一步功能优化，结合其他应用领域实际，对相关问题的的量测、评估、设计提供模型支持和便利工具。

参考文献

BertalanffyLV. 1973.GeneralSystemstheory[M].NewYork：GeorgeBrazillerInc．

DongH，ChenJB，YangGY，etal. 2012.SVMpredictionofnonstationarydeformationoflandslidebasedonidentificationwithpriorknowledge[J].RockandSoilMechanics，33(8)： 2366～2372，2382．

GanQM. 2012.Passengertrafficvolumeforecastingbasedonsupportvectormachineoptimizedbygeneticalgorithm[J].HighwayEngineering，37(6)： 192～195．

GengR，CuiDH，XuB. 2008.Supportvectormachine-basedcombinationalmodelforairtrafficforecasts[J].JournalofTsinghuaUniversity(Science&Technology)， 48(7)：1205～1208．

HuangRQ. 2011.AftereffectofgeohazardsinducedbytheWenchuanearthquake[J].JournalofEngineeringGeology，19(2)： 145～151．

KuangY. 2013.Studyonpredictionofslopestabilitybasedontermwise-combinationsupportvectormachine[J].SubgradeEngineering，20(5)： 73～77．

LiSJ，ZhaoHB，RuZL. 2012.DeformationpredictionoftunnelsurroundingrockmassusingCPSO-SVMmodel[J].JournalofCentralSouthUniversity，19(11)： 3311～3319．

LiTB. 2008.FailurecharacteristicsandinfluencefactoranalysisofmountaintunnelsatepicenterzonesofgrearWenchuanEarthquake[J].JournalofEngineeringGeology，16(6)： 742～750．

LingA，YeS. 2013.ModelpredictivecontrolfornonlineardistributedparametersystemsbasedonLS-SVM[J].AsianJournalofControl，15(5)： 1407～1416．

OmerA，YoshimiO，MelihG，etal. 2010.Responseandstabilityofundergroundstructuresinrockmassduringearthquakes[J].RockMechanicsandRockEngineering，43(6)： 857～875．

RenY，BaiGC. 2010.DeterminationofoptimalSVMparametersbyusingGA/PSO[J].JournalofComputers，5(8)： 1160～1168．

SunHF，JingLP，WangSW，etal. 2013.Experimentalstudyofseismicfailuremechanismofundergroundstructure[J].ChineseJournalofRockMechanicsandEngineering，32(S2)： 3267～3275．

SuykensJAK，VandewalleJ. 1999.LeastSquaressupportvectormachineclassifiers[J].NeuralProcessingLetters，9(3)： 293～300．

TakahashiY，FenvesGL. 2006.Softwareframeworkfordistributedexperimental-computationalsimulationofstructuralsystems[J].EarthquakeEngineeringandStructuralDynamics，35(3)： 267～291．

WangFS，ZhangHJ，ZhuWH. 2010.Studyofdamagepredictingmodelonsubsurfaceengineeringstructure[C]∥2010InternationalConferenceonComputing，ControlandIndustrialEngineering(CCIE2010).IEEEHongkongSection： 329～332．

YangJY. 2011.AnovelintelligentconditionevaluationmethodofmechatronicequipmentbasedonSVMandGA[J].InternationalJournalofAdvancementsinComputingTechnology，3(7)： 229～236．

YangZH，LanHX，ZhangYS，etal. 2013.Rockdynamicresponseofrailwaytunneltraversingthroughfaultunderstrongearthquake[J].JournalofEngineeringGeology，21(2)： 171～181．

YuanH，WangFS，XuJH，etal. 2014.TrainingsamplereductionmodelofdamagesimulationofprotectiveengineeringbasedonimprovedSVM[J].JournalofPLAUniversityofScienceandTechnology(NaturalScienceEdition)，15(2)： 152～157．

ZhaoHB. 2008.Analysisofsupportvectormachineinrockmechanicsandengineering[M].Beijing：ChinaCoalIndustryPress．

董辉，陈家博，杨果岳，等. 2012. 工程先验知识辨识下的滑坡非平稳变形支持向量机预测[J]. 岩土力学，33(8)： 2366～2372,2382．

甘秋明. 2012. 基于遗传算法优化支持向量机的公路客运量预测[J]. 公路工程，37(6)： 192～195．

耿睿，崔德光，徐冰. 2008. 应用支持向量机的空中交通流量组合预测模型[J]. 清华大学学报(自然科学版)， 48(7)：1205～1208．

黄润秋. 2011. 汶川地震地质灾害后效应分析[J]. 工程地质学报，19(2)： 145～151．

匡野. 2013. 基于逐类组合支持向量机的边坡稳定性预测研究[J]. 路基工程，20(5)： 73～77．

李天斌. 2008. 汶川特大地震中山岭隧道变形破坏特征及影响因素分析[J]. 工程地质学报，16(6)： 742～750．

孙海峰，景立平，王树伟，等. 2013. 地下结构地震破坏机制试验研究[J]. 岩石力学与工程学报，32(S2)： 3267～3275．

杨志华，兰恒星，张永双，等. 2013. 强震作用下穿越断层隧道围岩力学响应研究[J]. 工程地质学报，21(2)： 171～181．

袁辉，王凤山，许继恒，等. 2014. 基于改进SVM的坑道毁伤仿真训练样本约简模型[J]. 解放军理工大学学报(自然科学版)，15(2)： 152～157．

赵洪波. 2008. 岩土力学与工程中的支持向量机分析[M]. 北京：煤炭工业出版社．

RISKPREGNANTENVIRONMENTEARLY-WARNINGMODELFORUNDERGROUNDSTRUCTUREBASEDONIMPROVEDSUPPORTVECTORMACHINE

WANGFengshan①②RONGQuanbing②ZHANGHongjun②

( ①College of Field Engineering，PLA University of Science &Technology，Nanjing 210007)

( ②College of Command Information Systems，PLA University of Science &Technology，Nanjing 210007)

AbstractThis paper addresses the limited complex and nonlinear characteristics in earthquake-induced risk pregnant environmental sample data. It puts forward a risk early-warning method for such pregnant environment around underground structure on least squares support vector machine. Around risk early-warning object and parameters in after-earthquake risk pregnant to underground engineering, the risk pregnant environment is expressed and designed with Support Vector Machine, and SVM training mechanism was proposed for risk pregnant environment. Such risk early-warning mold and the component is erected for risk pregnant environment around underground structure on least squares support vector machine, which utilizes structural risk minimization principle and nonlinear mapping feature of SVM, and optimizes the penalty function and kernel function parameters with Genetic Algorithm. The model implicitly expresses the non-linear relationship among the risk pregnant environment and factors. Case study shows such model has an effective small sample learning ability, well fitting and forecasting accuracy, which excels the predicting model with BP nerve network．

Key wordsRisk pregnant environment, Risk early-warning, Underground structure, Support Vector Machine, Genetic Algorithm

DOI:10.13544/j.cnki.jeg.2016.02.020

* 收稿日期：2015-04-11; 收到修改稿日期： 2015-08-29.

基金项目：国家自然科学基金(51308541)，江苏省自然科学基金(BK20130066)资助.

第一作者简介：王凤山(1978-)，男，博士，副教授，主要从事防护工程系统毁伤建模与仿真分析方面研究工作. Email: WFS919@126.com

中图分类号：P642.22

文献标识码：A