关于一种开尔文方程推导方法的讨论

刘　健　肖赛君　章　俊　张月云　田余余

(安徽工业大学冶金工程学院，安徽马鞍山243002)



关于一种开尔文方程推导方法的讨论

刘健肖赛君*章俊张月云田余余

(安徽工业大学冶金工程学院，安徽马鞍山243002)

摘要：不同版次物理化学教材对开尔文方程推导的方法不同。本文通过对吉布斯界面热力学基本方程中球状液滴压强的分析，并依据对于弯曲液滴，附加压力本质上就是由弯曲液面表面张力引起的，得出某物理化学教材中，对小液滴的气液两相平衡过程，其吉布斯自由能的变化为零。对于恒温下，把处于外压为p0的平面液滴分割为处于外压为pr的小液滴的过程，其吉布斯自由能的变化为2σM/ρr。

关键词：开尔文方程；弯曲液滴；弯曲液滴压强

www.dxhx.pku.edu.cn

开尔文方程是界面现象中一个重要公式。某《物理化学》教材采用基于始终态相同时不同途径其状态函数的改变量相同的方法进行推导[1,2]。李爱昌[3]发现该教材第5版2008年之后的印刷本(版次相同)与之前的开尔文方程推导过程不同。经过对比分析，李爱昌认为2008年之后的印刷本推算方法正确，而之前的计算过程是错误的。

本文依据吉布斯界面热力学基本方程的建立过程，得出了界面热力学基本方程中小液滴压强的正确含义，并以此为基础得出了与文献[3]相反的结论。本文认为，该《物理化学》教材中，对小液滴的气液两相平衡过程，其吉布斯自由能的变化为零。对于恒温下，把处于外压为p0的平面液滴分割为处于外压为pr的小液滴的过程，其吉布斯自由能的变化为2σM/ρr。

1　开尔文方程推导简介

李爱昌[3]曾对开尔文方程的推导方法进行总结，认为其推导方法大致可以分为两类：第一类是基于气液平衡时化学势相等的方法；第二类是基于始终态相同时不同途径其状态函数的改变量相同的方法。

王竹溪先生[4]所著《热力学简程》是国内教材中最早采用第一类推导方法推导开尔文方程的。该方法的推导主要依据恒温下化学势随压力的变化微分式dμ= Vmdp计算，然后采用拉普拉斯公式计算附加压力即可得出开尔文方程的表达式。以文献[5]、[6]为例进行说明。

依据dμ= Vmdp以及拉普拉斯公式，将1 mol大块平面液体变成半径为r的小液滴，前后化学势之差见式(1)。

式(1)中p0为与平面液体平衡的气相压强，Vm为纯液体的摩尔体积。依据液体与其平衡气相化学势相等，可以推导出平面液体化学势和小液滴化学势的表达式，分别见式(2)和式(3)。

式(3)中的pr为与小液滴平衡的气相压强。由式(2)与式(3)可得式(4)。

将式(4)代入式(1)得式(5)，即开尔文方程，式(5)中M、ρ分别为液体的摩尔质量和密度。

本文所讨论的《物理化学》教材采用的是第二类推导方法，即基于始终态相同时不同途径其状态函数的改变量相同的推导方法，详细推导方法见第2节。

2　一种开尔文方程推导方法简介

某《物理化学》教材在讲述开尔文方程推导时，采用的方法是基于始终态相同时不同途径其状态函数的改变量相同的方法进行推导。该推导方法依据图1所示物理过程展开推导[1,2]。

图1　基于始终态相同的不同热力学途径构造[2]

所有过程均在恒温下发生。过程①是平面液体的气液两相平衡；过程③是小液滴的气液两相平衡；过程②是恒温下，把处于外压为p0的平面液滴分割为处于外压为pr的小液滴的过程；过程④是恒温条件下，蒸气的恒温变压过程。

依据李爱昌[3]的总结，该《物理化学》教材在2007年以前的印刷本关于图1中各步骤吉布斯自由能的变化值计算如下，本文称为计算方法1。

而2008年以后的印刷本(版次相同)计算如下，本文称为计算方法2。

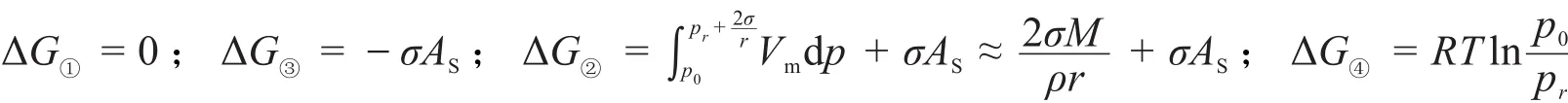
对于图1所示物理过程，还有一种计算方法[7]。为了进行对比分析，本文也将其列出，称该方法为计算方法3。不过对于图1所示物理过程，计算方法3考查的是dn mol的物质进行迁移的过程。

对比计算方法1与计算方法2可知，两种方法的根本区别在于对过程②和过程③的吉布斯自由能计算上。

对于过程②的吉布斯自由能计算，李爱昌[3]依据文献[8]提供的表面热力学基本方程来论证计算方法2中ΔG②计算的合理性。文献[8]提供的界面热力学认为，对于有弯曲界面的气液两相系统，恒温下，把dn mol纯液体自水平液面转移至小液滴上，则系统吉布斯自由能的变化为：

式中α表示体相。对式(6)进行积分，即得式(7)。

由此证明了计算方法2中过程②的吉布斯自由能计算正确。

对于第二点，李爱昌[3]依据文献[9]提供的弯曲界面相平衡判据，见式(8)。

式(8)中，α也表示体相。当小液滴变成与之平衡的气体时，由于化学势相等，体相与气相的μn抵消，而多出一项表面能－σAS。所以计算方法2中过程③的吉布斯自由能计算正确。

3　对该类开尔文推导方法的分析讨论

本节分别对图1所示过程②和过程③吉布斯自由能计算方法进行讨论分析。

3.1关于过程②吉布斯自由能的计算讨论

对ΔG②的计算，关键是式(1)中pα的具体值。对于平面液滴，pα是外界气体压强。对于球状液滴，pα有两种数值。一种是外界气体压强加上附加压力，一种也是外界压强。对于球状液滴，如果其压强也是外界气体压强，则式(6)变成式(9)。

式(9)就是计算方法3对过程②的计算结果。

既然李爱昌[3]依据文献[8]提供的界面热力学基本方程进行分析，要想确定球状液滴的压强，就应从界面热力学基本方程的建立过程进行考虑。

构造图2所示物理模型。界面热力学的建立方法有古根海姆法和吉布斯法，在表面化学的教材中一般称为界面相法和相界面法[8]。李爱昌[3]依据文献[8]提供的表面热力学基本方程是采用吉布斯法建立的。而吉布斯法认为界面相是没有体积的几何相，所以，在图2中(α)表示整个液相，而不单指体相。

在恒温恒外压下，小液滴体积增大dV时，依据热力学第一定律和第二定律，有：

从式(10)看，即从热力学基本方程的推导来看，无论是平面液滴还是球状液滴，液体压强都是外界气体压强，因为体积功的计算公式就是外界压强与体积变化值的乘积。

另外，将式(10)看成U = f(S, V, As)三元函数的全微分，则小液滴压强在热力学基本方程中定义见式(11)。

图2　恒温恒外压下的球状液滴

式(11)表明，式(10)中小液滴的压强是指在熵和液滴表面积均不变时，单位体积变化对应的内能变化。值得注意的是，对于小液滴，体积与表面积不是独立变量，体积的变化会引发表面积的变化。但是，一旦写成全微分形式，必须将体积与表面积看成独立变量处理。可将球状小液滴假想成玻璃杯中的平面液滴，此时平面液体体积的变化不影响气液表面积的变化，该状态对应的式(11)的计算值也是指外界气体压强。

以上分析表明，计算方法2对ΔG②的计算是错误的，而计算方法3对ΔG②的计算是正确的。

在计算方法1对ΔG②的计算中，对小液滴压强的处理与计算方法2相同，那么该计算过程也是错误的吗？实际上计算方法1对ΔG②的计算方法依据的热力学基本方程为式(12)，与李爱昌[3]依据文献[8]提供的表面热力学基本方程式(10)不同。

如式(12)所示，对于弯曲液滴热力学基本方程，式(12)中没有σdS项。即式(12)的处理方法是将吉布斯自由能看成二元函数，即G = f(T, p)，而不是像式(6)对应的三元函数G = f(T, p,AS)。采用式(12)计算图1所示过程②，它的含义是平面液体变成球状液滴时，认为表面能转变为对体相α的附加压力，所以计算方法1与计算方法3对ΔG②的计算是等价的，如式(13)所示。

另外，从拉普拉斯方程的力学推导方法可以看出，附加压力是界面相对体相的作用力。对整个小液滴而言，该力属于内力。采用吉布斯界面热力学基本方程时，界面相为没有体积的几何相。从这个角度看，式(6)中的p(α)是整个小液滴的压强，在数值上等于外界气体压强。好比一个人称体重时，用手使劲向下给头施加压力。不管他施加多大的力，他对称的压力是不会改变的。也就是，对于整个小液滴而言，达到力学平衡时，其压强应该等于外界大气压，而不管表面相对体相的附加压力。

还值得说明的是，李爱昌[3]依据文献[8]提供的表面热力学基本方程来计算ΔG②。而文献8在开尔文方程的推导过程中，对平面液滴变成小液滴的ΔG②的计算与计算方法1相同。

综上所述，对ΔG②的计算，计算方法2是错误的，而计算方法1和3是正确的。

3.2关于过程③吉布斯自由能的计算讨论

图1所示过程③描述的是恒温恒外压条件下，球状液滴与气体的相平衡过程，其物理模型见图2。依据热力学第二定律，在恒温恒外压条件下，当小液滴中有dn mol的物质转移到气相中时，dG=dG(α)+dG(β)=0，这也就是说明恒温恒压下，当n mol小液滴全部变成与之平衡的气体时，整个过程ΔG=0，即ΔG③= 0；如果ΔG③≠0，则说明该过程没有达到气液两相平衡。

对于ΔG③，李爱昌[3]依据文献[9]提供的弯曲界面相平衡判据式(8)来说明当小液滴变成与之平衡的气体时，由于两个体相化学势相等，体相与气相的μn抵消，而多出一项表面能-σAS。这种分析是错误的，同3.1节的论述，如果考虑附加压力的存在，则表明已经考虑表面能，即式(8)已经包括表面能这一项了。

综上所述，对ΔG③的计算，计算方法2是错误的，计算方法1和3是正确的。

4　结论

1)对于液体，无论是平面液体还是弯曲液滴，基于吉布斯法建立的界面热力学基本方程中的液体压强均为外界气体压强。

2)界面相对体相的附加压力来自于界面相的界面张力。当考虑附加压力来计算弯曲液滴吉布斯自由能时，等价于考虑了弯曲液面的表面能。

3)某不同版本《物理化学》教材中，对小液滴的气液两相平衡过程，其吉布斯自由能的变化为零。对于恒温下，把处于外压为p0的平面液滴分割为处于外压为pr的小液滴的过程，其吉布斯自由能的变化为2σM/ρr。

参考文献

[1]傅献彩,沈文霞,姚天扬,侯文华.物理化学(下册).第5版.北京:高等教育出版社, 2006.

[2]傅献彩,沈文霞,姚天扬,侯文华.物理化学(下册).第5版.北京:高等教育出版社, 2012.

[3]李爱昌.大学化学, 2013, 28 (2), 81.

[4]王竹溪.热力学简程.北京:人民教育出版社, 1964.

[5]范康年.物理化学.北京:高等教育出版社, 2005.

[6]胡英.物理化学.第5版.北京:高等教育出版社, 2007.

[7]李松林,周亚平,刘俊吉.物理化学(下册).第5版.北京:高等教育出版社, 2009.

[8]顾惕人.表面化学.北京:科学出版社, 1994.

[9]王竹溪.热力学简程.北京:人民教育出版社, 1964.

∙师生笔谈∙

Discussion on Derivation of Kelvin Equation

LIU JianXIAO Sai-Jun*ZHANG JunZHANG Yue-YunTIAN Yu-Yu
(School of Metallurgy Engineering, Anhui University of Technology, Ma′anshan 243002, Anhui Province, P. R. China)

Abstract:In different editions of Physical Chemistry, the Kelvin equation is derived with different methods. This paper analyses the pressure of curved liquid drop in the Gibbs interface thermodynamics basic equations, and gives a discussion on the derivation of the Kelvin equation.

Key Words:Kelvin equation; Curved liquid drop; Pressure of curved liquid drop

中图分类号：O647.1；G64

doi:10.3866/PKU.DXHX20160368

*通讯作者，Email: jxddroc@126.com

基金资助：国家自然科学基金(51404001)；国家级大学生创新创业训练(201210360002)