水下航行器艉轴球面机械密封热-结构耦合分析

周旭辉，刘正林

(武汉理工大学 能源与动力工程学院，武汉 430063)

水下航行器艉轴球面机械密封热-结构耦合分析

周旭辉，刘正林

(武汉理工大学 能源与动力工程学院，武汉 430063)

摘要：针对船舶轴系校中不良、轴承磨损等因素会导致艉轴平面机械密封面出现垂向偏移，严重影响密封面的接触压力、温度和变形等密封性能的问题，应用有限元方法建立水下航行器艉轴球面机械密封热-结构耦合模型，在不同的潜深和轴转速条件下，分析轴线垂向偏移对球面机械密封的接触压力、温度和变形状况的影响规律，结果表明，在轴线有垂向偏移的情况下，密封球面的接触压力、温度和变形与无偏移相比变化很小，说明球面机械密封具有良好的自位能力，能在不同工况条件下保持较稳定的密封性能。

关键词：球面机械密封；热-结构耦合模型；接触压力；温度；变形

艉轴机械密封是水下航行器的重要装置，对航行器的安全性、可靠性，以及生存能力具有重要的影响。当前，船用艉轴密封均采用普通平面机械密封，其动环多采用硬质合金材料，静环多采用碳石墨等非金属材料，两者组成的摩擦副具有较好的密封性能，在化工、船舶等领域得到了较广泛的应用。与化工领域不同，船用艉轴机械密封的使用环境和工况有其特殊性。受螺旋桨自重作用、轴系校中不良、轴承磨损、轴段弯曲、航行环境以及振动等因素的影响，易导致艉轴机械密封的静、动环的密封面不同轴，出现开口、偏磨等现象，引起密封面局部温度上升，泄漏量增加[1-2]。如某船轴系(轴径660 mm，转速≤500 r/min)相对轴线下降量(落差)12.7 mm，角偏差2°，与实际旋转中心偏摆3.17 mm，这种状况就会影响机械密封的密封性能及其使用的安全性与可靠性[3]。随着船舶的大型化、现代化，主机功率增大，轴系轴颈加粗，潜深增加，使得艉轴密封的工作条件也越苛刻，技术难度也越大，要求密封装置结构更加简单、可靠，静、动环具有自动对中的能力和良好的追随性。

近年来，国内外学者在机械密封结构方面开展了许多研究，如橡胶压延机、辊压机等设备就采用了楔形等静态密封来调节辊筒的偏斜，以提高汽、水的密封性能[4]。但船舶轴系艉轴的机械密封是动密封，其密封面形状没有新的改进，依旧采用平面结构[5-8]。这种平面结构会因轴线弯曲等因素引起密封性能下降，因此须进行船舶艉轴机械密封的密封面形状变革研究[9]。船舶艉轴机械密封大都是接触式密封，处于混合摩擦和边界摩擦状态[10]。密封面采用球面结构能实现摇摆、倾斜和旋转运动，具有自动调心功能[11]，可改进密封面的接触状态，提高静环的追随性，适应艉轴弯曲、轴系对中不良所造成的密封面接触不佳状况，因此应首先在理论上分析研究采用球面密封取代平面密封的可行性，开展基于艉轴轴线偏移的球面机械密封性能探讨，为密封的结构优化设计提供理论支持。

现以水下航行器艉轴球面机械密封为研究对象，聚焦艉轴轴线垂向不偏移与偏移，即对中与不对中两种状况，应用有限元方法建立不同潜深和工作转速工况下的球面机械密封的热-结构耦合模型，探讨艉轴轴线偏移、潜深变化等对密封球面的接触压力、温度、变形的影响规律。

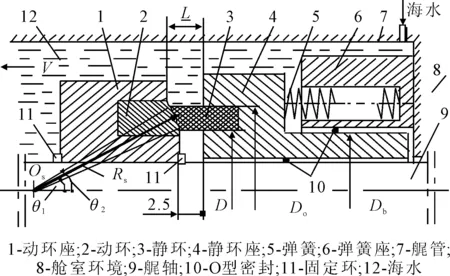
图1　艉轴球面机械密封结构示意

1球面机械密封

球面机械密封(见图1)的特点就是变革普通平面机械密封的密封面结构，采用球面代替平面实现密封功能，即艉轴机械密封的两接触表面由平面变为具有一定曲率半径的球面，从而提高机械密封对艉轴轴线偏移的自适应能力及密封性能。球面机械密封与平面机械密封一样，将动环镶嵌在动环座中，动环座通过键槽和卡环固定在艉轴上并随之旋转；静环镶嵌在静环座中，只能随静环座作轴向移动。静环座周向均布有若干根弹簧，在弹簧和密封介质的压力共同作用下，能在一定范围内补偿球面机械密封环的位移和变形，保证静、动环端面始终接触。密封环外侧为被密封介质(海水)，密封环内侧为舱室空气。

球面机械密封的结构参数见表1，各组件物性参数见表2。

表1　球面机械密封结构参数　mm

表2　球面机械密封材料参数表

2三维热-结构耦合模型

2.1建模

应用ANSYS有限元软件建立艉轴-球面机械密封热-结构三维耦合模型，见图2。

1-艉轴；2-动环座及动环；3-静环座及静环；4-弹簧图2　艉轴-球面机械密封耦合有限元模型

艉轴与球面机械密封动环座配合的轴段采用三维实体模型，其余轴段采用二维梁模型。动、静环选用SOLID 5单元，动、静环座选用SOLID 45单元，艉轴选用BEAM188单元。静环座上均布的8个弹簧选用COMBIN14单元。按表2中各组件的材料属性进行定义，并对模型划分网格，共有33 978个单元，37 650个节点,见图2 b)。

在有限元模型中，定义面-面接触对。以静环球面为接触面，动环球面为目标面。设置法向刚度系数为0.1，摩擦系数为0.03。球面间设置导热系数为108W/(m·K)，模拟热量优先由密封球面向动、静环传递。将艉轴实体的首尾端面节点分别与艉轴梁的对应节点建立MPC联系，使实体单元与梁单元的自由度相同，以保证两者单元间的力传递。

弹簧的刚度系数k由弹簧比压、静环球面面积和弹簧单元长度推导得到，k=1.4×104N/m。

2.2边界条件

2.2.1轴线偏移的施加

为了计算方便，在模拟艉轴轴线偏移时，假定艉轴段的后端面中心与密封球面的球心重合，令艉轴段长度为l，相当于球面的半径Rs，将集中力施加在球心上，使其产生最大挠度。该挠度为球心的垂向偏移值y，即作为艉轴轴线的偏移量：

(1)

式中：l——艉轴段长度，mm；

E——艉轴材料的弹性模量，MPa；

I——艉轴截面的极惯性矩，mm4。

当艉轴轴线垂向偏移量(0、1、2 mm)确定后，施加在球心处的相应集中力F就可通过式(1)求得，分别为0,3.51×105和7.02×105N。

2.2.2外部载荷施加

球面机械密封耦合模型的弹簧比压psp为0.21 MPa，海水压力p为1，2，3，4，5 MPa，相应的潜深分别为100，200，300，400，500 m。

2.2.3约束边界

1) 约束弹簧固定端的X、Y、Z方向的平动位移和绕OX，OY，OZ三轴的转动位移；约束艉轴段首端的X，Y，Z方向的平动位移。

2) 在轴线对中(无垂向偏移)情况下，对艉轴段后端施加全约束，以保证轴线不发生偏移。

2.2.4热力学边界条件

1) 密封球面热流密度计算。在实际运转过程中，球面机械密封的接触压力状况直接影响其热流密度分布，热流密度计算公式为

(2)

式中：q(r)——半径r处产生的热流密度，W/m2；

r——密封面半径(接触点到艉轴轴线的垂直距离，r=Rssinθ)，m；

f——密封球面摩擦系数，f=0.03；

pc(r)——半径r处的接触压力，Pa；

n——艉轴转速，r/min。

2) 热量分配比的计算。由于动、静环的密封球面温度相等，则有：

(3)

(4)

(5)

式中：q——密封球面总热流密度，W/m2；

h——密封环厚度，m；

λ——密封环的导热系数，W/(m·℃)；

w——动环；

s——静环。

假设：温度场为稳态，对称分布；在工作过程中，摩擦系数保持不变，每个单元面上的热流密度均匀分布。在计算时，将密封静、动环的热流当作边界热流输入来处理。

计算结果表明，静环分配的热流密度qs占密封球面总热流密度q的1%，动环(qw/q)占99%。在ANSYS中加载热流密度时，只须对定义了接触对的2个密封球面分别加载相应的热流密度，即总热流密度乘以分配系数。

3) 对流换热系数。密封环与流体的对流换热系数采用经验公式进行计算。其中静环与周围介质的对流换热系数[12]α为

(6)

式中：λ——介质导热系数，W/(m·℃)，对于海水和空气λ分别为60.85和2.63 W/(m·℃)；

δ——静环与艉管内壁之间的间隙，m，δ=0.2 m；

Nu——努塞尔数，Nu=0.023ε1(Re)0.8×(Pr)0.4；

其中：ε1——修正系数，ε1=1；

Re——雷诺数，Re=2Vδ/v；

V——介质的轴向流速，m/s，V=2 m/s；

v——介质的运动粘度，10-6m2/s，对于海水和空气v分别为1.304×10-6和0.015 53×10-6m2/s；

Pr——密封内腔内介质的普朗特数。

动环与周围介质的对流换热系数[11]为

(7)

式中：λL——介质的导热系数，W/(m·℃)；

D1——动环的外圆当量直径，m；

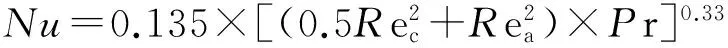
其中：Rec——旋转雷诺数，反映介质的旋转搅拌效应，Rec=ωD2/γ；

ω——动环的角速度，rad/s；

Rea——横向雷诺数，反映介质的横向绕流，Rea=VD/v。

在ANSYS中加载对流换热系数时，即在密封球面外侧分别施加相应的对流换热系数，在其他部位施加20 ℃的恒温边界。

3热-结构耦合有限元分析

当水下航行器艉轴轴线垂向偏移值分别为0、1和2 mm时，为了计算艉轴-球面机械密封耦合模型的总体变形，应用式(1)在艉轴段后端面中心(球心)施加相应的载荷F，以模拟艉轴轴线的垂向偏移値(即球心偏移量)，见图3。

图3 b)中的偏移値S=0.001 195 m，图3 c)中的的偏移値S=0.002 39 m，其结果分别与预期的轴线垂向偏移值1 mm和2 mm基本相等，证明这种模拟方法合理。

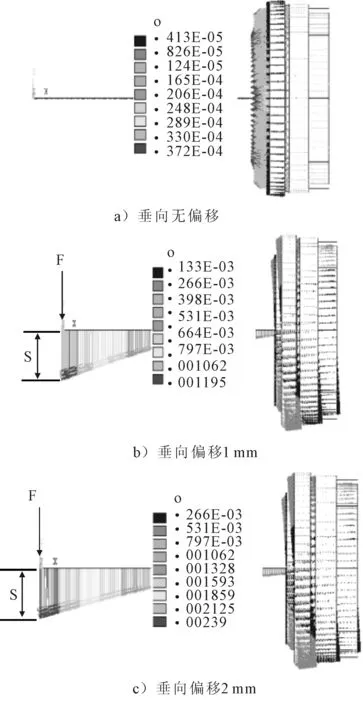
图3　不同偏移情况下耦合模型的总位移

3.1密封球面接触压力

在不同工况和轴线垂向偏移条件下，艉轴-球面机械密封的接触压力会发生变化，直接影响密封球面的变形和温度分布状况。

艉轴轴线垂向偏移分别为0、1、2 mm时的密封球面接触压力峰值见表3。

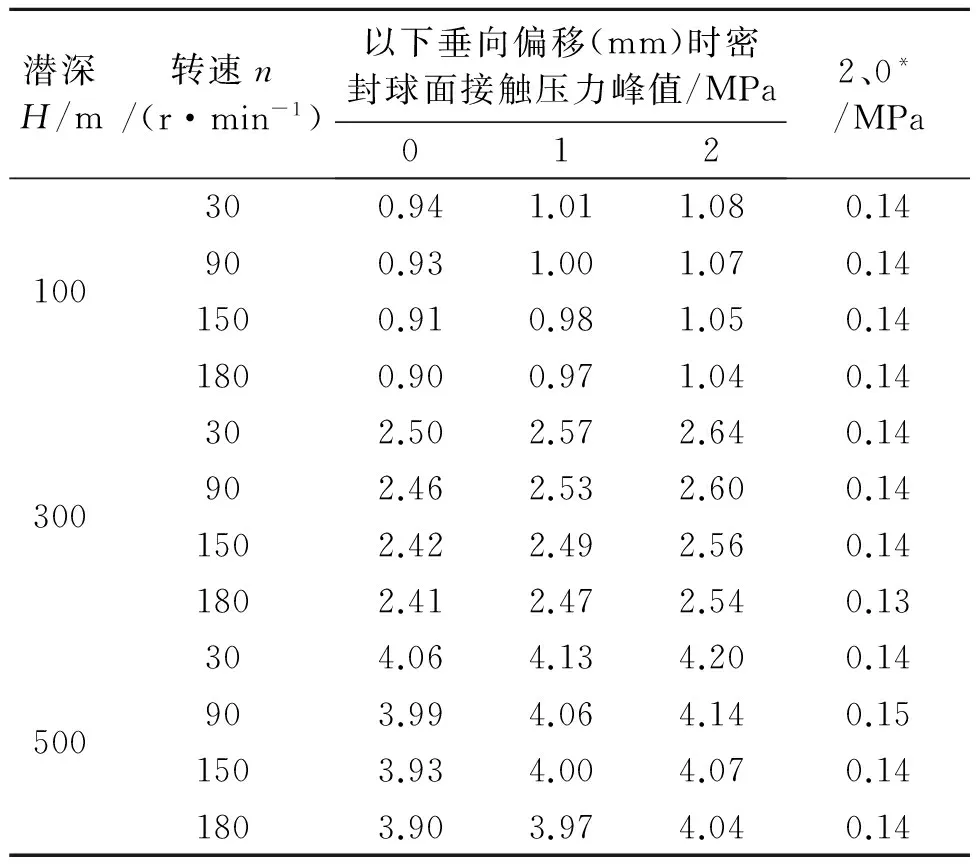
表3　密封球面接触压力峰值

注：*偏移为2 mm和0 mm时的接触压力峰值差值。

由表3可见，在不同工况下，密封球面的接触压力峰值随转速、潜深和垂向偏移的变化趋势一致。

1) 在潜深和垂向偏移不变情况下，球面接触压力峰值随转速的提高而降低。

2) 在转速和垂向偏移不变情况下，球面接触压力峰值随潜深的增加而提高，变化幅度较大。

3) 在不同工况下，球面接触压力峰值随垂向偏移的增加有所增大。从轴线偏移2 mm与轴线无偏移比较可见，在不同的潜深和转速下，球面接触压力峰值增加幅度基本保持在0.14 MPa左右，没有明显波动。这表明球面机械密封具备良好的自适应能力和静环-弹簧系统的快速跟随能力。

潜深为500 m，转速为180 r/min，不同轴线垂向偏移时的密封球面接触压力云图见图4所示。

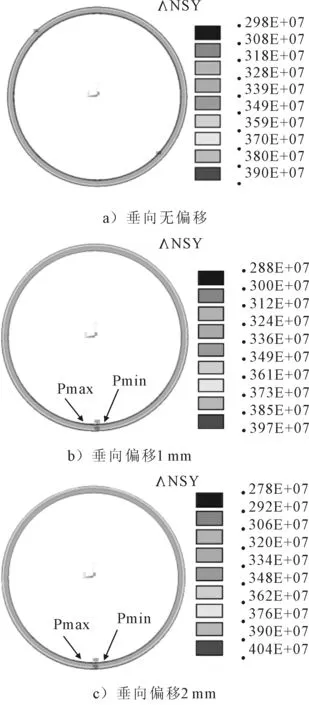
图4　球面面接触压力云图(H=500 m,n=180 r/min)

由图4可见，轴线出现垂向偏移(1、2 mm)后，密封球面最大接触压力pmax和最小接触压力pmin均出现在密封球面正下方，前者在密封球面外侧，后者在内侧。

下面以密封球面的某母线上的节点接触压力来分析该压力沿母线的变化趋势。母线有上、下2段，每段分9个节点，上母线节点为1～9，下母线节点为11～19，上、下母线之间设一无数据节点10，见图5。

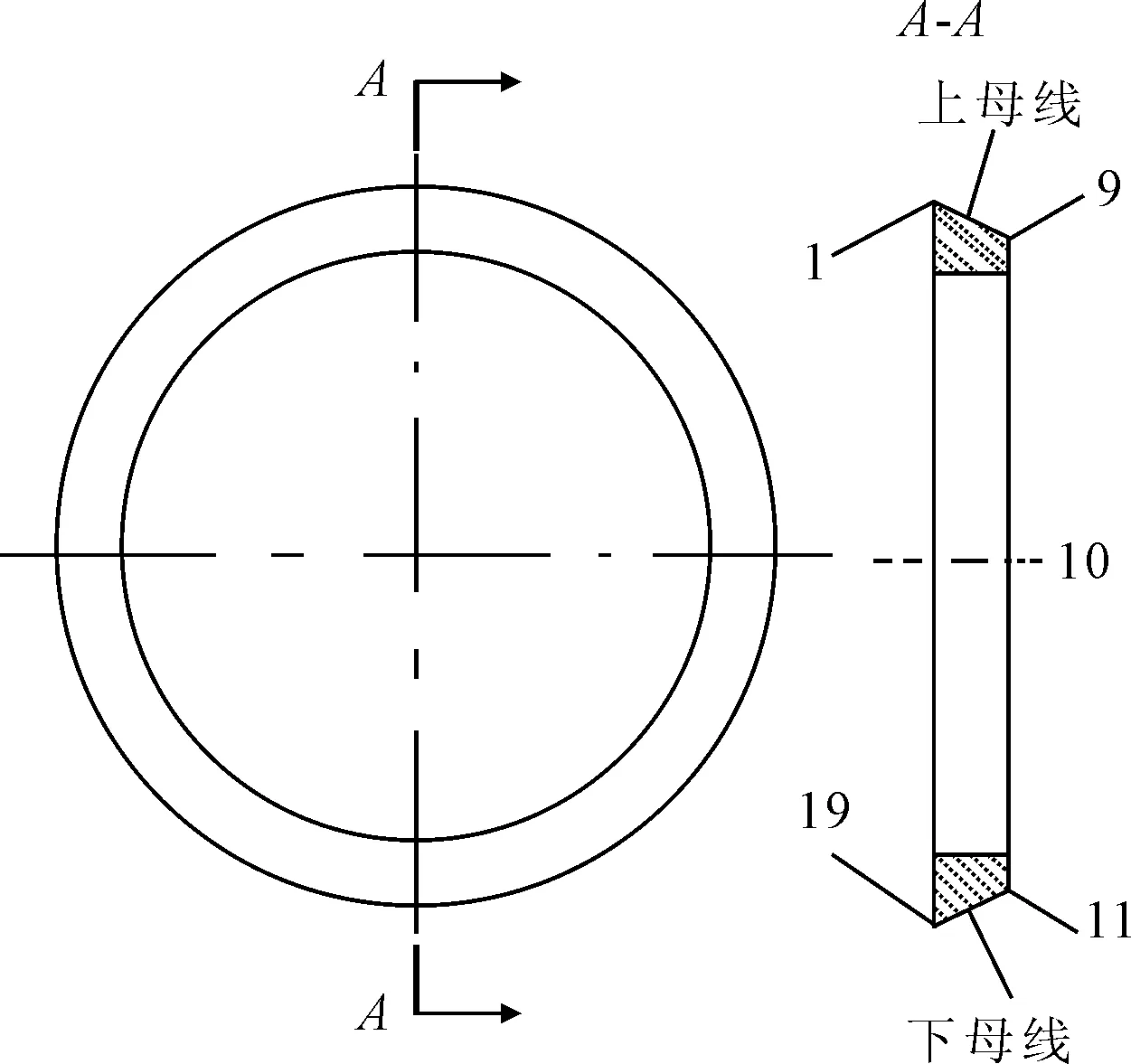
图5　动环-母线上的节点分布

潜深500 m，轴线无垂向偏移和偏移2 mm时，密封球面两母线上的节点接触压力分布状况,见图6。

当轴线无垂向偏移时(见图6a))，上、下母线对应节点(如1-19，2-18，…，9-11)的接触压力相同，转速变化对接触压力没有明显的影响；当轴线垂向偏移为2 mm时(见图6b))，1～9节点和11～19节点的接触压力分布均呈现由外侧向内侧逐渐增大的趋势，但下母线的11～19节点的接触压力与上母线的1～9节点不再呈现对称分布。与无偏移相比，轴线垂向偏移2 mm时的18、19节点接触压力分别高于无偏移的1、2节点，其余节点的接触压力分别小于无偏移的相应节点。

3.2密封球面温度

球面机械密封的密封球面温度分布状况直接影响密封装置的安全性、可靠性。温度过高会导致水膜汽化，引起严重事故，所以应在各种工况下，对密封球面的温度分布状况及其峰值进行分析计算，结果见表4。

表4　密封球面温度峰值

注：*偏移为2 mm和0 mm时的球面温度峰值差值。

由表4可知：

1) 当潜深和轴线垂向偏移不变时，密封球面温度峰值随转速的提高而增大。这是由于转速的提高增大了热流密度所致。

2) 当转速和轴线垂向偏移不变时，密封球面温度峰值随潜深的增加而增大。潜深的增加意味着海水压力上升，增大了密封球面的接触压力，提高了热流密度。

3) 轴线垂向偏移对密封球面温度峰值的影响不大。由轴线偏移2 mm与轴线无偏移相比可见，在不同的潜深和转速下，密封球面温度峰值增加幅度≤0.2 ℃(变化率≤0.7%)。最高温度51.3 ℃，低于密封环材料的极限温度和水膜汽化温度(100 ℃)。这也表明在不同工况下，密封球面的温度变化很小，球面机械密封具有较好的自适应能力以及动、静环间的良好跟随性。

潜深H=500 m、转速n=180 r·min-1和轴线垂向偏移分别为0，1，2 mm时的动环球面温度分布状况见图7。

由图7可见，在不同轴线垂向偏移条件下，动环的球面温度分布都比较均匀，但整个环形分布区域明显出现8条等长圆弧段，这是均布在静环座上的8根弹簧作用的结果。

3.3密封球面变形

在不同的工况及艉轴轴线垂向偏移情况下，动、静环的轴向总变形会发生变化。以转速为180 r·min-1，潜深为100、200、300、400及500 m，球心偏移为0、1、2 mm为例，探讨这3个参数对动、静环轴向总变形的影响规律，见图8。

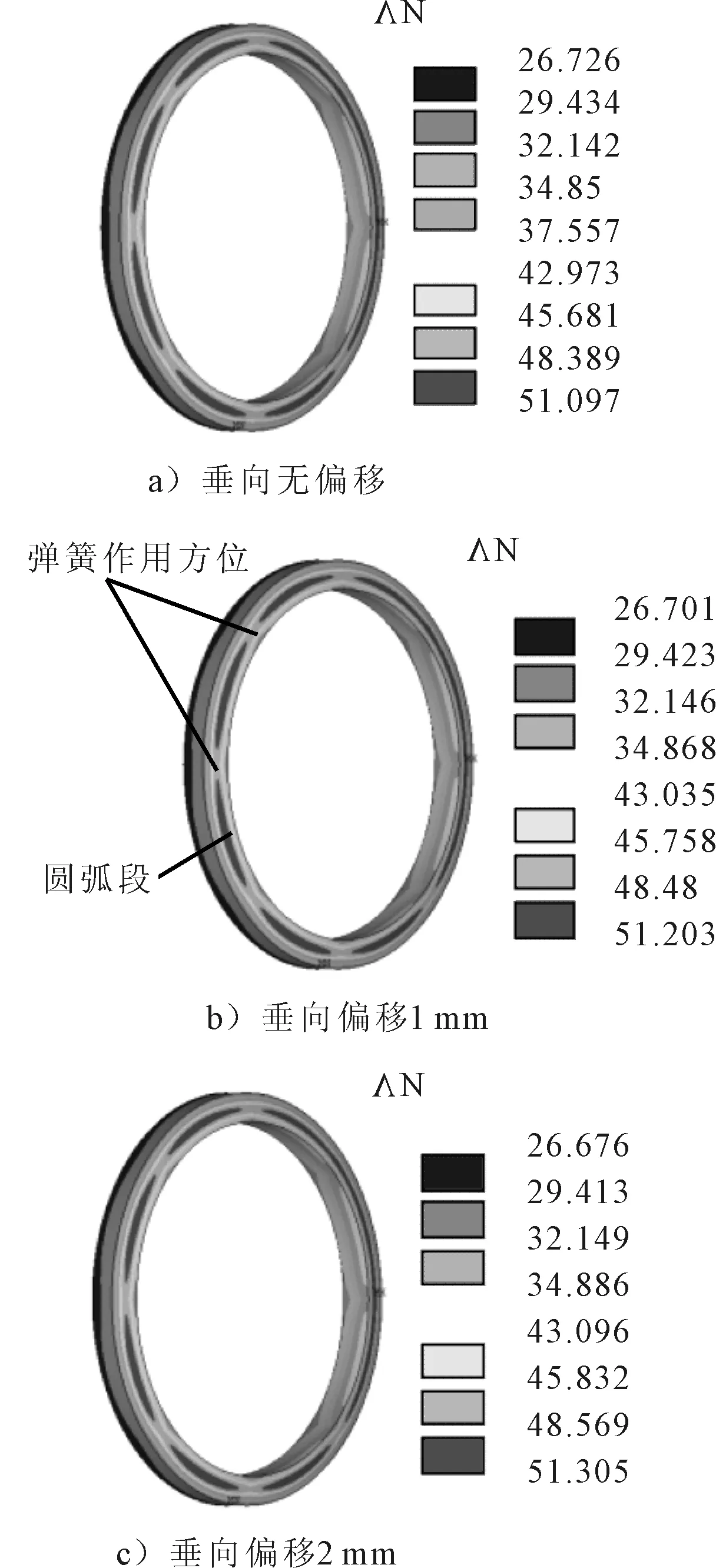
图7　动环球面温度峰值(H=500 m,n=180 r·min-1)

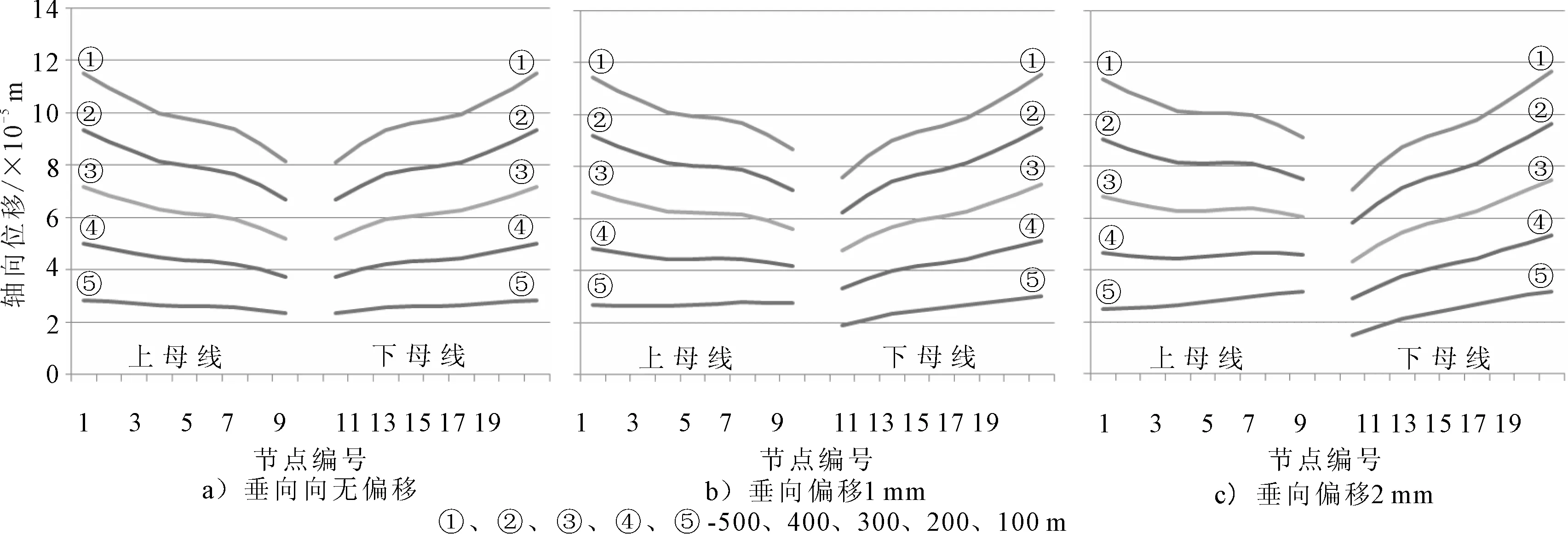
图8　动、静环轴向总位移(n=180 r/min)

由图8可见，动、静环各节点的轴向总变形随潜深的增大而增大，外侧节点的变形大于内侧节点，表现为内锥旋状。变形是由于机械力和热力综合作用的结果，这是导致接触压力峰值出现在接触球面外侧的原因之一。

当艉轴轴线无偏移时，密封环上、下母线(如图8a))的对应节点的变形相同；当轴线有垂向偏移(如1、2 mm)时，上、下母线的对应节点的变形不对称，下母线的外侧节点变形略大于上母线的相应节点，但靠近内侧节点的变形减小，并小于上母线的相应节点，密封环出现朝艉轴后端倾斜趋势。轴线偏移量越大，这种趋势越明显(见图8b)、图8c))。这说明球面机械密封具有良好的自位能力，其静环在弹簧力的作用下对动环拥有较好的跟随性。

4结论

1) 艉轴轴线垂向偏移对球面机械密封的接触压力峰值和温度峰值影响不大，但潜深、艉轴转速的影响较为明显。

2) 动、静环密封面各节点的轴向总变形随潜深的增加而增大，外侧节点的变形大于内侧，表现为内锥旋状。当轴线有垂向偏移时，上、下母线的对应节点的变形不对称，下母线的外侧节点的变形略大于上母线的相应节点，但下母线靠近内侧的节点变形减小，并小于上母线的相应节点。

3) 在轴线有垂向偏移的情况下，密封球面的接触压力、温度和变形与无偏移相比变化很小，说明球面机械密封具有良好的自位能力，能在不同工况条件下保持较稳定的密封性能。

由于球面机械密封的密封面形状与平面机械密封不同，因此还须就密封面形状(如球面半径、密封宽度等)对摩擦振动、泄漏量等的影响状况进行深入的分析与探讨。

参考文献

[1] 林清龙.船舶艉轴机械密封振动与热-热应力研究[D].镇江：江苏大学，2012.

[2] 张振国,姚世卫,王隽.潜艇大深度艉轴密封装置摩擦副机械变形研究[J].船海工程，2004(6):12-14.

[3] 陈德才,崔德容．机械密封设计制造与使用[M]．北京：机械工业出版社，1993.

[4] 成大先.机械设计图册：第4卷[M].北京：化学工业出版社，2000.

[5] CRISTOPHE MINET. A deterministic mixed lubrication model or mechanical seals[J]. Journal of tribology,2011,133:1-13.

[6] NAOTO HIKIDA, HIROYUKI TORIGOE. Study on the reliability improvement of a mechanical seal for the primary loop recirculation pumps (plr pump)[C]. Proceedings of the ASME 2013 Power Conference POWER2013,2013, USA, Boston:1-12.

[7] 赫晓光,王隽,杨俊，等.船舶艉轴机械密封试验装置的设计及密封试验[J].润滑与密封，2010,35(2):94-97.

[8] MINET C, BRUNETIE`RE N, TOURNERIE B, et al. Analysis and modeling of the topography of mechanical seal faces. tribol[J]. Trans, 2010,53:799-815.

[9] MONICA TOMA, JONATHAN LUNTZ, DIANN BRE. Design and proof-of-concept validation of a latched arch active seal[J]. Journal of mechanical design,2012,134:1-12.

[10] WU Dazhuan, JIANG Xinkuo, YANG Shuai. Three-dimensional coupling analysis of flow and thermal performance of a mechanical seal[J]. Journal of thermal science and engineering applications,2014(6):1-9.

[11] 魏立保,陈有光.自润滑关节轴承的研制与应用[J].轴承,2008(5)：8-10.

[12] 朱学明.机械密封性能的数值分析及优化研究[D].武汉：武汉理工大学，2005.

Thermal-structure Coupling Analysis of and Spherical Mechanical Seal of Stern Shaft in Underwater Vehicle

ZHOU Xu-hui, LIU Zheng-lin

(School of Energy and Power Engineering, Wuhan University of Technology, Wuhan 430063, China)

Abstract:The poor shafting-alignment, bearing wear and so on factors in vessels can lead to the plane mechanical seal face of a stern shaft to arouse vertical excursion which can seriously affect the sealing performance such as the contact pressure, temperature and deformation of sealing surface. In order to solve this problem, the research on a spherical mechanical seal is carried out. The finite element method is used to establish the thermal-structure coupling model of the spherical mechanical seal of stern shaft in an underwater vehicle. Under the different depth water and the shaft rotary speed, the influence of the axis vertical excursion on the contact pressure, temperature and deformation of spherical mechanical seal is researched to provide theoretical support for the design and engineering application of spherical mechanical seals. The research results show that under axis vertical excursion, the contact pressure, temperature and deformation of spherical sealing surface are much lower than ones of no vertical excursion respectively, which indicates that spherical mechanical seal is of a good ability of self-aligning and can remain the relative stability of sealing performance under different working conditions

Key words:spherical mechanical seal; thermal-structure coupling model; contact pressure; temperature; excursion

DOI:10.3963/j.issn.1671-7953.2016.03.015

收稿日期：2015-10-08

基金项目：国家自然科学基金(51379168,51139005)

第一作者简介：周旭辉(1978—)，男，博士生，高工 E-mail:zhou719303@163.com

中图分类号：U664.2

文献标志码：A

文章编号：1671-7953(2016)03-0063-07

修回日期：2015-11-23

研究方向:船舶推进系统性能优化