层状地基上核电结构抗震分析与应用
2016-07-04李建波李志远林皋
李建波 李志远 林皋
摘要:基于积分变换、对偶方程与精细积分算法求解多层地基任意形状刚性基础的动力刚度,构建频域框架内的地基动力分析模型,以MATLAB为平台开发了相关软件。利用子结构法在对某百万千瓦级大型核电站进行了结构一地基相互作用分析,得到了该厂房的楼层反应谱。数值算例验证了动力刚度算法的准确性、可行性与工程适用性,对于复杂层状地基上的核电抗震设计具有指导意义。
关键词:层状地基;动刚度;核电抗震;楼层反应谱
中图分类号:TU352 文献标识码:A 文章编号:1000-0666(2016)01-0028-06
0 引言
核电以其清洁高效的特点,在我国的能源发展规划中占有重要地位。核电从诞生之初,其安全性就成为了决策层最关注的问题,核电设计也一直秉承“保守决策”的原则(孔宪京,林皋,2013)。我国是一个多地震的国家,地震活动频度高、强度大、次生灾害多,在核电安全设计中,抗震安全设计就显得尤为重要。另一方面,随着城市化、工业化的飞速发展,促使核电站建设不得不转向内陆地区。内陆地区完整的、稳定性好的岩基日益稀缺,大多为复杂的层状地基,而且地基的层状特性对核电结构的动力反应有重要影响,求解时应加以考虑。但是我国的核电规范中并没有明确地给出如何考虑层状地基动力响应的方法。复杂层状地基上的核电反应分析模型的研究,对于保障核电工程结构的“可靠与安全”有着重要的意义和工程应用价值。
地基-结构体系在地震作用下的反应计算,基本有两种方法:直接法和子结构法。直接法是将地基和结构作为一个总的体系进行分析,地基和结构之间的相互作用直接包含在计算系统内。直接法最大的优点是可以在计算模型中考虑实际地基的复杂情况及其非线性性质。直接法的缺点在于必须截取有限的部分进行分析,边界的引进会造成实际上不存在的波的反射。这使得采用直接法需要复杂的边界处理,在保证精度的同时需要耗费大量的计算时间和费用。
子结构法将总的地基一结构体系分解为几个子结构体系,对各个子结构在频域中进行求解,根据子结构之间边界面的相容条件,将子结构组装成完整体系,得到总的地震反应。本文采用子结构法,将体系分成复杂层状地基和上部结构两部分(蒋通,田治见宏,2009)。上部结构可以通过有限元进行模拟,这样问题的关键就变成了求解复杂层状地基的动力刚度。
Reissner(1936)利用弹性波动理论,对机械基础动力响应做了求解,首先提出了无限地基的动阻抗的求法。随后,Luco和Westmann(1971),Luco和Apsel(1983),Veletsos和Wei(1971)利用积分方程得出了刚性圆盘在竖直、水平作用力和转动、扭转力矩作用下的解析解。这些学者在理论上进行了分析,但是很难应用到实际工程中。近些年许多学者针对层状地基动刚度的计算提出了一些有效的计算模型和求解方法(Park,Kau-sel,2004),但往往在精度和效率两方面不能兼得。
Lin等(2013)提出了一种高精度的混合变量法,该方法对于层状地基有广泛的适用性,且数值求解稳定。混合变量法基于层状地基动力方程的积分变换,结合精细积分算法、对偶波动方程和有限元方法,适用于求解复杂层状地基上明置或埋置基础动力刚度矩阵,应力-位移关系被表示成对偶形式,采用Zhong等(2004)提出的精细积分方法求解,可以达到任意理想的精度。通过混合变量法得到层状地基的动力刚度,利用子结构法可将无限地基的动力刚度加到上部结构的动力分析中,这样可以建立频域内层状地基上的核电结构的动力分析模型。本文首先简要回顾混合变量法,列举典型算例对混合变量法进行验证。其次,以某百万千瓦的核电站为研究对象,采用有限元的模型进行动力学模型模拟。最后通过子结构法将地基动力刚度加到结构刚度上,得到总体的刚度,最后得到关键点的加速度反应谱。本文提供的频域内的层状地基上的核电站的分析模型,对于复杂层状地基上的核电抗震设计具有指导意义。
1 混合变量计算层状地基动刚度
为了充分地利用位移和作用的对称性(Woff,1985),本文选择建立圆柱坐标系。位移函数沿r向做Hankl展开,在环向做傅里叶展开,对位移函数转化得到的频域一波数域进行处理。同时,在地表采用圆形微元建立层状地基的格林影响函数,可使问题得到简化。圆柱坐标系下波动方程的表达式如下:式中,θt为体积应变;ω'r、ω'2和ω'z为位移的转动分量。对于层状地基频率一空间域内的动力响应分析,一种较好的途径就是将Hankel变换到频率-波数内。频率-波数域和频率-空间域之间的Hankel变换定义为利用Hankel正变换可以得到层状地基频率波数域内的波动方程统一形式为其中系数矩阵由层状地基的材料属性确定。利用精细积分算法求解方程(3),可以得到频率一波数域内层状地基内部点的格林函数,在柱坐标系下利用Hankel反变换即可得到频率空间域内圆形均布荷载作用下的格林函数:其中,θ为接受点和激励点水平面上的夹角;Pi和△r分别为圆形均布荷载的幅值和半径;Fij(0,k,z,ω)为频率-波数域内层状地基内部点的格林函数。
定义[Hp]为荷载在笛卡尔坐标系和圆柱坐标系下的转换函数,[N]为转换函数,Fu为计算得到的格林影响函数。将任意形状刚性基础与地基的交界面离散化为一系列圆形微元,利用频率一空间域的格林影响函数建立其平动与转动动力刚度的矩阵方程:
2 层状地基-结构动力相互作用分析
定义结构基础的位移{Uo(ω)},上部结构绝对位移{Ub(ω)}和作用在基础底板的激振力{Fs(ω)}。则上部结构的运动方程可写为:式中,{Sij(ω)}为基础和上部结构的动力刚度矩阵,脚标o,b分别表示基础和上部结构,脚标s表示接触面。在自由场运动作用下无质量基础的反应,工程上一般称为基础的输入运动。求解驱动力可以看成是先求解在地震波入射下为使基础不发生运动需要施加的广义约束,然后计算在解除约束后基础的运动。[K(ω)]为地基的动力刚度矩阵,设广义约束为{F*f(ω)},则基础位移可表示为求解上述方程即可得到频域中的基础反应{Uo(ω)}和上部结构的反应{Ub(ω)}。
3 刚性方形基础置于层状半无限弹性地基动刚度
将边长为2b×2b的刚性方形基础置于层状半无限地基之上。均质半无限地基之上是厚度为b的弹性薄层。底部半无限地基和弹性层剪切波速之比取为CSR/CSL=1.25,密度比为ρR和ρL=1.13,泊松比均为0.33,两者材料阻尼比分别取为0.05和0.03。计算得到的水平、竖直、摇摆和扭转动力刚度矩阵系数按照公式(9)转化为无量纲阻抗函数的形式,其实部(Re)和虚部(Im)的值见图1。将求得的计算结果与wong和Luco(1985)根据积分方程求解的格林函数计算获得的结果进行对比。由图1可见,基于混合变量求得的结果与wong和Luco(1985)的结果吻合得很好,只在高频段有微小的差别,表明该算法可以取得十分精确的结果。
4 复杂层状地基上某百万千瓦级核电站楼层反应谱
4.1 多层场地的动力刚度
场地上部结构基础为宽度为50m,长度为60m的矩形。地基共包含5层不同的材料。每一层的材料属性及层厚见表1。通过混合变量法,计算得到刚性基础的水平、竖直、摇摆向和转动向的动力刚度(图2)。
4.2 反应谱对比
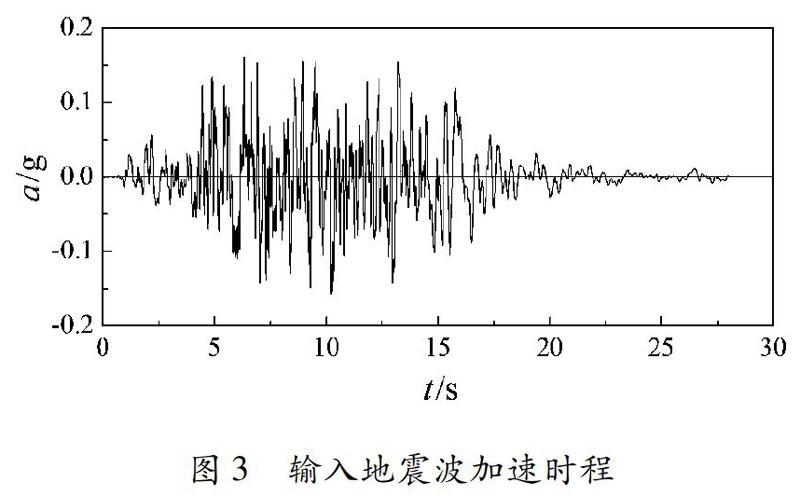
在计算过程中采用的地震波的加速度时程曲线见图3。输入位置为基岩底部。分别计算3种不同计算模型的加速反应谱。本文给出关键点处的反应谱,反应谱对比见图4。
5 结论与讨论
本文基于层状地基的混合变量的精细化算法,得到了层状地基的动力刚度矩阵。通过与wong和Luco(1985)得出的计算结果对比,可以验证混合变量法的准确性。混合变量方法与边界元传递矩阵算法等相比,对任意各向同性层状地基具有广泛的适用性,对地基的厚度、弹性地基材料属性没有任何限制;此算法基于矩阵数值计算,数值求解稳定。利用子结构法,将复杂的层状地基的动力刚度与核电上部结构的刚度合成总动刚度,分成3种不同的连接方式,并得到了上部结构的加速度反应谱。本文建议的频域内的核电厂房分析模型,可以考虑层状地基对结构动力响应的影响,这对保障核电工程结构的“可靠与安全”具有重要的理论意义和工程应用价值。