分布式光伏发电接入对配电网谐波特性的影响*
2016-07-04叶琳浩黄伟张勇军
叶琳浩 黄伟 张勇军
(1.华南理工大学 电力学院, 广东 广州 510640; 2.广东电网有限责任公司佛山供电局, 广东 佛山 528000)
分布式光伏发电接入对配电网谐波特性的影响*
叶琳浩1,2黄伟2张勇军1
(1.华南理工大学 电力学院, 广东 广州 510640; 2.广东电网有限责任公司佛山供电局, 广东 佛山 528000)
摘要:为研究分布式光伏发电并入配网对谐波特性的影响,建立简化的配网模型进行理论分析,考虑了电缆电容和无功补偿装置对系统响应特性的影响,背景谐波采用工程实际应用较多的恒流源模型,基于Digsilent搭建实际的分布式光伏发电接入的配网模型,研究了PV接入方式、电容的系统响应特性变化对配电网谐波的影响.仿真分析表明:特定的网架结构会相应放大某一次或某几次谐波,使谐波畸变的严重程度超出系统承受范围;优化PV的接入位置和分散度方式、改善滤波通道等方法可降低配网的波形畸变水平.
关键词:配电网;可再生能源;分布式光伏发电;谐波畸变
以石油、煤炭、天然气为主的化石能源逐渐走向枯竭,为应对能源危机,各国政府纷纷将风力发电、光伏发电等可再生能源的发展提上战略议程.我国《能源发展战略行动计划(2014-2020年)》提出“绿色低碳”的发展战略,拟将2030年非化石能源占比提高到20%左右.
对于可再生能源极度丰富的地区可采用集中式发电,接入到110 kV电网;对于资源相对匮乏的地区则适合发展分布式发电,接入35 kV及以下的中低压配网.光伏屋顶、家用小风电都属于分布式可再生能源,其接入配网将会改变配网的电源结构,对配网产生较为复杂的影响.大部分可再生能源需要经过电力电子装置转换成标准的工频电流才能并入系统,因此向电网注入谐波是不可避免的[1].注入的谐波不仅会对加速老化配网中的变压器、电容器、电缆等设备,增加额外损耗,还会增大对波形质量较敏感的企业用户的生产误差,使企业蒙受不必要的损失.
分布式光伏发电是目前最具开发潜力的可再生能源发电技术之一,产生谐波较多,文中以文献[2- 3]中描述的三相光伏逆变电源作为研究对象分析可再生能源接入对配网谐波特性的影响.然而配网网架结构的复杂性及光伏接入位置及方式选择多样性[4]给配网谐波分析带来了很大的挑战.文献[5]中建立了电力电子装置和配电网的模型,对含分布式电源配电网的谐波特性进行了详细的分析,但其主要考虑理想状态下高次谐波的影响而选择忽略低次谐波.文献[6]中对线性模型、非线性模型分布式电源分别在理想配电网系统中进行了研究,但未考虑实际配网中电缆对地电容的影响.文献[7]中基于PSCAD/EMTDC平台搭建了光伏并网模型,模拟不同接入条件下光伏并网对配网谐波的影响,根据负载容量优化了接入位置,然而其用于仿真的配网网架结构简单,仅有一个分支且距离较短,均为架空线路,不能体现实际配网分支负荷分布对整体的影响以及高电缆出线的电容特性对谐波的影响.
文中选取实际型号的逆变器模拟光伏系统(PV),基于IEC61000标准建立PV的谐波源模型,基础数据来自逆变器出厂测试数据.通过改变PV的接入方式、位置等因素来详细分析可再生能源接入对配网的谐波特性影响.
1谐波分析方法
太阳能发电要通过光伏逆变器并网,因而会向配电网注入大量谐波电流,引起各节点电压畸变.
引起畸变的大小与PV接入的容量及位置有关,为简化分析,设计了一个简单的单辐射馈线配网系统,如图1所示.
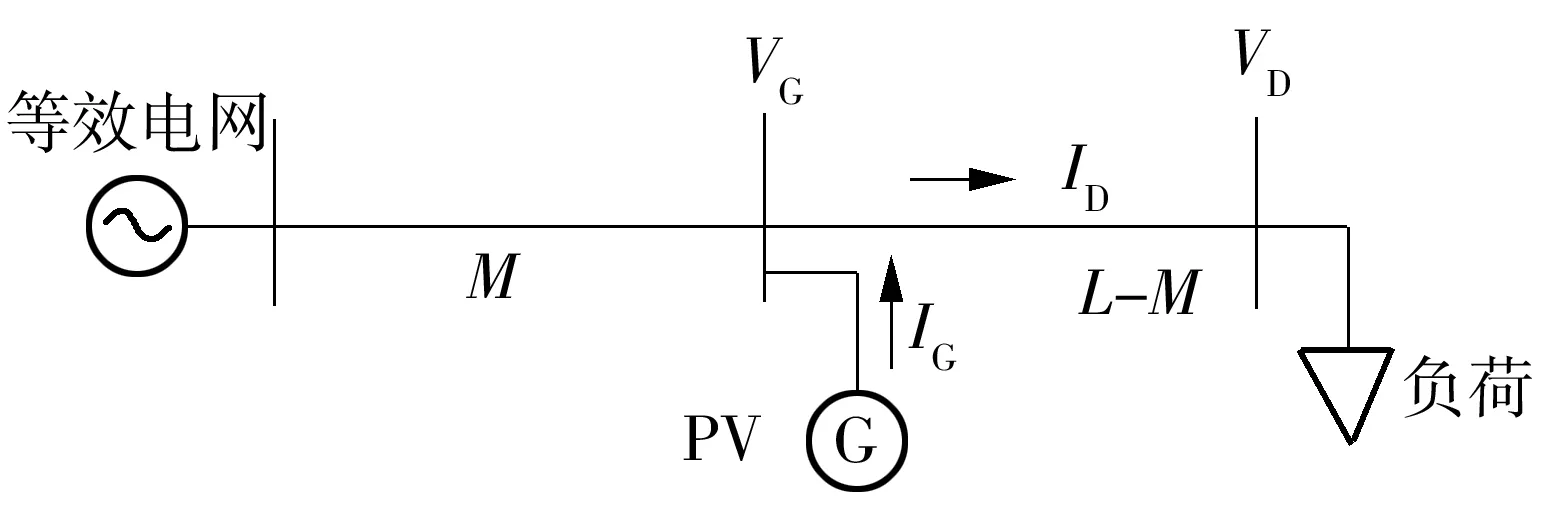
图1 PV接入配网图
图中,M为等效电网母线到PV的距离;L为负荷到等效电网的距离;VG为PV并网点的电压幅值;对照图1,下文中,δG为PV并网的电压相角;PG为PV输出的有功功率;QG为PV输出的无功功率;cosφG为PV的功率因数;φG为PV的功率因数角;VD为负荷节点的电压幅值;PD为负荷消耗的有功功率;QD为负荷消耗的无功功率;cosφD为负荷消耗的功率因数;输电线的单位阻抗设为r+jx,单位电纳设为b.
1.1谐波源模型
电力系统中多数谐波潮流分析是用线性稳态电路的处理技术进行求解.谐波源是一种非线性元件,通常认为是往线性网络模型注入谐波的注入源,可分为电流源和电压源.目前工程实际应用中将逆变器和负荷中非线性负载看做是内阻无穷大的谐波恒流源,便于对多个无规则谐波源进行叠加计算,正适合于文中对多个谐波电流经过线路传输后对各节点波形畸变的影响研究.
通常,配电母线上的电压畸变相对较低,因此在供电系统中可以认为逆变器及非线性负载的电流畸变是相对恒定和独立的畸变,即认为谐波源所产生的谐波电流仅取决于设备的出厂频谱特性.
(1)
(2)
式中:Ih、θh为h次谐波电流的幅值和相角;I1、Imeah、Imea1分别代表实际基波电流、h次谐波测试电流、基波测试电流;θ1、θmea1、θmeah分别为基波电流相角、基波电流测试相角、h次谐波测试相角;各次谐波电流含量水平可以由文献[9]或从设备出厂测试报告获取.恒流源模型在多谐波源叠加问题方向应用广泛,因而非常适合文中分布式光伏电源并网的研究.
1.2未接入光伏时的谐波分析
常规的配网负荷属于非线性负荷,本身也是一个谐波源.在PV接入之前,注入各节点的谐波电流仅与流入负荷的基波电流幅值和相角成线性关系.假设负荷电流的第h次谐波用其幅值与基波电流幅值的比值表示,记为IDinh,流入负荷的基波电流幅值为
(3)
第h次谐波的注入电流为
(4)
系统等值网络如图2所示.

图2 PV未接入配网模型图
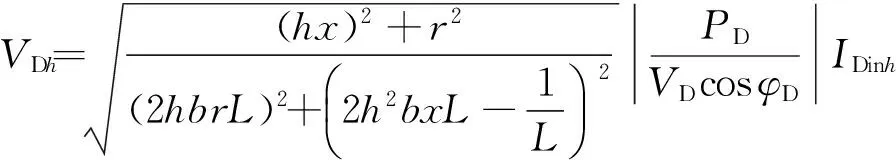
(5)
式中,r、x、b均为线路的单位电阻、电抗、电纳,对于同一型号的线路取常数值.当谐波次数h变化时谐波电压也会变化,因此不同次数的谐波经过同一线路其影响特性也不同.由于电缆线路的单位导纳较大,因此即使是配网较短的线路也不可忽略其对地电容的影响.不同的线路型号和长度会对应一个特定的h,使VDh有一个极大值,可以看做是线路对特定次数谐波的放大作用.
2PV接入对谐波的影响分析
从PV流出的基波电流IG的幅值为
(6)
PV注入电流的第h次谐波用其幅值与基波电流幅值的比值表示,记为IGinh.h次谐波注入电流幅值为
(7)
h次谐波注入电流相角为
θGh=θGih+h(δG-φG)
(8)
假设PV的第h次谐波的电流相角θGinh为0,而PV的功率因数接近于1,所以φG很小,接近于0.又因为配网线路较短,且线路r/x较大,所以δG接近于 0,因此θGh为0.同理,负荷的第h次谐波注入电流相角也为0.线路末端负荷节点的第h次谐波电压幅值可以表示为
(9)
接入PV后系统的等值模型如图3所示.

图3 PV接入后配网模型图
通过对比式(5)与(9),可以得出接入PV后,线路末端节点的h次谐波电压幅值变化,即

(10)

①接入点之前的线路
假设在接入点之前某一位置Z(Z (11) PV一般不参与电压调节即为恒功率模型,由电压质量分析已知,接入位置增大,VG也增大,IGh随之减小.同理,随着接入位置M增大,沿线压降减小,末端电压就增加.由式(2)可知,当末端电压增大时,IDh就会减小,因此式(11)中的VZh就会减小,电压畸变幅度降低. ②接入点之后的线路 假设在接入点之后的某个位置Z,Z>G,则该点的第h次谐波电压幅值可以表示为 (12) 由式(12)可以看出,虽然电缆线路的b值相对较大,但数量级仍然很小,在谐波次数h较小的情况下,接入位置M增大,(2hbrM)2+(2h2bxM-1/M)2整体减小,相应次数的谐波电压增大;h较大时,注入的谐波电流IGh又很小,相应次数的谐波电压畸变的增加对总电压畸变影响较小.因此,当接入位置M增大时,接入点之后的线路电压畸变幅度增加. 3系统响应特性对谐波的影响分析 供电企业为保障客户端的电压质量和提高供电可靠性,在城农网改造时逐步完善了10 kV配电线路中的无功补偿装置.长支路的感抗加上补偿电容的容抗恰好形成一个串联电抗电容的支路如图4所示.为方便分析谐波相应特性,此处忽略电阻的作用. 图4 含支路补偿电容等效系统图 Fig.4Equivalent network model with compensation capacitor in branch 图4中,In为第n次谐波电流,XL为支路感抗,XC为补偿器的容抗,XS为系统侧感抗.Inc为流入支路的n次谐波电流,Ins为流入系统侧的n次谐波电流.电感的谐波阻抗与频率成正比,电容的谐波阻抗与频率成反比.因此当谐波次数增大到nx时,发生并联谐振,谐振环流会使得系统中nx次及其附近的谐波电流被放大,相应的谐波电压畸变也会放大.且支路电容越大,nx就越小. 4仿真验证与分析 4.1算例介绍 文中所用的配网模型来自广东某城市配网的一条10 kV链式馈线,馈线是沿着开闭所方向的一条长线路,由开闭所拓展至附近的负荷点.其网架结构和具体参数分别见图5和表1.母线0是10 kV变电站出口母线,母线1-6分别是沿线的6座开闭所.负荷用户主要由学校、商场大厦、居民区组成,负荷变化具有一定的时间特性. 图5 链式馈线结构图 编号线路线路型号长度/km有功/MW无功/Mvar10-1YJV-3001.950.4600.04421-2YJV-3001.281.9050.34232-3YJV22-3×3001.801.3830.25243-4YJLV-2400.250.7250.10454-5YJLV-2400.100.4400.11665-6YJV-1500.470.2190.057 4.2仿真案例说明 分布式光伏电源接入的位置、方式以及负载情况的不同都会引起对配网电能质量影响的不同,故选取几种典型的接入情况作为仿真案例,细节见表2. 选用目前国内市场占有率较高的YG公司生产的0.05 MV·A的光伏逆变器作为分布式光伏电源,其谐波特性参数取自其出厂测试报告,各次谐波最大含有率取三相最大值(见表3). 表2 仿真案例说明 1)表格中的百分比是占最大负荷容量的百分比. 表3 逆变器谐波参数 4.3接入位置对谐波的影响 图6是算例4下的各节点电压总畸变率,可以看出,在不改变谐波源模型、接入方式及接入容量的情况下,分布式光伏的位置越接近系统母线,则线路整体的谐波畸变水平就越低,与文献[7]中的结论一致.但文中最大谐波电压畸变点位于线路末端节点,而文献[7]中的谐波电压畸变最大的节点出现在接入点,这是因为文中考虑到实际配网的负荷中存在非线性负荷,也会向系统注入谐波电流.故校核线路节点电压是否都满足标准时可以直接由线路末端的电压畸变值判断得出结论.接入位置的改变是通过改变基波电压来影响谐波的注入水平.由于接入容量未超过负荷总容量时,沿线电压仍呈下降趋势,即接在首端时接入点的基波电压要高于接入在末端时的基波电压,而对于恒功率模型的光伏电源,基波电压越高,基波电流则越小,因此,光伏电源的接入位置越接近系统母线,整体注入PCC的谐波电流就越小.反之,接入位置越靠近末端,注入PCC点的谐波电流就越大. 图6 不同接入位置下各节点的电压总畸变率 Fig.6Total voltage distortion rate of each node under different access locations 4.4分散方式对谐波的影响 考虑到用户实际需求以及资源分布问题,实际规划光伏等分布式可再生能源时很难将其集中到一个负荷点.当接入容量较大时,通常会分散到各节点接入.对算例5进行仿真,分散方式分别为平均分布,随机分布(电脑随机数产生),按负荷比例分布(该点接入容量与接入总容量之比等于该点负荷与负荷总容量之比)进行仿真,每个并网点接入的逆变器台数见表4,每台逆变器的容量为0.05 MVA,仿真结果见图7. 表4不同分散度下接入容量(台数)信息表 Table 4Access capacity information under different dispersities(set) 接入方式母线1母线2母线3母线4母线5母线6平均接入99991010随机接入1146810126随机接入2121811348按负荷比例接入43014323 图7 不同分散度下各节点的电压总畸变率 Fig.7Total voltage distortion rate of each node under different dispersities 由图7可以看出,平均接入和按负荷比例接入整体的谐波水平要略高于随机接入,这主要由两个原因造成.其一是随机接入接在首端的容量较大,由接入位置分析已知接入位置靠近系统母线可减少谐波的注入水平.另一个原因是每一台光伏逆变电源都可以看作是一个小谐波源,谐波源与谐波源之间的谐波存在叠加关系.当两台谐波源靠的比较近时,相角可能较为接近,呈线性叠加.单点数量较多时,会出现相角正负抵消的情况,谐波注入反而会比更分散的接入方式注入谐波小. 4.5负荷轻载对谐波的影响 由上述分析可知,光伏出力越大,谐波畸变也就越大.以上仿真基于负荷和光伏电源都是恒功率模型,然而实际中的配网负荷和光伏出力都是实时变化的,且变化幅度较大.国标中对注入PCC点的谐波电流及各节点电压畸变率有严格限制,因此必须考虑较为极端的情况,以防止注入的谐波高于国标限值.选择算例2、3、6,仿真结果见图8. 由图8可以看出,重载时馈线的谐波要略高于轻载时的谐波水平,这主要由两个原因造成.其一,负荷本身是一个谐波源,负荷轻载,其注入谐波电流也就较小.负荷谐波电流与逆变器谐波电流相比较小,影响并不大.另一个原因则是负荷轻载时,沿线电压会升高,对于功率一定的光伏电源其谐波基波电流会减小,注入的谐波电流也会相应减小.从整体来看,负荷轻载反而会造成谐波水平有轻微降低,不会恶化谐波水平. 图8 负荷轻载时各节点的电压总畸变率 Fig.8Total voltage distortion rate of each node under light load 4.6电缆电容对系统响应特性的影响 使用算例3进行仿真,谐波源在馈线的末端.先将所有电缆线路的对地电容参数设为0,观察各次谐波的注入电流、线路中段的电流以及注入外网的电流,结果如图9所示. 图9 不计电缆电容时系统的各次谐波 将电缆线路的电容参数设为实际值,各次谐波的注入电流、线路中段的电流以及注入外网的电流如图10所示. 图10 计及电缆电容时系统各次谐波 由图9可以看出,在不考虑电缆电容的情况下,并联谐振点在25次谐波之外,光伏电源的谐波主要集中于2-25次,尤其是11次以下,25次之外的可以忽略,因此当谐振点在25次之外时,对整体的谐波放大作用不明显.当计及电缆的电容时,如图10所示,谐振点明显向前偏移,对14次附近谐波有一个极端放大,由于实际存在的电阻值并非小到可以忽略,因此谐振点的谐波电流是被放大到一定值而非理论上的无穷大.综合图9、10可以看出,PV通过逆变器并入配网会使得配网的偶次谐波不能被忽视,大量注入偶次谐波会严重危害打牌PCC点的上其他出线的用电设备,造成旋转电机、变压器以及电容器的损伤,同时还可能干扰继电保护装置和自动重合闸装置的正常工作.国标[14]中依据PCC点不同的外网短路容量制订了详细的各次谐波电流注入限值及换算公式,以防止过多注入的谐波电流影响配网的安全运行.通常滤波时滤波通道设置在注入谐波较大的频率,然而更高次的谐波在经过系统响应后再被放大,也会对系统造成危害,因此在设置滤波通道时,还应考虑系统的响应特性,调整滤波器的串抗率,让谐振点处在谐波较小的频带内. 5结语 文中在考虑电缆对地电容的影响上建立配网及谐波源的简化模型,对PV接入带来的影响进行了详细的理论推导.通过仿真计算结果的对比,得出如下结论: (1)引入通过电力电子器件并网的可再生能源会明显增加配网的谐波电压畸变水平.特定长度的电缆线路会对对应次数及其附近的谐波产生放大作用,需要安装滤波装置来限制单次过高谐波. (2)接入位置不变时,接入的容量越大,配电网的谐波畸变水平就越高;接入容量不变时,接入位置越靠近线路末端,配电网的谐波畸变水平就越高,最大谐波电压畸变点位线路末端节点.从减小谐波畸变率的角度出发,不宜将可再生能源接入线路的末端,可以考虑接在负荷较重的中部节点. (3)在满足用户的安装需求以及线路载容量的校核后,应尽量控制PV从同一点接入,谐波源之间的相互抵消作用可帮助降低谐波的扩散. (4)当负荷中存在大量非线性负荷时,校核PV接入是否会引起谐波畸变超标时,应考虑到最极端的情况,即负荷水平达到最大. (5)校核谐波畸变时还需考虑周边电网的背景谐波情况,如是否存在冶炼业或牵引站,推荐留有一定裕度,防止配网谐波因周边背景谐波的传递而超标. (6)PV的接入使得配网内的10-25次谐波值不可忽略.设置滤波通道时不仅要考虑谐波的注入特征,还需考虑系统的响应特征,以防某些高次谐波被放大,危害配网安全. 文中目前只考虑了逆变型电源的接入,随着可再生能源的发展,会有更多类型的电源接入配网,多种不同类型的电源接入会对配网谐波产生怎样的交互影响还有待进一步研究. 参考文献: [1]ZHANG J F,DING S M,HANG Y L,et al.Research on distributed generation source placement [C]∥Procee-dings of International Conference on 2009 SUPERGEN’09.[S.l.]:IEEE,2009:1- 4. [2]YE Y,KAZERANI M,QUINTANA V H.Modeling,control and implementation of three-phase PWM converter [J].IEEE Trans on Power Electronics,2003,18(3):857- 864. [3]朱晓亮.基于电网电压定向三相并网逆变器的研究 [D].南京:南京航空航天大学自动化学院,2010. [4]BOMMAREDDY C,MAKRAM E.Power quality studies in the presence of DG [C]∥Proceedings of Power Systems Conference:Advanced Metering,Protection,Control,Communication,and Distributed Resources.[S.l.]:IEEE,2006:224- 229. [5]谢秉鑫,王宗,范士林.分布式电源对于配电网谐波特性的影响 [J].电力系统保护与控制,2012,40(2):116- 119. XIE Bing-xin,WANG Zong,FAN Shi-lin.Influence on harmonic characteristics of distributed network with distributed generations [J].Power System Protection and Control,2012,40(2):116- 119. [6]张俊芳,姚强,杭银丽.分布式电源对配电网谐波分布影响的研究 [J].电气应用,2011(18):61- 65. ZHANG Jun-fang,YAO Qiang,HANG Yin-li.Research on the effects of distributed power harmonic distribution of distribution network [J].Electrical Applications,2011(18):61- 65. [7]徐群.分布式电源并网对电能质量的影响分析与评估 [D].北京:华北电力大学电气与电子工程学院,2012. [8]孙媛媛.非线性电力电子装置的谐波源模型及其在谐波分析中的应用 [D].济南:山东大学电气工程学院,2009. [9]丁明,王伟胜,王秀丽,等.大规模光伏发电对电力系统影响综述 [J].中国电机工程学报,2014(1):2- 14. DING Ming,WANG Wei-sheng,WANG Xiu-li,et al.A review on the effect of large-scale PV generation on power systems [J].Proceedings of the CSEE,2014(1):2- 14. [10]刘伟,彭冬,卜广全,等.光伏发电接入智能配电网后的系统问题综述 [J].电网技术,2009,33(19):1- 6. LIU Wei,PENG Dong,BU Guang-quan,et al.A survey on system problems in smart distribution network with grid-connected photovoltaic generation [J].Power System Technique,2009,33(19):1- 6. [11]廖志伟,蓝鹏昊,崔法聚,等.含分布式电源配电网的继电保护方案 [J].华南理工大学学报(自然科学版),2013,41(12):70- 74. LIAO Zhi-wei,LAN Peng-hao,CUI Fa-ju,et al.Relay protection scheme for power distribution network with distributed generations [J].Journa of south China University of Technology(Natural Science Edition),2013,41(12):70- 74. [12]刘立群,王志新.PV系统的变电压MPPT算法及仿真 [J].华南理工大学学报(自然科学版),2009,37(2):140- 146. LIU Li-qun,WANG Zhi-xin.Variable-voltage MPPT algorithm and simulation of photovoltaic system [J].Journal of South China University of Technology(Natural Science Edition),2009,37(2):140- 146. [13]IEEE Std 519—1993.IEEE recommended practices and requirements for harmonic control in electric power systems [S]. [14]GB/T 14549—1993.电能质量公用电网谐波 [S]. Influence of Distributed Photovoltaic Power Generation on Harmonic Characteristics of Power Distribution Network YELin-hao1,2HUANGWei2ZHANGYong-jun1 (1.School of Electric Power, South China University of Technology, Guangzhou 510640, Guangdong, China;2.Foshan Power Supply Bureau, Guangdong Power Grid Corporation, Foshan 528000, Guangdong, China) Abstract:In order to investigate the influence of distributed photovoltaic power generation on the harmonic characteristics of power distribution networks, a simplified model for the theoretical analysis of power distribution network is established, which considers the influences of cable capacitance and reactive power compensation device on the system response characteristics. Next, an actual distribution network model based on Digsilent is constructed by using the constant-current source model commonly used in engineering practice as the harmonic source model, and the model is then used to reveal the harmonic characteristics affected by the PV access mode and the system response characteristics of capacitance.Simulated results show that specific grid structure may amplify the harmonic and cause excessive waveform distortion, and that the distortion level can be decreased by optimizing the access location and dispersion of PV and by improving the filtering channels. Key words:power distribution network;renewable energy; distributed photovoltaic power generation; harmonic distortion 收稿日期:2015- 06- 24 *基金项目:国家自然科学基金资助项目(51377060);华南理工大学中央高校基本科研业务费专项资金资助项目(2013ZM0013) Foundation item:Supported by the National Natural Science Foundation of China(51377060) 作者简介:叶琳浩(1983-),男,博士生,现任职于广东电网有限责任公司佛山供电局,主要从事电力系统优化运行与规划研究.E-mail:77329615@qq.com 文章编号:1000- 565X(2016)04- 0084- 07 中图分类号:TM 401+.1;TM 615 doi:10.3969/j.issn.1000-565X.2016.04.013