基于Gabor滤波器的Graph Cuts右心室MR图像分割

马　双　陆雪松

(中南民族大学生物医学工程学院　武汉　430074)

基于Gabor滤波器的Graph Cuts右心室MR图像分割

马双陆雪松

(中南民族大学生物医学工程学院武汉430074)

摘要在医学图像处理中,右心室分割在临床医学诊断和对病情的定量分析中有着越来越重要的意义。由于心脏MR图像右心室具有高变异、壁薄、边界不明显的特点,论文利用2D-Gabor对心脏图像进行滤波处理,得到特征图像,借助高斯混合模型融入到Graph cuts算法中,完成右心室MR图像的分割。相比于经典算法,该方法在稳定性及准确率上都有较好的效果。

关键词2D-Gabor; Graph cuts; 右心室分割

Class NumberTP391.4

1引言

一直以来,心血管疾病严重威胁着人类的健康,快速有效的心血管疾病诊断方法在临床上具有重要的意义。最近的研究发现,右心室的功能不全与心脏衰竭、右心室心肌梗死等疾病的诱发有较大联系[1],由此引发人们对右心室的功能评价产生更多的关注。磁共振成像以其独特优势已经逐渐成为右心室评价的标准工具,对心脏磁共振图像的分割也成为医学图像处理的热点。然而,由于心脏MR图像中右心室的高变异、壁薄和边界不明显等特点,使其成为心脏分割中的一大难点。

Elbaz等[2]用一种新的主动形状模型(Active Shape Model,ASM)和间剖面模型分割右心室,这种方法比经典的ASM精度更高。Mahapatra[3]利用上下文信息结合左右心室的几何关系分割两个心室,提高了分割的精度,同时对噪声有很好的鲁棒性。刘复昌[4]等基于图划分的主动轮廓方法,实现了形状统计主动轮廓模型来分割心脏MR图像,解决了边缘泄露的问题。最近MICCAI 2012 RV(Right Ventricle)分割的挑战中,Zuluaga[5]等使用多标签融合实现了右心室的自动分割。以图割方法为基础,Nambakhsh[6]等使用凸松弛和分布匹配,在不动点方程的基础上,实现了尺度不变性的三维图像快速分割。Grosgeorge[7]使用统计主成分形状先验,解决右心室与周围组织对比度地和高形状变异的问题。Maier等[8]先进行人工标记前景和背景的轮廓,然后使用分水岭方法粗略分割出这些区域,最后通过图割的方法来精确分割四维右心室图像。

本文利用2D-Gabor所描述的图像边缘特性,将其融入Graph Cuts中进行右心室MR图像分割,拟克服图像中边界不明显和对比度低的难题。

2传统Graph Cuts算法

Graph Cuts算法最初由Boykov[9～11]等在2001年提出,在计算机视觉领域普遍应用于前背景分割、立体视觉和抠图等。它将图像分割问题与图的最小割问题进行关联。首先用一个无向图G=〈V,E〉表示要分割的图像,V和E分别为顶点和边的集合。与普通的图不同的是,Graph Cuts图是在普通图的基础上多了两种顶点,分别用符号“S”和“T”表示,其它所有的顶点都必须和这两个顶点相连形成边集合中的一部分。Graph Cuts中的边分为两种:一种是普通顶点与相邻顶点的连接,这种边叫n-links;另一种是普通顶点与S或T之间的连线,这种边叫t-links。一个cut就是所有边集合E的一个子集,该集合中所有边的断开会导致残留“S”和“T”图的分开,所以就称为“割”。如果一个cut,它的边的所有权值之和最小,那么这个就称为最小割,也就是图割的结果。Graph Cuts分割示意图如图1所示。

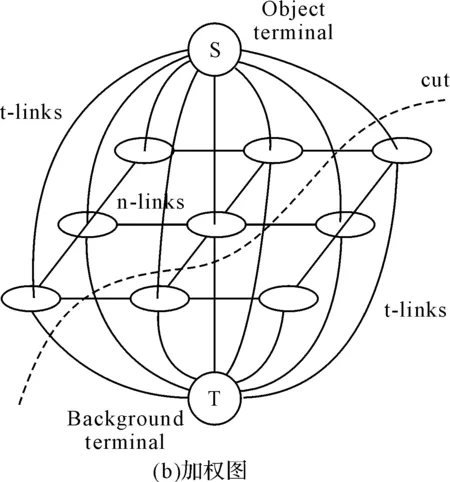
图1　对3*3图像Graph Cuts分割的简单实例

图割的能量函数[11]可以表示为

E(L)=λ·R(L)+B(L)

(1)

(2)

(3)

L={l1,l2,…,lp}为整幅图像的标签,其中li为0表示背景,1表示目标。R(L)为区域项,B(L)为边界项,而λ就是区域项和边界项之间的重要因子,决定它们对能量的影响大小。如果λ为0,那么就只考虑边界因素,不考虑区域因素。在计算t-links时,经典Graph Cuts往往使用统计直方图的方法获取样本的概率密度函数。设x={x1,x2,…,xn}为前景的训练样本,对它们进行直方图统计,以此估计测试样本X属于前景的条件概率P(X|O),同理得到背景的条件概率P(X|B),然后使用贝叶斯公式:

(4)

得到前景的后验概率,P(O)和P(B)为前景和背景的先验概率。

3改进的Graph Cuts算法

为了克服使用统计直方时目标过分割或欠分割的问题,本文利用Gabor滤波器来提取具有边缘特性的多维特征,采用高斯混合模型来计算前景或背景的后验概率。

3.12D-Gabor滤波器

Gabor滤波器是一个用于边缘检测的线性滤波器。为了得到心室的边缘特性,本文使用了Gabor滤波器对心室图像进行了处理。在空域,一个2维的Gabor滤波器是一个正弦平面波和高斯核函数的乘积,具有在空间域和频率域同时取得最优局部化的特性,与人类生物视觉特性很相似,因此能够很好地描述对应于空间频率(尺度)、空间位置及方向选择性的局部结构信息。实际应用中,Gabor滤波器可以在频域的不同尺度,不同方向上提取相关特征。

2D-Gabor滤波器的公式为[12]

复数:

g(x,y:λ,θ,ψ,σ,γ)=

(5)

实部:

g(x,y:λ,θ,ψ,σ,γ)=

(6)

虚部:

g(x,y:λ,θ,ψ,σ,γ)=

(7)

其中:

x′=xcosθ+ysinθ,y′=-xsinθ+ycosθ

式中的λ为正弦函数的波长,θ为Gabor核函数的方向,ψ为相位偏移,σ是高斯函数的标准差。

图2为Gabor的一个核函数和其滤波结果。

图2　Gabor核函数和滤波结果

3.2基于多维特征的高斯混合模型

高斯混合模型(Gaussian Mixture Model,GMM)是逼近图像灰度直方图的一种概率模型,也是单一高斯概率密度函数的延伸。在对于灰度图像统计特性的描述中,高斯混合模型是被认为在描述区域内灰度缓慢变换的理想模型之一[13]。

设x={x1,x2,…,xn}是n个d维空间的训练样本值,并且假设各个样本之间是相互独立的,它们服从k类的高斯混合分布,它们加权的概率密度函数可表示为

(8)

其中

Nj(X;μj,σj)=

(9)

表示第j个高斯模型的概率密度函数。

令φj=(aj,μj,σj)为k个高斯模型的估计参数,本文通过背景、前景样本采用k-means聚类法[14]来计算这些参数。最后,仍利用贝叶斯公式获得它们的后验概率。

4实验分析

本文的实验数据来源于MICCAI(Medical Image Computing and Computer Assisted Intervention)2012年10月举办的右心室分割挑战项目,包括16个病人的心脏图像,数据是在1.5T磁场强度下,西门子仪器上采集的,数据采集相关参数:TR=50ms;TE=1.7ms;翻转角=;切片厚度7mm;矩阵大小=256×216;视场(FOV)=360mm×420mm;空间分辨率为0.75mm/pixel。

在实验过程中,为了实验结果的稳定性,我们人工地选定了每幅心脏图像的右心室区域中的一部分作为前景样本,背景则选取心室以外的其它区域。本文采用五个尺度,八个方向的Gabor滤波器对图像进行处理。由于Gabor滤波的结果图像维数过大,在使用混合高斯模型计算后验概率时容易出现奇异矩阵。采用加权平均将滤波的特征图降维到5维,并与原图像组成特征图像作为实验的输入图像。

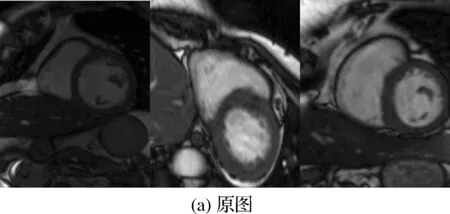
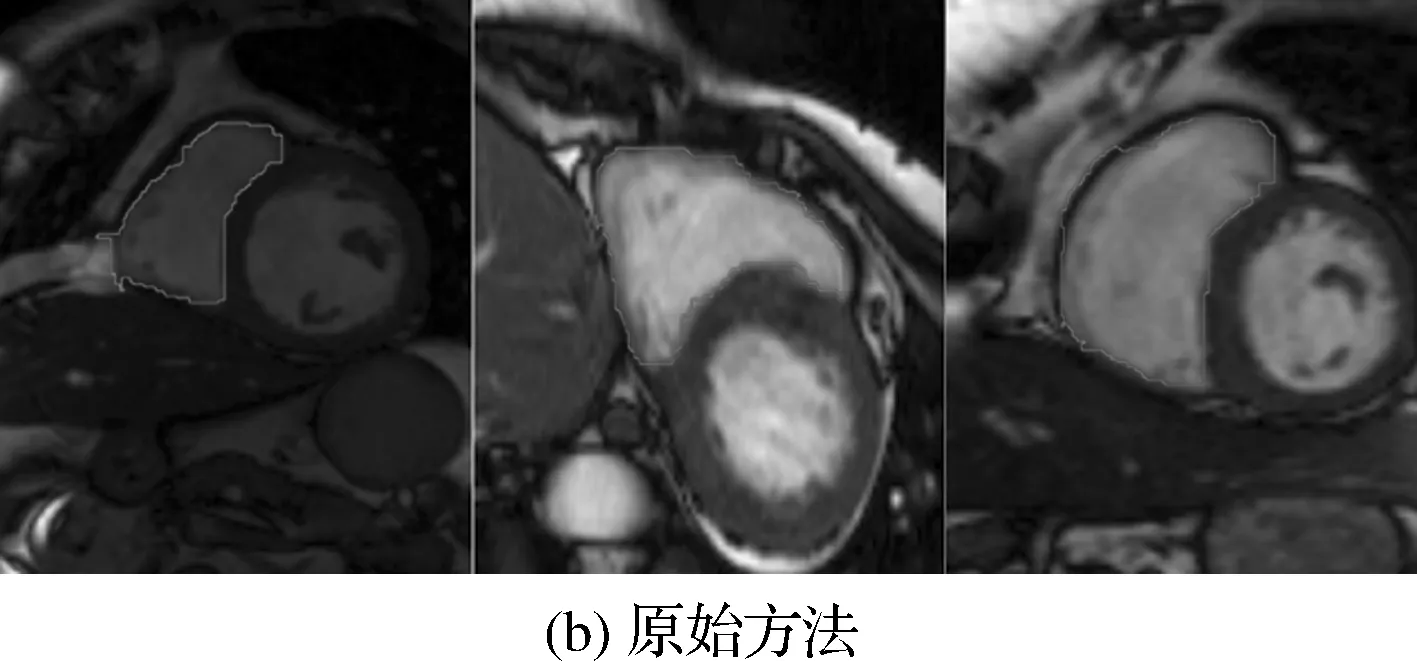
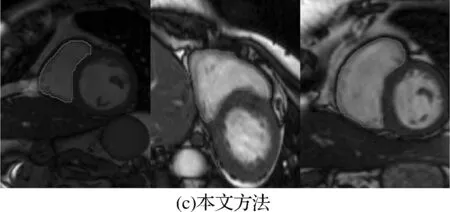
图3　实验结果的对比

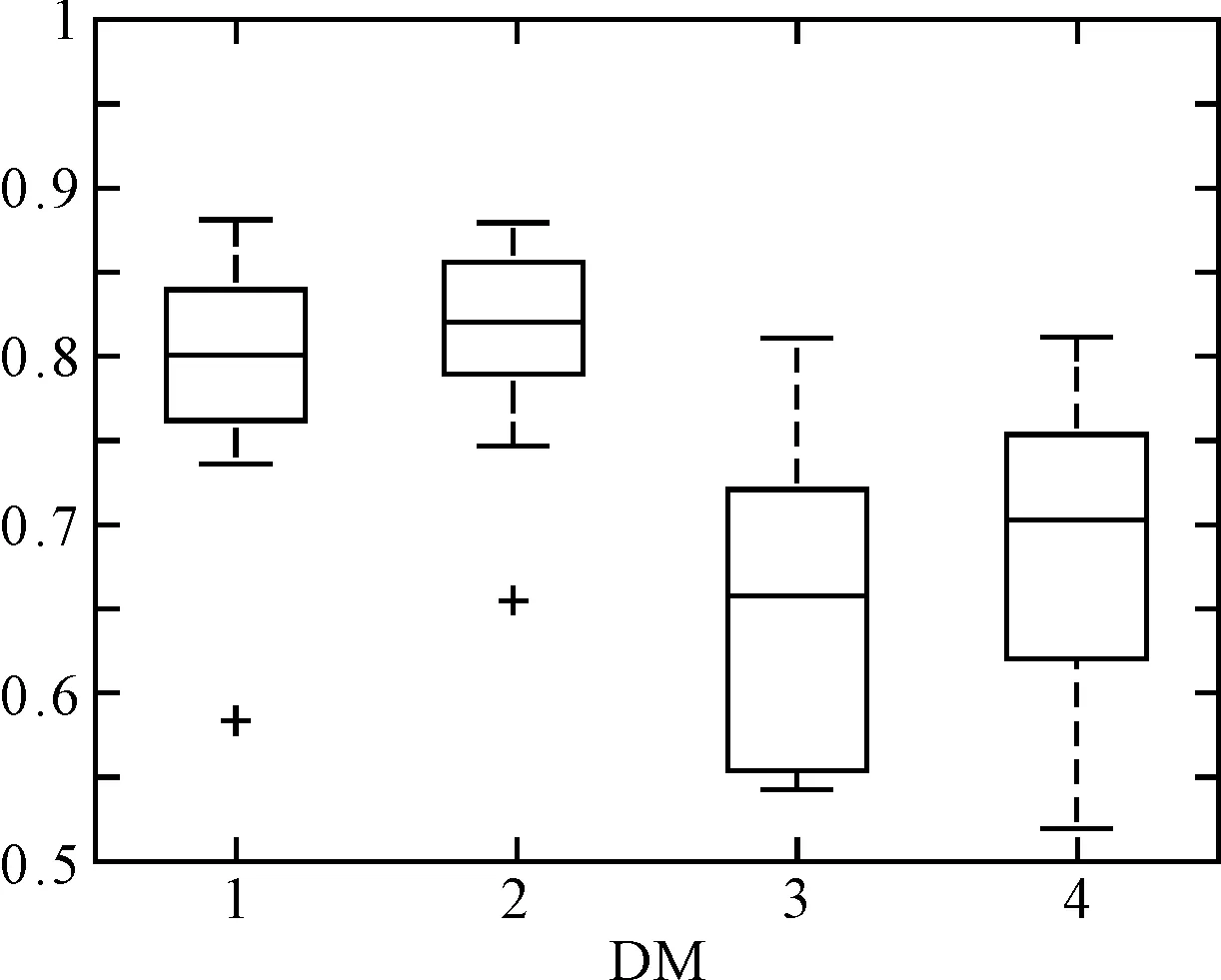
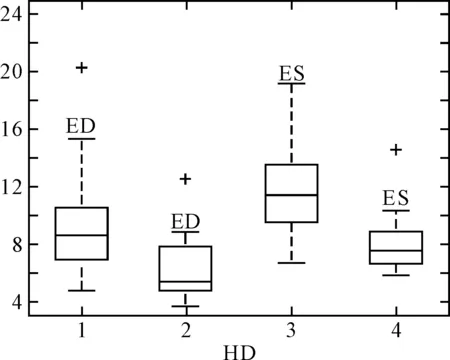
图4　DM和HD的箱线图

对16个病人240幅图像的分割结果与人工分割的金标准进行对比,得到了右心室内膜分割结果的DM(overlap Dice metric)和HD(Hausdorffdistance)的值,其中DM表示区域重叠率,值的范围从0(完全不匹配)到1(完全匹配),而HD是匹配点特征的一种方法,计算两个点集之间的相似度(最大距离)。原始方法得到的DM均值(±标准差)为0.7244(±0.21),本文的方法为0.7655(±0.18),原始方法的HD均值(±标准差)为10.67(±6.26),本文方法为7.07(±4.24)。图4为16组数据的箱线图,1,3为经典方法得到的舒张末期(ED)和收缩末期(ES)的数据,2,4则为本文方法的数据。

本文方法的DM中值在舒张末期和收缩末期分别为0.8082和0.7053,相比于经典方法的0.7891和0.6471,均有所提升。经典方法舒张末期和收缩末期HD的中值为8.635和11.415,本文方法则为5.395和7.565。结合图3和图4可以看出,本文的方法相比于经典算法,在准确率和稳定性上都有提升,同时边缘处理也比经典算法较为平滑。

5结语

由于心脏右心室具有高变异和壁薄等特点,造成其MR图像存在低对比度和边界模糊现象,采用传统Graph Cuts分割算法难以得到满意的效果。本文利用2D-Gabor滤波器,提取心脏MR图像边缘特征,借助高斯混合模型融入到Graph Cuts算法进行图像分割。相比较于经典方法,本文方法能取得更高的分割精度,一定程度上克服边界模糊的问题。在未来的研究工作中,将考虑引入更鲁棒和更优良的多维特征,实现更精准的分割,同时能使算法朝全自动化方向发展,提高工程实践性。

参 考 文 献

[1] Matthews JC, Dardas TF, Dorsch MP, et al. Right sided heart failure: diagnosis and treatment strategies[J]. Curr. Treat. Options Cardiovasc,2008,10(4):329-341.

[2] ElBaz MS, Fahmy AS. Active shape model with inter-profile modeling paradigm for cardiac right ventricle segmentation[J]. MICCAI,2012:691-698.

[3] Mahapatra D. Cardiac LV and RV segmentation using mutual context information[J]. MICCAI-MLMI,2012:201-208.

[4] 刘复昌,朱近.基于图划分的形状统计主动轮廓模型心脏MR图像分割[J].模式识别与人工智能,22(2):275-281.

LIU Fuchang, ZHU Jin. Graph Cuts and Shape Statistics Based Cardiac MR Image Segmentation Using Active Contours Model[J]. Pattem Recognition and Artificial Intelligence,22(2):275-281.

[5] Zuluaga MA, Cardoso MJ, Ourselin S. Multiatlas fusion: Automatic right ventricle segmentation using multi-label fusion in cardiac mri[C]//RV Segmentation Challenge in Cardiac MRI(MICCI),2012:403-411.

[6] Nambakhsh CMS, Rajchl M, Yuan J, et al. Rapid automated 3d rv endocardiumsegmentation in mri via convex relaxation and distribution matching[C]//RV SegmentationChallenge in Cardiac MRI(MICCI),2012:178-186.

[7] Grosgeorge D Petitjean C, Ruan S, Caudron J, et al. Right ventricle segmentation by graph cutwith shape prior[J]. Canadian Institute of Food Science & Technology Journal,2012,22(4):407-415.

[8] Maier O, Jimenez-Carretero D, SantosA, et al. Right-ventricle segmentation with 4d region-merging graph cuts in mr[C]//RV Segmentation Challenge in Cardiac MRI(MICCI),2012:315-323.

[9] Boykov Y, Veksler O. Fast approximate energy minimization via graph cuts[J]. IEEE Trans. Pattern Anal. Mach. Intell,2001,23:1222-1239.

[10] Yuri Boykov, Vladimir Kolmogorov. An Experimental Comparison of Min-Cut/Max-Flow Algorithms for Energy Minimization in Vision[C]//IEEE Transactions on PAMI,2004,26(9):1124-1137.

[11] Yuri Boykov, Marie-Pierre Jolly. Interactive Graph Cutsfor Optimal Boundary & Region Segmentation of Objects in N-D Images[J]. IEEE International Conference on Computer Vision,2001,1:105-112.

[12] Jesper Juul Henriksen. 3D surface tracking and approximation using Gabor filters[J]. South Denmark University,2007,March 28:21-55.

[13] Liu Yang, Huang Qinming, Gao Wen, et al. Playfield detection using adaptive GMM and its application in sports video analysis[J]. Journal of Computer Research and Development,2006,43(7):1270-1215.

[14] Drineas P, Vempala S, Vinay V, et al. Clustering Large Graphs via the Singular Value Decomposition[J]. Machine Learning(Kluwer Academic Publishers Hingham, MA, USA),56(1-3):9-33.

Segmentation of Right Ventricle MR Image Based on Gabor Filter and Graph Cuts

MA ShuangLU Xuesong

(Biomedical Engineering College, South-Central University for Nationalities, Wuhan430074)

AbstractRight ventricle segmentation is more and more important in clinical medical diagnosis and quantitative analysis of the diseasein medical image processing. Because the right ventricle of the cardiac MR images with high variability, thin wall, the border is not obvious characteristics, 2D-Gabor filter cardiac MRimagesand is used to get feature images, using Gaussian mixture model into Graph cuts algorithm, segmentright ventricle MR image. Compared to the original algorithm, the method has good effect on the stability and accuracy.

Key Words2D-Gabor, Graph cuts, right ventricle segmentation

收稿日期:2015年12月25日,修回日期:2016年1月30日

作者简介:马双,男,硕士研究生,研究方向:医学图像处理。陆雪松,男,博士,副教授,研究方向:医学图像的配准与信息融合、图像引导手术和生物医学图像分析。

中图分类号TP391.4

DOI:10.3969/j.issn.1672-9722.2016.06.039