矢量填充和插值算法的图像放大

(昆明理工大学信息工程与自动化学院　昆明　650500)

矢量填充和插值算法的图像放大

(昆明理工大学信息工程与自动化学院昆明650500)

摘要论文针对图像放大问题,建立了矢量化填充放大模型。并针对矢量化填充放大模型不能处理复杂图像的缺点,使用并比较了最邻近插值法、双线性插值法、双三次插值法三种不同的算法。并综合以上四个模型,得到以下结论:矢量化填充放大模型适用于较简单的可矢量化的图像,可无限放大,且不影响其成像。基于插值算法的三个模型中,最邻近法模型算法简单、计算量小、处理速度快,但处理后的图像会出现块效应,造成图像模糊。双线性插值法模型克服了最邻近法处理图像出现块效应的问题,其计算相比双三次法简单,但边缘细微结构会受到影响,产生轮廓模糊的现象。双三次插值法模型解决了以上两种算法的缺点,计算精度高,带有边缘增强的效果,能够较好保持图像的细微结构,但计算量较大。

关键词矢量填充; 最邻近插值法; 双线性插值法; 双三次插值法

Class NumberTP309.7

1引言

位图在放大时,图像质量常会有所下降,如容易产生较为明显的模糊或马赛克等现象。现在待解决的是如何建立合理的数学模型,来设计一个放大位图的算法,使图像在被放大后仍能尽量保持较好的图像质量。本文为大家呈现几种解决该问题的方法[1]。

同时针对位图放大时容易产生较为明显的模糊或马赛克等现象。通过矢量图的特性可知,作为矢量图,在放大的时候能保持一定图像比例。但是此类方法产生的矢量图大多是一些构图简单、可矢量化的、颜色较为单一的位图。目前,为得到复杂图像的放大清晰位图,多采用插值算法对位图进行处理。常用的插值算法有最邻近插值法、双线性插值法、双三次插值法等,不同插值算法对图像的处理效果不一样。本文采用最邻近插值法、双线性插值法、双三次插值法三种算法对放大图像进行放大、比较[2]。

2矢量化填充放大模型

对原图进行位图矢量化之前直接对整个图像的特征点进行拟合的求解方法,由于数据过少,会造成函数的波动,使得图像不够圆滑,因此采用分块方式对图像进行分块,具体求解过程如下:

1) 将图像分为四个部分

采用分块方式将二值化后的图像分为四块区域,划分区域如图1所示。

一二三四

图1划分区域图

针对区域划分,利用Matlab求解的程序如下:

[mm,nn]=size(A)

B1=A(1:mm/2,1:nn/2);

B2=A(1:mm/2,nn/2+1:nn);

B3=A(mm/2+1:mm,1:nn/2);

B4=A(mm/2+1:mm,nn/2+1:nn);

2) 针对区域一

对图像边缘轮廓的提取有许多的研究和方法,常用的图像的边缘提取的梯度算子有Roberts算子、Sobel算子、Canny算子、Prewitt算子和Laplace算子,本文最终采用Canny算子[3～4]。

对第一部分图像进行预处理以后,利用canny算子对其进行边缘检测,检测结果如图2所示。

图2　提取图像的边缘

特征点的提取是位图矢量化过程中重要的一步,该步骤主要是从检测出的边缘中提取出表示图像轮廓关键特征的点[5]。本模型采用的Harris算法是稳定性和准确度都较高的基于灰度的角点检测算法。

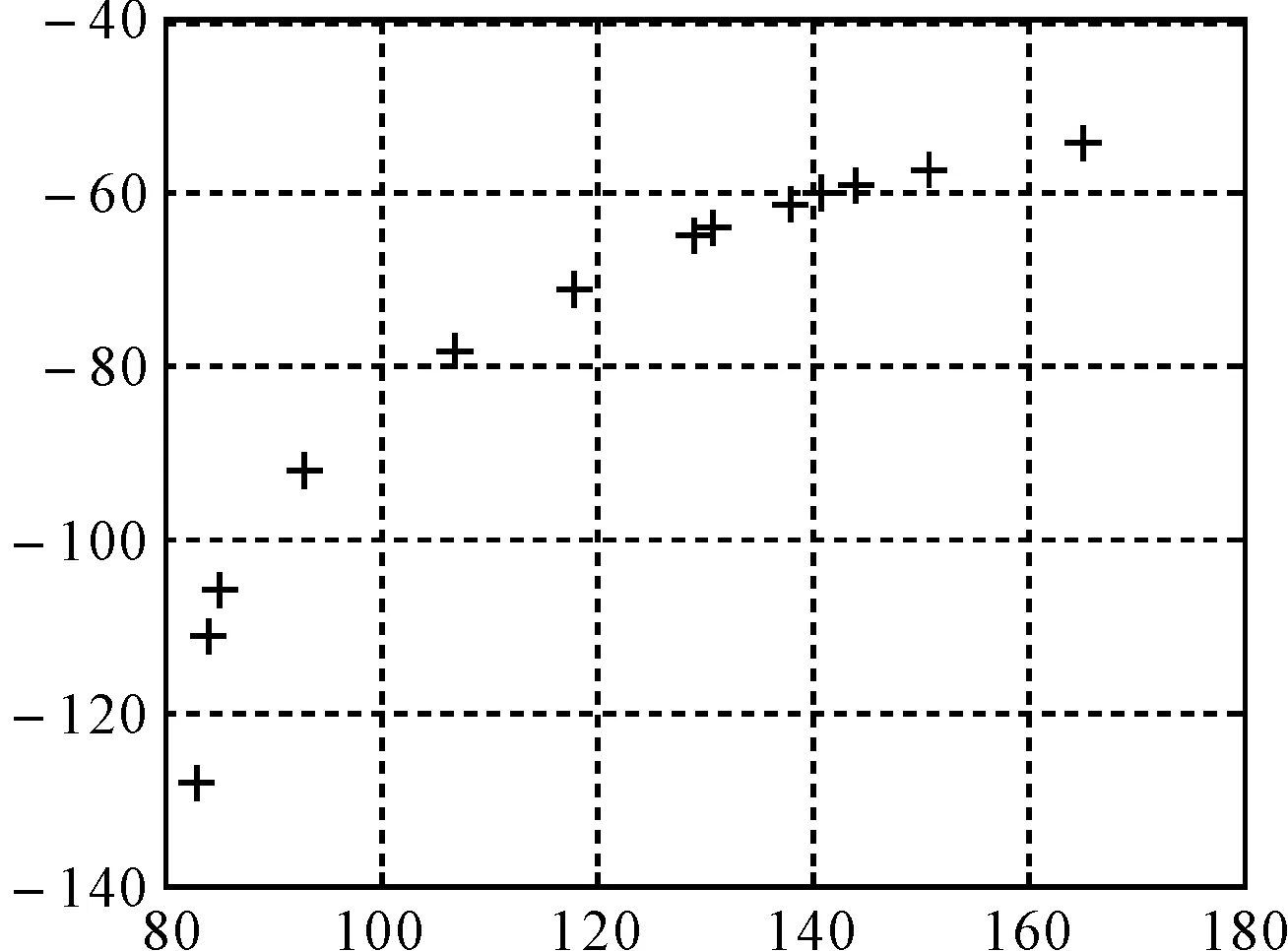
图3　特征点提取结果

曲线拟合是指用连续曲线近似地刻画或比拟平面上离散点组所表示的坐标构造之间的函数关系[6～7]。

Matlab求解程序[8]如下:

if strcmp(flag,'paint')

xx=min(x):0.1:max(x);

yy=polyval(p,xx);

plot(xx,-yy,'g');

hold on

end

此时对拟合函数进行归类,并标记取值范围,Matlab求解程序如下:

[m,n]=size(ans_max);

disp('拟合后函数');

for i=1:n

fprintf ('x取值范围[%d,%d] ',

ans_min(i),ans_max(i))

fprintf ('第%d段:y= ',i);

disp(ploy(i));

end

对其他三个区域采用相同的处理方法,将得到的四块图像照分割次序还原,得到原图曲线。

3矢量图放大填充

1) 模型背景知识

矢量图根据几何特性来绘制图像,矢量可以是一个点或一条线,矢量图只能靠软件生成,文件占用内在空间较小,因为这种类型的图像文件包含独立的分离图像,可以自由无限制地重新组合。它的特点是放大后图像不会失真,和分辨率无关,文件占用空间较小,适用于图像设计、文字设计和一些标志设计、版式设计等。

2) 模型的建立与求解

设此时拟合完毕后的函数自变量为X,因变量为Y。为了放大矢量图,可先对定义域X的值进行扩充,采用式(1):

X′=[Xmin*K,Xmax*K]

(1)

为了得到特定的X值M,需将扩充后的定义域X′进行式(2)计算:

M=X′/K

(2)

得到特定的X值后,可将它代入拟合完毕后的函数f(x),计算出特定的Y值,求出值域。此时便可对值域的值进行扩充,采用式(3):

Y′=[Ymin*K,Ymax*K]

(3)

最后将扩充后的定义域和值域进行曲线拟合,得到的函数f′(x)便为放大后的矢量图。

由于有灰度图,因此为了简化计算,可以不对矢量图进行填充。

对于此问题,采用Matlab求解:

Magnification=8;%扩大倍数

for i=1:n

fprintf ('x取值范围[%d,%d] ',

ans_min(i)*Magnification,

ans_max(i)*Magnification)

fprintf ('第%d段:temp= ',i);

disp(ploy(i));

fprintf ('y=%d*temp ',

Magnification);

End

4最邻近插值算法模型

最邻近插值是最简单的插值算法[9],也叫零阶插值,最邻近插值的核心思想是首先将(x,y)经空间变换映射为(x′,y′),如果(x′,y′)是非整数坐标,则寻找(x′,y′)的最近邻,并将最近邻的灰度值赋给校正图像(x,y)处的像素。

该算法原理简单,即每一个待插值点的像素值取在原图像中相应点周围四个相邻点中欧氏距离最短的一个。该算法计算量小,但其缺点是可能会有块效应,造成图像模糊,放大后图像质量不高。最邻近插值公式如式(4)所示:

f(x+u,y+v)=f(x,y)

(4)

其中f(x,y)表示原图像在(x,y)位置处像素点的像素值;u,v均为[0,1)区间的浮点数,分别表示待插值点与最邻近像素点在水平和竖直方向的距离,x和y的取值范围大于等于0。

简言之,最邻近插值输出的像素灰度值就等于距离它映射到的位置最近的输入像素的灰度值。该算法简单,在许多情况下都能得到令人满意的结果,但是当图像中存在像素之间灰度级有变化的细微结构时,该算法会在图像中产生人为加工的痕迹。

在Matlab中编程实现用最邻近插值算法实现图像的放大,文中选择大小为128*128的图像进行实验。

本文中随机选择图4做为目标图像。

图4　目标图像

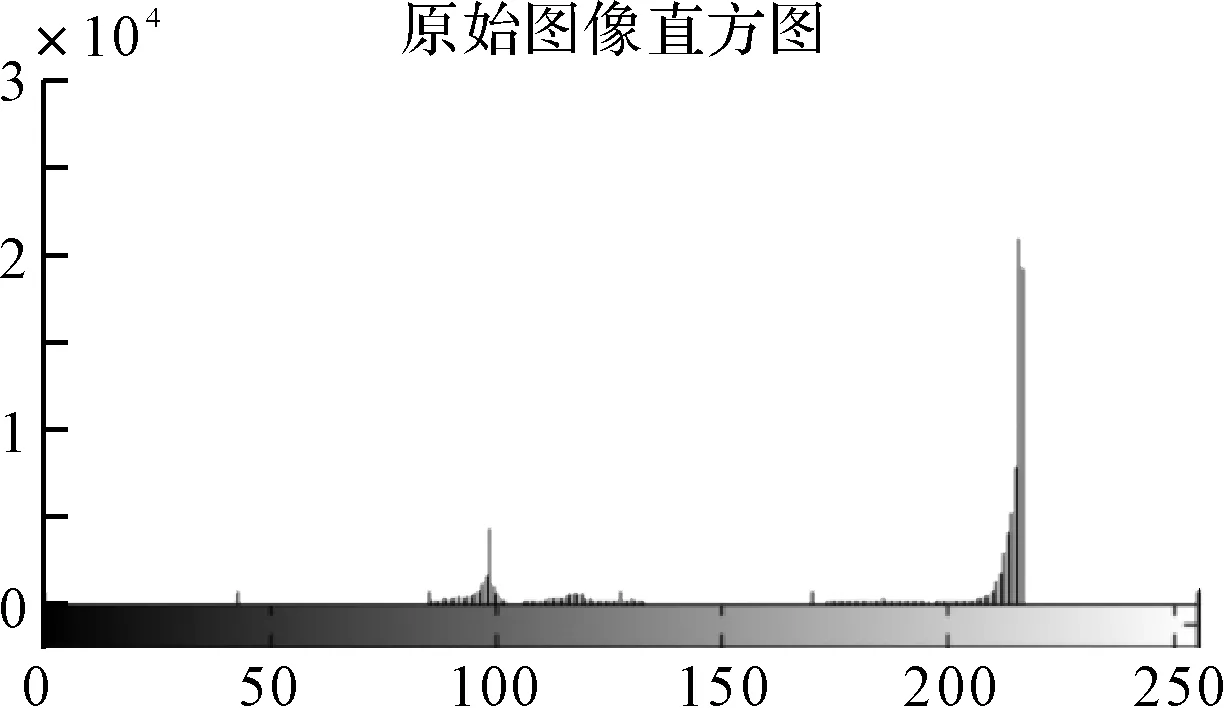
图5　原始图像直方图

采用最邻近插值法对目标图像放大处理,效果如图6所示。

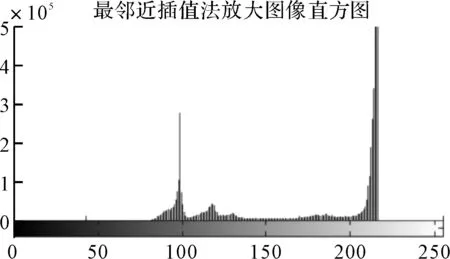
图6　最邻近插值法放大图像直方图

对比直方图可看出,用最邻近插值法放大的图像在给定Level值下像素的数量有明显的增加,即实现了图像的放大。实现代码如下:

A = imread('./test1.jpg');%读取图像信息

imshow(A); %显示原图

title('原图128*128');

Row = size(A,1); Col = size(A,2);%图像行数和列数

nn=8;%放大倍数m = round(nn*Row);%求出变换后的坐标的最大值

n = round(nn*Col);

B = zeros(m,n,3);%定义变换后的图像

for i = 1 : m

for j = 1 : n

x = round(i/nn); y = round(j/nn);

%最小临近法对图像进行插值

if x==0 x = 1; end

if y==0 y = 1; end

if x>Row x = Row; end

if y>Col y = Col;end

B(i,j,:) = A(x,y,:);

end

end

B = uint8(B);%将矩阵转换成8位无符号整数

figure; imshow(B);

title('最邻近插值法放大8倍1024*1024');

5双线性插值算法模型

双线性插值[10],又称为双线性内插,在数学上,双线性插值是有两个变量的插值函数的线性插值扩展,其主要思想是在水平和竖直方向上分别进行一次线性插值。

其基本原理为:对于一个目的像素,通过坐标的反向设置变换得到浮点的坐标(x+u,y+v),其中x和y均为大于等于零的整数,u和v为[0,1)区间的浮点数,则这个像素的值可由原图像中坐标为(x,y),(x+1,y),(x,y+1),(x+1,y+1)所对应的相邻四个像素的值决定,即如式(5)所示:

f(x+u,y+v)=(1-u)(1-v)f(x,y)

+(1-u)vf(x,y+1)

+u(1-u)f(x+1,y)

+uvf(x+1,y+1)

(5)

其中f(x,y)表示源图像(x,y)处的像素值。

图7　双线性内插值原理

采用双线性内插值法对目标图像进行放大处理,效果如图8所示。

与最邻近插值算法相比,双线性插值缩放后图像质量更高,不会出现像素值不连续的情况。但是双线性插值算法计算量比最邻近插值大,且有低通滤波器的性质,所以会使高频分量受损,导致图片边缘发生细微结构变化。

实现代码如下:

C=imresize(A,8,'bilinear'); %双线性插值

figure; imshow(C);

title('双线性内插值法放大8倍1024*1024');

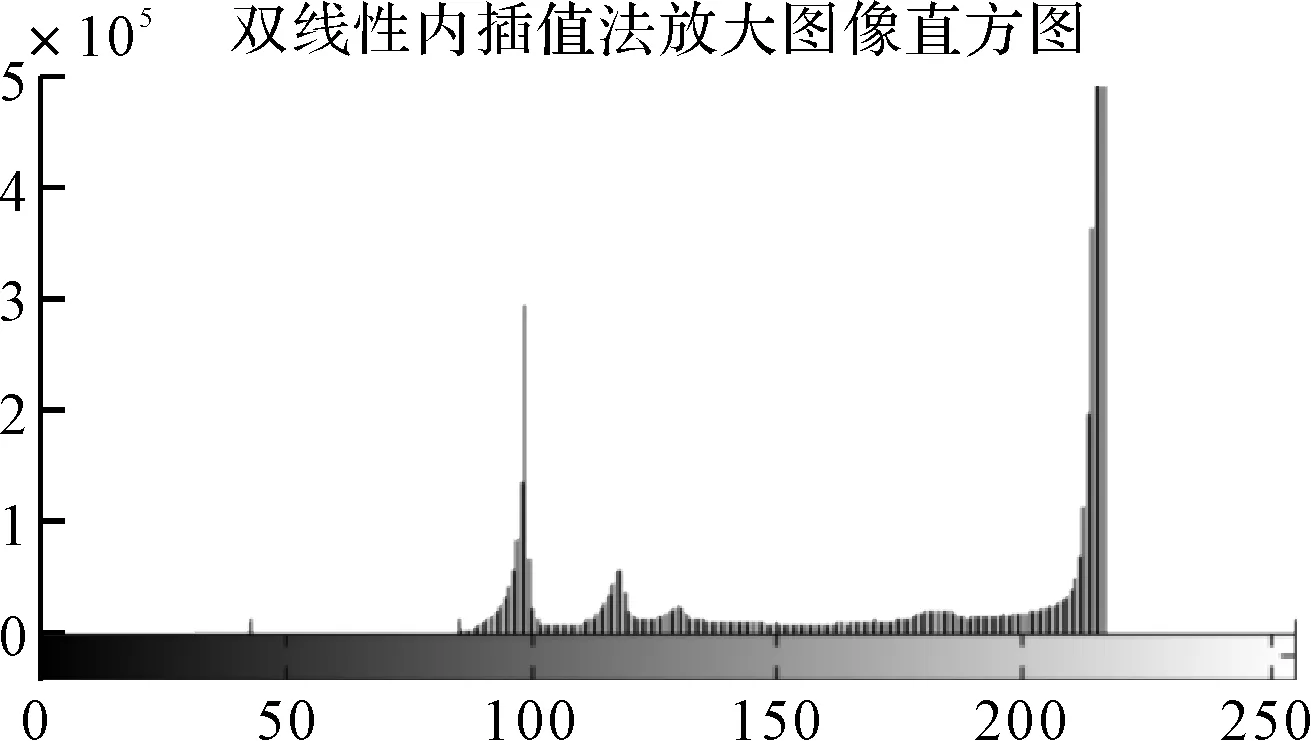
图8　双线性内插值法放大图像直方图

6双三次插值算法模型

双三次插值又称立方卷积插值,双三次插值算法根据目的像素点周围的16个像素点的灰度值作三次线性插值,此算法不仅考虑到像素点周围4个直接相邻灰度影响,而且还考虑到各邻点间灰度值变化率的影响,图像经过三次运算可以得到高分辨率图像放大的结果。该算法需要选取插值基函数来拟合数据,其最常用的插值基函数如图9所示。

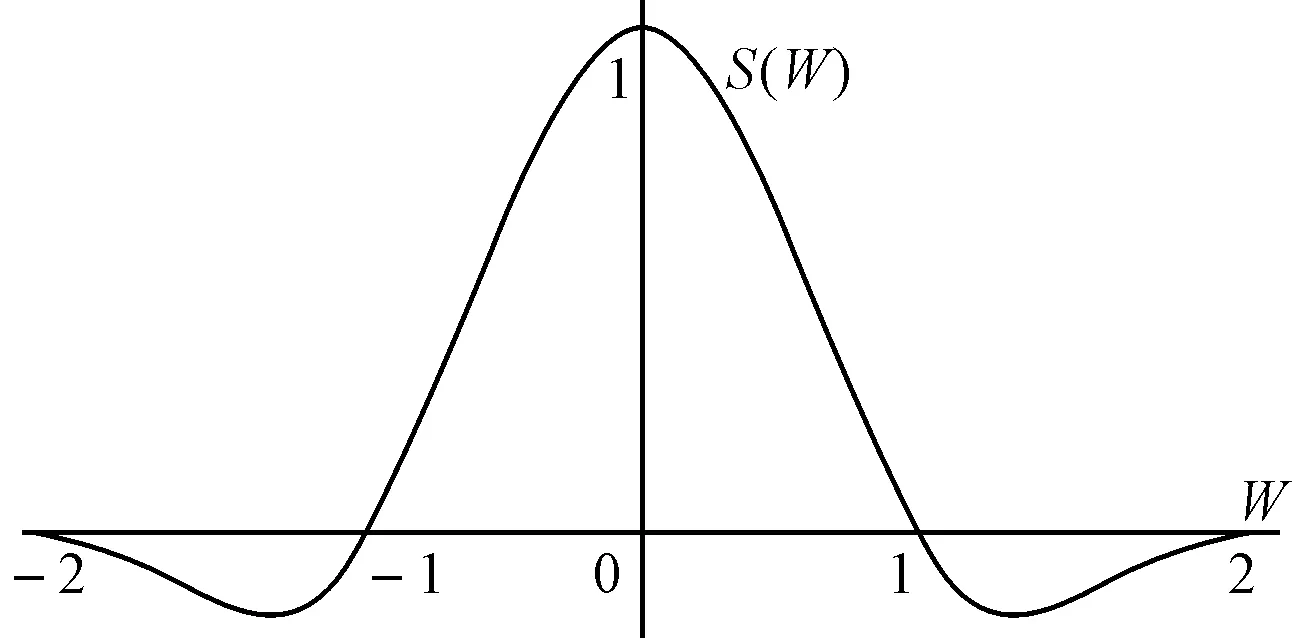
图9　双三次内插基函数

其数学表达式如下:

(6)

双三次插值的一般公式由二元双三次插值公式推导而来,其共有(3+1)2=16个系数,其公式表示如式(7)所示:

z=a1+a2x+a3y+a4x2+a5xy+a6y2+a7x3

+a8x2y+a9xy2+a10y3+a11x3y+a12xy3

+a13x2y2+a14x3y2+a15x2y3+a16x3y3

(7)

该方法考虑一个浮点坐标(x+u,y+v)周围的16个邻点,目标像素值f(x+u,y+v)可由如下插值公式得到:

f(x+u,y+v)=[A]*[B]*[C]

(8)

[A]=[S(u+1)S(u+0)S(u-1)S(u-2)]

(9)

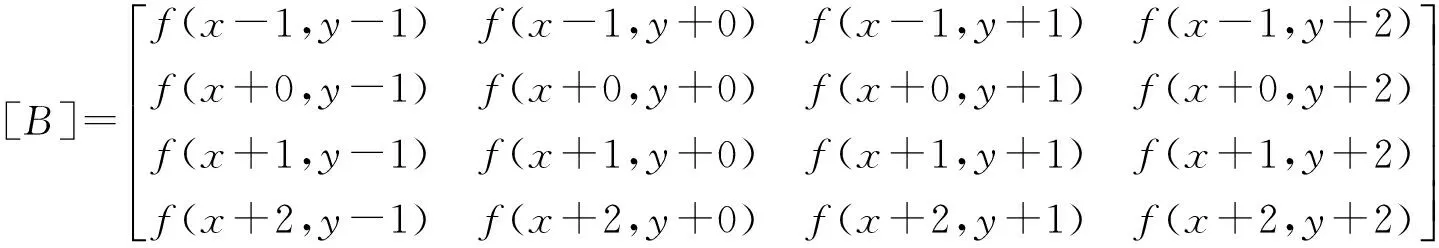
(10)

------------------------------

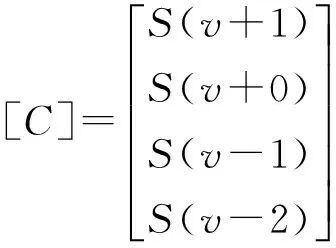
(11)

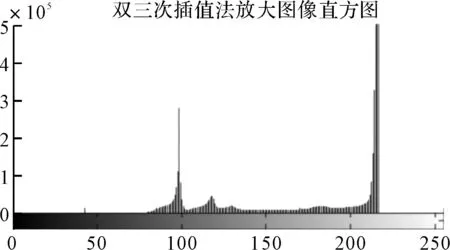
图10　双三次插值法放大图像直方图

双三次插值能得到高分辨率图像放大的结果,但比最邻近插值和双线性插值更加复杂,这样也就同时导致了计算量的剧增。

实现代码如下:

D=imresize(A,8,'bicubic');

%双三次插值放大8倍

figure;

imshow(D);

title('三次卷积法放大8倍1024*1024');

7结语

本文针对清晰化放大图像,建立了四个模型。第一个模型基于图像矢量化,对矢量图进行填充放大。该算法虽然只能处理简单的可矢量化的图像,但是可放大倍数非常可观,并且经该算法放大的图像的清晰度是所有模型中最优的。所以,该模型比较适用于对相对简单的图像的放大处理。

最邻近插值算法模型、双线性插值算法模型、双三次插值算法模型都是采用对位图直接插值的算法,其基本原理一样,都是一个图像数据再生的过程——它由原始具有较低分辨率的图像数据再生出具有更高分辨率的图像数据。但获得插值点像素的具体计算方法存在较大差异,最邻近插值算法取的值是距离原点映射到的位置最近的输入像素的灰度值;双线性插值算法的思想是在水平和竖直方向上分别进行一次线性插值;双三次插值算法根据目的像素点周围的十六个像素点的灰度值作三次线性插值。

三个模型都能对各种位图进行放大处理,但放大效果不一样,其中,双三次插值算法对图像的处理效果最好,双线性插值算法次之,最邻近插值算法的处理效果最差。

综上,本文中四个模型各有其优缺点,实际中根据具体情况采用适合的模型。

参 考 文 献

[1] 姜启源,谢金星,叶俊.数学建模[M].北京:高等教育出版社,2011:216-253.

JIANG Qiyuan, XIE Jinxing, YE Jun. Mathematical modeling[M]. Beijing: Higher Education Press,2011:216-253.

[2] 张海燕,吴方.几种插值算法的比较研究[J].计算机技术与发展,2012,22(2):234-237.

ZHANG Haiyan, WU Fang. Coparative Research of Interpolation Algorithms[J]. Computer Technolocy And Development,2012,22(2):234-237.

[3] Rafael C. Gonzalez, Richard E. Woods, Steven L. Eddins.数字图像处理[M].北京:电子工业出版社,2005:167-190.

Rafael C. Gonzalez, Richard E. Woods, Steven L. Eddins. digital image processing[M]. Beijing: Electronic Industry Press,2005:167-190.

[4] [美]赫恩.计算机图像学[M].第三版.北京:电子工业出版社,2010:58-97.

Hearn. Computer image[M]. Third edition. Beijing: Electronic Industry Press,2010:58-97.

[5] 刘玉兰,葛庆平.一种间接提取轮廓特征点的算法[J].计算机工程与应用,2004,40(10):51-52.

LIU Yulan, GE Qingping. An Algorithm of Selecting Feature Points Indirectly in an Outline[J]. Computer Engineering and Applications,2004,40(10):51-52.

[6] 胡魁贤,严宏志,朱自冰,等.截面轮廓曲线分段约束拟合[J].计算机工程与科学,2009,31(7):53-56.

HU Kuixian, YAN Hongzhi, ZHU Zibing, et al. Fitting Planar Curves with Restraint Method[J]. Computer Engineering and Science,2009,31(7):53-56.

[7] 刘玉兰,葛庆平.闭合数字曲线的多项式递归拟合[J].计算机工程与应用,2005,41(7):51-53.

LIU Yulan, GE Qingping. Recursive Fitting of Closing Digital Curve Using Polynomials[J]. Computer Engineering and Applications,2005,41(7):51-53.

[8] 仵峰.用Matlab进行图形矢量化[J].中国农村水利水电,2007,(8):31-33.

WU Feng. The Vector quantization By Matlab[J]. China Rural Water and Hydropower,2007,(8):31-33.

[9] 梁小利,孙洪淋.基于线性插值算法的图像缩放及实现[J].长沙通信职业技术学院学报,2008,7(2):49-51.

LIANG Xiaoli, SUN Honglin. Image zooming based on linear interpolation algorithm and its realization[J]. Journal of Changsha Telecommunications and Technology Vocational College,2008,7(2):49-51.

[10] 冯慧君,陶素娟,李隆.基于双线性插值算法的图像放缩技术与实现[J].计算机应用与软件,2004,21(7):117-119.

FENG Huijun, TAO Sujuan, LI Rong. Double Linear Inserting Algorithm Based Image Zooming And Its Realization With VC++[J]. Computer Applications and Software,2004,21(7):117-119.

Vector Filling and Interpolation Algorithms of Image Magnification

WU JunbinWU ShengWU Xingjiao

(School of Information Engineering and Automation, Kunming University of Science and Technology, Kunming650500)

AbstractIn view of the problem of image magnification, this paper establishes the vector filling amplification model. And fill the zoom model can’t deal with complex vector quantization for image shortcomings, using the adjacent interpolation method, bilinear interpolation method, double three interpolation method of three different algorithms are compared. And integrated the above four models, the following conclusion is gotten: fill amplification vector quantization model suitable for simple images, vector quantization can be unlimited amplifier, and does not affecting the imaging. Three models based on interpolation algorithm, the neighboring method model algorithm is simple, small amount of calculation, fast processing speed, but after processing the image will appear block effect, cause blurred images. Bilinear interpolation model overcame the neighboring method processing image block effect problem, compared the calculation method of double three simple, but the edge structure will be affected, produce the outline of the fuzzy phenomenon. Double three interpolation model to solve the disadvantages of the above two kinds of algorithm, the calculation accuracy is high, with the effect of edge enhancement, can better keep the image structure, but the large amount of calculation.

Key Wordsvector filling, adjacent interpolation method, bilinear interpolation method, double three interpolation method

收稿日期:2015年12月16日,修回日期:2016年1月24日

作者简介:吴俊斌,男,研究方向:算法设计、程序设计。吴晟,男,教授,硕士生导师,研究方向:信息安全,算法研究等。吴兴蛟,男,硕士研究生,研究方向:软件工程、算法设计、程序设计。

中图分类号TP309.7

DOI:10.3969/j.issn.1672-9722.2016.06.034

吴俊斌吴晟吴兴蛟