基于四元数极谐变换的鲁棒数字水印算法

张　博

(长沙师范学院电子与信息工程系　长沙　410100)

基于四元数极谐变换的鲁棒数字水印算法

张博

(长沙师范学院电子与信息工程系长沙410100)

摘要论文提出了一种基于四元数极谐变换的鲁棒数字图像水印算法。该算法结合四元数极谐变换的不变特性,对彩色图像载体进行四元数极谐变换,变换后,选取一部分稳定的四元数极谐变换矩的幅值,进而根据量化调制。选取嵌入水印信息前后的四元数进行重构得到两个重构图像,然后对这两个重构图像做差值运算,将得到的差值叠加到原载体图像中,继而得到含水印图像。仿真实验表明,基于四元数极谐变换的鲁棒数字水印算法能够很好地抵抗常规攻击和几何攻击,具有较好的鲁棒性。

关键词四元数极谐变换; 数字水印; 抗几何攻击; 鲁棒性

Class NumberTP309

1引言

数字水印是一种对图像真伪鉴别的主动认证。在版权保护的过程中,既要保证原始信息在听觉或视觉上不受到影响,还要当数据信息受到外界干扰或攻击时能够完全或部分提取出水印数据[1],从而达到版权保护的目的。

四元数属于复数的扩展,是一种超复数[2],即可看成四维的复数,它是由一个实部及三个虚部组成。由此,国内外一些学者利用四元数理论进行图像处理,得到了较好的结果。

Bas较早地将四元数傅里叶变换引入数字水印中,采用量化索引调制的方法将水印信息嵌入到彩色图像中[3];Ma等提出了一种基于四元数傅里叶变换的半盲算法,算法在目标图像中选取参考点,然后在这些参考点周围领域的频域系数中嵌入相应水印[4];Tsui等利用四元数元素的特征设计了视觉掩膜,然后将水印信息嵌入到四元数傅里叶变换中[5];Gao等利用四元数傅里叶-梅林变换将水印信息嵌入到彩色图像中,取得了较好的结果[6];江淑红等利用四元数傅里叶变换进行数字水印的嵌入和目标跟踪[7]。但是基于四元数的数字水印算法在国内的研究刚刚开始,并且大部分算法都是基于四元数的傅里叶变换。本文结合四元数极谐变换的不变特性,对彩色图像载体进行四元数极谐变换,基于四元数极谐变换的鲁棒数字水印算法能够很好地抵抗常规攻击和几何攻击,具有较好的鲁棒性。

2彩色图像的四元数极谐变换

2.1彩色图像的四元数描述

Hamilton是英国著名的数学家,1843年,他正式给出四元数理论[8],四元数属于复数的扩展,是一种超复数[2],即可看成四维的复数,它是由一个实部及三个虚部组成,其表达式可描述如下

q=a+bi+cj+dk

(1)

其中,a,b,c,d均为实数,i,j,k为虚数单位,并且它们之间满足一定的规则,具体规则如下

i2+j2+k2=-1

ij=-ji=k,jk=-kj=i,ki=-ik=j

(2)

相对地,四元数的共轭和幅值表示如下

(3)

假定一个彩色图像的大小为M×N,图像中的某一个像素用f(x,y)来表示,其中,x和y分别为像素所在矩阵的行和列的位置,并且x∈[1,M],y∈[1,N]。彩色图像是由红色通道、绿色通道和蓝色通道三个通道组成,此时,将这三个通道分别对应成四元数的三个虚部,令其实部为0,这样,在颜色空间的彩色图像就可以用来描述四元数,并且作为了一个整体矢量,即表示成为一个无实部的纯虚四元数,表达式如下

f(x,y)=fR(x,y)i+fG(x,y)j+fB(x,y)k

(4)

其中,fR(x,y)、fG(x,y)和fB(x,y)分别表示图像的红、绿和蓝三色通道,i、j和k为虚数单位。

与传统的利用单色通道或提取亮度图像后处理彩色图像的方法相比较,基于四元数的彩色图像处理方法更加能够体现其图像信息的完整性,能够更好地将其图像颜色信息保存下来。

2.2彩色图像的四元数极谐变换

结合灰度图像的极坐标谐波变换(PHT)和四元数矩的定义[9～10],通过公式推导,可以得到彩色图像四元数PHT的定义,假设f(r,θ)为极坐标下的彩色图像,定义出如下形式的彩色图像四元数PHT:

(5)

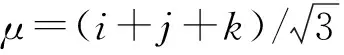
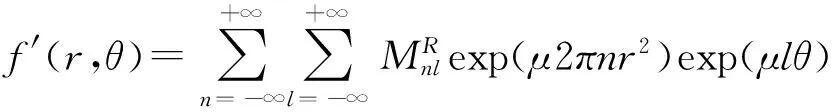
(6)

3四元数极谐变换的不变特性分析

3.1四元数极谐变换的旋转不变性

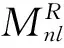
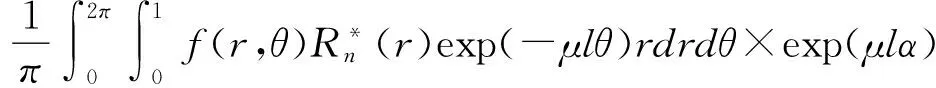
(7)

对上面等式进行两端取模操作,即为

(8)

由此可知,原始彩色图像旋转α角度后的四元数极谐变换的幅值与原彩色图像四元数极谐变换的幅值是相等的,即彩色图像四元数极谐变换的幅值具有旋转不变特性。

3.2四元数极谐变换的缩放不变性

在极坐标系下,将彩色图像归一化到单位圆内,再计算该彩色图像四元数极谐变换,此时所计算得到的彩色图像四元数极谐变换具有缩放不变性。对于给定的彩色图像函数g(r′,θ),找到其半径k,则有r′的变化范围为0≤r′≤k,其归一化彩色图像函数可表示为

f(r,θ)=g(kr,θ)=g(r′,θ)

(9)

其中,r=r′/k的变化范围为0≤r≤1,f(r,θ)为归一化后的彩色图像函数。由于同一彩色图像函数f(r,θ),0≤r≤1经过缩放而得到的任一彩色图像f(r′/k,θ),按照上面公式最终都可以归一化为同一个彩色图像函数f(r,θ),所以归一化后的彩色图像四元数极谐变换就具有了缩放不变性。

3.3四元数极谐变换的平移不变性

四元数极谐变换的平移不变性是通过几何矩来实现的。对于任意一幅彩色图像,可以先计算其质心,待获得彩色图像的质心坐标后,便可以将彩色图像中心移到彩色图像的质心坐标,再进行计算彩色图像的四元数极谐变换,此时计算得到的彩色图像四元数极谐变换就具有了平移不变性,而彩色图像的质心坐标(xc,yc)可以通过零阶几何矩和一阶几何矩得到,即为

xc=(m1,0(fR)+m1,0(fG)+m1,0(fB))/m0,0

yc=(m0,1(fR)+m0,1(fG)+m0,1(fB))/m0,0

m0,0=m0,0(fR)+m0,0(fG)+m0,0(fB)

(10)

其中,m0,0(fR)、m1,0(fR)和m0,1(fR)表示R颜色分量的零阶和一阶几何矩,m0,0(fG)、m1,0(fG)和m0,1(fG)表示G颜色分量的零阶和一阶几何矩,m0,0(fB)、m1,0(fB)和m0,1(fB)表示B颜色分量的零阶和一阶几何矩。

4基于四元数极谐变换的数字水印算法

4.1四元数极谐变换矩的选取

载体图像I(x,y)是尺寸为M*M的彩色图像,水印图像w(i,j)是尺寸为P*P的二值图像,先将水印图像转换成一维水印图像W={wi,i=1,…,L},其中,L=P*P,wi∈{0,1}。

1) 对载体图像I(x,y)求四元数PHT,对于数字水印嵌入而言,只有计算精确的四元数PHT矩才能够被用于水印信息的嵌入。Xin[11]等指出ZMs/PZMs在不同的重复度下计算得到的矩值精确性并不相同。在实验中,发现彩色图像四元数PHT同样满足这样的特性。利用一幅恒定像素值C的彩色图像,令其恒定像素值为f(r,θ)=C。根据其四元数PHT定义,能够得到四元数PCET结果为

(11)

在实验中,发现计算所得到的四元数PHT,当l=4m,m∈Z时,并不是总是满足上面的结论,为了说明这一点,任意选取两幅大小为128×128×3,恒定像素值分别为60和168的彩色图像为例,计算其四元数PHT后,其一部分四元数PCET(极坐标复指数变换)矩的幅值见表1、表2所示。

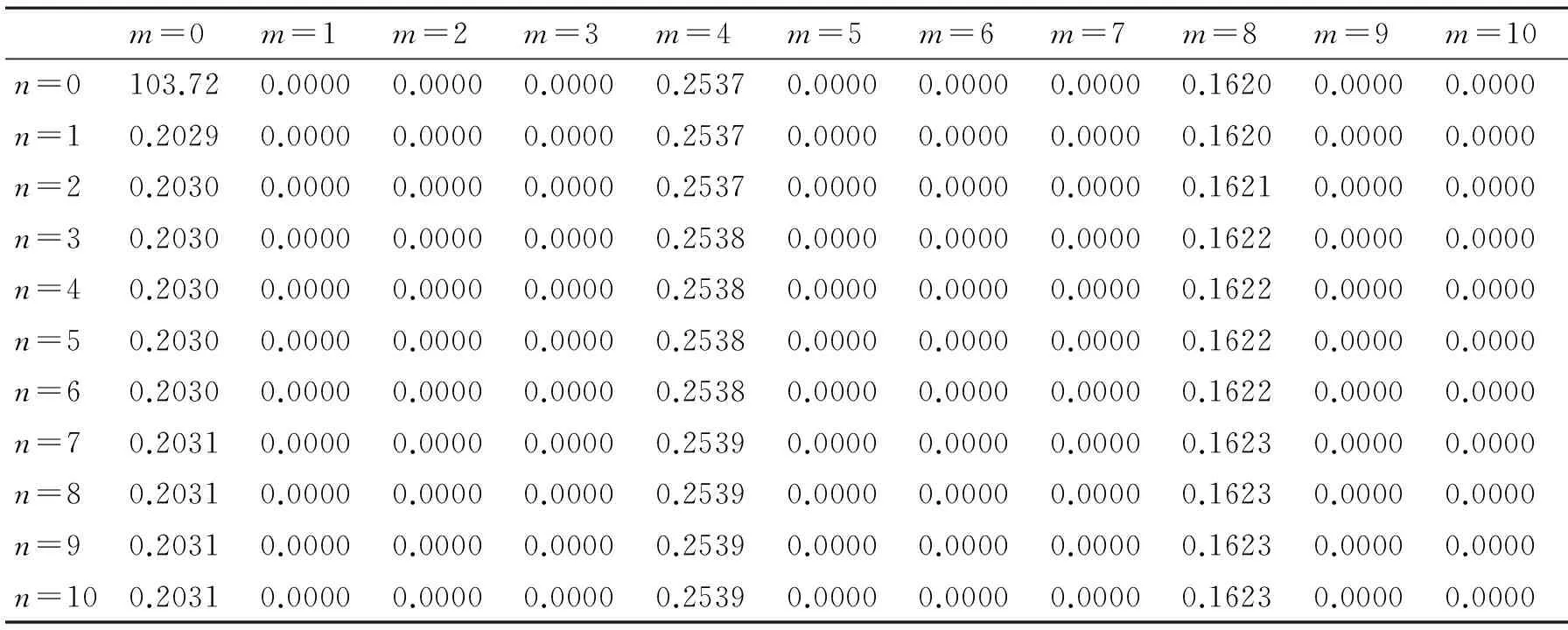
表1　恒定像素值60

从实验结果发现,当l=4m,m∈Z时,四元数PHT的幅值不为0,且偏差较大,这些幅值不符合式(11)的规律,这些计算不精确的四元数PHT矩不能用于数字水印信息的嵌入。最后,得到恒定像素下四元数PCET的矩幅值规律如下:

(12)

2) 对彩色载体图像求四元数PHT时,由于四元数PHT幅值不是关于中心对称的,但它们满足某种对应关系,所以选取四元数PHT用于水印嵌入时,只考虑在阶数大于或等于0的四元数PHT中选取。

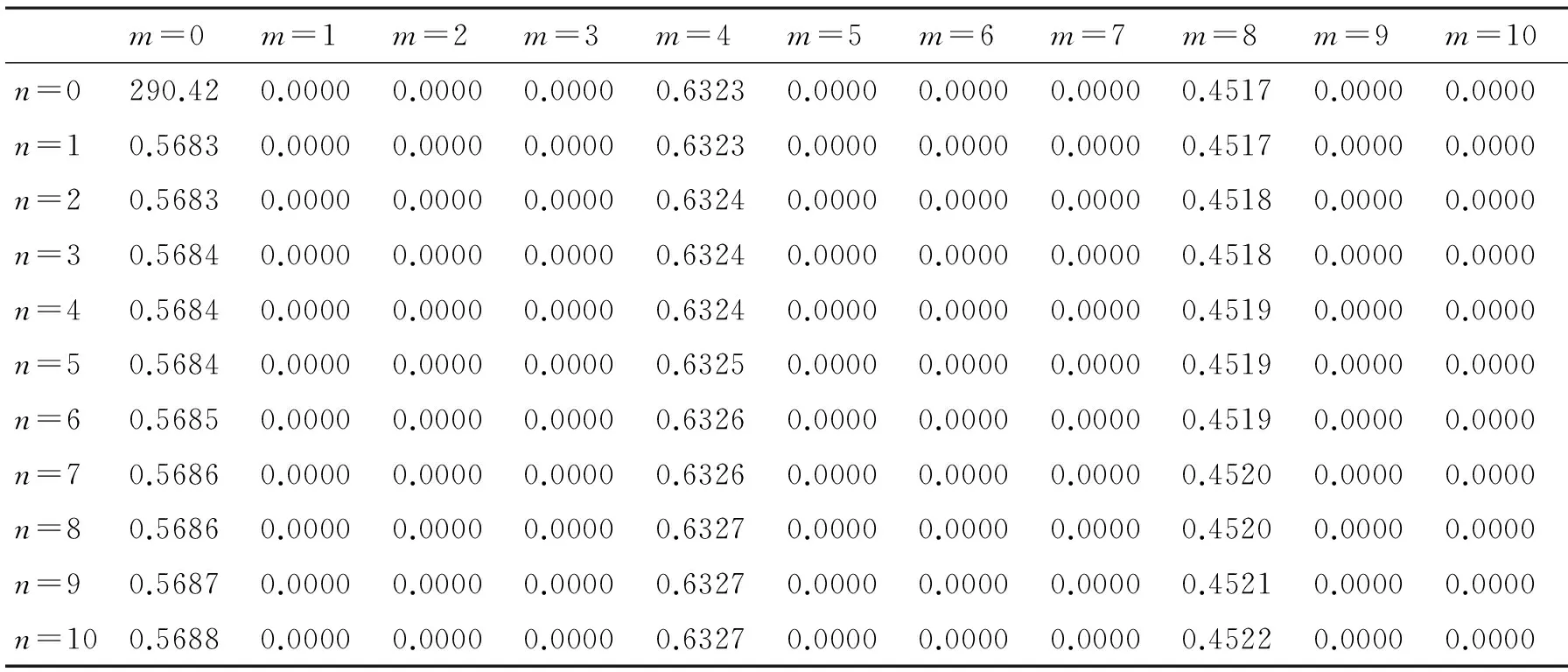
表2　恒定像素值168

3) Li[12]等给出了灰度图像的PHT矩选取规则,结合彩色图像四元数PHT精确矩的计算实验和四元数PHT鲁棒性实验,总结出四元数PHT水印嵌入最终矩的选取规则,从以下方面考虑:

(1)因为当重复度l=4m,m∈Z时,计算出的四元数PHT是不精确的,所以不能用于水印信息的嵌入。

(2)为了保证四元数PHT在其幅值中嵌入水印信息后的相关对称性,这里,选择其阶数为非负整数的四元数PHT矩。最终,用于水印嵌入的四元数PHT矩选取如下

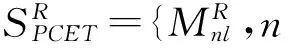
(13)

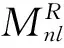
水印嵌入所选取的四元数PHT矩个数为

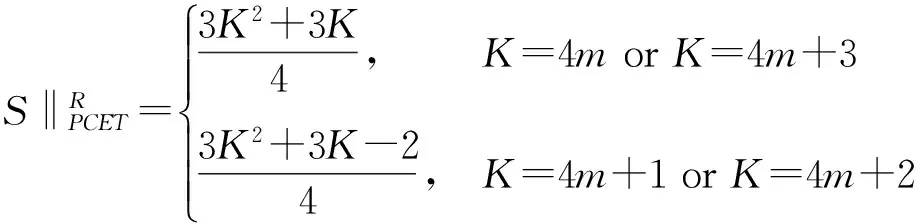
(14)

其中,K为最大阶数。

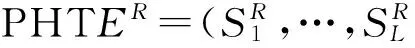
4.2数字水印信息的嵌入

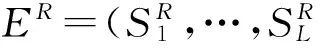
(15)

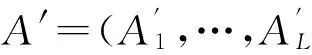
4.3含水印图像的获得

选取嵌入水印信息前后的四元数PHTER和ER′分别进行重构,得到两个重构图像,对这两个重构图像做差值运算,将得到的差值叠加到原载体图像I(x,y)中,即得到了含水印图像I*(x,y)。

5数字水印的提取算法

5.1四元数极谐变换矩的选取

5.2数字水印信息的提取

当水印检测提取时,本章算法无需原始载体提供相关数据,故属于盲水印类型,具体检测提取过程为:

1) 通过密钥key2生成量化函数d(·),并且满足d(1)=Δ/2+d(0),d(0)∈[0,1]。

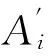
(16)

(17)

为了便于对上面公式的理解,现将式(17)分解成以下几个详细步骤:

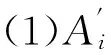
(2)计算(1)中两个距离的差值,记为t=dis0-dis1;

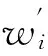
4) 对得到的一维水印图像重新转换成P*P大小的水印图像。

6仿真结果

6.1检测性能测试

利用本文所提出的算法对256×256×24bit Barbara彩色图像进行了测试,数字水印采用16×16的二值图像。图1给出了含水印图像与原始图像的差值图像,为了便于显示,差值图像像素值分别扩大5倍、10倍、20倍、50倍,表3给出了峰值信噪比(PSNR)、时间、BER等相关性能信息。

图1　Barbara含水印图像与载体图像的差值图像

ImagePSNRTime(s)嵌入提取BERBarbara47.9223277.995681159.3569310

6.2抗攻击能力测试

为了测试本算法抵抗各种常规攻击的能力,文中进行了大量测试实验,图2为受到常规信号处理后的含水印图像,以及受攻击后所提取出的数字水印信息,具体实验结果图2所示。

图2　测试图像抵抗常规信号处理的结果

图3给出了测试图像几何攻击后的含水印图像,以及受攻击后所提取出的数字水印信息。

图3　测试图像抵抗几何攻击后的结果

表4和表5给出了本文算法与文献[14]、文献[15]算法的鲁棒性对比。(这里,分母表示的含义是原始图像中一共嵌入的水印个数,分子则是攻击后依然成功检测到的水印个数)。

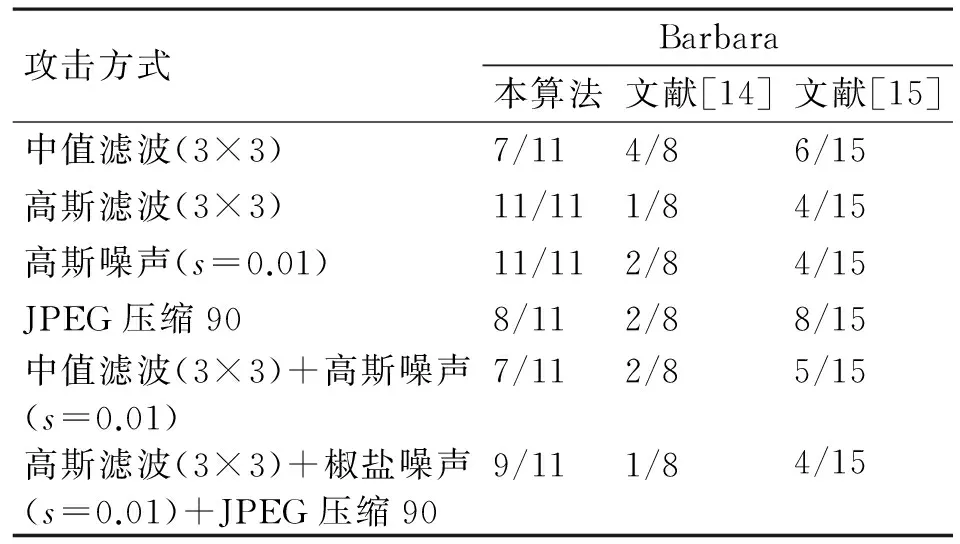
表4　常规信号处理下的数字水印检测率

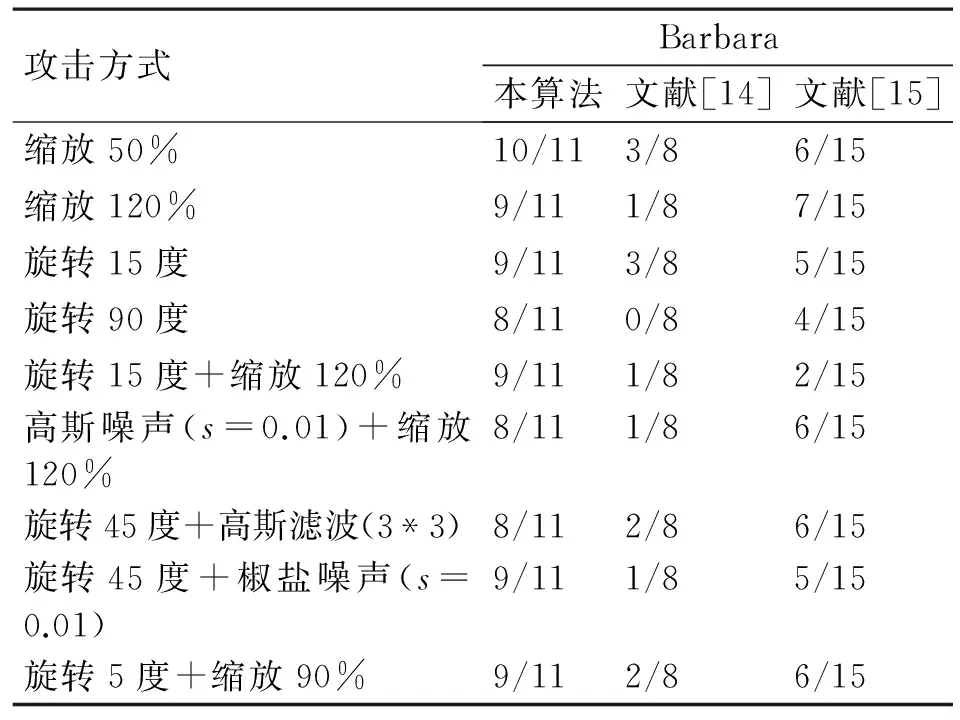
表5　几何攻击下的数字水印检测率

7结语

本算法以四元数和灰度图像极谐变换理论为基础,结合四元数极谐变换所具有的不变特性,将原始彩色图像进行了四元数极谐变换,通过选择部分稳定的变换矩从而利用量化调制的方法,完成了数字水印信息的嵌入过程,构造出了鲁棒型数字图像水印算法,从仿真实验结果能够看出,本文所提出的算法能够很好地抵抗常规攻击和几何攻击,具有较好的鲁棒性能,同时含水印图像具有较佳的不可感知性。

参 考 文 献

[1] D. Zheng, S. Wang, J. Y. Zhao. RST invariant image watermarking algorithm with mathematical modeling and analysis of the watermarking processes[J]. IEEE Trans. on Image Processing,2009,18(5):1055-1068.

[2] 江淑红.彩色图像的超复数整体处理理论及应用研究[D].上海:复旦大学,2008.

JIANG Shuhong. Research on the theory and application of the hypercomplex holistic processing of color image[D]. Shanghai: Fudan University,2008.

[3] Bas P, Nihan N L, Chassery J M. Color image watermaking using quaternion Fourier transform[C]//Proc IEEE Int Conf Acoustics, Speech and Signal Processing(ICASSP 2003),2003,Ⅲ:521-524.

[4] Ma X J, Xu Y, Song L, et al. Color image watermaking using local quaternion Fourier spectral analysis[C]//Proc 2008 IEEE Int Conf Multimedia and Expo(ICME 2008),2008:233-236.

[5] Tsui T K, Zhang X P, Androutsos D. Color image watermaking using multidimensional Fourier transforms[J]. IEEE Transactions on Information Forensics and Security,2008,3(1):16-28.

[6] Q. G. Li, M. Zhu. Quaternion Fourier-Mellin moments for color images[J]. Pattern Recognition,2011,44(2):187-195.

[7] 江淑红,张建秋,胡波.一种超复数频域的有意义数字水印算法[J],系统工程与电子技术.2009,31(9):2242-2245.

JIANG Shuhong, ZHANG Jianqiu, HU Bo. Content based image watermarking algorithm in hypercomplex frequency domain[J]. Systems Engineering and Electronics,2009,31(9):2242-2245.

[8] C. Moxey, S. Sangwine, T. Ell. Color-grayscale image registration using hypercomplex phase correlation[C]//Proceedings of the 2002 IEEE International Conference on Image Processing,2002,2:385-388.

[9] B. J. Chen, H. Z. Shu, H. Zhang, et al. Quaternion Zernike moments and their invariants for color image analysis and object recognition[J]. Signal Processing,2012,92(2):308-318.

[10] B. J. Chen, H. Z. Shu, G. Chen. Color Face Recognition Based on Quaternion Zernike Moment Invariants and Quaternion BP Neural Network[J]. Applied Mechanics and Materials,2013,2(2):1034-1039.

[11] Y. Q. Xin, S. Liao, M. Pawlak. Circularly orthogonal moments for geometrically robust image watermarking[J]. Pattern Recognition,2007,40(12):3740-3752.

[12] L. D. Li, S. S. Li, J. S. Pan. Geometrically invariant image watermarking using Polar Harmonic Transforms[J]. Information Sciences,2012,199(15):1-19.

[13] K. K. Muhammad. Research advances in data hiding for multimedia security[J]. Multimedia Tools and Applications,2011,52(3):257-261.

[14] 钟艳.基于四元数傅里叶梅林变换的RST不变彩色图像水印算法[J].计算机与现代化,2014(5):114-117.

ZHONG Yan. RST Invariant Color Image Watermarking Algorithm Based on Quaternion Fourier-Mellin Transform[J]. Computer and Modernization,2014(5):114-117.

[15] 盖琦,乔兆亮.基于离散四元数傅里叶变换的彩色图像信息隐藏技术[J].计算机应用研究,2011,28(7):2747-2749.GAI Qi, QIAO Zhaoliang. Color image steganography using discrete quaternion Fourier transforms[J]. Application Research of Computers,2011,28(7):2747-2749.

Robust Digital Watermarking Algorithm Based on Quaternion Very Harmonic Conversion

ZHANG Bo

(Department of Electronics and Information Engineering, Changsha Normal University, Changsha410100)

AbstractThis paper presents a robust digital image watermarking algorithm based on quaternion very harmonic conversion. The algorithm combines a very harmonic quaternion invariant feature transform, color image vector quaternion very harmonic conversion, after conversion, a part of a stable amplitude quaternion very harmonic transform moments is selected, and then according to the quantization modulation. The proposed algorithm selected watermark embedding quaternion get information before and after the reconstruction of two reconstructed images, then the difference between the two reconstructed images do arithmetic, the difference will be superimposed onto the original vector image, then watermarked images are gotten. Simulation results show robust digital watermarking algorithm based on quaternion very harmonic conversion can be a good resistance to conventional attacks and geometric attacks, has better robustness.

Key Wordsquaternion polar harmonic transform, digital watermarks, against geometric attack, robustness

收稿日期:2015年12月10日,修回日期:2016年1月17日

基金项目:湖南省自然科学基金项目(编号:2015JJ6007);湖南省教育厅科学研究项目(编号:15C0103)资助。

作者简介:张博,男,硕士,讲师,研究方向:模式识别、人工智能、图像处理。

中图分类号TP309

DOI:10.3969/j.issn.1672-9722.2016.06.031