基于投影寻踪的NAT识别技术

路　海　张伟燕　李　芬　王新宇

(1.中国工程物理研究院计算机应用研究所　绵阳　621900)(2.华中科技大学计算机学院　武汉　430074)

基于投影寻踪的NAT识别技术

路海1张伟燕1李芬1王新宇2

(1.中国工程物理研究院计算机应用研究所绵阳621900)(2.华中科技大学计算机学院武汉430074)

摘要随着网络的发展,网络地址转换(NAT)技术的应用越来越普及,缓解了网络IP地址枯竭的问题,然而也带来了一定的安全隐患。因此,有效地识别NAT变得十分有必要。论文提出一种基于网络流量的NAT识别技术,引入投影寻踪技术,通过网络流量特征对NAT进行识别。使用基于量子粒子群的投影寻踪算法,将量子粒子群的全局搜索能力与投影寻踪对高维数据的降维能力的结合。核心是获取网络中IP地址设备的流量特征数据,通过算法把高维数据投影到低维子空间上,从而将NAT设备与普通设备分隔开,实现NAT的识别。

关键词网络地址转换; 网络地址转换识别; 流量特征; 投影寻踪; 量子粒子群算法

Class NumberX196

1引言

网络地址转换(Network Address Translation,NAT)是一种将IP数据包中的内部私有IP地址与一个公网IP地址进行互相转换的技术,实质是通过动态维护一个映射表,将内部IP地址及端口映射到外部地址上。NAT技术有效地解决了IP地址资源匮乏的问题,同时实现了私有网络与公共网络IP地址之前的映射互访,有效地将内外网分隔开来,使得公共外网无法直接访问局域网内的主机,防范了来自公共网络的非法攻击。

NAT技术实现的方式有三种:静态地址转换(Static NAT)、动态地址转换(Dynamic NAT)以及端口多路复用(Port Address Translation,PAT)。

然而,NAT技术使得私有网络中的主机对于公共网络是透明的,无法对网络中的所有设备用户进行识别认证,对于网络的监管带来了一定的安全隐患,对网络安全带来了安全威胁。因此很有必要找到一种方法能行之有效地识别区分一个网络中是否存在NAT设备。

NAT流量识别方法[4]一般采用被动检测方法,即被动收集监听网络中的数据流量,通过数据包的首部或内容来进行NAT的检测。NAT的被动检测方法大致可以分为两类:基于TCP/IP协议特征字段的识别方法与基于应用层信息的识别方法。

传统的各种NAT识别方法依赖于IP数据包中的特殊字段,但是这些方法受到了操作系统等诸多制约。因此,本文引入投影寻踪技术,通过网络流量特征对NAT进行识别。投影寻踪分析方法[5]的基本原理:其基本思想是利用计算机技术,把高维数据通过某种组合,投影到低维(1～3维)子空间上,并通过极小化(或极大化)某个投影指标,寻找出能反映原高维数据结构或特征的投影,在低维空间上对数据结构进行分析,以达到研究和分析高维数据的目的。

使用基于量子粒子群的投影寻踪算法,将量子粒子群的全局搜索能力与投影寻踪对高维数据的降维能力的结合。核心是获取网络中IP地址设备的流量特征数据,通过算法把高维数据投影到低维子空间上,从而将NAT设备与普通设备分隔开,实现NAT的识别。

2投影寻踪技术

2.1粒子群算法

粒子算法(PSO)[12]通过个体间的竞争与合作来实现高维空间中最优解的搜索,可以解决复杂的优化问题。

PSO算法的基本思想:首先初始化粒子群体,每个粒子个体代表该优化问题的一个可行解,并且每一个粒子个体都由被优化问题的目标函数确定一个适应值。群体中每个粒子将在解空间中按一个速度决定粒子的方向和距离规则运动。然后粒子们就追随当前的最优粒子在解空间中搜索,经过多次迭代搜索,最后得到问题的最优解。在每一次迭代中,粒子通过跟踪两个“极值”来更新自己。第一个就是粒子本身所找到的最优解,这个解叫做个体极值pbest。另一个极值是整个种群目前找到的最优解,这个极值是全局极值gbest。

在找到上述两个最优值时,粒子根据如下公式更新自己的速度和新的位置:

(1)

(2)

式中,vid为粒子i飞行速度矢量的第d维分量,xid为粒子i位置矢量的第d维分量,c1、c2为常数,称学习因子,分别调节向全局最好粒子和个体最好粒子方向飞行的最大步长,rand()是[0,1]上的随机数,w为惯性权重。

式(1)右边由三部分组成,第一部分为“惯性”或“动量”部分,反映了粒子的运动“习惯”,代表粒子有维持自己先前速度的趋势;第二部分为“认知”部分,反映了粒子对自身历史经验的记忆,代表粒子有向自身历史最佳位置逼近的趋势;第三部分为“社会”部分,反映了粒子间协同合作与知识共享的群体历史经验,代表粒子有向群体或邻域历史最佳位置逼近的趋势,根据经验,通常c1=c2=2,i=1,2,…,D。vid是粒子的速度,vid∈[-vmax,vmax],vmax是常数,由用户设定用来限制粒子的速度。rand()是介于[0,1]之间的随机数。

2.2量子粒子群算法

由于在经典的PSO系统中,粒子的收敛是以轨道的形式实现的,并且又由于粒子的速度总是有限的,因此在搜索过程中粒子每个迭代步的搜索空间是一个有限的区域,不能覆盖整个可行空间。因此一般的PSO算法不能保证以概率1收敛到全局最优解,这正是一般PSO算法的最大缺陷,而在量子空间中,粒子的聚集性通过在粒子运动中心存在的某种吸引势产生的束缚态来描述,而处于量子束缚态的粒子可以以一定的概率密度出现在空间任何点,满足聚集态的性质的粒子可以在整个可行解空间中进行搜索,但不会发散到无穷远处。

量子粒子群优化算法[6]是从量子力学的角度提出的一种新的PSO算法,这个算法简单易行,不仅参数个数少,并且在搜索能力上也优于PSO算法。该算法的整个流程和基本PSO大体上相同,不同点是粒子位置的更新公式不同,如下:

p=a*pbest(i)+(1-a)*gbest

(3)

(4)

其中,a,u为[0,1]之间的随机数,mbest是粒子群pbest的中间位置,b为收缩扩张系数,在QPSO的收敛过程中线性递减,G为当前进化代数,T为最大进化代数。QPSO中粒子位置的更新按照以上公式进行,没有速度更新。

3基于投影寻踪的NAT技术识别

NAT流量识别本质上是将网络上的NAT设备与普通设备进行划分。因此,本文采用基于两子粒子群算法的投影寻踪算法,通过收集网络中IP地址的网络流量,基于流量特征进行设备划分,从而实现NAT技术识别。

3.1投影寻踪聚类方法模型

基本思想是:利用计算机技术,把高维数据通过某种线性组合投影到低维子空间,对于投影过程的构造,采用投影指标函数(目标函数)来衡量投影后保留原始数据结构特征的可能性大小,它是用于衡量投影到低维空间的数据是否有意义的目标函数,找到一个或几个投影方向,使它的指标值达到最大或最小,然后根据该投影值对高维数据聚类。其中,构造投影指标函数及优化投影方向是应用投影寻踪方法能否成功的关键[7]。

最佳投影方向即为最能够显示高维数据内部结构特征的那个方向。从信息提取的程度上来说,对数据信息保留最完整、信息利用最充分的方向就是最佳投影方向,那么,对投影方向的优化其实是找出最能反映数据特征的投影指标。如果数据的结构特征较复杂,一个投影方向难以完全表示,则允许存在反映数据整体结构的多个投影方向。总而言之,能够将高维的原始数据清晰地投影在低维空间上,并且保证投影后的数据分布结构是有意义的,能满足这个条件的投影方向都是最佳投影方向。

模型的建立:

步骤1:样本评价指标集的归一化处理

设各指标值的样本集为{x*(i,j)|i=1,2,…,n;j=1,2,…,p},其中x(i,j)为第i个样本第j个指标值,n,p分别为样本数和指标数。归一化处理如下:

对于越大越优的指标:

(5)

对于越小越优的指标:

(6)

其中,xmax(j)、xmin(j)分别为第j个指标值的最大值和最小值,x(i,j)为指标值归一化的序列。

步骤2:构造投影指标函数

Q(a)投影寻踪方法就是把p维数据{x(i,j)|j=1,2,…,p},转化为以a={a(1),a(2),a(3),…,a(p)}为投影方向的一维投影值z(i):

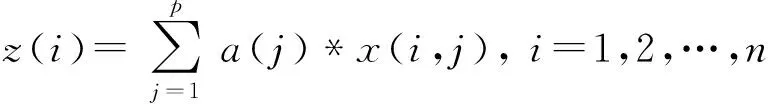
(7)

根据{z(i)|i=1,2,…,n}进行K均值聚类。要求投影值z(i)的散布特征应为:局部投影点尽可能密集,最后凝聚成若干个点团,而在整体上投影点团之间尽量散开。因此,投影指标函数为

Q(a)=Sz*Dz

(8)

(9)

(10)

其中,Sz为投影值z(i)的标准差,Dz为投影值z(i)的局部密度,E(z)为序列{z(i)|i=1,2,…,n}的平均值,R为局部密度的窗口半径,可取rmax+p/2≤R≤2p,一般取R=0.1*Sz,r(i,j)表示样本之间的距离,r(i,j)=|z(i)-z(j)|,u(t)为一单位阶跃函数,当t≥0时,其值为1,当t<0时其函数值为0。

步骤3:优化投影指标函数

当各指标值的样本集给定时,Q(a)只随投影方向a变化。不同的投影方向反映不同的结构特征,最佳投影方向就是最大可能暴露高维数据特征结构的投影方向,通过优化投影指标函数来寻找最佳投影方向,即

最大化目标函数:

Max:Q(a)=Sz*Dz

(11)

约束条件:

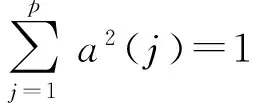
(12)

这是一个以{a(j)|j=1,2,…,p}为优化变量的复杂非线性优化问题,用传统的优化方法处理较难。本文利用几种智能优化算法的实数编码解决其高维全局寻优问题,即优化投影方向,使目标函数达到极值时,得到最佳投影方向。

步骤4:聚类

把由步骤3求得的最佳投影方向a带入式(7)后可得各样本的投影值{z(i)|i=1,2,…,n},将任意两个样本的投影值进行比较,二者越接近,表示这两个样本越倾向于分为同一类。本文引入K均值聚类算法对投影值进行聚类,投影值属于某一类,则对应的原始数据样本属于同一类别。

3.2基于投影寻踪的量子粒子群算法模型

基于QPSO的投影寻踪聚类算法采用基于投影方向的实数编码,一个编码对应了一组投影方向,而且p维的投影方向组成每个粒子的位置,因此粒子采用的编码结构为:x1x2…xp。

而且算法中,投影目标函数确定适应度f(x):

f(x)=Q(x)

(13)

约束条件处理为

(14)

算法的计算流程为:

1) 根据式(5)或(6)对原始数据进行归一化处理;

2) 随机产生满足约束条件式(12)的初始种群,根据式(13)计算每个粒子的适应度;

3) 对每个粒子,比较它的适应度值和经历过的最好位置pbest的适应度值,如果更好,更新pbest;

4) 对每个粒子,比较它的适应度值和群体所经历的最好位置gbest的适应度值,如果更好,更新gbest;

5) 根据式(4)更新粒子位置,生成新的粒子群体;

6) 对群体中的不合法个体按式(14)进行修正;

7) 如果达到结束条件(足够好的位置或最大迭代次数),则结束,否则转2)。

3.3NAT流量特征参数选取

实际网络中,NAT设备因为内部网络中具有一定数量主机,其网络流量特征相比于普通设备会有很大的不同。因此,找出合适的NAT流量特征是影响识别效果的关键因素,通过分析这些流量特征,得出实验所需的NAT流量特征参数集。

通过分析比较,可发现NAT设备具有如下流量特征:

1) 流量与报文数

由于NAT设备后具有一定数量主机,因此相比普通设备,NAT设备往往网络流量与报文数量会比较大。因此对于NAT设备流量特征,选取IP地址的流量字节数与报文数作为参数。

2) 流数目

NAT设备相比普通设备,流(即五元组)的数目总体比较多,而一台普通主机,相对来说传输的流数目较少。因此,可选取流数目作为参数。

3) 端口的数目

由于大多数NAT设备的公网IP地址较少,因此大多采用端口多路复用(PAT)的方式。在这种方式下,内部网络的多个IP地址映射到一个公网IP地址的不同端口上,因此在内部网络的主机与外部网络的通讯过程中,NAT设备往往使用多个端口,而相较而言,一台普通设备使用的端口数较少。因此流量特征参数可选用不同设备的通信端口数。

4) TCP连接数

NAT设备后由于具有一定数量的主机,因此网络的TCP连接更为频繁,总的并发TCP连接数较多。

5) DNS报文的数量

由于NAT设备后的主机访问网站数量、频率较多,因此访问不同域名时发出的DNS请求频率较高,DNS请求的报文数量也更多,而一台普通主机在一段时间内不会产生较多的DNS请求。因此可采用DNS报文数作为参数。

6) IP地址数

因为NAT设备后有较多主机,与其通信的网络设备较多,因此NAT网络流量的报文中IP地址(源、目的IP地址)相对普通设备较多,普通设备在一段时间内往往只与少数IP地址设备进行通信。因此可以选用同一IP地址通信的IP地址数作为流量特征参数。

4实验及结果分析

4.1实验数据采集

本文采用网络环境共有38台设备主机,其中有6台为NAT设备,每台NAT设备后接入4台主机组成一个NAT子网,然后NAT设备与14台普通主机共同接入一个带有镜像端口的交换机,数据采集时,交换机会自动将流经所有被镜像端口的网络数据流量复制一份到镜像端口。通过在镜像端口处连接的一台单独普通主机作为数据采集器进行网络流量数据采集。

本文的数据是通过在数据采集器端使用yaf和silk软件进行采集分析的。Yaf将镜像端口获得的网络流数据转换成IPFIX流文件,然后交由silk工具处理,输出silk流文件,并以二进制格式写入文件。然后通过silk工具的rwfilter命令进行参数过滤。

根据上文总结,本文采用数据集中六个流量特征值作为实验参数,如表1所示。

表1　NAT流量特征参数

4.2结果分析

本次实验收集了24h内网络中的数据流量,通过使用基于量子粒子群算法的投影寻踪算法得到的投影值如图1所示。

图1　投影值

图1中横坐标表示设备编号,其中1～6号为NAT设备,7～20号为普通设备。纵坐标为每个设备的数据参数投影值。可以从图中看出,通过投影,将NAT设备和普通设备进行了划分,从而能够快速找出NAT设备。

当然,算法还是可能受到诸多方面的影响,例如网络环境中可能出现普通主机的流量特征值较大的情况,但是,在设备数量较多、网络稳定、数据采集时间长的情况下,算法依然能够较为准确地进行NAT识别。

5结语

随着网络的迅速发展,NAT技术的运用越来越普及。在NAT技术带来便利的同时,也带来了安全隐患。因此,如何在网络中识别出NAT设备变得十分有必要。

本文针对现有的NAT识别方法普遍依赖于IP数据包中的特殊字段等缺点,引入投影寻踪技术,通过网络流量特征对NAT进行识别。使用基于量子粒子群的投影寻踪算法,将量子粒子群的全局搜索能力与投影寻踪对高维数据的降维能力的结合。核心是获取网络中IP地址设备的流量特征数据,通过算法把高维数据投影到低维子空间上,从而将NAT设备与普通设备分隔开,实现NAT的识别。

本文在投影寻踪聚类模型中引入量子粒子群算法(QPSO),使两者有机结合,充分利用QPSO的全局快速收敛性和投影寻踪聚类模型的降维能力,有效解决了高维数据聚类计算量大效率低的问题,使其优势互补。并通过实验对收集的数据进行了基于量子粒子群算法的投影寻踪算法,将投影值投影到二维坐标轴进行分析。实验结果表明该方法能够有效地识别NAT设备。

参 考 文 献

[1] P. Srisuresh, M Holdrege. IP Network Address Translator(NAT) Terminology and Consideration[S]. RFC2663,1999-08.

[2] P. Srisuresh, K. Egevang. Traditional IP Network Address Tranlator(Traditional NAT) RFC3022, Internet Engineering Task Force, January 2001, 2001.

[3] Zhu Hongliang, Li Rui. An Integrative Model and System for Detecting NATted Hosts[C]//ICIECS2009, Wuhan, China. Dec. 2009.

[4] 谭超.现代NAT检测技术的原理与应用[J].仪器仪表用户,2006,13(5):130-133.

TAN Chao. The principle and application of modern NAT detect technology[J]. Electronic Instrumentation Customer,2006,13(5):130-133.

[5] 付强,赵小勇.投影寻踪模型原理及其应用[M].北京:科学出版社,2006.

FU Qiang, ZHAO Xiaoyong. The principle and application of Projection Pursuit Model[M]. Science Press,2006.

[6] 张群,雷秀娟,马千知.量子粒子群在投影寻踪聚类中的应用[J].计算机工程与应用,2011,47(2):190-193.

ZHANG Qun, LEI Xiujuan, MA Qianzhi. Application of Quantum-behaved Particle Swarm Optimization in projection pursuit clustering[J]. Computer Engineering and Applications,2011,47(2):190-193.

[7] 王李近,胡欣欣,宁正元.基于粒子群优化的投影寻踪聚类模型及其应用[J].南京信息工程大学学报,2010,2(4):320-323.

WANG Lijin, HU Xinxin, NING Zhengyuan. Projection pursuit cluster model based on particle swarm optimization and its application[J]. Journal of Nanjing Unviersity of Information Science & Technology,2010,2(4):320-323.

[8] 朱应武,杨家海,张金祥.基于流量信息结构的异常检测[J].软件学报,2010,21(10):2573-2583.

ZHU Yingwu, YANG Jiahai, ZHANG Jinxiang. Anomaly Detection Based on Traffic Information Structure[J]. Journal of Software,2010,21(10):2573-2583.

[9] Lakhina A, Crovella M, Diot C. Mining anomalies using traffic feature distributions[C]//Proc. of the 2005 Conf. on Applications, Technologies, Architectures, and Protocols for Computer Communications. Pennsylvania,2005:217-228.

[10] G Tsirtsis, P Srisuresh. Network Address Translation-Protocol Translation(NAT-PT)[S]. RFC2766,2000-02.

[11] 龙海峡,须文波,孙俊.基于QPSO的数据聚类[J].计算机应用研究,2006(12):40-45.

LONG Haixia, XU Wenbo, SUN Jun. Data Clustering Based on Quantum-behaved Particle Swarm Optimization[J]. Application Research of Computers,2006(12):40-45.

[12] 段晓东,王存睿,刘向东.粒子群算法及其应用[M].沈阳:辽宁大学出版社,2007.

DUAN Xiaodong, WANG Cunrui, LIU Xiangdong. Particle Swarm Optimization and Application[M]. Shenyang: Liaoning University Press,2007.

[13] 田铮,林伟.投影寻踪方法与应用[M].西安:西北工业大学出版社,2008.

TIAN Zheng, LIN Wei. Projection Pursuit Method and Application[M]. Xi’an: Northwestern Polytechnical University Press,2008.

NAT Identification Technology Based on Projection Pursuit

LU Hai1ZHANG Weiyan1LI Fen1WANG Xinyu2

(1. Institute of Computer Application, Chinese Academy of Engineering Physics, Mianyang621900)(2. School of Computer Science & Technology, Huazhong University of Science and Technology, Wuhan430074)

AbstractWith the development of network, network address translation(NAT) technology is more and more widly applied, which relieves the problem of network IP address exhaustion, and brings some potential risk. Therefore, the effective identification of NAT become very necessary. This paper proposes a NAT identification technology based on network flow, introducing the projection pursuit technique, analysising on the characteristics of network flow to identify NAT. Using projection pursuit based on quantum particle swarm algorithm, combing the quantum particle swarm global search ability and the high-dimensional data dimension reduction ability of the projection pursuity. Core is to obtain the feature data of the network equipment flow, using the algorithm to project the high-dimensional data to low-dimensional subspace, which will separate the pervasive devices and the NAT devices, to achieve the identification of NAT.

Key WordsNAT, NAT detection, network flow feature, projection pursuit, quantum particle swarm optimization

收稿日期:2015年12月10日,修回日期:2016年1月26日

作者简介:路海,男,研究员,研究方向:计算机网络和信息安全。张伟燕,男,硕士,高级工程师,研究方向:数据库技术和信息安全。李芬,女,博士,高级工程师,研究方向:网络和信息安全。王新宇,男,硕士研究生,研究方向:网络和信息安全。

中图分类号X196

DOI:10.3969/j.issn.1672-9722.2016.06.027