基于多层次模糊综合评判及模糊理论的设备维修研究

余忠礼　王晓东

(1.昆明理工大学信息工程与自动化学院　昆明　650500)(2.云南省矿物管道输送工程技术研究中心　昆明　650500)

基于多层次模糊综合评判及模糊理论的设备维修研究

余忠礼1,2王晓东1,2

(1.昆明理工大学信息工程与自动化学院昆明650500)(2.云南省矿物管道输送工程技术研究中心昆明650500)

摘要针对矿浆管道关键设备维修情况复杂的问题,提出了以多层次模糊综合评判的方法来确定设备的维修方式,以模糊理论的方法来确定设备的维修周期。并且以单向阀设备为研究对象,预测了其最佳维修方式及最佳维修周期,实际生产表明,该方法对设备维修具有一定的指导意义。

关键词矿浆管道关键设备; 模糊理论; 维修方式; 维修周期

Class NumberTP391

1引言

长期以来,我国对设备的维修方式主要是采用事后维修与定期维修两种方式,而且决定采取何种维修方式都是依据经验来决定,这种方式在早期的工业生产中对于设备的维修指导起到了很好的作用,但是随着工业技术的发展,单个设备自身的复杂性越来越高,不同设备之间组合后复杂性越来越高,根据经验判定设备的最佳维修方式越来越困难。对于廉价以及对生产影响不大的设备仍然可以采用事后维修方式,但是对于其它的设备,如果全部采用定期维修可能存在维修过度或者维修不足的问题,造成资源浪费或者使得设备安全性降低,更严重的是会造成人员伤亡[1]。

以可靠性为中心的维修(RCM)是目前被广泛接受的一种先进的设备维护模式,它具有以最小的资源消耗保证最大的可靠性与安全性的特点[2]。有学者已经以经济性为原则对设备的维修周期做了研究[3～4],也有其他学者以可靠性、费用等为目标量进行了相应的研究[5～6]。维修策略有很多种[7],针对不同的环境需要选取合适的维修策略。在矿浆管道运输过程中,由于许多重要设备结构比较复杂、设备故障影响因素众多,设备的最佳维修方式难以确定或者不够科学。传统的专家评判模型对于影响因素较多的系统在权重分配上存在不合理性,而多层次模糊综合评判的方法是一种典型的定性与定量相结合的评判方法,能够对影响因素模糊、影响因素多以及影响因素需要分层的系统做出良好的评判[8],因此很适合用于对矿浆管道关键设备的研究。对于需要进行预防维修的设备来说,最重要的问题就是合理确定预防维修周期,维修周期的不合理往往会造成维修成本的增加,模糊理论是一种比较成熟的方法了[9～10],采用这种方法可以预测出最佳的维修周期。

2维修方式的确定

目前使用比较广泛的维修方式有事后维修、定期维修与状态维修,而影响因素主要是可靠性、维修性与经济性,对于复杂的设备来说,影响因素还具有层次之分。多层次模糊综合评判的方法的思想是:先对低层次的因素进行评判,然后依次往上进行评判,最后得出评价结果。以单向阀为例子进行分析,其设计步骤包括以下步骤:

Step1确定因素集合U:对单向阀设备来说,其主要性能因素包括三个方面,其表示方式如下:U={ui(性能因素i)/i=1,2,3},其中u1为可靠性,u2为维修性,u3为经济性,而各性能因素包含不同的评价因素。具体信息如表1所示。

表1　第一层判断矩阵

Step2确定因评语集V:评语集在这里指维修方式,单向阀设备的维修方式也是常用的三种方式之一,评语集V={v1,v2,v3},且v1为事后维修,v2为定期维修,v3为状态维修。

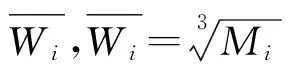
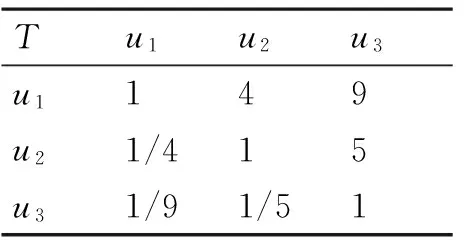
表2　第一层判断矩阵

根据表1的数据可以得到判断矩阵P,

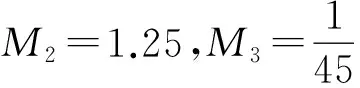
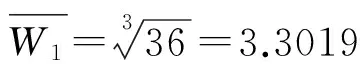
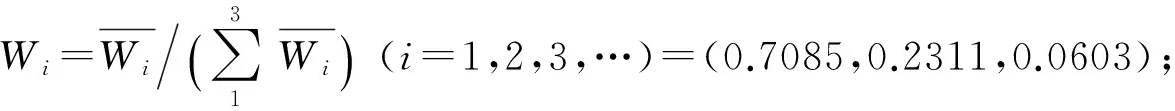
Step4进行一致性检验。

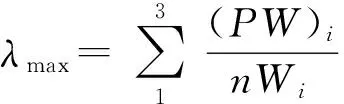
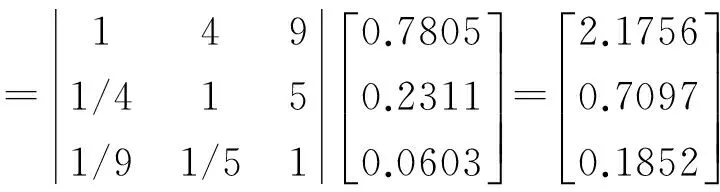
根据前面的公式可得λmax=3.0709,CI=0.0358,CR=0.0612,可知CR<0.1,矩阵P满足一致性要求。同理算出第二层的权重集A1,A2,A3,并构造第二层的模糊评判矩阵R1,R2,R3,计算出相应的权重集,采用模型M(·,⊕)进行计算得:B1=A1∘R1,B2=A2∘R2,B3=A3∘R3,则第一层的模糊评判矩阵为R=[B1B2B3]T,由于第一层的权重集A=(W1,W2,W3)已经求出,因此,由B=A∘R可以求出评判结果B。由于第二层计算步骤与第一层相同,只是数据不同而已,这里不再赘述,最后得到的结果B=(b1,b2,b3),根据最大隶属度原则,即可确定单向阀的维修方式。对于单向阀设备来说,通过前面的步骤计算可得b2最大,即单向阀的维修方式推荐采用定期维修,同理可得到电机、主泵等设备的维修方式。

3维修周期的确定

以单向阀为例,其维修方式是定期维修,如果维修周期时间过短,可能要频繁的停机检修影响生产效益,也对设备自身造成一定的损伤,而维修周期过短可能会在运行过程中出现故障,这将会对生产造成更大的损失。

针对上述问题,有人以可靠性、费用率等为优化目标对维修周期做了相关研究,以基本的维修模型和相关的基本公式为基础,结合实际设备的相关参数,能够得到一些结论。

以可靠性为目标进行分析,其每一周期T内的平均不能工作时间(Mean Down Failure,MDT)为

(1)

其中Tp为平均预防维修时间,Tf为平均修复维修时间,λ(t)为故障率。

(2)

其中MUT为平均可能工作时间。

通过对实际T求导就可以得到:

(3)

然后根据设备寿命服从的分布类型就可以确定维修周期了。

但是实际生产中由于参数复杂,难以求解,因此可以采用维修系数最小值来求解。

(4)

其中α是维修系数是指平均不能工作时间MDT与平均可工作时间MUT之比。

将己知的可靠性数据以及寿命值计算出在不同的可用度下的维修系数α值,并画成曲线,找出曲线中α值的最小点,即可确定最佳预防维修周期。

(5)

由上面的公式可知为了使可用度A最大,必须令a最小,这样可以得到最佳维修时间。

以费用最小为目标进行分析时,公式基本一样,只需要将可用度A换成费用C,维修系数α换成费用系数c,同样可以得到最佳维修时间。

4结语

不同的设备由于其性能与工作环境的关系,其维修方式与维修周期必然不同。文章采用多层次模糊综合评判及模糊理论对单向阀设备进行了研究,建立了求解最佳维修方式与维修周期的模型,也为其它设备的维修研究提供了一些指导。

参 考 文 献

[1] 叶铁丽,林金钟.煤矿机电设备维修管理模式初探[J].中国煤炭,2000,26(9):13-15,50.

YE Tieli, LIN Jinzhong. Coal mechanical and electrical equipment maintenance management mode study[J]. Journal of China Coal,2000,26(9):13-15,50.

[2] 王娟,周炳海.基于RCM的设备维护方法[J].机械,2011,38(2):8-11.

WANG Juan, ZHOU Binghai. The method of equipment maintenance based on RCM[J]. Mechanical,2011,38(2):8-11.

[3] 徐丹,吴俊.基于RCM的设备维修管理平台研究与开发[J].计算机与数字工程,2011,39(12):66-68.

XU Dan, WU Jun. Research and development of equipment maintenance management platform based on RCM[J]. Computer and Digital Engineering,2011,39(12):66-68.

[4] 尤晨,张新民.基于运行费用最小原则的综机设备最佳维修周期的优化模型[J].煤矿机械,2001(12):52-54.

YOU Chen, ZHANG Xinmin. The optimization model of best maintenance period of the fully machine equipment based on the rule of minimum running costs[J]. Coal Mining Machinery,2001(12):52-54.

[5] 贾希胜,程中华.以可靠性为中心的维修(RCM)发展动态[J].军械工程学院学报,2002,14(3):31-5.

JIA Xisheng, CHENG Zhonghua. Reliability centered maintenance(RCM) developments[J]. Journal of Ordnance Engineering College,2002,14(3):31-5.

[6] Frangopol, D. M., Kallen, M. J., Noortwijk, J. M. V. Probabilistic models for life-cycle performance of deteriorating structures review and future directions[J]. Progress in Structural Engineering and Materials,2004(6):197-212.

[7] Wang, H. A survey of maintenance policies of deteriorating systems[J]. European Journal of Operational Research,2002(139):469-489.

[8] 兰继斌,徐扬,霍良安,等.模糊层次分析法权重研究[J].系统工程理论与实践,2006(9):107-112.

LAN Jibin, XU Yang, HUO Liangan, et al. Fuzzy ahp weight study[J]. Journal of Systems Engineering Theory and Practice,2006(9):107-112.

[9] 郑圆圆,陈再良.模糊理论的应用与研究[J].苏州大学学报(工科版),2011,31(1):52-58.

ZHENG Yuanyuan, CHENG Zailiang. The application of fuzzy theory and research[J]. Journal of Suzhou University(Engineering),2011,31(1):52-58.

[10] 曹柬,周根贵,张定岳.一种基于AHP和模糊理论的多方案综合评价方法[J].浙江工业大学学报,2003,31(4):1-5.

CAO Jian, ZHOU Gengui, ZHANG Dingyue. A multiple scheme comprehensive evaluation based on AHP and fuzzy theory method[J]. Journal of Zhejiang University of Technology,2003,31(4):1-5.

Maintenance Research of Equipment Based on Multi-level Fuzzy Comprehensive Evaluation Method and Fuzzy Theory

YU Zhongli1,2WANG Xiaodong1,2

(1. Faculty of Information Engineering and Automation, Kunming University of Science and Technology, Kunming650500)(2. Engineering Research Center for Mineral Pipeline Transportation of Yunnan Province, Kunming650500)

AbstractThe maintenance of slurry pipeline key equipment is complex, a method has been proposed, adopting the multi-level fuzzy comprehensive evaluation method to determine maintenance mode of equipment, adopting the fuzzy theory to determine maintenance cycle of equipment, and then predicting the best maintenance mode and maintenance cycle by analyzing the check valve. The actual production shows that the method has certain guiding significance for equipment maintenance.

Key Wordsslurry pipeline key equipment, fuzzy theory, maintenance mode, maintenance cycle

收稿日期:2015年12月13日,修回日期:2016年1月30日

作者简介:余忠礼,男,硕士研究生,研究方向:视情维修、故障诊断。王晓东,男,博士,教授,研究方向:图像处理、基于数据驱动的工业过程控制、多源信息融合技术以及基于数据挖掘的智能检测技术。

中图分类号TP391

DOI:10.3969/j.issn.1672-9722.2016.06.013