基于TLS-LASSO算法基矩阵自适应校正的稀疏空时自适应处理

王亚莉　贾宏进

(1.91404部队　秦皇岛　066001)(2.91336部队　秦皇岛　066001)

基于TLS-LASSO算法基矩阵自适应校正的稀疏空时自适应处理

王亚莉1贾宏进2

(1.91404部队秦皇岛066001)(2.91336部队秦皇岛066001)

摘要机载预警雷达杂波抑制的STAP算法所需平稳快拍数过多,在实际环境中由于地物散射特性的快变很难得到足量训练样本,通过引入稀疏恢复可以大大减少杂波估计所需快拍数。然而,在稀疏恢复估计杂波空时谱的过程中,基矩阵的空时频率和杂波真实的空时频率之间会有不匹配现象,即off-grid问题。off-grid会严重影响稀疏恢复估计空时谱的性能。论文提出了一种基于总体最小二乘-LASSO方法的基矩阵空时频率自适应校正方法,可以较好解决off-grid问题。该算法在估计稀疏空时谱的同时对基矩阵中每一个导引矢量的空时频率进行自适应校正,从而寻找到与真实杂波位置相匹配的基向量,进而求得对应的稀疏空时谱,避免了off-grid问题带来的稀疏恢复性能下降问题。仿真实验表明论文所提算法具有较好的恢复性能。

关键词机载预警雷达; 空时二维自适应处理; 稀疏恢复; off-grid; 基矩阵自适应校正; 空时谱估计

Class NumberTN958.92

1引言

机载预警(Airborne Early Warning,AEW)雷达的主要功能是探测低空运动目标,为己方提供空中预警[1]。AEW雷达一般工作于斜下视状态,在这种工作状态下,地面回波往往具有相比目标更强的能量,强地杂波会将小目标掩盖而使得目标检测难以实现。因此,地杂波抑制是机载预警雷达中一个非常重要的课题。

空时自适应处理(Space-Time Adaptive Processing,STAP)是AEW雷达杂波抑制和动目标检测的一种重要手段[2]。但传统的STAP方法面临着训练协方差矩阵所需平稳快拍数过多、实际环境难以满足的问题。因此有学者将稀疏恢复(Sparse Recovery)这一信号处理领域中的新理论和新方法引入到STAP中,充分利用稀疏恢复在欠采样和小样本条件下信号估计的优势,试图解决传统STAP方法训练样本不足的问题,提出了基于稀疏恢复的STAP方法[3]。该方法将杂波协方差矩阵估计问题的关键步骤转化为一个稀疏空时谱的估计问题。

但是,稀疏恢复方法作为一种参数化的估计手段,有其固有的问题。其中最突出、对估计性能影响最明显的一个问题就是off-grid问题。off-grid问题是指稀疏恢复的基矩阵中,每个基向量的空时频率是人为指定的,它们和杂波源真实的空时频率并不一定匹配,由此带来稀疏恢复性能的下降。

本文提出了一种基于总体最小二乘和LASSO算法的稀疏恢复方法TLS-LASSO,可以在估计稀疏空时谱的同时,可以自适应校正基矩阵,得到正确的杂波源空时频点。仿真实验表明该方法效果较好,能够显著改善稀疏空时自适应处理的性能。

2稀疏空时自适应处理方法

2.1自适应处理与STAP

自适应处理方法是雷达信号处理中应对干扰的一种有效手段。这种方法的基本思想是,通过对环境、干扰的采样数据进行学习和训练,得到关于干扰的统计信息或特征参数,进而设计能够将干扰滤除的自适应滤波器,对包含了潜在目标和干扰的采样数据进行滤波操作[4]。经过自适应滤波器的滤波操作,输出数据中就滤除了干扰信息而仅剩目标信息。在输出数据上做检测就能有效降低干扰对检测性能的影响[5]。

对AEW雷达来说,强地杂波是主要的干扰来源。因此也可以采用上述抑制干扰的自适应处理方法来抑制地杂波。对于一维的情形,自适应阵列处理理论保证了可以在干扰所在的空间角度位置形成凹陷,从而形成针对干扰的自适应滤波器;对于动目标检测来说,MTI和MTD理论保证了可以自适应滤除多普勒域上的干扰,同时在检测出动目标。但是,由于AEW雷达位于机载平台上,载机的运动导致地面静止的杂波散射体具有相对载机平台的运动速度,并且杂波散射体的角度和其相对运动速度(对应多普勒频率)具有一定的耦合关系,在主波束照射到的范围内地杂波在角度和多普勒维度都会展宽,覆盖可探测目标的角度或速度。这样,无论在阵列(即角度)维还是在脉冲(即多普勒或速度)维都无法将地杂波和目标区分开来。因此,对于AEW雷达,抑制地杂波的自适应操作必须联合空域(角度)和时域(多普勒),在空时二维进行。这就是空时自适应处理(Space-Time Adaptive Processing,STAP)的基本思想[6～7]。

2.2稀疏STAP方法

在自适应处理中,对抑制对象统计特性或特征参数的获取是通过大量满足平稳假设的样本进行训练得到的。一个最典型的做法就是首先获取满足平稳(即独立同分布)条件的若干个采样样本向量,然后求其自相关矩阵。如果训练样本满足零均值条件,则该自相关矩阵可以认为是对样本数据协方差矩阵的一个估计。前人的工作已经证明,当训练样本数满足大于2倍的系统自由度时,用这样的方法获得的协方差矩阵估计才是有效的[2]。

在STAP中,训练样本是沿着距离向获得的。用上面所述的统计方法估计杂波协方差矩阵时,要求平稳训练样本数不小于系统自由度,假设系统的线性阵列天线有N个阵元,一个CPI内有M个脉冲,那么系统自由度为NM,则要求满足独立同分布的样本数要不小于2NM。但是,在实际环境中,由于地物散射特性的变化,距离向上杂波散射体并不严格满足平稳条件,甚至起伏很大;而且实际系统的系统自由度一般较大(尤其是一个CPI内的脉冲数可能达到上百之多),这样就要求有大量的平稳训练样本。这显然是难以满足的。因此如何减少估计杂波特性所需的平稳训练样本数就成为STAP中的一个重要课题。

稀疏恢复是信号处理领域最近十年来一个重要的突破性的进展[8]。如果一个信号在某个域是稀疏的,即只有少量元素是有显著值的,那么就可以通过稀疏恢复算法,从其压缩观测中恢复出原始信号。为了解决前面所提到的传统STAP方法训练样本不足的问题,有学者提出了基于稀疏恢复的STAP方法,即SR-STAP[9]。

假设系统由N个阵元,一个CPI内有M个脉冲,那么,空域导引矢量和时域导引矢量分别为

as=[1,exp(j2πKθ),…,exp(j2π(N-1)Kθ)]

(1)

at=[1,exp(j2πfd),…,exp(j2π(M-1)fd)]

(2)

其中Kθ=d/λsinθ。那么空时导引矢量为

a=as⊗at

(3)

向量化的空时快拍x可以写成空时导引矢量的线性组合

(4)

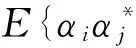
(5)

其中,σi=E{|αi|2}为杂波散射源的平均(后向)散射能量。于是,如果能够得到每一个杂波散射源的平均后向散射能量,那么就可以估计出协方差矩阵。将杂波的平均后向散射能量排列成一个二维矩阵,我们称之为空时功率谱。由于功率谱和幅度谱的众所周知的对应关系,也可以先估计杂波的平均后向散射强度,将平均后向散射强度排列而成的矩阵称为杂波的空时幅度谱,简称为空时谱。所以,杂波协方差矩阵估计问题就转化为杂波空时谱估计问题。将式(4)重写为矩阵形式:

x=Φα+n

(6)

则α就是向量化的空时频谱。由于机载AEW雷达杂波的角度和多普勒频率之间众所周知的杂波脊线关系:

(7)

很容易证明,杂波在空时(频域)平面上,即角度-多普勒平面上,是仅仅分布在杂波脊线上的,在空时频域平面内杂波是稀疏的,也就是说向量α是一个稀疏向量[11]。那么,就可以用稀疏恢复算法来通过式(6)估计杂波的空时谱,进而估计杂波协方差矩阵。这就是基于稀疏恢复的空时自适应处理方法(SR-STAP)的基本框架。可以看出,采用了稀疏恢复之后,估计杂波协方差矩阵所需的快拍数显著下降。

3TLS-LASSO-STAP方法

3.1off-grid问题

在前面所介绍的SR-STAP方法中,基矩阵中空时导引矢量的空时频点都是人为指定的,即在角度-多普勒平面上,有一个人为预设的离散化网格。但是,真实的杂波散射源所对应的角度和多普勒频率并不一定完全落在人为预设的网格上,这就是格点失配问题,即off-grid问题[12]。off-grid问题会给稀疏恢复估计空时谱带来严重的性能下降[13]。

[θ1,θ2,…,θNs],[fd1,fd2,…,fdNd]

(8)

对于某个杂波散射体对应的多普勒频率和角度,用与其邻近的fdi和θi和相应的多普勒误差Δfdi、角度误差Δθi的和来表示:

(fd,θ)=(fdi+Δfi,θi+Δθi)

(9)

那么真实杂波对应的空时导引矢量就变成如下形式:

(10)

可见在导引矢量的每一项中都含有未知参数。进而,基矩阵就变为参数化的,其中每一列也就是每一个空时导引矢量中都含有与格点失配误差相关的参数,稀疏恢复估计空时谱问题就变成了这样一个参数化稀疏恢复问题:

x=Φ(Δfd,Δθ)α+n

(11)

其中参数化的基矩阵具体形式为

Φ(Δfd,Δθ)=[a1(Δfd1,Δθ1),…,ai(Δfdi,Δθi),…,

aNc(ΔfdNc,ΔθNc)]

(12)

以上就是稀疏空时自适应处理中off-grid问题的基本描述。

3.2TLS-LASSO-STAP方法

对于这样一个问题,我们的思路是设计一个算法,在稀疏恢复估计空时谱的同时,在线估计角度误差参数和多普勒误差参数Δfdi、Δθi。这就相当于在进行稀疏恢复的同时对基矩阵进行校正。直观上,可以看做根据采样数据自适应调整基矩阵中的空时“格子”。

对于基矩阵中某一列导引矢量的第n项,假设其角度误差Δθ和多普勒误差Δfd都很小,那么,

这块石头不但不美观，而且还经常挡着别人的道路，大家都嫌弃它，看到它都绕着走。我一看到这块石头就想吐，因为它的身上经常有蜘蛛丝和其他动物的口水。看来这块石头真的是毫无用处，要提醒保安爷爷把它弄走。

exp(j2πm(fd+Nfd))≈exp(j2πmfd)(1+j2πmΔfd)

(13)

(14)

所以,对于空时导引矢量的某一项,有

(15)

其中,省略了二阶无穷小项ΔθΔfd。所以,对于空时导引矢量,可以得到:

a′=ae(1+Δa)=a+aeΔa

(16)

其中导引矢量误差项:

(17)

记如下的一个复合导引矢量矩阵为

(18)

那么空时导引矢量进一步可以写成:

(19)

从而真实的基矩阵也可以写成预设基矩阵和误差矩阵的和的形式,

Φ′=Φ+ΔΦ

(20)

其中,误差矩阵

ΔΦ=BQ

(21)

其中B=[B1,…,BNc]NM×2Nc,矩阵Q为误差变量构成的矩阵,其形式为:

(22)

至此,将需要求解的误差变量从指数项和指数项中的三角函数项中全部提出并置于矩阵Q中,并且和确定矩阵B做线性相乘。式(11)所表示参数化稀疏恢复问题变为如下的含有基矩阵加性误差项的稀疏恢复问题:

x=(Φ+ΔΦ)α+n

(23)

最终希望求解off-grid问题,同时得到稀疏空时谱的估计和空时频率误差的估计。对于稀疏空时谱估计,采用经典的l1范数最小化方法,求解LASSO问题[14]。而误差项又在基矩阵表现为加性误差,所以,考虑引入总体最小二乘(Total Least Square,TLS)方法[15]。所以,建立如下的总体最小二乘-LASSO(TLS-LASSO)优化问题:

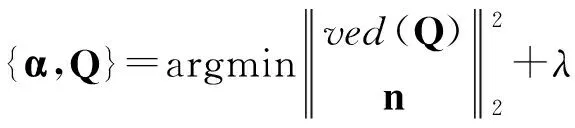
s.t.x=(Φ+BQ)α+n

(24)

上述问题没有闭式解,只能通过迭代方式求得近似解。在迭代的每一步中,分别求对稀疏空时谱α和误差矩阵Q的估计。可以证明,当固定α时,原优化问题退化为

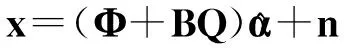
(25)

这是一个关于Q的凸优化问,可以通过凸优化工具包cvx来求解。而当Q固定时,原问题退化为一个关于的常规LASSO问题:

(26)

这仍然是一个凸优化问题,可以通过相关工具包求解。

所以,最终在式(25)和式(26)之间反复迭代,直到满足收敛条件,就得到了关于稀疏空时谱和空时频率误差的估计。这样,同时实现了空时谱估计和基矩阵自适应校正。

4仿真实验

通过产生杂波数据对本文所提算法进行仿真实验。在仿真实验中设置仿真参数如表1所示。

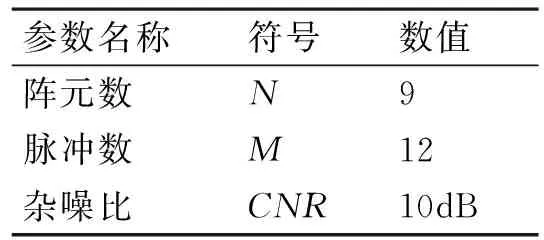
表1　仿真参数设置

分别设置两个、七个杂波散射源,对比未经过基矩阵校正的LASSO方法和TLS-LASSO方法的稀疏空时谱估计结果。

图1、图2分别展示了两个和七个杂波散射源的对比实验结果。图中横坐标为归一化的多普勒频率,纵坐标为角度,整个图所表示的空时频谱。上图为TLS-LASSO的校正结果,绿色的点代表预设的基矩阵空时频点网格,蓝色的点代表对真实杂波源估计而校正之后的空时频点位置。下图为未经基矩阵空时频率校正的LASSO算法的结果,可见,未经基矩阵校正的估计有严重的空时谱扩散现象,使得估计精度严重下降;而经过TLS-LASSO基矩阵空时频率校正之后,真实杂波源附近的基向量的空时频率能够较好的匹配杂波源的真实空时频率,空时谱估计扩散的现象得到消除,估计精度大为提高。

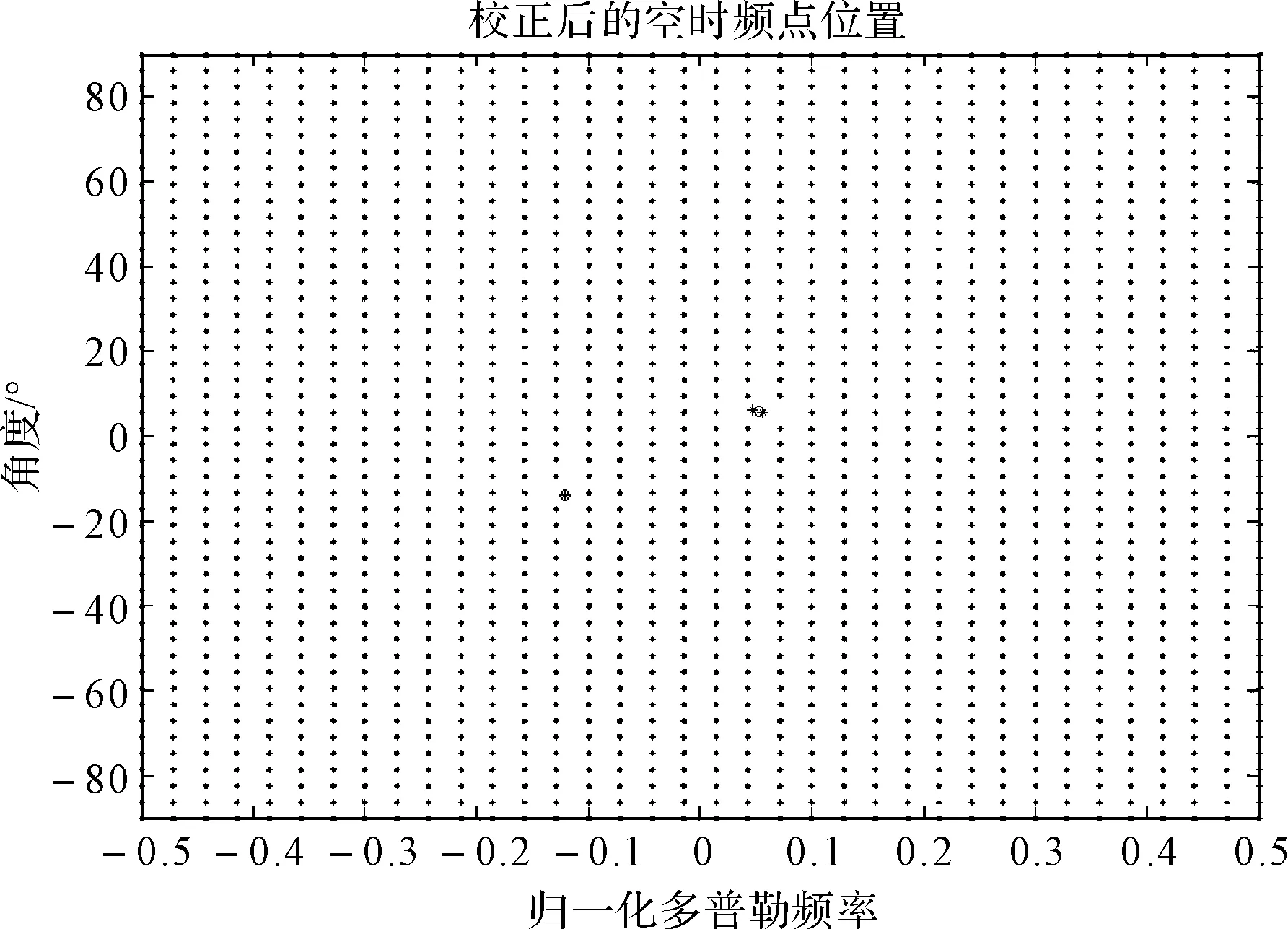
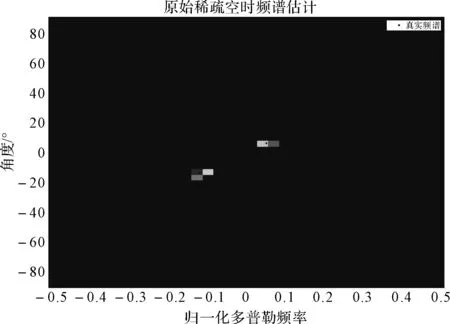
图1　基矩阵校正结果示意(两个杂波散射源)

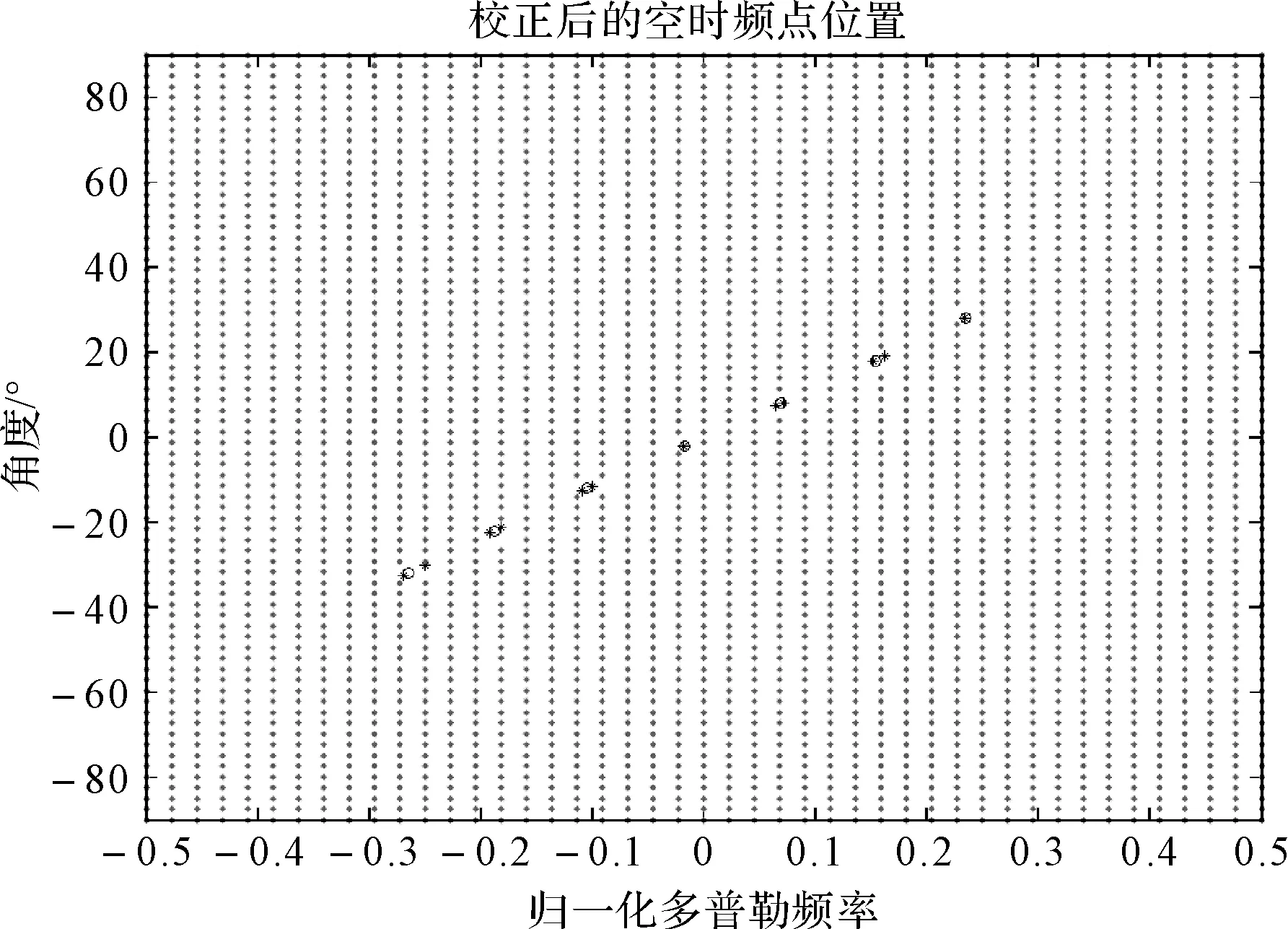
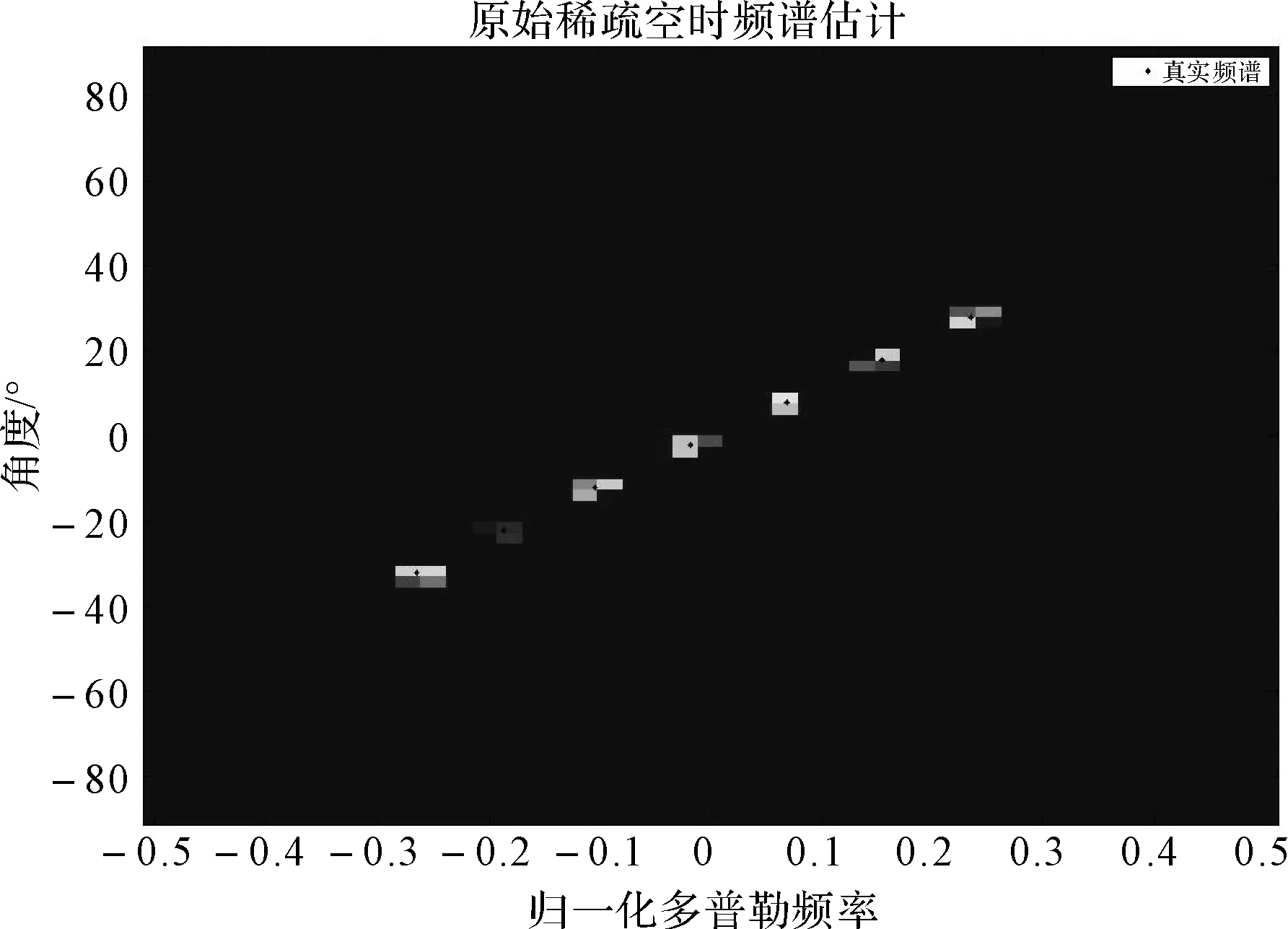
图2　基矩阵校正结果示意(七个杂波散射源)

同时,我们展示了最终滤波输出的改善因子对比图,该图是在主波束方向沿着归一化多普勒频率得到的。从图中可以看出,TLS-LASSO方法的改善因子效果明显好于常规稀疏恢复方法,主杂波区凹口宽度更窄,意味着能够获得更好的杂波抑制性能和更好的慢速小目标检测性能。

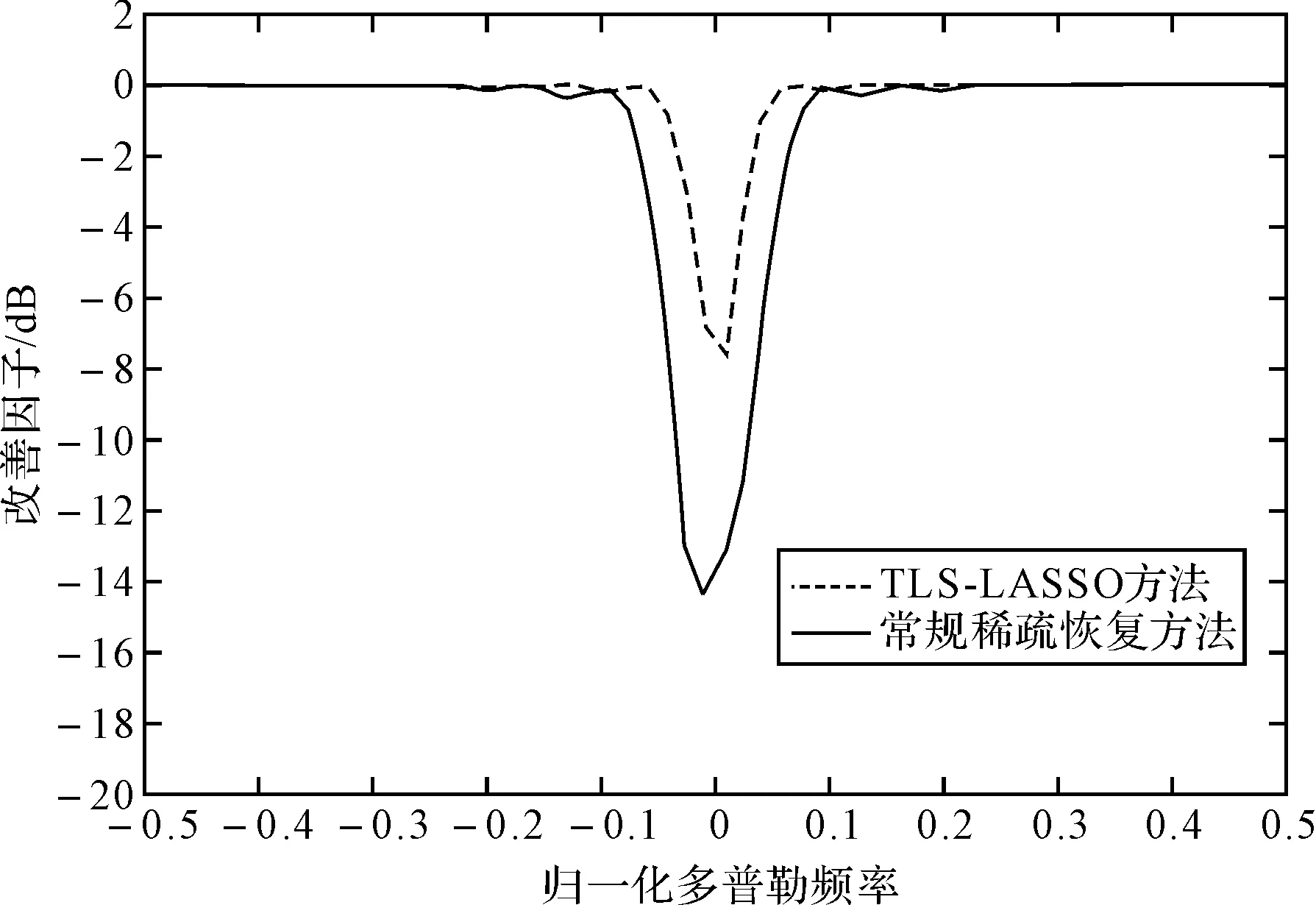
图3　改善因子对比图

以上实验结果充分说明了TLS-LASSO方法在校正基矩阵导引矢量空时频率中的有效性,可以通过自适应校正得到对空时频率误差的估计,实现对基矩阵空时频率的校正,从而获得更加准确的稀疏空时谱估计,获得更好的杂波抑制性能。

5结语

本文研究了机载预警雷达杂波抑制的重要方法——基于稀疏恢复的STAP方法中,基矩阵空时频率与真实杂波源不匹配的off-grid问题。通过建立参数化的空时频率误差模型以及合理的近似,将空时频率误差从非线性项中提取出来,成为基矩阵的加性误差项,进而建立了基于总体最小二乘和稀疏约束的优化问题,通过迭代求解该优化问题,同时获得了对稀疏空时谱和基矩阵空时频率误差的估计,从而实现了对基矩阵空时频率误差的校正。仿真实验表明,该方法能够较好估计空时频率误差,实现基矩阵校正,获得更加精确的稀疏空时谱估计,有效提高了杂波抑制性能。

6附录

式(13)～式(14)的推导

exp(j2πm(fd+Δfd))

=exp(j2πmfd)exp(j2πmΔfd)

=exp(j2πmfd)[cos(2πmΔfd)+jsin(2πmΔfd)]

≈exp(j2πmfd)(1+j2πmΔfd)

(27)

在上述推导中使用了Δfd→0这一假设,从而有cos(2πmΔfd)→0和sin(2πmΔfd)≈2πmΔfd。

(28)

上述推导中使用了Δθ←0这一假设,同前可得相应的近似。

参 考 文 献

[1] 陆军,郦能敬,曹晨.预警机系统导论[M].北京:国防工业出版社,2011.

CHAO Jun, LI Nengjing, CHAO Chen. Introduction to Airborne Early Warning System[M]. Beijing: National Defend Industry Press,2011.

[2] Klemm, Richard. Principles of space-time adaptive processing[J]. No. 159. IET,2002,159:15-19.

[3] Sun, Ke, et al. A novel STAP algorithm using sparse recovery technique[J]. Geoscience and Remote Sensing Symposium, 2009 IEEE International, IGARSS 2009,2009,5:29-35.

[4] Manolakis, Dimitris G, et al. Statistical and adaptive signal processing: spectral estimation, signal modeling, adaptive filtering, and array processing[M]. Norwood: Artech House,2005:13-18.

[5] Gabriel, William F. Adaptive processing array systems[J]. Proceedings of the IEEE,1992,80(1):152-162.

[6] 保铮,廖桂生,吴仁彪,等.相控阵机载雷达杂波抑制的时-空二维自适应滤波[J].电子学报,1993,21(9):1-7.

BAO Zhen, MIAO Guisheng, WU Renbiao, et al. Space-time adaptive filtering of clutter suppression for phased array aireborne radar[J]. Electronic Journal,1993,21(9):1-7.

[7] 王永良,彭应宁.空时自适应信号处理[M].北京:清华大学出版社,2000:50-52.

WANG Yongliang, PENG Yingning. Space-time adaptive signal processing[M]. Beijing: Tsinghua University Press,2000:50-52.

[8] Baraniuk, Richard G. Compressive sensing[J]. IEEE Signal Processing Magazine,2007,24(4):17-22.

[9] Ma Zeqiang, Yimin Liu, Huadong Meng, et al. Jointly sparse recovery of multiple snapshots in STAP[C]//Radar Conference(RADAR), 2013 IEEE: 1-4.

[10] Ma Zeqiang, Yimin Liu, Huadong Meng, et al. Sparse recovery-based space-time adaptive processing with array error self-calibration[J]. In Radar Conference(RADAR), 2014 IEEE:5-10.

[11] 马泽强,王希勤,刘一民,等.基于稀疏恢复的空时二维自适应处理技术研究现状[J].雷达学报,2010,10:23-26.

MA Zeqiang, WANG Xiqin, LIU Yimin, et al. An overview on sparse recovery-based STAP[J]. Radar Journal,2010,10:23-26.

[12] Tang, Gongguo, Badri Narayan Bhaskar, et al. Compressive sensing off the grid[J]. In Communication, Control, and Computing(Allerton), 2012 50th Annual Allerton Conference on IEEE,2012:778-785.

[13] Chi Yuejie, Louis L. Scharf, Ali Pezeshki, et al. Sensitivity to basis mismatch in compressed sensing[J]. Signal Processing, IEEE Transactions on 59,2011(5):2182-2195.

[14] Tibshirani, Robert. Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society, 1996, Series B(Methodological):267-288.

[15] Zhu Hao, Georgios B. Giannakis, Geert Leus. Weighted and structured sparse total least-squares for perturbed compressive sampling[C]//Speech and Signal Processing(ICASSP), 2011 IEEE International Conference on, 2011, IEEE,2011:3792-3795.

Basis Matrix Adaptive Correction of TLS-LASSO Algorithm Based on Sparse STAP

WANG Yali1JIA Hongjin2

(1. No. 91404 Troops of PLA, Qinhuangdao066001)(2. No. 91336 Troops of PLA, Qinhuangdao066001)

AbstractThe STAP algorithm of AEW radar clutter suppression required for stable snapshots too much, in the actual environment, it is difficult to get enough training samples for the scattering property of ground objects, through the introduction of sparse recovery can greatly reduce the required number of snapshots of clutter estimation. However, in the process of estimating the clutter space-time spectrum of the sparse recovery, there is not match phenomenon between the space-time frequency of the basis matrix and the real space-time frequency of the clutter, that is the off-grid problem. Off-grid severely affects the performance of sparse recovery space-time spectrum. In this paper, a basis matrix adaptive correction method based on TLS-LASSO is proposed for space-time frequency, it can solve the problem of off-grid. In the algorithm, the space-time frequency of each vector in the basis matrix is adaptively corrected while the space-time spectrum of sparse space is estimated, to find the base vector with the true position of the clutter, then obtain the corresponding sparse space-time spectrum, to avoid the problem of sparse recovery performance caused by off-grid. The simulation experiments show that the proposed algorithm has better recovery performance.

Key Wordsairborne early warning radar, space-time two-dimensional adaptive processing, sparse recovery, off-grid, basis matrix adaptive correction, space-time spectrum estimation

收稿日期:2015年12月18日,修回日期:2016年1月19日

作者简介:王亚莉,女,硕士,高级工程师,研究方向:雷达试验总体。贾宏进,男,博士,高级工程师,研究方向:电子对抗仿真。

中图分类号TN958.92

DOI:10.3969/j.issn.1672-9722.2016.06.008