混合流水车间调度问题的IPSO算法

李　解　任魏翔　秦永彬

(贵州大学计算机科学与技术学院　贵阳　550025)

混合流水车间调度问题的IPSO算法

李解任魏翔秦永彬

(贵州大学计算机科学与技术学院贵阳550025)

摘要混合流水车间调度问题又称柔性流水车间调度问题,广泛存在于现代工业之中。它是对传统流水车间的扩展。其中,每道工序可能有多台机器负责处理。针对混合流水车间调度问题,论文以最小化最大完成时间为目标建立整数规划模型,将经典粒子群优化算法进行改进,并同教与学算法(Teaching-Learning Based Optimation,TLBO)相结合,提出了一种用于解决该问题的改进的粒子群算法(Improved Particle Swam Optical Algorithm,IPSO)。算法在产生初始种群的过程中,首先将原问题转化为一系列置换流水车间调度问题,并求得其解。之后,将得到的解作为初始种群的一部分。由于现有的粒子群算法具有易收敛于局部最优解的缺点。因此为防止算法收敛于局部最优解,引入变异操作。此外,在粒子群优化算法的基础上引入适用于求解混合流水车间的TLBO算法的老师阶段和学生阶段。设计正交试验对算法参数设置进行分析,并确定了较优的参数组合。通过基于算例的仿真实验,并与现有的解决混合流水车间调度问题的算法进行比较,验证所提出IPSO算法是有效的。

关键词流水车间调度; 粒子群算法; TLBO; IPSO; 最大完成时间

Class NumberTP312

1引言

混合流水车间调度问题是置换流水车间调度问题的扩展。混合流水车间由一系列生产阶段组成。其中,至少一个阶段包括多台并行机器。每个待处理任务包含相同的工序,并且每个任务工序顺序相同。任务的每道工序只由相应生产阶段中的一台机器处理。混合流水车间调度问题作为置换流水车间调度问题的扩展,其研究成果不仅应用于电子[1]、汽车[2]等制造行业,而且在实时图像分析技术[3]等计算机领域的前沿发挥了重要作用。由于具有两个生产阶段,第一个生产阶段机器数为1,第二个生产阶段机器数为2的混合流水车间调度问题已是强NP-hard[4]。因此,在问题规模增加的情况下,合理的时间内已无法精确求得条件更为复杂的混合流水车间调度问题的最优解。Wittrock[5]首次提出以最小化最大完成时间为目标且生产阶段数大于3的混合流水车间调度问题,并为该问题提出了一种分支定界算法。为更加有效地得到该类问题的近似解,并且使其更接近于最优解蚁群算法[6]、模拟退火算法[7]、禁忌搜索[8]等智能优化算法及其混合算法[9～10]被用于混合流水车间调度问题。其中,蚁群算法通过模拟蚁群搜索食物求解调度问题。该算法的并行性高且不易收敛于局部最优解。但是由于蚁群算法相对复杂。因此,该算法的收敛速度慢。模拟退火算法来源于固体有高温降温至常温过程中分子由无序状态到基态的物理原理。该算法能够搜索到较接近于最优解的近似解,并且易于实现。但是模拟退火算法对参数的选择较敏感,且对问题的解搜索速度慢。禁忌搜索算法是一种模拟人类思考过程中的记忆功能避免对问题的一些解的迂回搜索的算法。该算法的运行结果对初始解具有较强的依赖性。与以上智能优化算法不同的是,粒子群算法具有简洁性、易实现以及快速收敛性等优点。但是该算法在已陷入局部最优,并且其理论基础不完善。因此,该算法仍存在大量的研究空间。

粒子群优化(Particle Swarm Optimization,PSO)算法最早是为解决连续非线性函数而提出的一种智能优化算法[11]。该算法通过模拟鸟群等动物群体的迁移活动来解决各种优化问题。现阶段对PSO算法的改进主要集中在与其他算法相结合、改进编码方式,利用其他算法的解作为初始种群的一部分等方面。

教与学优化算法(Teaching and Learning Based Optimation,TLBO)来源于学校教学过程中老师对学生的教与学过程以及学生之间的相互学习过程。在教学过程中,老师通过教学提升学生的知识水平。同时,学生之间能够通过相互学习来提高自身的知识水平。教与学算法首先在文献[12]中被提出,并且成功地应用于求解优化问题。教与学算法被提出以来已经成功地运用于各种优化问题之中。

本文针对混合流水车间调度问题,提出一种新的初始种群产生方法,并引入变异操作,并引入教与学优化算法中适用于求解混合流水车间调度问题的老师阶段和学生阶段,从而提出一种改进的粒子群优化算法(Improved Particle Swam Optimization Algorithm,IPSO)。通过仿真实验验证所提出算法能够在合理的时间内得到混合流水车间调度问题较优的近似解。

2问题描述

具有m(m≥2)阶段混合流水车间调度问题描述如下:生产系统所包括生产阶段数为m(m≥2),各生产阶段由多台具有相同加工功能且性能不一定相同的并行机器组成。n个待加工工件在生产系统中按照相同的工序顺序进行加工,并且不同工件在相同机器上的处理时间相互独立。工件的第r(r=1,2,…,m)道工序只能由第r个生产阶段的并行机器中的一台机器处理。问题的优化目标:对待处理工件排序并为各工件分配机器,使得生产系统处理完成所有工件的最大完成时间最小。该调度问题以文献[13]所提出的三元组α|β|γ方式可以表示为F(k1,k2,…,km)‖Cmax。其中,第一部分F(k1,k2,…,km)表明该问题的机器环境是具有r个阶段,每个阶段具有ki(i=1,2,…,m)台并行机器的混合流水车间;第二部分描述与任务相关的特征和约束,此处为空表示没有相应的约束限制;第三部分Cmax描述问题的优化目标为最小化最大完成时间。

基于以上描述,问题目标为:确定负责处理所有待处理任务的各道工序的机器以及各台机器处理任务的顺序,即调度S,使得最大完成时间Cmax最小。由于每个工件工序顺序相同,并且同一生产阶段上的机器性能不一定相同。所以,Cmax为调度S中所有任务在第m个阶段的完成时间的最大值,即maxCjm(j=1,2,…,n)。

3数学模型

假设生产系统需要处理n个工件,各工件的处理包括顺序相同的m道工序。生产系统中第r个生产阶段负责处理工件的第r道工序,并且该生产阶段上机器数为kr。工件的每道工序由相应生产阶段上的一台机器进行处理。

基于以上假设、问题描述以及相关符号说明,可以将F(k1,k2,…,km)‖Cmax混合流水车间调度问题转换为如下整数规划问题:

min max{Cjm}

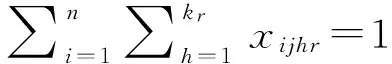
(1)

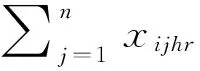
(2)

(3)

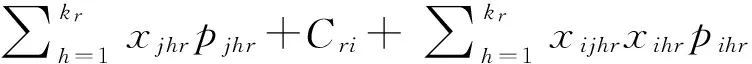
(4)

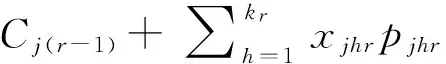
(5)

xijhr,xi0hr,x0jhr,xjhr∈{0,1}

(6)

其中,i=1,2,…,n;j=1,2,…,n;h=1,…,kr;r=1,2,…,m。

整数规划问题的目标为min max{Cjm},即最小化最大完成时间。

约束(1)确保每个任务的每道工序只能由一台机器进行处理,约束(2)确保每台机器同一时刻只能处理一个工件,约束(3)确保任何一台机器上处理的每一个任务最多只能有一个前趋任务、约束(4)用于计算任务的完成时间、约束(5)确保每个工件的工序顺序相同;约束(6)为4个指示变量,每个变量取值涵义如下:

4IPSO算法

粒子群优化算法模拟捕食行为的一种进化算法。其在执行过程中保存了若干个可行解,每个可行解称为一个粒子,若干个粒子构成一个种群。算法在执行的过程中,各粒子通过不断调整各自的速度和位置信息向问题的最优解移动。为防止粒子群算法在执行过程中陷入局部最优解,本文在标准粒子群算法的基础上引入变异操作。

4.1粒子的编码

4.2种群初始化

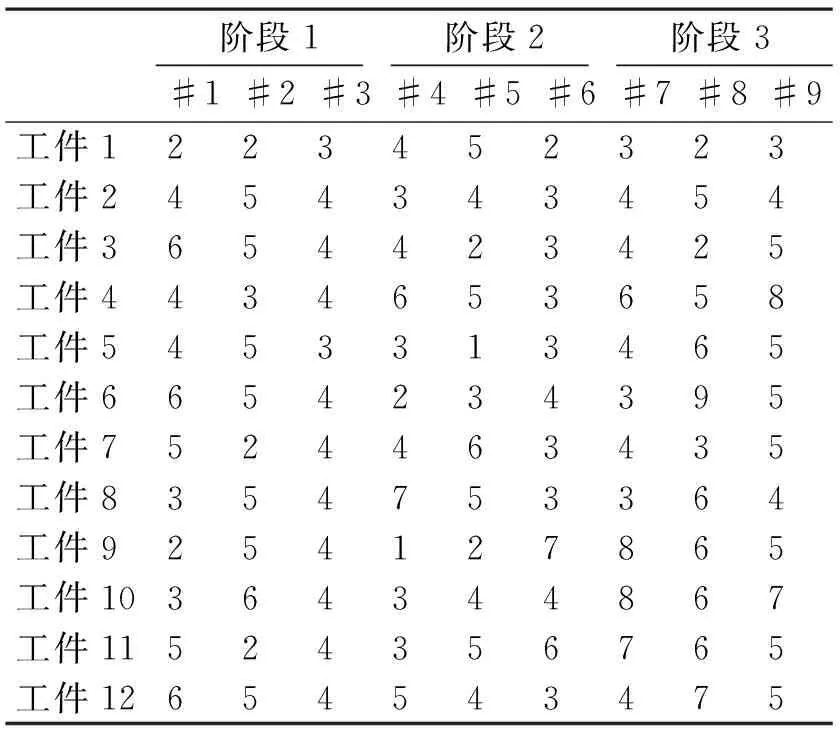
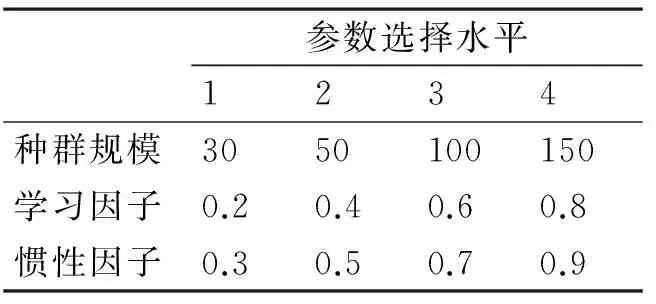
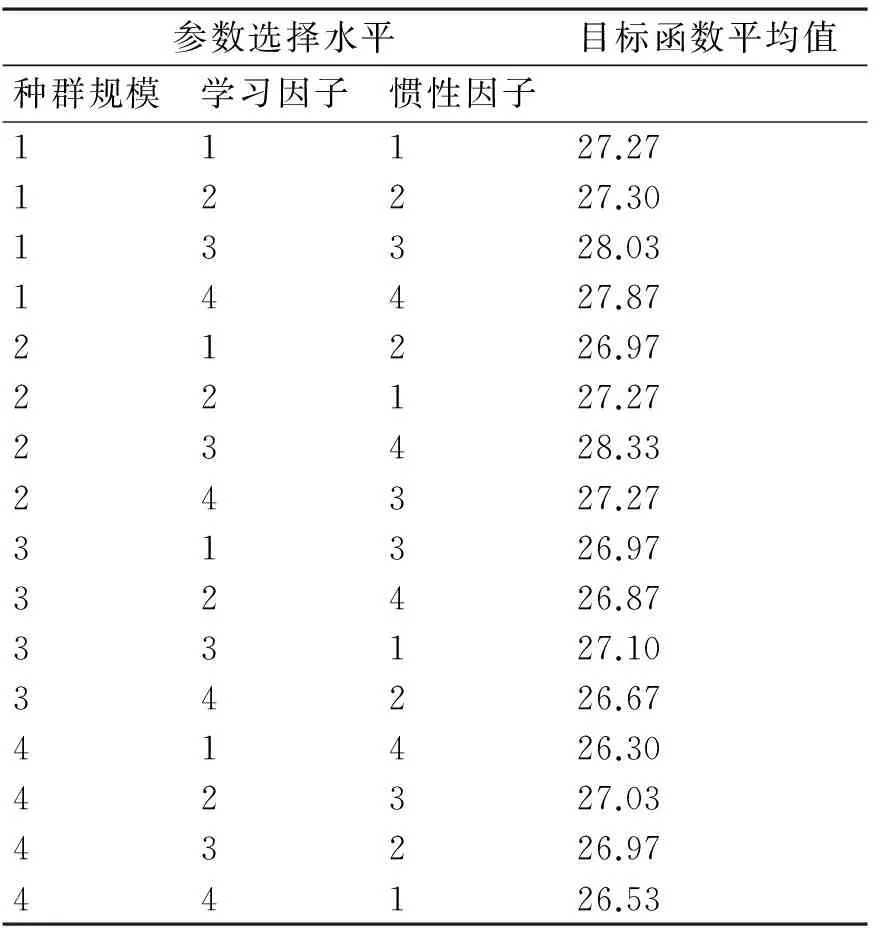
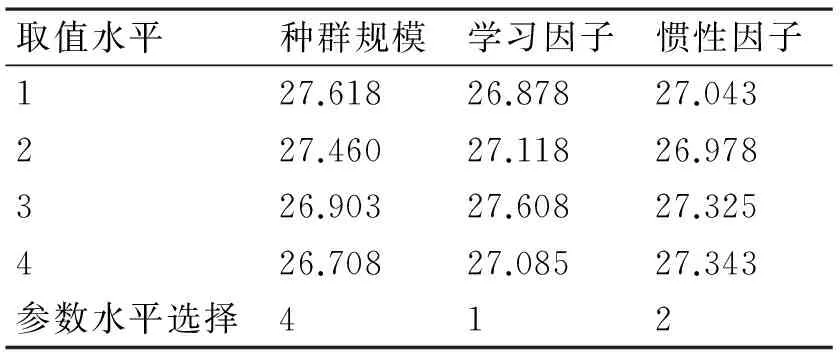
在算法的第一次迭代之前,产生初始种群。本文所设计算法的初始种群由三部分组成。假设算种群规模为popsize。初始种群的第一部分为原问题转化而成的Fm|(perm)|Cmax调度问题的解。第二部分为将原问题转换为m-1个F2|(perm)|Cmax问题的解。第三部分的初始解以均匀分布随机生成popsize-m个解。

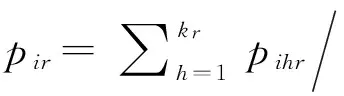
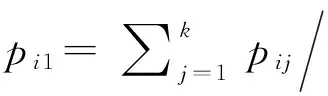
初始种群的剩余部分以均匀分布随机生成。

4.3粒子速度和位置的更新

粒子群算法在执行过程中,各个粒子通过各自的局部最优解以及全局最优解更新自身的速度和位置信息,向问题的最优解的位置靠近。传统的粒子群算法中粒子的位置和速度更新公式如下

v(t+1)=ω×v(t)+c1×r1×(p(t)-x(t))

+c2×r2×(g(t)-x(t))x(t+1)

=x(t)+v(t+1)

其中,ω为惯性因子;v(t+1)为该粒子在算法的第t+1次迭代的速度;x(t+1)为粒子在算法的第t+1次的位置;c1为局部最优解对速度更新影响的权重;c2为全局最优解对速度更新影响的权重;r1、r2为0～1之间的随机数;p(t)为粒子在算法的第t次迭代的局部最优解;g(t)为算法第t次迭代的全局最优解。

但是由于F(k1,k2,k3,…,km)‖Cmax问题解的采用矩阵方式进行编码,所以以上粒子速度和位置的更新方法已不适用。基于以上原因,本文采用另一种方式对粒子速度和位置进行更新。对粒子的速度随机地进行交换方式或者插入方式的更新。将各粒子与全局最优解或者局部最优解进行交叉操作来更新粒子的位置信息。

粒子以交换方式或者插入方式进行速度更新的具体过程如图1、图2所示:在当前解的矩阵中随机选取两行。粒子若以交换方式进行速度更新,则将随机选取的两行的内容进行交换。粒子若以插入方式进行更新,则将其中一行插入到另外一行之前。

图1　交换方式更新速度

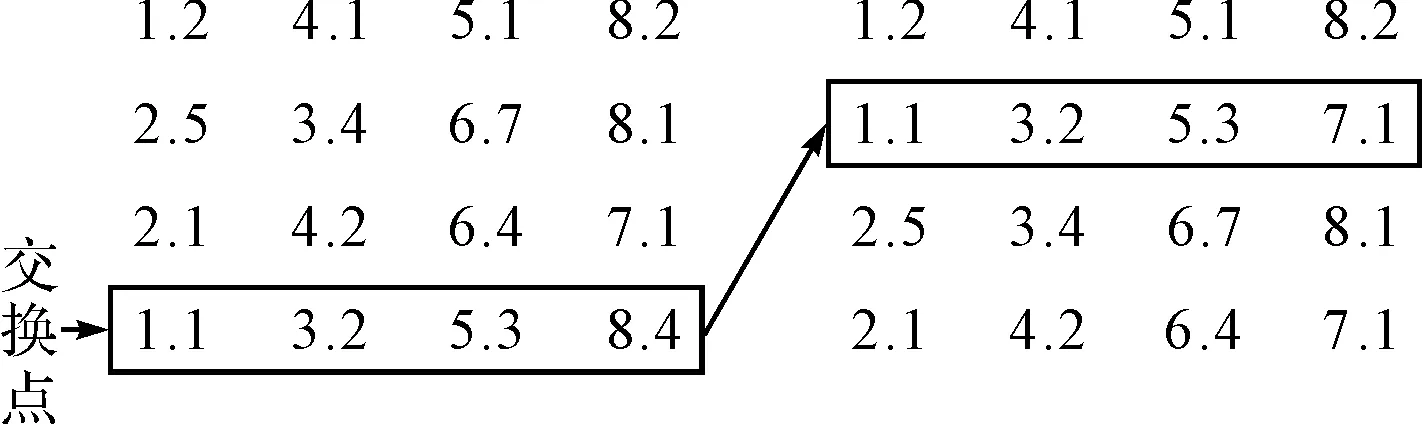
图2　插入方式更新速度

粒子以交叉操作进行位置更新的具体过程为:在当前解中随机选取两个交叉点i,j(1≤i

4.4变异

为防种群中粒子的多样性降低,从而造成算法的早熟收敛,对进入局部最优的粒子进行变异操作。本文算法首先判断在最近的若干次迭代中各个粒子的局部最优解是否发生变化。若存在局部最优解没有变化的粒子,则认为算法陷入局部最优解并对该粒子进行变异操作。

执行变异操作的粒子随机选择某一工件,并以均匀概率分布将负责处理该工件各道工序的机器改为生产系统中相应生产阶段的其他机器。

4.5老师阶段

教与学算法的老师阶段中,老师通过教授学生知识来提高学生的知识水平或者成绩,使学生的知识水平或成绩接近于老师的知识水平或成绩。算法在老师阶段的执行过程中如下:

1) 在粒子群中选择若干适应值最高的粒子作为老师,其他的粒子作为老师。

2) 被选为老师之外的每个粒子,随机选择一个老师,与其进行交叉操作。采用交换方式进行交叉操作。

3) 若交叉结果对应的适应值优于交叉之前的适应值,那么更新当前粒子为交叉所得的结果。

4.6学生阶段

该阶段的执行过程中,每个学生通过同学之间的相互学习来提高自身的知识水平或者成绩。算法在学生阶段的执行过程:每个学生选择高于其适应值的学生进行交叉操作,并更新当前学生粒子为交叉结果。

4.7终止条件

当算法迭代次数达到指定值后,算法停止运算,并输出结果。

4.8IPSO算法的具体步骤

IPSO算法:

Input:P,PT//PT为各个生产阶段包含的机器的数量

Output:S,Cmax

Begin:

Step1初始化算法最大迭代次数eranum、惯性系数InertiaCoef、学习系数LearnCoef、种群规模popsize,目标值未改变的次数unchangedTimes等参数。

Step2产生粒子数量为popsize的初始种群。在3维矩阵Schedule中记录初始种群中每个粒子的编码矩阵。在矩阵ValForGB中记录种群的全局最优值,并用矩阵GB记录全局最优值对应的矩阵编码。在矩阵ValForPB中记录各粒子的局部最优值,并在矩阵PB中记录局部最优值对应的矩阵编码。

Step3如果算法迭代次数小于最大遗传代数eranum,则转Step4,否则,转Step7

Step4种群Schedule中每个粒子以概率InertiaCoef更新速度,以概率LearnCoef更新根据局部最优值ValForPB更新位置,或者根据全局最优值ValForGB更新位置信息。计算更新后各个粒子对应的目标函数值,并将计算结果存入矩阵ValForSchedule中。

Step5如果ValForSchedule中最小值小于ValForGB中的值,则更新ValForGB为ValForSchedule中的最小值,同时更新GB为ValForSchedule中的最小值对应的编码矩阵;否则,不更新GB和ValForGB。如果粒子更新后对应的目标函数值小于其局部最优值,则更新该粒子局部最优值ValForPB为当前粒子对应的目标函数值,同时更新PB为当前粒子对应的编码矩阵。

Step6在Schedule中选择对应ValForSchedule值最小的若干个粒子作为老师teacherSchedule。

Step7对于每个粒子,在teacherSchedule中随机选择一个粒子作为老师,并与其进行交叉操作。若交叉结果的适应值优于当前粒子的适应值,则更新当前粒子为交叉结果。

Step8对于每个粒子,随机选择种群中的另外一个适应值更高的粒子,并与其进行交叉操作。更新当前粒子为交叉操作所得的结果。

Step9计算各个粒子对应目标函数值连续未改变的算法迭代次数。若未改变的算法迭代次数超过unchangedTimes的值,则对该粒子进行变异操作;否则,不进行变异。转Step3。

Step10输出GB和ValForGB,算法结束运行。

End

5实验设计与结果

5.1实验设计

本文提出的算法在Matlab 2014环境下实现,并运行于在CPU为Inter Core 3.20GHz的计算机。为确定算法中种群规模、学习因子、惯性因子等参数的取值,利用文献[14]中实例的数据设计因子数为3,因子取值水平数为4,参数组合数为16,即规模为L16(43)的正交试验。正交试验中各个任务的加工时间如表1所示。其中每个参数取值即正交试验的因子取值包括三个水平,如表2所示。每种参数组合各进行30次试验,并计算目标函数的平均值。算法最大迭代次数为1000次。正交试验的结果如表3所示。

表1　正交试验中各个任务的加工时间

表2　算法参数取值水平

表3　正交试验具体结果

表4　各参数取值水平的影响

由正交试验的具体结果可得出种群规模、学习因子、惯性因子这三个参数的不同取值水平对算法的影响,如表4所示。通过观察各参数不同取值水平对目标值的影响,发现当种群规模、学习因子、惯性因子取值水平分别为150、0.2、0.5时,所对应的目标函数值最小。因此,设定算法的种群规模为150,学习因子为0.2,惯性因子为0.5。

本文选取文献[15]和文献[16]的不同规模的测试数据验证本文提出算法的有效性。第1组实验数据包括12个任务,4个生产阶段。其中,每个生产阶段分别包括3台、3台、2台、2台并行机器。各个任务在每道工序中的每台机器上的加工时间如表5所示。第2组实验数据的任务数为12,生产阶段数为3,机器数为8,。其中第1个生产阶段包括3台机器,第2个生产阶段的包括3台机器,第三个生产阶段包括2台机器。各个任务在每台机器上处理所需时间如表6所示。

表5　第1组实验任务处理时间数据

表6　第2组实验任务处理时间数据

5.2实验结果与分析

利用所提出算法求解分别第1组实验实例和第2组实验实例各10次,实验结果如表7和表8所示。

表7　第1组实验结果

表8　第2组实验结果比较

本文提出算法10次运算第1组实验实例的最优解为302,最差解为320。而文献[15]所提出方法所得最优结果为347。基于以上分析,本文提出算法优于文献[15]提出的方法。

通过对表8中数据的分析可得,文献[16]的算法最优解为14,本文提出算法的最优解为12。并且本文所提算法每次运算结果均优于文献[16]中算法的结果。因此,所提出IPSO算法优于文献[16]所提出的方法。

6结语

本文在研究混合流水车间调度问题的基础上,将粒子群优化算法和教育学优化算法相结合,提出了用于求解该类问题的IPSO算法。初始解产生过程中,将原问题转换为Fm|(perm)|Cmax以及多个F2|(perm)|Cmax流水车间调度问题,并将所转换问题的解作为初始解的一部分。通过正交试验设置合适的算法参数。设计仿真实验并与已有的文献中计算结果进行比较。仿真实验的结果表明,本文所提出的IPSO算法能求得混合流水车间相对较优的近似解。

下一步的研究方向:改进所提出的算法或提出更为高效的算法用于求解具有随机故障的混合流水车间调度问题。

参 考 文 献

[1] Kurz M E, Askin R G. Scheduling flexible flow lines with sequence-dependent setup times[J]. European Journal of Operational Research,2004,159(1):66-82.

[2] Wilson J M. Henry Ford vs. assembly line balancing[J]. International Journal of Production Research,2014,52(3):757-765.

[3] Ercan M F, Fung Y F. Real-time image interpretation on a multi-layer architecture[C]//TENCON 99. Proceedings of the IEEE Region 10 Conference. IEEE,1999,2:1303-1306.

[4] Hoogeveen J A, Lenstra J K, Veltman B. Preemptive scheduling in a two-stage multiprocessor flow shop is NP-hard[J]. European Journal of Operational Research,1996,89(1):172-175.

[5] Wittrock R J. Scheduling algorithms for flexible flow lines[J]. IBM Journal of Research and Development,1985,29(4):401-412.

[6] Sioud A, Gagné C, Gravel M. An ant colony optimization for solving a hybrid flexible flowshop[C]//Proceedings of the 2014 conference companion on Genetic and evolutionary computation companion. ACM,2014:17-18.

[7] Mirsanei H S, Zandieh M, Moayed M J, et al. A simulated annealing algorithm approach to hybrid flow shop scheduling with sequence-dependent setup times[J]. Journal of Intelligent Manufacturing,2011,22(6):965-978.

[8] Shahvari O, Salmasi N, Logendran R, et al. An efficient tabu search algorithm for flexible flow shop sequence-dependent group scheduling problems[J]. International Journal of Production Research,2012,50(15):4237-4254.

[9] Niu Q, Zhou T, Ma S. A Quantum-Inspired Immune Algorithm for Hybrid Flow Shop with Makespan Criterion[J]. J. UCS,2009,15(4):765-785.

[10] Janiak A, Kozan E, Lichtenstein M, et al. Metaheuristic approaches to the hybrid flow shop scheduling problem with a cost-related criterion[J]. International Journal of Production Economics,2007,105(2):407-424.

[11] Eberhart R C, Kennedy J. A new optimizer using particle swarm theory[C]//Proceedings of the sixth international symposium on micro machine and human science,1995,1:39-43.

[12] Rao R V, Savsani V J, Vakharia D P. Teaching-learning-based optimization: a novel method for constrained mechanical design optimization problems[J]. Computer-Aided Design,2011,43(3):303-315.

[13] Graham R L, Lawler E L, Lenstra J K, et al. Optimization and approximation in deterministic sequencing and scheduling: a survey[J]. Annals of Discrete Mathematics,1979,5:287-326.

[14] 周辉仁,唐万生,魏颖辉.柔性Flow Shop调度的遗传算法优化[J].计算机工程与应用,2009,45(30):224-226.

ZHOU Renhui, TANG Wansheng, WEI Yinghui. Genetic algorithm optimization of flexible Flow Shop scheduling[J]. Computer Engineering and Applications,2009,45(30):224-226.

[15] 崔建双,李铁克,张文新.混合流水车间调度模型及其遗传算法[J].北京科技大学学报,2005,27(5):623-626.

CUI Jianshuang, LI Tieke, ZHANG Wenxin. Hybrid flow shop scheduling model and genetic algorithm[J]. Journal of University of Science and Technology Beijing,2005,27(5):623-626.

[16] 董婷婷.基于遗传算法的混合流水车间调度问题研究[D].阜新:辽宁工程技术大学,2008.DONG Tingting. The Study Based on the Genetic Algorithm of Hybrid Flow Shop Scheduling Problem[D]. Fuxin: Liaoning Technical University,2008.

Improved Particle Swam Optimization Algorithm for Hybrid Flow Shop Scheduling

LI JieREN WeixiangQIN Yongbin

(College of Computer Science and Technology, Guizhou University, Guiyang550025)

AbstractFor the hybrid flow shop scheduling problem which aims to minimize makespan, an integer program model is established. The improved particle swarm optimization algorithm with a new method of generating initial population, which is based on the study of classic particle swarm optimization algorithm, is presented. The new method transforms the hybrid flow shop scheduling problem into m-machine permutation flow shop scheduling problem. Parts of initial solutions consist of the transformed scheduling problem solution. The teacher phase and student phase of TLBO for solving hybrid flow shop scheduling problem is introduced into the proposed algorithm. The phenomenon that the particle converging on local optimum is avoided by mutation operation. Suitable parameters are suggested by perpendicular experiments on influence of parameter setting. Simulation experiments and comparisons with existing algorithms show the presented algorithm is effective.

Key Wordsflow shop, particle swarm optimization, teaching-learning based optimization, improved particle swarm optical algorithm, makespan

收稿日期:2015年12月4日,修回日期:2016年1月19日

基金项目:国家自然科学基金(编号:61262006,61540050);贵州省重大应用基础研究项目(编号:黔科合JZ字[2014]2001);贵州省科技厅联合基金(编号:黔科合LH字[2014]7636号);贵州大学研究生创新基金(编号:研理工2015012)资助。

作者简介:李解,女,硕士,研究方向:算法设计与分析。任魏翔,男,硕士,研究方向:算法设计与分析。秦永彬,男,副教授,硕士生导师,研究方向:智慧计算与智能计算、大数据管理与应用等。

中图分类号TP312

DOI:10.3969/j.issn.1672-9722.2016.06.001