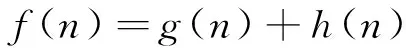裂缝区域优化随机扩展航路规划方法

何仁珂, 魏瑞轩, 张启瑞, 许卓凡, 周凯

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

裂缝区域优化随机扩展航路规划方法

何仁珂, 魏瑞轩, 张启瑞, 许卓凡, 周凯

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

摘要:针对密集障碍代价空间中存在的局部裂缝区域,基于采样的路径规划方法随机生成的节点无法进行有效扩展,形成可行路径的概率极低的问题,采用电势原理建立环境威胁模型,提出局部区域启发模式转换机制及节点一步检测方法。采用路径代价改进Transition-based RRT算法的节点选择机制,实现节点扩展的双启发。仿真结果表明,该算法能够有效地解决上述问题,其算法性能和路径生成优于同类算法。

关键词:航路规划; 快速扩展随机树; 裂缝问题

0引言

航路规划是保证移动机器人及无人飞行器等各类智能体安全飞行和执行任务的基础环节。随着这一领域研究的不断深入,对于航路规划问题的求解由简单约束条件向复杂约束条件延伸,由二维空间向高维空间拓展。这一趋势对传统航路规划方法提出了巨大的挑战,特别在解决密集障碍空间航路规划问题上,传统航路规划算法如拓扑图[1]、人工势场法[2]、栅格法[3]、智能优化算法[4-5]等在算法适用性和计算效率方面有诸多限制。以快速扩展随机树[6](Rapidly exploring Random Tree,RRT)算法为代表的基于采样的路径规划方法,在处理二维、多维空间的复杂约束规划问题方面有着广泛的应用[7];但由于该算法是建立在随机采样的基础上的,因此路径生成带有很大的随机性。为了更好地处理节点选择问题,更为复杂的代价地图被应用于解决路径优化问题[8-11]。Karaman等[12]证明了RRT算法得到最优解的概率为零。近年来,研究人员又提出了许多改进算法用于求解最优或渐近最优路径。Li等[13]利用A*算法的启发函数改进了RRT算法,但无法避免局部最小问题。Lee等[14]从控制节点原始生成的角度减小了算法的计算代价。文献[15-16]提出将改进的RRT方法应用于二维空间的动态环境。Leonard等[17]提出Transition-based RRT(T-RRT)算法,利用随机优化的方法引导节点向低代价空间扩展,其性能明显优于一般启发的RRT算法。随机生成的节点,无法保证有效扩展到高代价区域中存在的局部低代价裂缝区域,而在实际任务中,这一区域是缩短航路、执行纵深突防打击任务的重要“安全走廊”,有着极为重要的战场价值。Berenson等[18]提出Gradien T-RRT算法,采用局部梯度下降法引导节点穿越裂逢区域;但是梯度下降方向是单一的,在代价空间中解决该类问题时,结果并非均优于T-RRT算法。

本文运用电学中关于空间电场和电势分布原理构建了飞行威胁场,构成代价空间,提出了局部区域启发模式转换机制和一步检测方法。在局部区域扩展受限的情况下,采用A*算法启发引导节点对T-RRT算法在全局和局部进行双启发,实现路径节点在局部裂缝区域的有效扩展。

1基于电势原理构建飞行威胁场

传统的建模方法通常是以威胁或障碍的边界确定威胁半径,建立圆形或球形的威胁模型。由于威胁的影响与相对距离有密切联系,因此这种方法无法有效地描述与距离有关的威胁程度。本文利用电学中有关电荷激发形成电场原理[19]建立以威胁点、目标点为元素的威胁场,通过电势公式对电场强度和距离的关系表达,较好地表征了飞机逼近威胁的紧迫度,以此构建代价空间。

假设有n个点电荷q1,q2,…,qn,根据电势场叠加原理,在点P处激发形成的电势为:

(1)

式中：ri为P点与qi的距离。

电场强度为:

(2)

设qoi为第i个威胁,威胁均为正电荷,目标点qt为负电荷。引入目标点后,电势场变化为:

(3)

式中：rt为目标点与飞行器的距离。电场强度的大小取决取决于激发电场的电荷,与电场中的受力电荷无关。设飞行器为受力试探电荷,不影响电势分布,以此建立完整的代价空间。

2T-RRT算法

首先定义标准RRT变量。对于空间C,存在若干障碍区域。设Cfree为一非障碍的自由状态空间,Cfree∈C;Tk为一个具有K个节点的扩展树,x为Tk的节点,且Tk∈Cfree;qinit为起点,qgoal为终点;令qrand为非障碍区空间的一个随机采样点,即qrand∈Cfree;qnear为树中找到距离qrand最近的节点。设p,q∈Cfree,令d(p,q)为状态点的距离,则d(qnear,qrand)≤d(q,qrand)。在qrand与qnear两点直线间取qnew,qnew∈Cfree,并满足d(qnear,qnew)=ρ,其中ρ>0,为树生长的最小单位长度,称为步长。

T-RRT算法能较好地解决在多维代价空间寻找合适低代价路径的问题。其主要思想是利用RRT算法向全局扩展的优势,结合Monte Carlo优化和模拟退火的方法判断是否接受新的节点,形成类似于随机优化方法的转换检测(Transition Tests)的判断机制,在代价空间中运用最小机械功的思想计算出代价最小的路径。当新节点为低代价点,则加入扩展树中;若为高代价点,则根据Metropolis准则函数判断是否能加入,取决于函数中温度T的值:

(4)

T的取值随扩展失败的次数nfailmax而调整,拒绝次数越多,则温度值越高,接受的概率越小,排斥高代价点,较好地处理了路径节点寻优与扩展的关系。

3优化随机扩展算法

基于采样方式的T-RRT算法在选择路径节点上有很大随机性。虽然该算法从机械功的角度对所有节点选择进行概率检验,确保筛选出低代价节点;但对于在高代价区域中存在的局部低代价空间无法进行有效的节点搜索,树扩展的概率极低。从根本上来讲,基于采样的方法的随机性在该问题上存在固有缺陷,因此,本文提出利用A*算法在低代价点上的搜索优势来改进T-RRT算法在裂缝问题上的不足。A*算法并不依赖于基于采样的方法获得节点,节点生成不受裂缝区域限制。值得注意的是,对于复杂密集阻碍区域,尤其是局部低代价区域,如何有效地解决有启发与局部最小的矛盾是关键问题。这就需要合理地将Metropolis准则函数与A*算法启发函数结合起来,从而在有效引导节点穿越裂缝区域的同时,保证避免局部最小问题。

首先进行威胁环境建模,将威胁设为正电荷,目标点设为负电荷,飞行器为正的点电荷,构建空间C。扩展树Tk进行随机节点qrand的生成,然后进行碰撞检测,当节点出现在高电势区时,判定该节点位于威胁区域。当qrand∉Cfree时,计数器加1,否则进入转换检测,根据相邻节点的电势差选择符合条件的qnear节点;当d(qnear,qrand)≤d(q,qrand)时,以步长ρ取qnew。检测条件为:

(5)

式中:cparent为扩展出qnew的父节点的代价;(cparent-cnew)/dij为代价斜率。当cnew代价低于cparent时接受该节点,否则当rand(0,1)

当计数器达到门限值nfail>nfailmax时停止计数,进入局部启发模式。以相同步长ρ计算当前节点qparent与周围8个节点的相对代价值。估价函数为:

(6)

(7)

式中:g(n)为路径长度;h(n)为当前节点qparent与目标节点qgoal的欧氏距离;(xi,yi)为周围节点。

接下来进行节点扩展测试。如果h(qparent,qgoal)135°,以此为条件筛选节点。

4仿真试验及结果分析

建立局部复杂密集障碍区域飞行威胁场,将本文算法与RRT, T-RRT, Gradien T-RRT进行对比分析,以检验算法在复杂密集障碍环境以及裂缝区域的性能。仿真试验环境:软件Matlab 7.0;计算机配置:Windows XP操作系统、CPU为Inter Core i3、主频3.3 GHz。仿真条件:设定11处威胁点,威胁强度由电量大小确定,电量为+1 C和+2 C,目标点电量为-10 C;飞行器为元电荷,电量为+1 C。飞行威胁场大小为50 km×50 km,设K为1,ρ=1,ε0=1/(4π),α≥135°。试验结果如图1所示。

图1　各种算法路径规划结果Fig.1　Planning results of various algorithms

由图1可以看出,对于密集障碍区域,各算法均能找到从起点到目标点的路径。RRT算法的随机扩展具有未知搜索优势,几乎遍布全局;但并不能很好地扩展到裂缝区域,路径随机性强,没有考虑运动约束条件。T-RRT算法能根据代价大小在全局中选择合适的扩展节点,从而路径扩展有很好的指向性,当在威胁区域扩展失败时可退出重点选取节点,很好地避开威胁所在的高代价区域。Gradien T-RRT算法在密集障碍区域进行了有效地扩展试探,路径在梯度引导下有良好的方向性;但由于梯度方向的限制,在靠近威胁时梯度易受威胁势能的影响,没有成功通过裂缝区域。本文算法能很好地穿越裂缝区域,且路径扩展有很好的方向性,局部启发能有效引导节点通过密集障碍区域。

为了更加清晰地反映上述算法在计算时间和路径代价上的优劣,本文设置最大扩展失败次数nfailmax为10～80次,每一层级在相同的条件下进行10次试验,结果如图2所示。由于RRT算法不具有此项性能,故不进行比较。

图2　各种算法的计算时间和路径代价Fig.2　Computing time and path cost of various algorithms

由图2可以看出,在相同条件下,T-RRT算法的计算时间和路径代价最大,且计算时间随nfailmax的增加逐渐变大,而对其他两种算法的影响不大。这是由于在密集障碍区域,T-RRT算法选择低代价节点的难度增大,扩展温度不断升高,随着nfailmax的增加,在同一节点扩展次数增加,计算时间随之提高;路径代价下降是因为nfailmax增加,能够保证选择合适节点的概率增大,生成的路径代价降低。Gradien T-RRT和本文算法由于在节点扩展失败后进行了不同模式的节点增长机制,从而在根本上改变了随机扩展的节点生成方式,因此计算时间和路径代价受nfailmax影响较小。对于密集障碍区域生成的路径，本文算法在计算时间和代价方面优于其他两种方法。

5结束语

本文针对基于采样的路径规划方法在密集障碍区域裂缝问题上的不足,在建立新型威胁模型的基础上,提出用A*算法改进T-RRT算法,从而有效地解决了算法在高代价局部区域节点扩展困难的问题,较好地实现了复杂密集障碍“双启发式”引导。与传统威胁模型相比,该威胁模型能有效表征威胁与相对距离的关系,更具有应用价值。本文的不足在于“一步检测”时需进行两次节点筛选,在数据规模较大时影响计算速度。下一步将对路径规划实时性和计算效率方面进行改进。

参考文献：

[1]Israel L,Flores G,Salazar S,et al.Dubins path generation for a fixed wing UAV[C]//International Conference on Unmanned Aircraft Systems (ICUAS).Orlando:IEEE,2014:339-346.

[2]Tingbin C,Qisong Z.Robot motion planning based on improved artificial potential field[C]//2013 3rd International Conference on Computer Science and Network Technology (ICCSNT).Dalian:IEEE,2013:1208-1211.

[3]Robert J S,Peggy G I S,Clickstein,et al.Robust algorithm for algorithm for real-time route planning[J].IEEE Transaction on Aerospace and Electronic System,2000,36(3):869-878.

[4]Tuncer A,Yildirim M.Dynamic path planning of mobile robots with improved genetic algorithm[J].Computer Electrical Engineering,2012,38(6):1564-1572.

[5]Chaari I,Koubaa A,Bennaceur H,et al.SmartPATH:a hybrid ACO-GA algorithm for robot path planning[C]//2012 IEEE Congress on Evolutionary Computation (CEC).Brisbane:IEEE,2012:1-8.

[6]Lavalle S M,Kuffner J J.Randomized kinodynamic planning[J].International Journal of Robotics Research,2001,20(3):378-400.

[7]Erion P,Kostas E B,Brjan Y C,et al.Samplng-based roadmap of trees for parallel motion planning[J].IEEE Transactions on Robotics,2005,21(4):597-608.

[8]Urmson C,Simmons R.Approaches for heuristically biasing RRT growth[C]//Proceedings of the IEEE/RSJ International Conference on Intelligent Robotics and Systems (Volume:2).Las Vegas:IEEE,2003:1178-1183.

[9]Lee J,Pippin C,Balch T.Cost based planning with RRT in outdoor environment[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems.Nice:IEEE,2008:684-689.

[10]Ettlin A,Bleuler H.Rough-terrain robot motion planning based on obstacleness[C]//9th International Conference on Control,Automation,Robotics and Vision.Singapore:IEEE,2006:1-6.

[11]Xu Y,Choi J,Oh S.Mobile sensor network navigation using Gaussian processes with truncated observations[J].IEEE Transactions on Robotics,2011,27(6):1118-1131.

[12]Karaman S,Frazzoli E.Sampling-based algorithms for optimal motion planning[J].International Journal of Robotics Research,2011,30(7):846-894.

[13]Li J,Liu S,Zhang B.RRT-A*motion planning algorithm for non-holonomic mobile robot[C]//2014 Proceedings of the SICE Annual Conference.Sapporo:IEEE,2014:1833-1838.

[14]Lee D,Shim D H.Spline-RRT*based optimal path planning of terrain following flights for fixed-wing UAVs[C]//2014 11th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI 2014) Hilton.Kuala Lumpur:IEEE,2014:257-261.

[15]Svenstrup M,Bak T,Andersen H J.Trajectory planning for robots in dynamic human environments [C]//2010 IEEE/RSJ International Conference on Intelligent Robots and Systems.Taipei:IEEE,2010:4293-4298.

[16]Jaillet L,Hoffman J,Berg J,et al.EG-RRT:environment-guided random trees for kinodynamic motion planning with uncertainty and obstacles [C]//IEEE/RSJ International Conference on Intelligent Robots and Systems.San Francisco:IEEE,2011:2646-2652.

[17]Leonard J,Juan C,Thierry S. Sampling-based path planning on configuration-space costmaps[J].IEEE Transaction on Robotics,2010,26(4):635-646.

[18]Berenson D,Simeon T,Srinivasa S S.Addressing cost-space chasms in manipulation planning[C]//2011 International Conference on Robotics and Automation.Shanghai:IEEE,2011:4561-4568.

[19]马文蔚.物理学[M].第5版.北京:高等教育出版社,2006:149-186.

(编辑：李怡)

Addressing chasm in optimization rapidly exploring path planning

HE Ren-ke, WEI Rui-xuan, ZHANG Qi-rui, XU Zhuo-fan, ZHOU Kai

(Aeronautics and Astronautics Engineering College, AFEU, Xi’an 710038, China)

Abstract:Narrow low-cost regions called chasm exits in dense obstacle cost space; it is difficult for sampling-based methods to extend nodes in this area. This paper built model based on electric potential, proposed local heuristic mechanism and step detection method, improved Transition-based RRT algorithm by path cost function. The results show that the proposed method could effectively solve the problem mentioned above, its algorithm performance and path generation method are better than others.

Key words:path planning; rapidly exploring random tree; chasm problem

收稿日期:2015-09-07;

修订日期:2015-11-28; 网络出版时间:2016-02-29 16:37

基金项目:国家自然科学基金资助(61573373)；航空科学基金资助(20135896027)

作者简介:何仁珂(1993-)，男，河南信阳人，硕士研究生，主要研究方向为无人机自主控制。

中图分类号：V249.1

文献标识码：A

文章编号：1002-0853(2016)03-0026-04