基于脆性联系理论的客滚船航行风险辨识研究*

陈厚忠　赵尊荣　郭国平　徐元春

(武汉理工大学航运学院1)　武汉　430063)　(内河航运技术湖北省重点实验室2)　武汉　430000)

基于脆性联系理论的客滚船航行风险辨识研究*

陈厚忠1,2)赵尊荣1)郭国平1,2)徐元春1)

(武汉理工大学航运学院1)武汉430063)(内河航运技术湖北省重点实验室2)武汉430000)

摘要：构建以客滚船为核心的SHEV风险辨识模型，筛选出客渡船运输过程中的5类脆性因子；通过AHP多目标综合评价确定各子系统中各因子的权重，得到权重向量Ai；再结合集对分析的数学方法，对各脆性因子进行赋权，并求取脆性关联熵值及脆性联系熵，进而进行客滚船航行风险辨识模型的研究.最后以北海至洋浦航线为例，进行模型的示范应用.

关键词：安全；客滚船；脆性联系理论；脆性因子；脆性联系熵；风险辨识模型

0引言

跨海客渡船运输是一种特殊中短程海上运输方式.在经济发达地区的环渤海、东南沿海、琼州海峡等中短途水运中，客滚船具有较大的竞争优势.跨海客滚船运输“客货兼运”的特性决定了客滚船运营过程中存在的重大安全隐患.据统计，过去的近30年中，国内外共发生重大客滚船事故12起.交通运输部对跨海客渡船运输的安全高度重视，将“跨海客运渡轮班线运营安全风险防控与示范”作为2015年交通行业重大科研项目展开专项研究.在此基础上，文中开展客滚船航行风险的研究，并提出基于脆性联系理论的风险辨识模型.

1风险辨识模型的构建

1.1风险辨识模型中的相关定义

1.1.1复杂系统

复杂系统[1](complex system)是指具有相当数目的能够对局部信息做出反应的智能性、自适应性系统，是相对简单系统而言的.它一般具有一个比较大的不断变化的环境背景及多个存在非线性关联关系的子系统，且相互间存在能量、物质和信息的交换.复杂系统一般包括硬件部分H(系统要素集合)、软件部分S(系统要素的关系集合)及外部环境E(干扰条件)，可表达为：

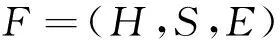
(1)

1.1.2脆性过程

复杂系统受外界物质、能量及信息的交换而产生由系统有序状态向无序状态发生不可逆转的变化，这个过程称之为脆性过程[2-3].脆性过程的类型分为：一对一、一对多和多对一，表现为单向性、多向性、传递性.

1.1.3脆性关联性

脆性过程产生的效果称为脆性关联性，包括：同一性、对立性及波动性，在数值上，可以依次定义为脆性同一熵Ha、脆性对立熵Hb、脆性波动熵Hc，脆性过程的整体效果可以用脆性联系熵HXY来表现.

1.1.4脆性因子

脆性因子是指产生脆性过程的脆性源.由于脆性因子的不稳定性，导致复杂系统集合运行过程中的不可确定性，这种不可确定性可能导致系统的崩溃.

1.2风险辨识模型的实现过程

1.2.1构建复杂系统集合F

文中将“客滚船航行”事件视为一个复杂系统集合F，航线条件、通航环境、船舶条件、人员条件及其他安全管理制度构成了集合F的硬件部分H和软件部分S，航线水域的通航环境、船舶性能、人员综合素质发生改变，安全管理制度缺陷等情况作为外部干扰条件E.理想情况下，在既定的航线上，客滚船航行事件将有序地进行下去，直到E对整个系统集合产生脆性作用为止.

1.2.2基于SHEL-SHEV模型的脆性因子的选取

文中从船舶的角度来对系统集合F的脆性过程进行分析，参考SHEL模型[4-5]并加以优化，得到如图1所示的“船舶(vessel)”所处特定系统界面的“SHEV模型”，通过分析主体客滚船航行过程中受到的其他要素影响，来辨识整个航线过程中系统集合F中的脆性源.

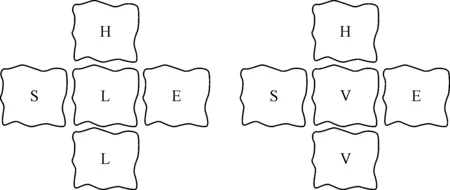
图1　SHEL-SHEV模型示意图

根据修正后的SHEV模型，可将影响因子分为船系统(V)、船-船系统(V-V)、船-硬件系统(V-H)、船-软件系统(V-S)、船-环境系统(V-E)5类，其中：

船系统(V)是指客滚船的因素.作为航线的主体，客滚船的因素直接影响着整个系统集合的有序性.客滚船因素主要包括：船舶结构特点、船舶现状(船龄、损坏程度)、船载设施设备、船舶操纵性能、船舶配员、船员适任情况、货物配积载、货物系固绑扎等；

船-船系统(V-V)是指客滚船受到的其他船舶影响，主要包括：船舶种类、船舶大小、船舶数量、交通流分布情况、通航密度、航线交叉情况、交通冲突点、渔船活动等；

船-硬件系统(V-H)是指客滚船航线船舶航行过程中的硬件设施及配套支持系统，主要包括：航道条件、锚地条件、桥区、渔业捕捞区、碍航物、转向点、导助航设施设备、辅助机械(拖轮等)等；

船-软件系统(V-S)是指影响客滚船安全航行的管理机制，主要包括：航行规则、主管部门的行政监管、公司安全管理、船舶安全管理、应急预案、船员日常演习、船岸通讯、岸基指导等；

船-环境系统(V-E)是指客滚船受到的自然环境影响，包括：风、波浪、水流、潮汐、雾及能见度、雷暴天气、夜航、热带气旋及台风等.

1.2.3基于集对分析理论和AHP的赋权过程

根据集对分析理论的思想[6]，针对“客滚船航行风险研究”问题对SHEV模型构成的集合X所包含的船系统(V)、船-船系统(V-V)、船-硬件系统(V-H)、船-软件系统(V-S)、船-环境系统(V-E)5类脆性因子进行集对分析，具体步骤为：

1) 根据风险研究的需要，进行安全状态的分级处理，包括一级状态(安全)、二级状态(一般)及三级状态(危险)，分别用三维向量来表示：(1,0,0)、(0,1,0)、(0,0,1).

2) 结合AHP层次分析的核心思想[7]，通过多层次综合评价分析，计算得到系统集合F中各子系统脆性因子的权重向量Ai.

3) 以三级状态(危险)为基准集合Y，根据步骤2)所计算的权重向量Ai对5类脆性因子就“客滚船航行风险研究”问题进行分析：若在权重向量Ai中所占权重较小，代表安全状态(一级状态)，则在集对分析中表现为对立性，记作(1,0,0)；若在权重向量Ai中所占权重较大，代表危险状态(三级状态)，则在集对分析中表现为同一性，记作(0,0,1)；若在权重向量Ai中所占权重一般(居中位置)，代表一般状态(二级状态)，则在集对分析中表现为波动性，记作(0,1,0).

脆性同一表示脆性因子可能会给客滚船航行带来较大风险；相反，脆性对立状态下，客滚船的航行安全是有保障的；脆性波动就是系统中的不确定成分，作用不稳定，通过加强警惕和付诸行之有效的防范措施，这部分脆性因子是可以转换为脆性对立的.

1.2.4脆性关联性的量化、定义及计算

根据集对分析理论的相关思想，对SHEV模型构成的集合X及基准集合Y进行相关定义[8].

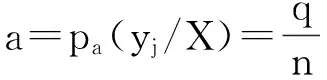
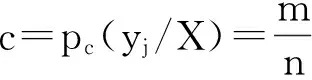
则有：

(2)

再定义脆性同一熵Ha为

(3)

脆性对立熵Hb为：

(4)

脆性波动熵Hc为：

(5)

式中：n为X系统中的脆性因子数；q为向量(0,0,1)的个数；p为向量(1,0,0,)的个数；m=n-q-p为向量(0,1,0)的个数.

脆性同一、脆性对立及脆性波动共同构成了集合X对集合Y的作用，这种作用效果可用两集合的脆性联系熵HXY来表示.

定义：

HXY=waHa+wbHb+wcHc

(6)

令：pa(yj/X)=a；pb(yj/X)=b；pc(yj/X)=c，则式中：wa，wb，wc分别为脆性同一、脆性对立、脆性波动的权系数.

脆性联系熵反映了系统集合脆性过程的综合作用效果，脆性联系熵越大，表示客滚船航行风险越大.

考虑到系统集合F中控制变量及状态变量的相互转换及权重系数的计算需要，本文拟采用客观赋权法——突变级数法[9-11]来进行计算.系统集合F中包含脆性同一熵、脆性对立熵及脆性波动熵三个控制变量及“客滚船航行安全”一个状态变量，采用燕尾突变级数法进行权重系数计算[12-18].

燕尾突变势函数：

(7)

分解形式的分解集方程：

a=-6x2,b=8x3,c=-3x4

(8)

为方便后续计算，采用归一法让状态变量a，b，c和控制变量x在[0,1]区间取值，结合计算得到的各子系统脆性同一熵Ha、脆性对立熵Hb和脆性波动熵Hc三个控制变量，将其代入可得：

(9)

式中：xa、xb、xc为三个控制变量Ha、Hb、Hc控制下的状态值，分别作为式(6)中的权系数，即wa、wb、wc.Ha、Hb、Hc的取值范围在0～1之间.

1.2.5结果分析

脆性联系熵值反映了子系统之间联系的不确定性程度，由于这种不确定性联系的存在使得一个子系统崩溃有可能最终导致整个系统的瘫痪.通过脆性关联性的量化及计算得到船系统(V)、船-船系统(V-V)、船-硬件系统(V-H)、船-软件系统(V-S)、船-环境系统(V-E)5个子系统的脆性联系熵HXYn(n=1,2,3,4,5).比较HXYn的大小，来确定各子系统的风险程度：系统集合F中，脆性联系熵越大，表示客滚船航行风险越大.确定各子系统的风险程度后，反过来通过权重向量Ai及各脆性因子的脆性关联性，对5类脆性因子进行单独分析，以实现客滚船航行风险的辨识.

1.2.6风险辨识模型

根据以上实现过程可得到如图2所示的风险辨识模型.

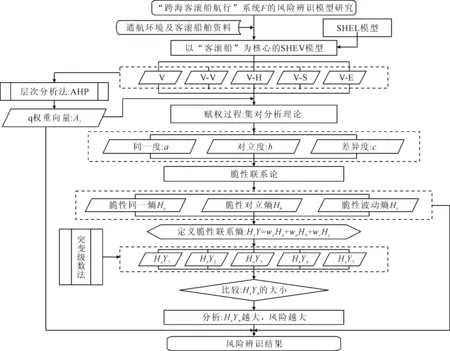
图2　风险辨识模型

2实例应用

2014年5月，北部湾旅游股份有限公司组织“北部湾3号”客滚船进行北海至洋浦航线试航，试航航线长100多nmile，途经广西沿海海域、涠洲岛及斜阳岛海域、洋浦外海及儋州湾海域.根据实地调研获取的通航环境及客滚船船舶资料，构建以北部湾3号客滚船为核心的SHEV模型，经2015年1月关联项目评审会上的专家打分及AHP方法计算，得到权重向量Ai.

A1=(船舶结构特点，船舶现状，船载设施设备，船舶操纵性能，船舶配员，船员适任情况，货物配积载，货物系固绑扎)=(0.141 1，0.054 5，0.054 5，0.054 5，0.054 5，0.054 5，0.293 2，0.293 2).

A2=(船舶种类，船舶大小，船舶数量，交通流分布情况，通航密度，航线交叉情况，交通冲突点，渔船干扰)=(0.068 5，0.030 6，0.068 5，0.068 5，0.191 0，0.191 0，0.191 0，0.191 0).

A3=(航道条件，锚地条件，桥区，渔业捕捞区，碍航物，转向点，导助航设施设备，辅助机械)=(0.043 0，0.268 2，0.043 0，0.268 2，0.111 5，0.111 5，0.043 0，0.111 5).

A4=(航行规则，行政监管，公司安全管理，船舶安全管理，应急预案，船员日常演习，船岸通讯，岸基指导)=(0.353 9，0.061 1，0.170 3，0.170 3，0.061 1，0.061 1，0.061 1，0.061 1).

A5=(风，热带气旋及台风，雾及能见度，雷暴天气，潮流，潮汐，波浪，夜航)=(0.260 2，0.100 5，0.100 5，0.100 5，0.038 8，0.038 8，0.260 2，0.100 5).

根据权重向量Ai，进行集对赋权，可得到脆性因子集对赋权及各子系统脆性关联度，见表1、表2.

计算脆性同一熵Ha、脆性对立熵Hb、脆性波动熵Hc及脆性联系熵HXY(见表3).

结合权重向量Ai、脆性联系熵HXY及各脆性因子的脆性关联性(见表1)，风险辨识结果分析如下.

根据1.2.3第3步的赋权规则可知，在各子系统内，脆性因子所占权重越大，对客滚船跨海航行安全影响越大；脆性同一的因子对客滚船跨海航行安全影响较大，脆性对立的因子对客滚船跨海航行安全影响较小，脆性波动的因子对客滚船跨海航行安全影响一般.

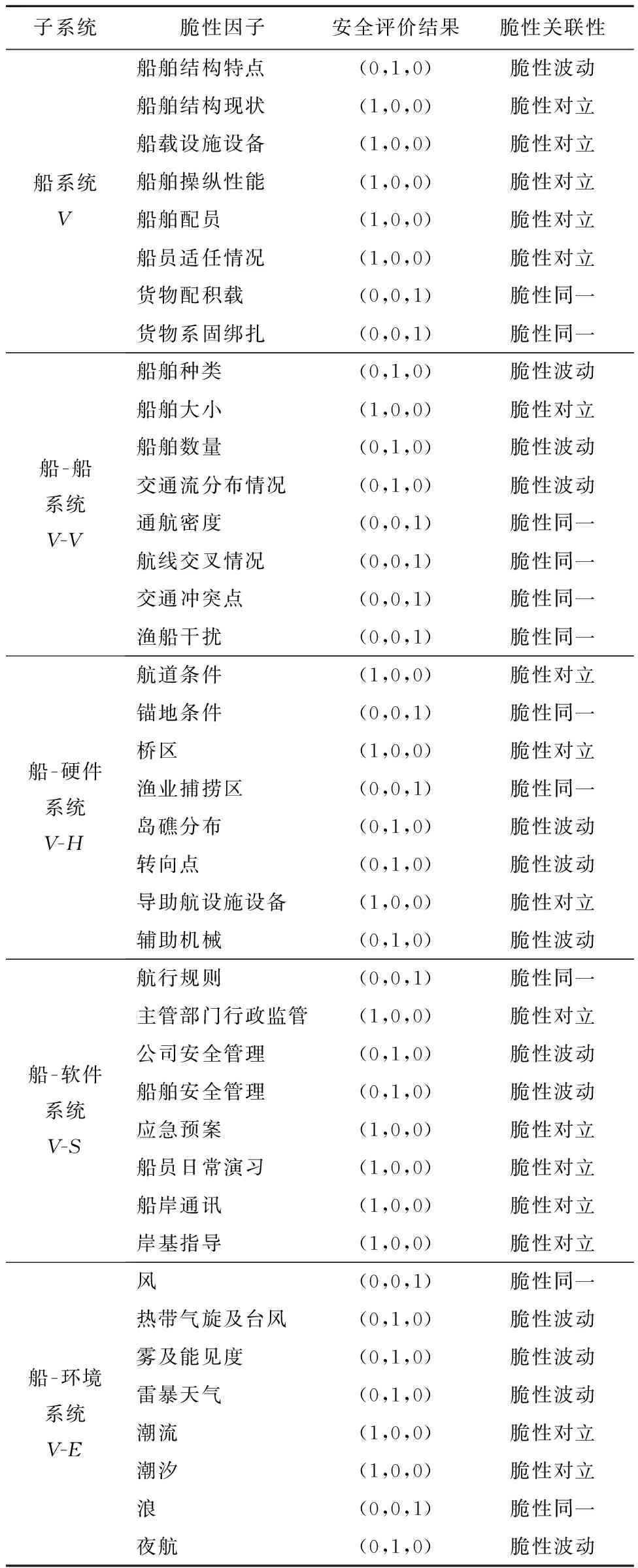
表1　脆性因子集对赋权表

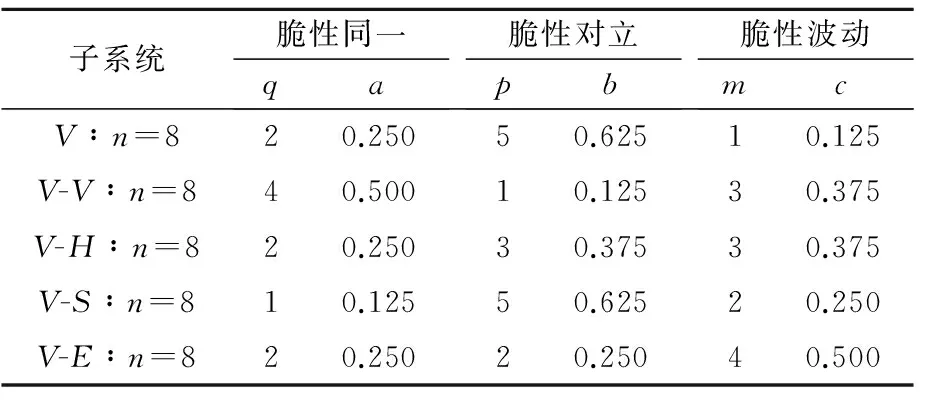
表2　各子系统脆性关联度

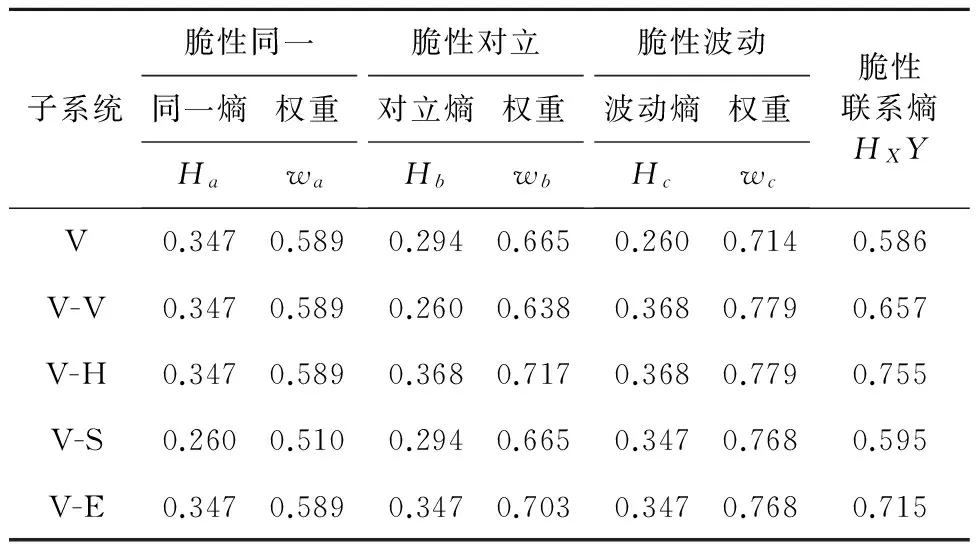
表3　各子系统脆性联系熵值及权重

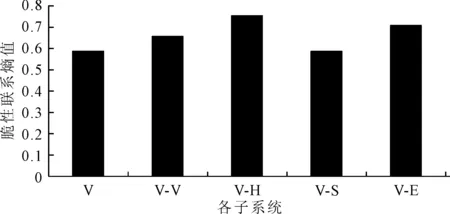
图3　5个子系统脆性联系熵对比图

系统集合F“北海至洋浦航线客滚船航行风险分析”的5个子系统共40项脆性因子中，船-硬件系统(V-H)、船-环境系统(V-E)的脆性联系熵较大，对客滚船安全航行产生较大的影响；船系统(V)、船-软件系统(V-S)的脆性联系熵较小，影响较小，基本能满足客滚船安全航行的要求；船-船系统(V-V)的脆性联系熵处中间位置，对客滚船航行产生一定的影响(见图3).具体地，对客滚船航行安全影响较大的因素主要包括：锚地条件，渔业捕捞及风、浪条件；其他例如航线交叉，交通流分布，交通冲突情况，热带气旋(台风)，雾及能见度等亦将对客滚船航行产生一定的影响；另外，也不能忽视客滚船本身结构特性、客滚船货物配积载及系固绑扎等方面因素给客滚船航行带来的威胁，同时做好加强公司和船舶安全管理工作.

3结 束 语

客滚船运输已成为现代交通运输系统中的重要一部分，开展客滚船航行风险辨识模型的研究，对于保障客滚船运输安全，促进现代交通运输系统进步具有重要的意义.文中基于脆性联系理论的相关思想，提出客滚船航行风险辨识模型，并选取北海至洋浦客滚船航线为例进行实际应用，具有一定的实用价值.在后续过程中，仍需对北海至洋浦航线进行进一步观察，以验证模型的准确性.

参 考 文 献

[1]李进,耿金花,赵洋,等.《复杂系统与复杂性科学》杂志载文统计与分析[J].青岛大学学报(工程技术版),2014,29(1):120-122.

[2]刘晓平,唐益明,郑利平.复杂系统与复杂系统仿真研究综述[J].系统仿真学报,2008,20(23):6303-6315.

[3]李丹.基于FAHP和脆性联系理论的交通安全系统脆性研究[D].南宁：广西大学，2013.

[4]刘丙泉.船舶人因事故预警管理研究[D].哈尔滨：哈尔滨工程大学，2009.

[5]刘刚.基于改进的SHEL模型的具体海事中人为失误分析[J].天津航海,2012(2):20-23.

[6]王菁.客滚运输人为因素风险评价与控制研究[D].大连：大连海事大学,2008.

[7]卢敏,张展羽,石月珍.集对分析法在水安全评价中的应用研究[J].河海大学学报(自然科学版),2006,34(5):505-508.

[8]曲径,沈崇松.基于集对分析理论的深圳港铜鼓航道危险度评价[J].天津航海,2009(4):10-12.

[9]邓雪,李家铭,曾浩健,等.层次分析法权重计算方法分析及其应用研究[J].数学的实践与认识,2012,24(7):93-100.

[10]陈俊英，张冰.基于熵的复杂系统的脆性理论基础研究[J].微计算机信息，2008(4)：55-58.

[11]齐迹.基于突变理论的海上交通风险预测研究[D].大连：大连海事大学,2014.

[12]唐舟进，任峰，彭涛，等.基于迭代误差补偿的混沌时间序列最小二乘支持向量机预测算法[J].物理学报，2004(5)：55-58.

[13]田丽娟，张矢宇，李娜.长江干线水上交通安全实时预警指标体系研究[J].交通信息与安全，2013(2)：24-28

[14]席永涛.人为失误与海上事故发生的机理分析[J].上海船舶运输科学研究所学报，2006(1)：35-39.

[15]张晶晶，赵志忠，向桂兵.高速公路交通安全管理系统研究[J].北方交通，2012(1)：57-60

[16]谭箭，周彩云，谢卓廷.交通冲突技术在水上交通领域的运用[J].武汉理工大学学报(交通科学与工程版)，2012(2)：87-90.

[17]邓良爱，刘明俊，刘佳仑.对长江干线航道信息指标系统的思考[J].武汉理工大学学报(交通科学与工程版)，2012(4)：200-205.

[18]曹宇，刘雅丽，王东，等.三峡船闸通航安全预警指标体系研究[J].水运科学研究，2008(2)：105-110.

Study on the Risk-Identification Model of the Ro-Ro Passenger Ship′s Sailing Based on the Brittle Link Theory

CHEN Houzhong1)HUANG Ying1)GUO Guoping1,2)

(SchoolofNavigation,WuhanUniversityofTechnology,Wuhan430063,China)1)(HubeiInlandShippingTechnologyKeyLaboratory,Wuhan430063,China)2)

Abstract：The paper carries out the model of SHEV which focuses on the Risk-Identification Ro-Ro passenger ship, and finds out 5 subsystems (brittleness factors) of the ship’s sailing. In addition, the weight of each factor and the weight vector Ai based on AHP are gained. After that, by setting pair analysis and empowering these brittleness factors, the brittleness correlation and brittle link entropy are calculated. At last, the Risk-Identification Model is put forward and put into practice based on the route from Beihai to Yangpu.

Key words：safety; the ro-ro passenger ship; brittle link theory; brittleness factors; brittle link entropy; the risk-identification model

收稿日期：2016-04-22

中图法分类号：U674.12

doi:10.3963/j.issn.2095-3844.2016.03.020

陈厚忠(1976- ):男，博士，副教授，主要研究领域为交通环境与安全保障、船舶控制理论与技术

*交通运输部2015年重点项目资助(跨海客运渡轮班线运营安全风险防控与示范)