基于近似L0范数算法的跳频信号时频分析

冯维婷, 梁　青, 谷　静

(西安邮电大学 电子工程学院, 陕西 西安 710121)

基于近似L0范数算法的跳频信号时频分析

冯维婷, 梁青, 谷静

(西安邮电大学 电子工程学院, 陕西 西安 710121)

摘要:针对跳频信号的参数化时频分析方法加以改进。对跳频信号进行完备傅里叶基表示，建立其稀疏优化表示模型，将跳频信号的时频分析问题转化为稀疏优化问题，然后借助近似L0范数优化方法进行时频分析。针对时长0.01 s的一段跳频信号进行计算机仿真，所得时频分布图显示，改进方法比短时傅里叶变换和WVD方法具有更高的时频分辨率和更强的抑制干扰能力。

关键词:时频分析；跳频信号；稀疏优化；近似L0范数

在跳频通信中，跳频信号的检测与参数获取十分重要[1-2]。在信号处理方法中，时频分析能描述信号频率随时间变化的特性，占据着非平稳信号分析的主导地位[3-4]。在各种时频分析方法中，短时傅里叶变换(Short Time Fourier Transform, STFT)[5]和小波变换(Wavelet Transform, WT)[6]由傅氏谱衍生而来，是线性时频分析方法的代表。STFT物理意义明确，但受测不准原理的制约，不能同时兼顾时频分辨率。WT克服了STFT的窗口大小不随频率变化的缺点，具有多分辨特性，但其窗口大小变化不具有自适应性。魏格纳分布(Wigner-Ville Distribution, WVD)是非线性时频分析方法的典型代表，具有较高的时频聚集性，但在多分量信号分析中存在交叉干扰项[7]，其改进方法如平滑伪WVD分布(Smoothed Pseudo WVD, SPWVD)[8]，也未能完全消除交叉项，而且这类方法对噪声敏感，在信噪比不高的场合下，不易获得良好的时频分析效果。

本文拟根据跳频信号在频域表现出的稀疏特性，将其用完备傅里叶基函数线性表出，建立起稀疏线性模型，将跳频信号的时频分析问题转化为带约束条件的稀疏优化问题，利用基于近似L0范数的稀疏优化方法求解，得出跳频信号的时频分布。

1信号的稀疏优化模型

1.1跳频信号建模

跳频信号可表示为

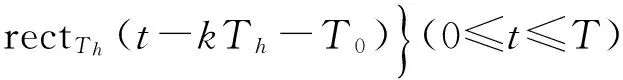
其中Q观测时间段内的频率跳变个数,fk为第k个载波频率,Th为每个跳频的持续周期，T0为观测时间内第一跳频的持续时间,rectTh表示窗口宽度为Th的窗函数。

接收信号不可避免地混有噪声，表示为

y(t)=s(t)+v(t)。

其中v(t)是方差为σ2的零均值复高斯白噪声。

将观测时间内的接收信号离散化，表示为

Y0=(y0,y1,…,yN-1)。

其中N为采样点数。将此N点时域数据分成K块，每块长度为P点，构造观测矩阵

Y=[y1,y2,…,yk]。

其中

yi=[y(i-1)P,y(i-1)P+1,…,yiP-1]T

(i=1,2,…,K)。

构造完备傅里叶基矩阵

W=[w0,w1,…,wP-1]。

其中

(i=0,1,…,P-1)。

接收信号在完备傅里叶基上的展开式为

Y=WX+V。

(1)

1.2信号的稀疏优化表示

在一段观测时间内，所接收跳频信号的频率跳变点有限(Q≤N)，即跳频信号具有稀疏性。X的求解可转化为稀疏重构问题

其中‖X‖0表示矩阵X中非零元素的个数。该稀疏重构问题的L0范数极小化求解是NP问题[9-10]。

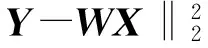
选择合适的参数λ，则此带约束最优化问题可以转化为无约束的最优化问题

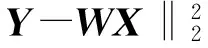
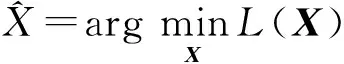
(2)

其中参数λ是噪声抑制平衡因子，其大小表征对噪声抑制能力的强弱。取值过大会削弱信号真实时频点处的幅度，取值过小则对噪声抑制能力弱。λ的最优取值[11]为Q/4。

2近似L0范数的稀疏优化算法

现有稀疏信号重构方法中,近似L0范数需要样本数少，计算量小且分辨精度高[12-13]。可采用平滑的高斯函数来逼近L0范数。

对于长度为N点的稀疏信号

X=(x0,x1,…,xN-1)T,

定义函数

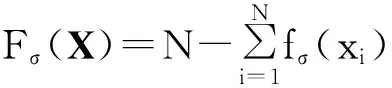
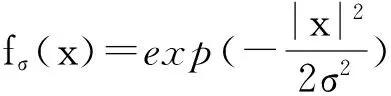
由于

所以

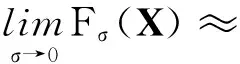
由此近似表示稀疏信号X的L0范数，可将无约束稀疏优化问题(2)转化为高斯和函数所表示的形式

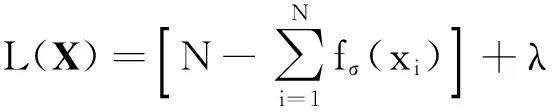
函数Fσ(X)的复共轭梯度为[14-15]

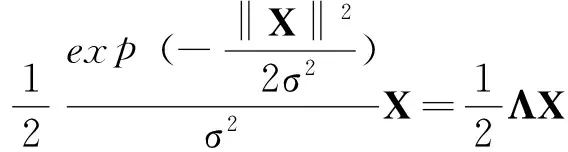
其中X*表示X的共轭，XRe和XIm分别表示X的实部和虚部,而Λ为对对角矩阵，其对角元素

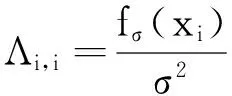
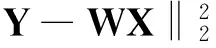
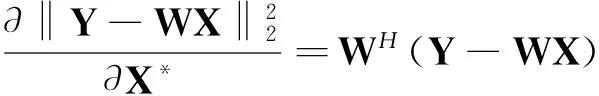
可得目标函数L(X)的复共轭梯度

。

当目标函数L(X)连续可微时，可采用迭代方法求稀疏解，即从初始值X(0)出发，沿着目标函数的复共轭梯度方向最速下降，经过迭代逐步逼近最优解。迭代形式为

X(k+1)=X(k)-μ(k)L(X(k))。

其中μ(k)为第k次的迭代步长。

3跳频信号时频分析步骤

跳频信号时频分析近似L0范数算法的具体实现步骤可描述如下。

步骤1输入测量值列向量Y，完备傅里叶基矩阵W及容许误差ε>0。

步骤2初始化X=X(0)，即令X(0)为Y=WX的最小二乘解。

步骤3选择高斯函数的一组按降序排列的参变量(σ1,σ2,…,σJ)(σ1>σ2>…>σJ)。

步骤4开始迭代，即令σ=σ1，计算复共轭梯度函数L(X)。

X=X-μL(X)。

否则，跳回步骤2，直到σ=σJ执行结束。

当σ近似为0时，目标函数L(X)高度不平滑，会使求解收敛于局部最优解。选择降序排列的参变量，采取从σ1(较大正常数)开始逐步靠近σJ(近似为0)，可使求解收敛于全局最优解。

4仿真实验

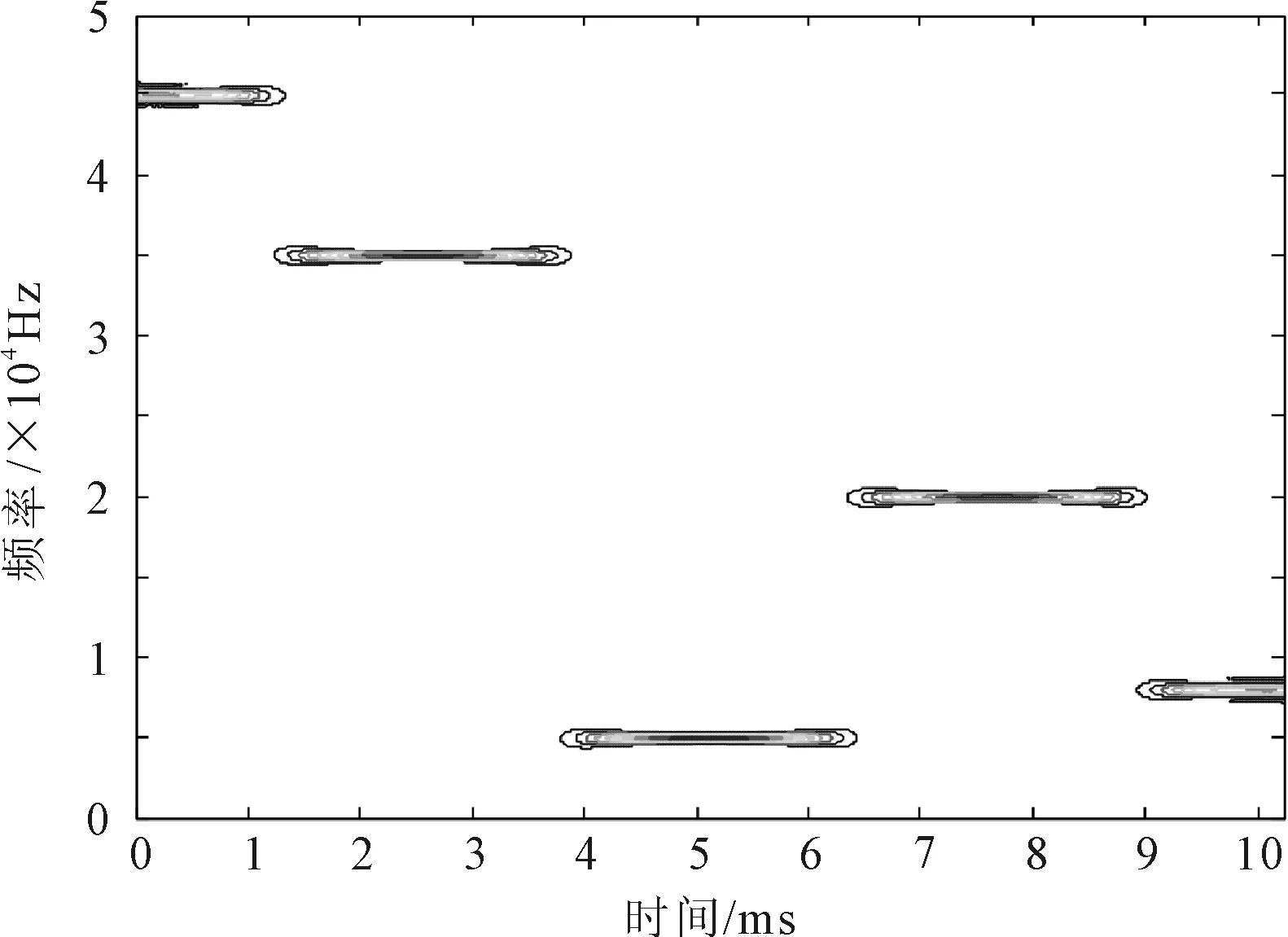
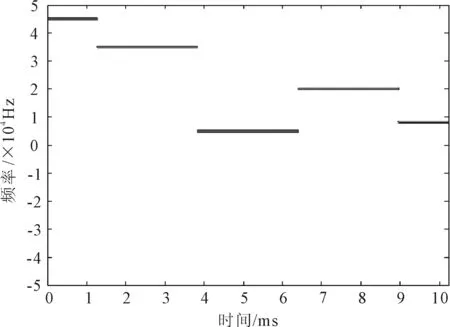
实验1产生一段跳频信号，第一跳频的持续时间为128个采样点，跳频频率序列为(45，35，5，20，8)(单位：kHz)，采样频率fs为100 kHz,采样点数N=1 024，跳周期为256个采样点。跳频信号的时频分布如图1所示。

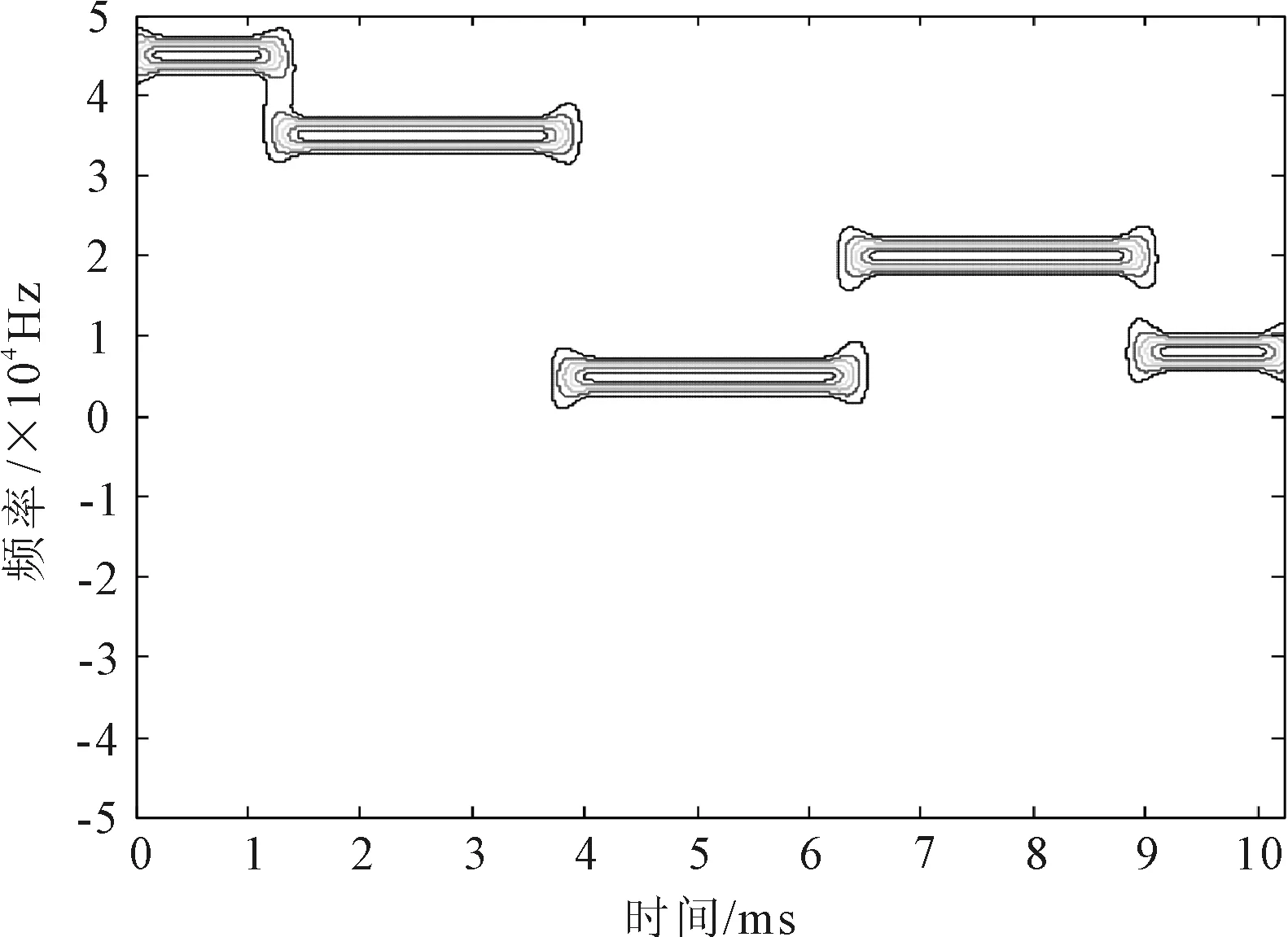
(a) STFT方法

(b) SPWVD方法

(c) 近似L0范数稀疏优化方法

采用STFT方法，选取长度为65点的汉明窗作为时间窗，短时谱的时间分辨率较高，但频率分辨率较差，跳频信号的时频分辨率不可兼得。采用SPWVD方法，可抑制交叉项，但会降低时频分辨率。采用稀疏优化方法，利用跳频信号的稀疏性，既无交叉项干扰，又能提高时频分辨率。

实验2在第1段跳频信号的基础上，附加产生第2段跳频信号，即第1跳频从0时刻开始起跳，跳频频率序列为(6，20，10，40)(单位：kHz)，采样点数N=1 024。产生复高斯白噪声，其信噪比为-2 dB。两段跳频信号的时频分布如图2所示。

(a) STFT方法

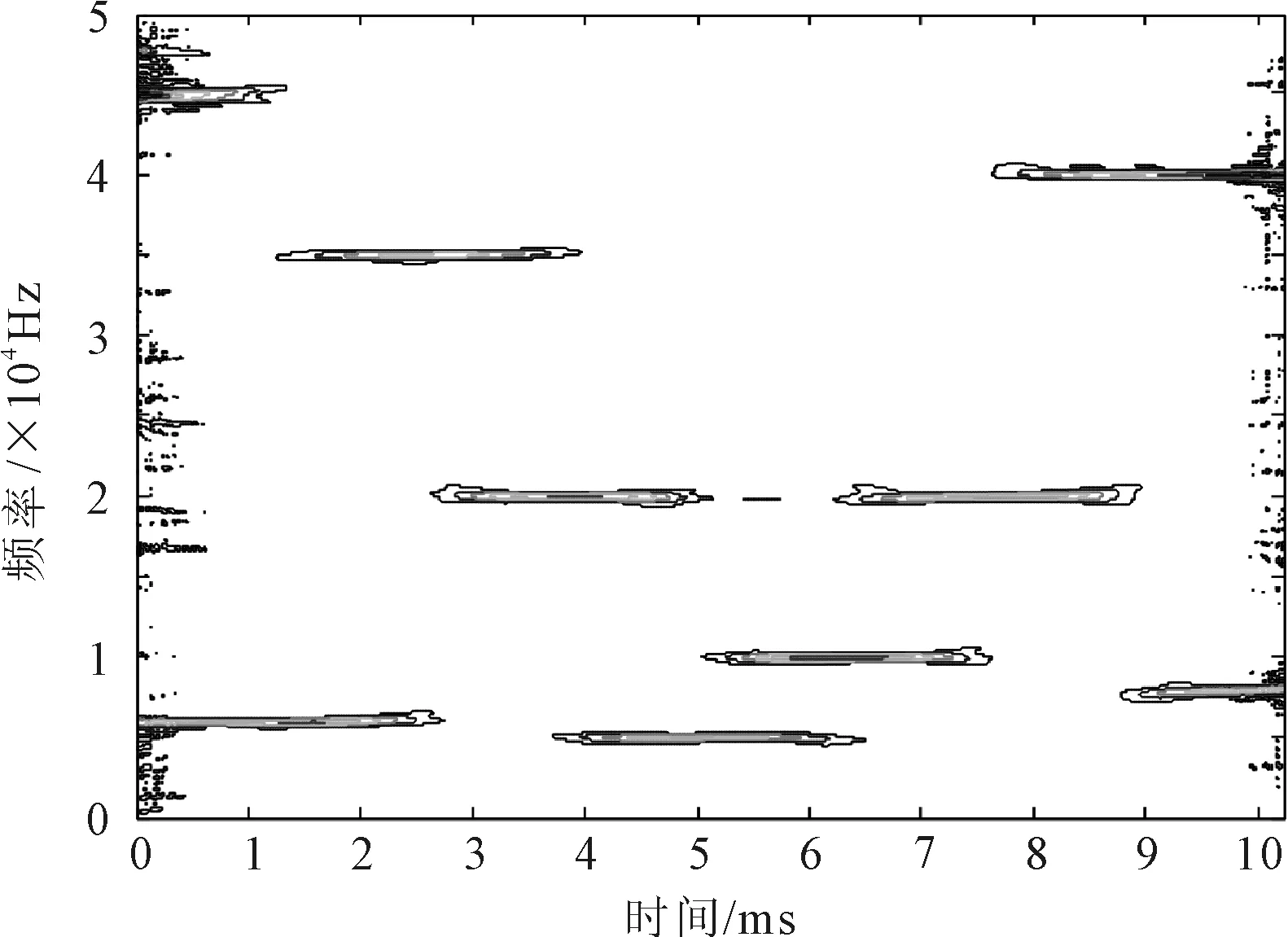
(b) SPWVD方法

(c) 近似L0范数稀疏优化方法

采用稀疏优化的时频分析方法较之STFT算法具有更强的抑制噪声能力。采用SPWVD方法时，多信号各自的跳变时刻清晰度降低，而采用近似L0范数稀疏优化方法，则可清晰分辨多信号的跳变时刻。近似L0范数稀疏优化方法更适合于多跳频信号的时频分析。

实验说明，基于近似L0范数的时频分析算法，较之STFT算法和SPWVD算法具有更高的时频分辨率和更强的抑制噪声能力。

5结语

建立信号的稀疏表示模型，将基于近似L0范数的稀疏优化方法引入到跳频信号的时频分析中，得出一种跳频信号时频分析的稀疏优化方法。仿真结果可以验证，该方法的时频分析性能优于STFT和SPWVD等时频分析方法。

参考文献

[1]梅文华. 跳频通信[M]. 北京: 国防工业出版社, 2005:5-16.

[2]TORRIERI D J. Mobile frequency-hopping CDMA systems[J]. IEEE Transactions on Communication, 2000, 48(8):1318-1327.

[3]科恩.时-频分析：理论与应用[M].白居宪，译.西安：西安交通大学出版社，1998:5-38.

[4]周浩,文必洋,吴世才,等.应用时频分析进行高频雷达射频干扰抑制[J].电子学报, 2003,32(9): 1546-1548.

[5]ZHONG J G, HUANG Y. Time-Frequency representation based on an adaptive Short-Time Fourier Transform [J].IEEE Transactions on Signal Processing,2010,58(10)：5118-5128.

[6]吕建平,彭述.一种基于SIFI的DWT域抗几何攻击水印算法[J].西安邮电大学学报, 2015,20(2): 88-92.

[7]冯涛,袁超伟.跳频信号的时频分析新方法[J].北京邮电大学学报, 2010,33(3): 10-14.

[8]赵俊，张朝阳，赖利峰.一种基于时频分析的跳频信号参数盲估计方法[J].电路与系统学报,2003,8(3):46-50.

[9]AMALDI E, KANN V. On the approximability of minimizing nonzero variables or unsatisfied relations in linear systems[J]. Theoretical Computer Science,1998,209(12): 237-260.

[10] TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12):4655-4666.

[11] 王军华,黄知涛,周一宇,等.基于近似L0范数的稳健稀疏信号重构算法[J],电子学报, 2012,40(6): 1185-1189.

[12] 张正炎,屈小波,林雁勤，等.基于近似LO范数最小化的NMR波谱稀疏重建算法[J].波谱学杂志, 2013, 30(4): 528-540.

[13] 杨良龙,赵生妹，郑宝玉，等.基于SL0压缩感知信号重建的改进算法[J].信号处理,2012,28(6):834-841.

[14] 魏志强,张愿章.复共轭梯度法的结构[J].哈尔滨理工大学学报,2012, 17(4):122-126.

[15] 杨倩,梅华,钱锋.基于负曲率方向的复数域共轭梯度法[J].华东理工大学学报：自然科学版,2009, 35(4): 644-647.

[责任编辑:瑞金]

Time-frequency analysis of frequency-hopping signal based on approximate L0 norm algorithm

FENG Weiting,LIANG Qing,GU Jing

(School of Electronic Engineering, Xi’an University of Posts and Telecommunications， Xi’an 710121， China)

Abstract:An improved parametric time-frequency analysis method based on sparse optimization is presented for frequency hopping (FH) signal. In this method, the FH signal is processed by complete Fourier basis, its sparse optimization model is constructed, and the time-frequency analysis is translated into a sparse optimization issue. The FH signal is then analyzed by the approximate L0 norm method. A computer simulation is carried out to test this method on a FH signal in the case of 0.01 s time length. The results of time-frequency pattern from this simulation show that the improved method has higher accuracy and better tolerance to noise than the STFT and WVD methods.

Keywords:time-frequency analysis, frequency-hopping signals, sparse optimization, approximate L0 norm

doi:10.13682/j.issn.2095-6533.2016.01.018

收稿日期：2015-06-27

基金项目：国家自然科学基金资助项目( 61202490)；陕西省自然科学基金资助项目(2014JM2-6117)；陕西省教育厅科学研究计划资助项目(15JK1654)；西安邮电大学青年教师科研基金资助项目(101-0486)

作者简介：冯维婷(1980-)，女，硕士，讲师，从事雷达与通信信号处理研究。E-mail:fengweiting11@163.com 梁青(1966-), 女，教授，从事无线传感器网络研究。E-mail: liangqing@xupt.edu.cn

中图分类号：TN911.7

文献标识码：A

文章编号：2095-6533(2016)01-0089-04