基于形状测度与最大信息熵函数的阈值法

张　弘， 郑培甜

(西安邮电大学 自动化学院, 陕西 西安 710121)

基于形状测度与最大信息熵函数的阈值法

张弘， 郑培甜

(西安邮电大学 自动化学院, 陕西 西安 710121)

摘要:针对光照不均匀、低对比度图像目标提取不完整的问题，提出融合应用形状测度与最大信息熵函数的图像阈值法。基于形状测度建立阈值化准则函数，应用像素点灰度或均值与梯度值建立共生矩阵，并得到最大信息熵阈值函数。兼顾形状测度对图像轮廓特征的获取及最大信息熵对图像边缘保留的特性，采用乘积的形式将两种函数进行融合，作为新的阈值选取准则。应用所提出的融合方法能够获得轮廓完整且边缘清晰的分割结果。

关键词:图像阈值法；共生矩阵；梯度；信息熵；形状测度函数

阈值法是一种经典的图像分割方法[1-7]。对于背景和目标具有显著差异的图像，可根据图像灰度直方图分布特性确定阈值[1-2]。对于目标与背景灰度值分布无明显界限的图像，还需结合图像像素点邻域空间的相关信息，如均值、中值与梯度[8-10]，构造共生矩阵，进行阈值选取。

共生矩阵的建立可基于灰度-均值[11-12]、灰度-中值[1-2]、灰度-梯度[13-14]、灰度-均值-中值[8]、均值-中值-梯度[9-10]，其中应用三维信息的方法，对背景情况复杂的图像阈值化比二维方法更好，但运算复杂度较高。

基于形状特征的图像检索和特征提取方法[15-16]从图像目标与背景的几何轮廓特征信息入手,进行图像分析，受灰度及邻域信息变化的影响小，也可用于图像分割阈值的选取。

基于共生矩阵的阈值法综合像素点与邻域信息建立阈值准则，侧重于像素点的空间特征。形态学方法通过图像几何轮廓特征的保留建立阈值准则，侧重于目标的几何特征。在图像采集过程中，实际环境、成像条件或者图像本身的灰度差异可能导致反光、灰度失真、对比度低等情况同时出现，此时，仅凭单一的方法已经难以实现良好分割。

本文拟应用形状测度函数，结合灰度与梯度、均值与梯度信息建立最大熵函数，针对光照不均匀、低对比度或目标与背景灰度分布界限不明显的图像进行目标提取，以求在保证目标提取完整性、轮廓清晰性的同时，保留纹理信息。

1基础算法其及应用分析

1.1形状测度函数及应用

形状测度函数可用以度量图像中目标物的几何特征，获得图像边缘的形态特性。当灰度级为t的形状测度函数FSM(t)取极大值时，对应图像G的轮廓特征最完整[17]。选用测度函数FSM(t)作为阈值化的准则函数，可得到最佳阈值

其中L为图像G的最大灰度级。

将图像G在点(x,y)的灰度值f(x,y)与t*作比较，可将分割后的图像表示为

选取两幅经典图像，如图1所示。车牌(number,730×203)图像存在一定的光照不均匀性，中部字母和数字的灰度值发生了变化。细菌(bacteria,256×256)图像因光照致使目标内部产生了一些反光的像素点，也使其灰度值发生了变化。应用形状测度函数实施分割,结果如图2所示。可见，车牌图像中字母和数字均能够被完整提取，细菌图像也获得了完整清晰的提取结果。

(a) 车牌 (b)细菌

(a) 车牌 (b)细菌

1.2基于灰度-梯度最大熵的阈值法

基于灰度-梯度的方法能够综合目标内部和边缘的信息[13-14]。

(1) 梯度信息获取

选取经典的米粒(rice)图像进行检测实验对比，为阈值计算确定边缘检测效果较好的梯度算子。参与对比实验的有Roberts算子、Sobel算子、Priwitt算子和Laplacian算子，以及形态学方法，结果如图3和图4所示。可见，Laplacian算子和基本的形态学方法均能有效提取图像的边缘信息，并保留了完整的目标轮廓特性，而且，前者比后者所获得的边缘完整性更为突出，故可考虑选用Laplacian算子进行梯度值的求解。

(a) 原图 (b)Roberts(c)Sobel(d)Priwitt(e)Laplacian(f) 形态学

图3米粒图像边缘检测结果

(a) 原图 (b)Roberts(c)Sobel(d)Priwitt(e)Laplacian(f) 形态学

图4含高斯噪声的米粒图像边缘检测结果

(2) 灰度-梯度共生矩阵

对一幅灰度图像分别进行灰度和梯度的归一化处理[13-14]，记其归一化灰度图像为F(x,y),归一化梯度图像为G(x,y)。以

C=(cij)Nf×Ng

表示灰度-梯度共生矩阵。矩阵C的元素cij表示灰度F(x,y)=i且梯度G(x,y)=j的像素点总数。这种像素点出现的概率

(3) 灰度-梯度最大熵法

若以灰度值t将图像划分为目标与背景两个区域,则目标区域A和背景区域B的信息熵可以分别表示为[13-14]

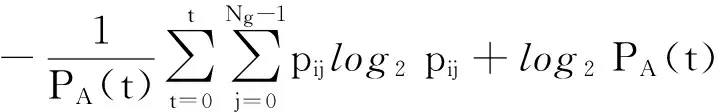
其中

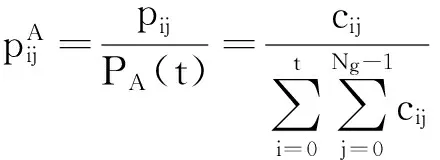
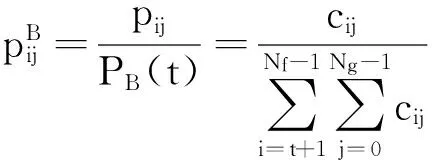
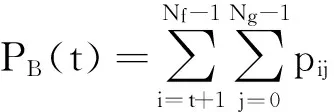
根据最大信息熵阈值选取原理，建立基于灰度-梯度的最大熵阈值选取准则函数

H(t)=HA(t)+HB(t),

由此确定用以图像分割的最佳灰度阈值

选取灯光(light，133×133)和电路(circuit,464×448)图像(图5)，应用由灰度-梯度最大信息熵确定的阈值进行图像分割，结果如图6所示。两幅原图的整个目标与背景灰度值均非常接近。分割结果显示，灰度-梯度最大信息熵方法同时兼顾了目标边缘信息和像素点内部信息，目标提取较为完整。

(a) 灯光 (b) 电路

(a) 灯光 (b) 电路

1.3基于均值-梯度最大熵的阈值法

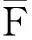
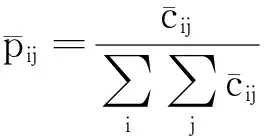
若以均值t将图像划分为目标区域A和背景区域B,则它们的信息熵可分别表示为

其中

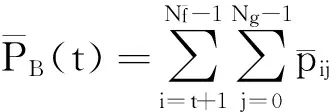
同样根据最大信息熵阈值选取原理，可建立基于均值-梯度的最大熵目标函数

由此确定用以图像分割的最佳灰度阈值

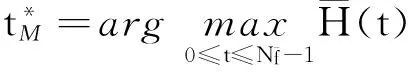
2两种方法的融合

2.1针对无噪图像的融合方法

形状测度函数侧重于图像几何轮廓特征的保留，对光照不均匀图像的分割有良好效果。灰度-梯度最大熵方法侧重于图像边缘的获取，在目标与背景灰度差异小，边缘信息模糊的图像分割中表现良好,但两种方法分别单独应用时，也会出现分割偏差。下文的对比实验部分对此会有说明。

为获得合理阈值，考虑将两种方法相互结合，兼顾形状测度法对几何特征的获取，以及灰度-梯度最大熵方法对边缘纹理的保留，得出一种融合方法，简记为SGG融合法。基于两种方法的阈值化准则，采用函数乘积的形式将两者的特点进行融合，构造新的阈值化准则函数

N(t)=FSM(t)×H(t),

则最佳的分割阈值

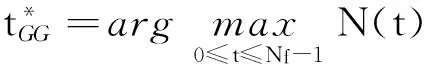
2.2针对含噪图像的融合方法

与灰度相比，均值具有一定抗噪性，抗高斯噪声的性能尤为明显。对于含噪声图像，可考虑应用均值-梯度共生矩阵代替灰度-梯度共生矩阵构造最大熵阈值算法。

将基于均值的形状测度法与均值-梯度最大熵方法相结合，可得出另一种融合方法，简记为SMG融合法。基于两种方法的阈值化准则，采用函数乘积的形式将两者的特点进行融合，构造新的阈值化准则函数

则最佳的分割阈值

3实验结果对比分析

3.1SGG融合方法

选取硬币(cion，216×236)、积水(watershed，228×122)和闹钟(clock，256×256)共3幅图像，进行二值化分割，以验证SGG融合法的正确性和有效性，并与单一的形状测度法、灰度-均值法、灰度-梯度最大熵方法进行对比。按照各方法相应理论确定的阈值如表1所示。实验结果分别如图7、图8和图9所示。

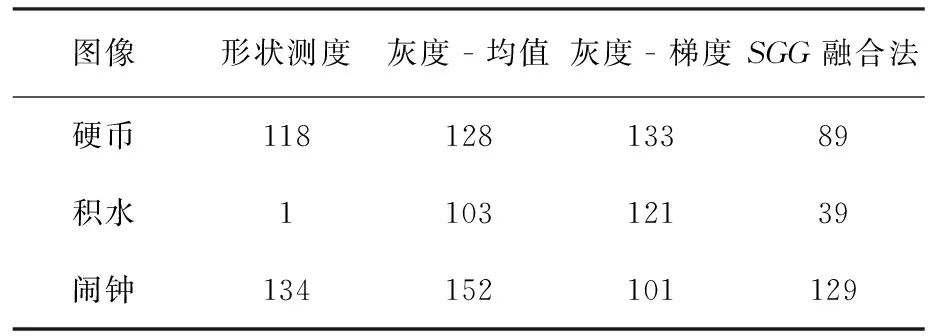
表1　针对各图像用不同方法所确定的阈值

(a) 原图(b) 形状测度法(c) 灰度-均值法(d) 灰度-梯度法(e)SGG融合法

图7硬币图像分割结果

(a) 原图(b) 形状测度法(c) 灰度-均值法(d) 灰度-梯度法(e)SGG融合法

图8积水图像分割结果

(a) 原图(b) 形状测度法(c) 灰度-均值法(d) 灰度-梯度法(e)SGG融合法

图9闹钟图像分割结果

实验所用待分割图像，皆存在一定程度的光照不均匀性，导致灰度失真，而且目标与背景灰度差异小、分布界限不明显。

图7和图8显示，单独应用形状测度法、灰度-均值法或灰度-梯度最大阈值法，得到的结果中均存在大量错分点。SGG融合法则从目标的完整性和边缘的清晰性方面得到提升。

图9显示，应用形状测度法可得到轮廓基本完整的结果，但边缘部分仍有不清晰之处，如钟表内部数字部分。应用灰度-均值法则出现了较多错分点。灰度-梯度最大阈值法对边缘纹理的保留最好，但SGG融合法在轮廓的完整性和边缘清晰性方面表现更好。针对图6(b)所示电路图像的对比实验结果与此类似。

另外，针对图1(a)所示车牌图像的对比实验显示，应用灰度-均值法、灰度-梯度最大阈值法，均不能实现正确分割，应用形状测度和SGG融合法可以达到完整清晰的分割结果，而且融合后的方法在边缘细节上更加清楚。针对图6(a)所示灯光图像的对比实验显示，应用形状测度法基本不能分割，应用灰度-均值法能实现分割，但边缘清晰度不如应用灰度-梯度最大熵阈值法所得结果，应用SGG融合法得到的轮廓完整性和边缘清晰性更好。

3.2SMG融合方法

选取加入均值为0，方差为0.002的高斯白噪声的米粒图像、硬币图像和摄影师图像，分别应用SGG融合方法和SMG融合方法对其加以分割。相关阈值如表2所示。实验结果如图10、图11和图12所示。可见，与基于灰度的方法相比，应用基于均值的方法，可使抗噪性能得到明显提高。

表2　针对含噪图像所确定的阈值

(a) 含噪图像 (b)SGG融合方法(c)SMG融合方法

图10含噪米粒图像分割结果

(a) 含噪图像 (b)SGG融合方法(c)SMG融合方法

图11含噪硬币图像分割结果

(a) 含噪图像 (b)SGG融合方法(c)SMG融合方法

图12含噪摄影师图像分割结果

4融合方法性能评价

采用有监督分割评价法中的误分类误差(MisclassificationError,ME)[18],作为客观评估标准,对SGG融合方法进行定量分析。

图像的误分类误差可以定义为

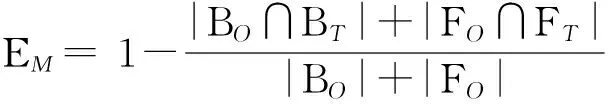
其中，BO和FO分别表示图像的真实背景和目标，BT和FT分别表示分割图像的背景和目标。

选取文献[19]提供的图像image12_r.bmp(168×54)和image23_r.bmp(551×227)，及其标准分割结果，采用误分类误差对SGG融合方法进行评价。

相关实验结果如图13和图14所示,对应的误分类误差值如表3所示。可见，SGG融合算法误分类误差值最小。

(a) 原图 (b) 标准分割图 (c) 形状测度法 (d) 灰度-梯度最大熵法(e)SGG融合方法

图13图像image12_r.bmp及其分割结果

(a) 原图 (b) 标准分割图 (c) 形状测度法 (d) 灰度-梯度最大熵法(e)SGG融合方法

图14　图像image23_r.bmp及其分割结果

5结语

融合形状测度法与灰度-梯度最大熵的图像分割阈值算法，可用以分割光照不均匀，及目标与背景灰度差异不明显的图像，兼顾目标完整性和边缘清晰性，分割准确率更高。应用像素点邻域均值代替灰度值参与信息熵构造，可提高分割算法的抗噪声性能。

参考文献

[1]章育晋.图像工程:中册[M].3版.北京：清华大学出版社, 2012:1-80.

[2]ANDREOPOULOSA,TSOTSOSJK. 50YearsofObjectRecognition:DirectionsForward[J].ComputerVisionandImageUnderstanding,2013,117(8): 827-891.

[3]MARN,ZHUY,DINGJD.Softimagesegmentationbasedoncenter-freefuzzyclustering[J].TransactionsofNanjingUniversityofAeronauticsandAstronautics, 2011,30(1): 67-76.

[4]ARBELAEZP,MAIREM,FOWLKESC,etal.Contourdetectionandhierarchicalimagesegmentation[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2011,33(5): 898-916.

[5]PENGB,ZHANGL,ZHANGD.Asurveyofgraphtheoreticalapproachestoimagesegmentation[J].PatternRecognition, 2013, 46(3): 1020-1038.

[6]赵凤,惠房臣,韩文超.基于过分割的多目标阈值图像分割算法[J].西安邮电大学学报,2015,20(3): 60-64.

[7]李琳,范九伦,赵凤.模糊C-均值聚类图像分割算法的一种改进[J].西安邮电大学学报,2014,19(5): 56-60.

[8]景晓军,李剑锋,刘郁林.一种基于三维最大类间方差的图像分割算法[J].电子学报,2003,31(9): 1281-1285.

[9]龙建武,申铉京,魏巍,等.基于均值-中值-梯度共生矩阵模型的最大熵分割算法[J].计算机应用研究,2010, 27(9): 3575-3578.

[10] 龙建武,申铉京,魏巍,等.一种结合纹理信息的三维Renyi熵阈值分割算法[J].计算机系统,2011, 32(5): 947-952.

[11]ABUTALEBAS.AutomaticThresholdingofGray-LevelPicturesUsingTwo-DimensionalEntropies[J].ComputerVision,Graphics,andImageProcessing, 1989,47(1): 22-32.

[12]BRINKAD.ThresholdingofDigitalImagesUsingTwo-DimensionalEntropies[J].PatternRecognition,1992, 25(8): 803-808.

[13] 周德龙,潘泉,张洪才,等.最大熵阈值处理算法[J].软件学报,2001,12(9):1420-1423.

[14] 张弘,范九伦.灰度-梯度共生矩阵模型的加权条件熵阈值法[J].计算机工程与应用,2010,46(6):10-13.

[15] 聂生显.基于形状特征的图像检索研究和应用[D].成都: 电子科技大学,2011:6-35.

[16] 刘璇,李海生,蔡强,等.三位形状特征提取技术研究进展[J].计算机科学与探索,2014,8(5):513-524.

[17]CHANGCI,DUY,WANGJ,etal.SurveyandComparativeAnalysisofEntropyandRelativeEntropyThresholdingTechniques[J].IEEEProceedingsVision,ImageSignalProcess,2006,153(6): 837-850.

[18]SEZGINM,SANKURB.Surveyoverimagethresholdingtechniquesandquantitativeperformanceevaluation[J].JournalofElectronicImaging, 2004,13(1): 146-168.

[19]SEZGINM.blt_image_references[Bs/OL].[2015-05-15].http://www.mehmetsezgin.net.

[责任编辑:瑞金]

Thresholdingmethodbasedonshapemeasureandmaximuminformationentropyfunction

ZHANGHong,ZHENGPeitian

(SchoolofAutomation,Xi’anUniversityofPostsandTelecommunications,Xi’an710121,China)

Abstract:A thresholding method based on the shape measure and maximum information entropy function is proposed to solve the problem of incomplete object detection of non-uniform lighting and soft image. A thresholding criterion function is built based on shape measure, the co-occurrence matrix is built by applying gray/neighborhood mean and gradient of pixels, and a maximum information entropy thresholding function is then obtained. The product of two functions is used as the new thresholding criterion function due to the consideration of the contour feature of shape measure function and the edge feature of maximum information entropy. The results show that the new proposed method can achieve the image of complete contour and clear edge, and that it is an effective thresholding method for non-uniform lighting and soft image.

Keywords:image thresholding, co-occurrence matrix, gradient, conditional entropy, shape measure function

doi:10.13682/j.issn.2095-6533.2016.01.009

收稿日期：2015-09-01

基金项目：国家自然科学基金资助项目(61571361,61340040,61102095);陕西省科技计划资助项目(2014KJXX-72);陕西省教育厅科学研究计划资助项目(15JK1682)

作者简介：张弘(1976-)，女，博士，副教授，从事模式识别与图像处理研究。E-mail:zhmlsa@xupt.edu.cn 郑培甜(1990-)，女，硕士研究生，研究方向为数字图像处理。E-mail:512684554@qq.com

中图分类号：TP391

文献标识码：A

文章编号：2095-6533(2016)01-0047-07