我心中的一次函数

江苏省江阴市利港中学八（7）班　王兴标



我心中的一次函数

江苏省江阴市利港中学八（7）班王兴标

函数的神奇和神秘之处，就在于和我们往常接触的数学知识不同.

1.它不同于计算，工工整整，顺理成章，简单易懂；

2.它不同于几何，有复杂多变的图形.

函数是一个抽象化的概念，打个比喻，函数如同一张大网，为什么这么说呢？请看下题——设直线l1：y1=k1x+b1与l2：y2=k2x+ b2，若l1⊥l2，垂足为H，则称直线l1与l2是点H的直角线.

（2）如图1，在平面直角坐标系中，四边形OABC的顶点A（3，0）、B（2，7）、C（0，7），P为线段OC上一点，设过B、P两点的直线为l1，过A、P两点的直线为l2，若l1与l2是点P的直角线，求直线l1与l2的解析式.

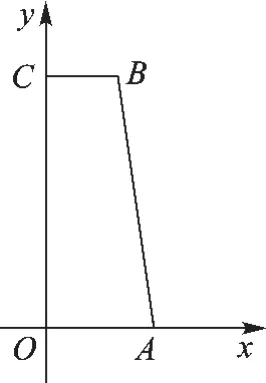
图1

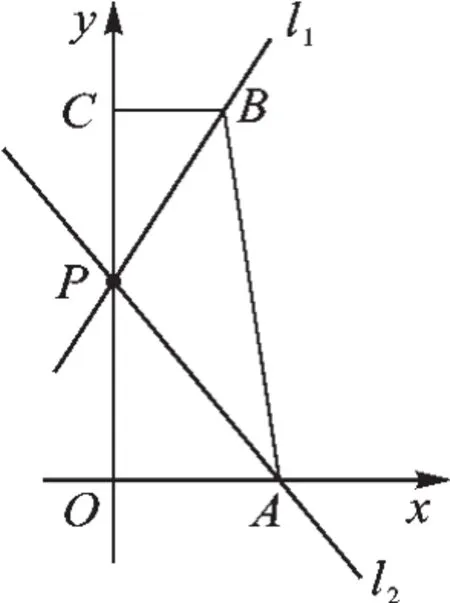
图2

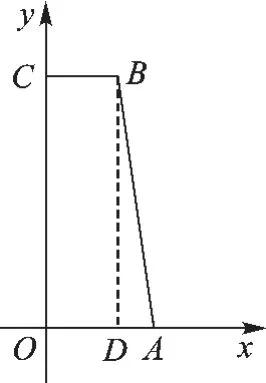
图3

【解析】第一问不难，画图正确，很明显可以发现①③是点C的直角线.此题主要难在第二问.首先要求直线l1与l2的解析式，就要先确定它的位置，如图2所示，在图中，可以发现有多个直角三角形，由此可以联想到勾股定理，观察图形，要求点P的坐标，由于点P在线段OC上运动，所以点P位置不确定，我们不妨采用“未知设元”，即设OP=x，则很明显CP=OC-OP=7-x，这里因为点A（3，0）、B（2，7），所以OA=3，BC=2，在Rt△OAP中，马上想到勾股定理，可得AP2=OA2+OP2，所以AP2=9+x2，同理在Rt△CBP中，由勾股定理得：BP2= 4+（7-x）2，题目中又已知l1与l2是点P的直角线，根据直角线的定义可以知道l1⊥l2，即AP⊥BP，马上想到通过Rt△APB的三边关系建立方程.这里还需要解决线段AB的长度，过点B作BD⊥AD，垂足为D（如图3所作），得D（2，0），即OD=2，进而得出AD =AO -OD =1，BD =CO =7，AB =.在Rt△APB中，由AB2=AP2+BP2，可转化为9+x2+4+（7-x）2=50.此方程最后化简为2x2-14x+12=0，这里很容易卡住——一元二次方程怎么解？我们没有学过啊！其实不然，还记得我们曾经学过的因式分解吗？对于方程的左边，我们进行十字相乘，得到（2x-2）（x-6）=0，故x=1或x=6.所以P（0，1）或（0，6）.当P点坐标为（0，1）时，直线l1的解析式为y=3x+1；直线l2的解析式为；当P点坐标为（0，6）时，直线l1的解析式为，直线l2的解析式为y=-2x+6.

解完此题后，思绪继续前行：

此题如果改为求△ABP的周长是多少，则此题就要进行分类讨论，当点P（0，1）时，可以求出△ABP的周长为，当P（0，6）时，△ABP的周长为.

回头观察已知条件：设直线l1：y1=k1x+ b1与l2：y2=k2x+b2，若l1⊥l2，垂足为H，则称直线l1与l2是点H的直角线，发现k1·k2= -1，这里让我联想起直线l1：y1=k1x+b1与l2：y2=k2x+b2如果平行，那么k1=k2，真是有趣！

我之所以比喻函数如同一张大网，是因为它将各方面的数学知识连接、汇合.例如该题很好地说明了函数是数与形的结合，这一道题就覆盖了“勾股定理”、“因式分解”、“未知设元”、“方程思想”、“分类讨论”等等.函数的神秘与神奇之处就在这里，完美结合数与形、连结各方面数学知识点，这便是函数独特的数学魅力所在.

刘老师点评：从小王同学这篇作品可以看出他钻研的真实心路历程.文中“联想”“马上想到”等词点出了他的顿悟过程.数学思想方法在小作者的解题分析的心路历程中得到完美的诠释，像发现点P在运动时，OP的长度就采用“未知设元”，在直角三角形中，马上联想到勾股定理、方程思想.当出现了一元二次方程这个没有学过的知识点时，小作者并没有放弃，反而激发了斗志，马上注意到方程左边的式子可进行因式分解，这种探究精神值得表扬！这里特别值得一提的是，小作者具有较好的数学素养，具体体现在解完题后，能自己提出问题（虽然这个问题的含金量不高，但具备这样的问题意识是值得称赞的），第二个问题渗透着由特殊到一般、归纳类比等思想.

（指导教师：刘杰）