水下滑翔机水动力外形优化配置*

赵远辉　李宝仁　高　磊

(华中科技大学机械学院　武汉　430074)

水下滑翔机水动力外形优化配置*

赵远辉李宝仁高磊

(华中科技大学机械学院武汉430074)

摘要：水下滑翔机升阻比是决定其滑翔经济性最关键影响因素，也是水下滑翔机优化设计的重要目标.论证了势流理论与湍流摩擦阻力计算相结合的方法在水下滑翔机水动力特性计算中的可行性，并采用该方法对水下滑翔机在滑翔状态下水平翼对滑翔经济性的影响进行了数值模拟研究.有助于进一步提高水下滑翔机的水动力性能.

关键词：水下滑翔机；升阻比；Hess-Smith面元法；滑翔经济性

0引言

水下滑翔机是一种无挂推进装置的系统，由净浮力驱动，主要通过沿主轴移动重物块调整自身重力与浮心间的相对位置改变俯仰姿态，实现水下滑翔机在垂直剖面内的锯齿状滑翔运动，可以实时获取水文监测数据.水下滑翔机的使用节省了监测成本、扩展了监测范围，成为海洋环境观测和海洋资源勘探的重要平台.水下滑翔机的续航时间和航程是评估滑翔机的总体性能优良的重要依据.水下滑翔机在配备高能电池外，应尽量提高其航行效率，以使得滑翔机在携带同样电量的情况下具有更长的续航能力和更大的航程.

目前，研制相对成熟并且相继投入科研任务的水下滑翔机主要有3种：Webb公司的Slocum、华盛顿大学的Seaglider，以及Scripps海洋研究所的Spray[1].这3类水下滑翔机壳体形状都属于细长回转体，这种设计可以保证一定装载量同时减小航行阻力，提高航行效率.国外学者首先针对航行效率提出了滑翔经济性的概念[2].该值大小与水下滑翔机升阻比相关.升阻比越大，水下滑翔机的滑翔效率越高，航行相同水平距离能耗越小.美国近期研制的新型大升阻比水下滑翔机“XRay”，“ZRay”可以以接近5°滑翔角滑翔，升阻比高达35，与传统水下滑翔机相比，航行效率提升了数十倍[3].

水下滑翔机水动力外形主要包括主体和附体2部分，且主体和附体的外形直接决定了其水动力特性.优化水动力外形是提升滑翔效率的直接手段.载体外形优化设计的原则为：在满足有效空间的前提下，应尽量降低载体水阻力，提高升阻比.本文采用势流理论的方法，计算出有攻角情况下主体和水平翼的外流场分布特性，并与有限元仿真结果比较，验证了方法的可行性.后在保持水下滑翔机壳体外形尺寸不变的情况下，通过改变水平翼的弦长、展长要素，得到不同翼与壳体组合下的水动力变化趋势.计算的结果为水下滑翔机的外形水动力性能设计提供参考.

1水下滑翔机水动力外形建模

图1　水下滑翔机外形轮廓图

水下滑翔机的计算模型见图1.水下滑翔机载体由主体、水平翼和固定尾鳍构成，图中的坐标原点位于水下滑翔机壳体头部端点.滑翔机主体外壳直径为0.24 m，长细比为10，头部尾部曲线段均由双参数椭圆方程确定[4]，方程中，椭圆指数影响较大，涉及主体阻力、主体丰满度以及湿表面积等参数，需通过相关优化算法计算得到[5].曲线段轴向长度为0.4 m，中间段为1.6 m长的平行中体.具体的主体轮廓参考下述方程给出.

头部曲线段的物理线型方程：

中间圆柱段的物理线型方程：

尾部曲线段的物理线型方程：

上式为归一化处理后的结果.

水平翼对水下滑翔机能否实现滑翔运动起着关键作用，水下滑翔机要求水平翼在滑翔过程中尽量避免在翼表面发生流动分离现象，以减小航行阻力，同时水平翼应具有较大的升阻比，以提高两翼的工作效率.水下对称翼型主要可分为平板翼和曲面翼两种.一般来说，小攻角的滑翔情况下，曲面翼型不易发生流动分离现象，水动力性能优于平板翼型[6].但曲面翼的加工程序难度较大.初步选用NACA0015曲面翼，弦长0.1 m，展弦比10.

2水下滑翔机升阻特性计算

2.1升力计算

小攻角滑翔情况下，水下滑翔机的升力主要由水平翼提供.主体产生的升力在小攻角情况下不作考虑[7].升力产生主要是由于在有攻角滑翔时，翼上下表面压强分布不均匀，导致沿着滑翔速度的垂直方向分力存在.因此求解升力，需确定翼表面的压力分布情况.本文采用势流理论中Hess-Smith面元法辅助求解翼表面压力分布.

Hess-Smith面元法[8]主要是沿着水下滑翔机壳体与翼轴向进行面元划分，并假设各面元上分布强度未知的源汇和等强度的涡，在该假设下，流场的速度势满足拉氏方程：

(1)

物面边界条件设定物面法向速度为零：

(2)

联立式(1)、式(2)得到：

(3)

根据划分的面元，离散上式求解出水下滑翔机各点处速度势大小，并根据伯努利方程确定各点处压力大小Cpi.Cpi按定义可以表示为：

(4)

物体升力可以认为是沿着物面各面元法向的压力积分，写成求和形式：

(5)

式中:pi为i控制点处压力；α为攻角；φi为物面法向与弦长法向间的夹角，化简上式可得

利用cosφiΔAi=Δxi;sinφiΔAi=Δyi，式(6)写成

(7)

根据上述的理论也可以写出有攻角下的翼的压差阻力表达式：

简化代入翼的压差阻力：

(8)

2.2阻力计算

水下滑翔机在水中航行时，雷诺数是判断其所处外流场流动状态的重要指标.雷诺数的定义：

(9)

式中：v∞为无穷远处的流体运动速度；L为流体特征长度，对于水下航行器，一般取水下滑翔机机身长度；ν=1.065×10-6m2/s为水的运动粘度.对于外流场判断湍流的标准，一般认为临界雷诺数为5×105[9]，当雷诺数Re<5×105，壳体的外边界层全为层流边界层.当Re>2×106时，则是湍流边界层或者湍流流动占主要的混合边界层.水下滑翔机在水中航行速度一般为1～2 kn，在这种航行速度下(见表1)，水下滑翔机外流场湍流占主要成分.

表1　不同航速下雷诺数

水下滑翔机周围流场为湍流，对于阻力的计算，水下阻力分为摩擦阻力和压差阻力两类，水下滑翔机长细比大且航行速度慢，一般尾部不会出现边界层分离现象，因此压差阻力在总阻力中所占份额较小.当长细比λ=L/D>6时，摩擦阻力所占份额超过总阻力的80%，因此零升阻力是水下滑翔机阻力的主要部分，在水下滑翔机阻力的初步分析计算中，可以忽略阻力增量，只考虑零升阻力.阻力计算中将壳体和翼近似作水中平板处理.

分别在1～2 kn来流速度，零攻角情况下，将水下滑翔机壳体与翼表面沿着水平轴划分微段，壳体轴向微段个数为Nx，见图2.xi，yi分别表示第i个微段端点的横纵坐标值.

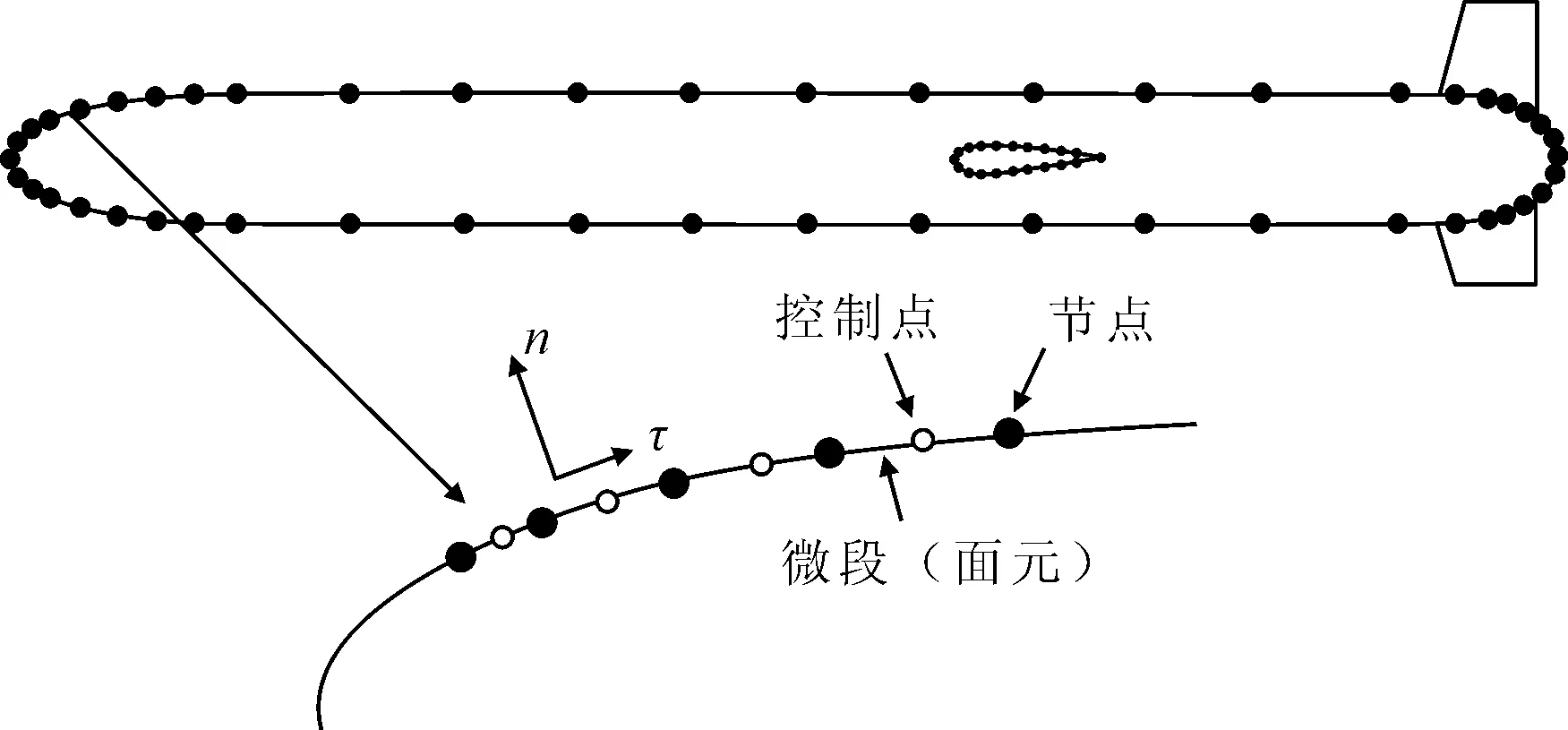
图2　水下滑翔机轴向微段划分

湍流条件下，壳体摩擦阻力系数按国际拖曳水池会议ITTC公式计算[10]，壳体在零攻角时的阻力系数.

(10)

根据摩擦阻力系数与摩擦阻力之间的关系，壳体零攻角时的阻力为

(11)

式中：ΩH为主体的湿表面积.

翼的阻力计算过程中，计算初期，可以忽略主体对翼周围外流场的影响，按照平板在水中摩擦阻力计算，且根据雷诺数计算得到翼外流场状态为层流，层流情况下摩擦系数为

(12)

翼的阻力：

(13)

式中：AF为翼的湿表面积；v∞为来迎流速度.

总阻力可以近似认为壳体和翼的阻力之和：

(14)

2.3算法验证

为验证上述数值计算的准确性，将水下滑翔机整体建模后导入有限元软件中进行水动力性能仿真计算，表2～3为不同航行速度下阻力及升力的数值计算值与仿真值的对比结果.由表2～3可见，计算结果和仿真结果吻合较好，最大误差为6.24%，验证了数值计算的可靠性.

图3　水下滑翔机模型网格划分

速度/kn壳阻力/N翼阻力/N总阻力/N计算值仿真值误差/%11.010.161.171.124.4623.330.453.783.643.84

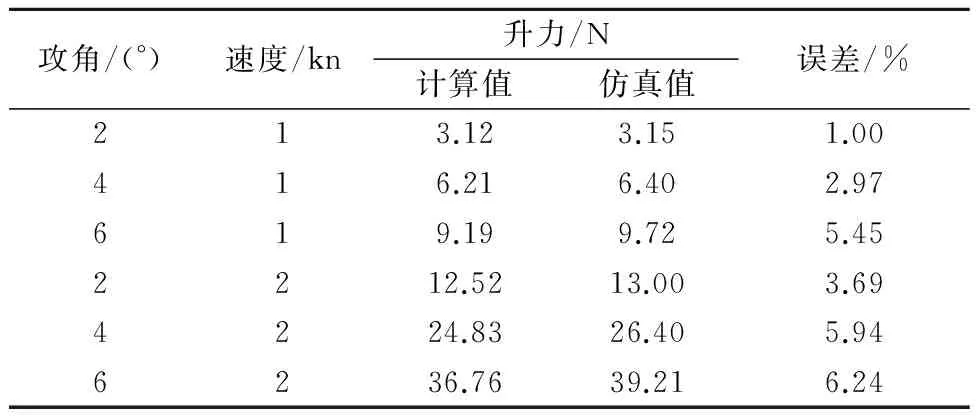
表3　升力数值计算结果验证

3壳体与翼优化配置

3.1计算内容

利用上述数值计算方法，在攻角α=6°，航速为2 kn的情况下，保持水下滑翔机壳体外形尺寸不变，通过改变水平翼的弦长、展长要素，组合得到不同配置方案，并针对各方案进行水动力特性计算，计算结果见表4～5.

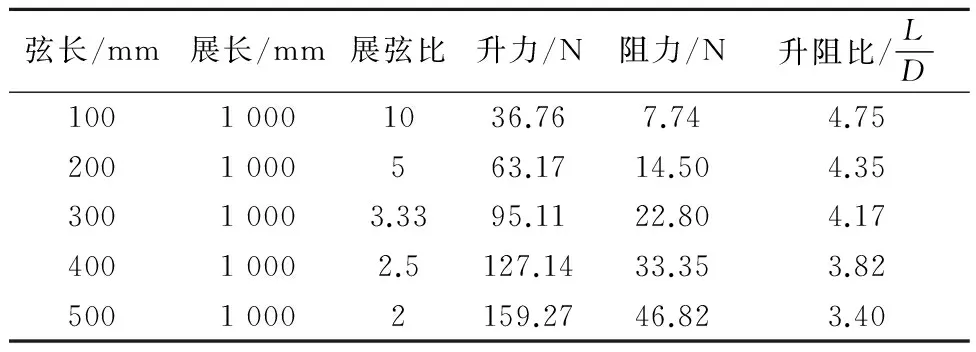
表4　变弦长数值计算结果

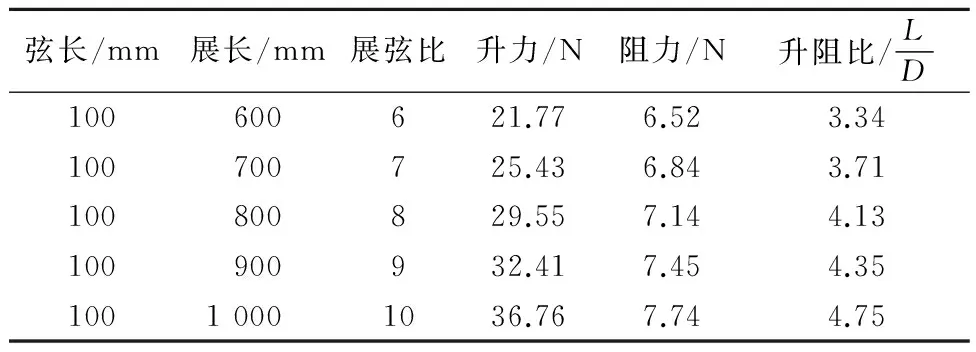
表5　变展长数值计算结果

3.2评判指标

水下滑翔机外形优化配置评判指标从滑翔经济性和最小滑翔角两方面设定，水下滑翔机在滑翔状态时滑翔纵剖面上的受力见图4.

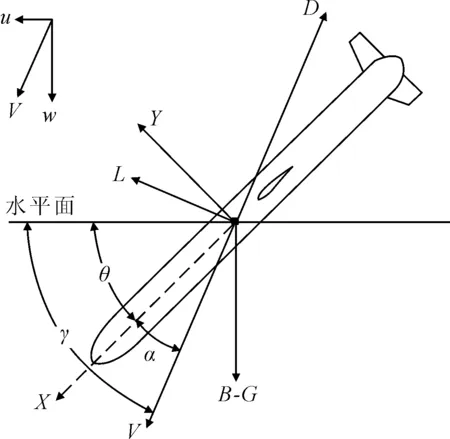
图4　滑翔中角度与受力示意图

水下滑翔机滑翔经济性量化标准根据滑翔经济性定义给出：

(14)

最小滑翔角由滑翔纵剖面上受力方程推导得出：

(15)

式中：Pe为单周期滑翔能耗量；u为水平航行速度；w为垂直航行速度；V为航行方向上的迎流速度；L，D，B-G分别为升力，阻力与净浮力；γ，θ，α分别为滑翔角，俯仰角与攻角；R，Δh分别为水平滑翔距离与滑翔深度.

通过上式描述关系得出：水平翼对水下滑翔机经济性的影响，可以由水下滑翔机的升阻比来评价，升阻比越大，滑翔效率越高，滑翔经济性越好.需要指出的是，本文分析中，滑翔的经济性仅从水动力角度进行探讨，其他影响因素例如机构能量转换效率等在这里暂不进行讨论.

最小滑翔角也由滑翔升阻比直接确定，最小滑翔角决定了指定深度条件下水下滑翔机单周期最远水平滑翔距离，是评估水下滑翔机滑翔性能的重要指标.

3.3结果与分析

通过比较不同翼与壳体的组合计算，从表4可以得出随着弦长的增加，展长固定，翼的展弦比减小.水下滑翔机受到升力与阻力均增加，但是阻力增加幅度更大，升阻比呈减小的趋势.相反从表5结果对比看出，弦长固定，展长增大，翼的展弦比增大，水下滑翔机受到的升力与阻力也均增加，此时升力增加幅度较大.升阻比呈上升趋势.改变弦长对升力、阻力的影响比改变展长影响大很多.仅从滑翔经济性考虑，应选取大升阻比配置，但综合安装可靠、布放回收简单等实际因素，最终选用弦长0.1 m、展长1 m的水平翼.

根据上节确定的升阻比带入式(15)计算，确定该配置条件下的最小滑翔角达到11.9°.下潜1 km深时，其水平滑翔距离可以达到9.5 km.

分析近期回收的海洋试验数据发现：样机在海洋环境稳定，外界干扰较小的情况下，单剖面下潜1 km深度，最远滑翔水平距离达到10 km，与计算值相比误差仅为5%，理论计算与实际吻合较好.

4结 束 语

本文叙述了应用势流理论中Hess-Smith面元法与湍流摩擦阻力计算相结合的方式求解水下滑翔机在低速湍流下的流场分布特性，通过该方法求解，取得了较好的数值计算结果，得到的压力、速度分布符合其在湍流条件下的分布规律，升力、阻力及其相关系数的数值计算结果与仿真结果相比，基本一致.采用该方法对不同翼与壳体组合下的方案进行水动力性能计算，分析得到给定主体下的最优翼的参数配置.为进一步水动力外形优化设计及配置提供了参考依据.

参 考 文 献

[1]武建国,陈超英,王树新，等.混合驱动水下滑翔器滑翔状态机翼水动力特性[J].天津大学学报,2010,43(1):84-89.

[2]JENKINS S A, HUMPHREYS D E, SHERMAN. Alternatives for enhancement of transport economy in underwater gliders[J].IEEE Proceedings of OCEANS,2003,2(2):948-950

[3] D’SPAIN, GERALD L, XRAY G. Scripps institution of oceanography[J]. Ocean Engineering,2012(2):56-62.

[4]ALVAREZ V, BERTRAM L, GUALDESI. Hull hydrodynamic optimization of autonomous underwater vehicles operating at snorkeling depth[J].Ocean Engineering,2009,36(1):65-71.

[5]庞永杰,王亚兴.Myring型回转体直航阻力计算及艇型优化[J].哈尔滨工程大学学报,2014(9):1093-1098.

[6]吴利红,俞建成,封锡盛,等.水下滑翔机器人水动力研究与运动分析[J].船舶工程,2006,28(1):58-61.

[7]潘光.鱼雷力学[M].西安:陕西师范大学出版社2013.

[8]黎昆,张志宏,顾建农,等.利用面元法计算潜艇在水底引起的压力分布[J].舰船科学技术,2014(36):29-32.

[9]胡克,俞建成,张奇峰,等.水下滑翔机器人载体外形设计与优化[J].机器人,2005,27(2):108-112,117.

[10]ALVAREZ A. Redesigning the SLOCUM glider for torpedo tube launching[J]. Ocean Engineering,2010,35(4):984-991.

Optimal Configuration for Underwater Glider Hydrodynamic Performance

ZHAO YuanhuiLI BaorenGAO Lei

(SchoolofMechanical,HuazhongUniversityofScienceandTechnology,Wuhan450074,China)

Abstract：The lift-drag ratio is the most crucial factor in determining the net transport economy. Besides, it is the important goal which the optimization design needs to achieve. This paper demonstrates the feasibility of using the combined method of the potential flow and turbulent friction in calculating the hydrodynamic characteristic of underwater glider. This numerical method is applied to analyze the impact of horizontal wings to the net transport economy under the motion of gliding. Efforts can be made for further improving the hydrodynamic performance of the underwater glider.

Key words：underwater glider; lift-drag ratio; hess-smith panel method; net transport economy

收稿日期：2016-05-11

中图法分类号：P715.5

doi:10.3963/j.issn.2095-3844.2016.03.023

赵远辉(1992- ):男，硕士生，主要研究领域为水下自航器水动力分析

*国家高技术研究发展计划(863计划)海洋技术领域项目资助(2012AA091002)