Barker线圈匀强磁场分析*

宋新昌

(中国船舶重工集团公司第七一〇研究所国防科技工业弱磁一级计量站　宜昌　443003)

Barker线圈匀强磁场分析*

宋新昌

(中国船舶重工集团公司第七一〇研究所国防科技工业弱磁一级计量站宜昌443003)

摘要以毕奥-萨伐尔定律为基础，运用椭圆积分，推导出单环线圈在空间任意一点产生的磁场公式，进而分析了亥姆霍兹线圈和四环Barker线圈在中心处磁场各分量的分布模型，绘出了空间分布图，分析结果表明：四环Barker线圈产生磁场的非均匀性小于0.0001的区域半径是亥姆霍兹线圈的21倍。

关键词椭圆积分; 磁场线圈; 磁场均匀性

Class NumberO441.3

1引言

为开展脉冲磁场治疗肿瘤技术的研究，首先要开发一台稳定可靠、磁场参数大、范围连续可调的脉冲磁场发生器。脉冲磁场发生器通常包括两个部分：1)脉冲电流的形成电路；2)磁场线圈。脉冲磁场线圈需要满足两个基本条件：1)线圈具有较小的电感；2)线圈内部具有较宽的均匀区域[1～2]。因为线圈的电感过大，不仅会增大脉冲磁场的脉冲前沿，还可能会引起输出波形的振荡；脉冲的均匀区域越大，对于医学实验研究越有利。

在治疗肿瘤用的脉冲磁场发生器的研究中，常用的是单线圈和亥姆霍兹线圈，它们因结构简单、加工方便得以广泛应用。但是单线圈和亥姆霍兹线圈的均匀度较低，要实现一定的均匀区，只能通过增大线圈的几何尺寸来满足。这样不仅增加线圈的电感，进而增大脉冲磁场的脉冲前沿，而且给加工制作带来不便，造成线圈搬运困难，特别是对线圈空间尺寸有严格限制时，常用的是单线圈和亥姆霍兹线圈无法满足设计要求[3～5]。针对以上问题，可以采用组合线圈的方式来实现。

2单线圈在空间任一点处产生的磁场

为了便于描述，建立如图1所示的座标系。

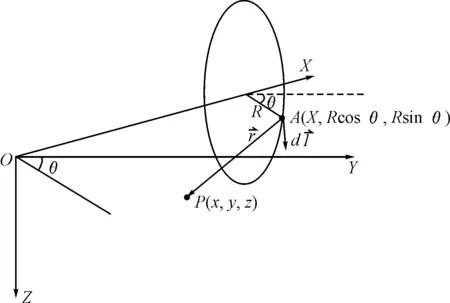
图1　线圈座标系

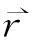
由图1可知：

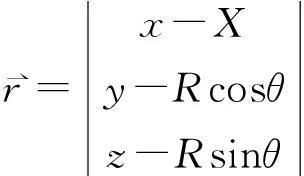
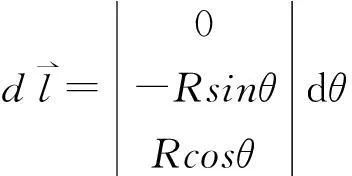
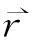
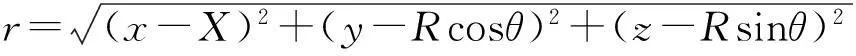
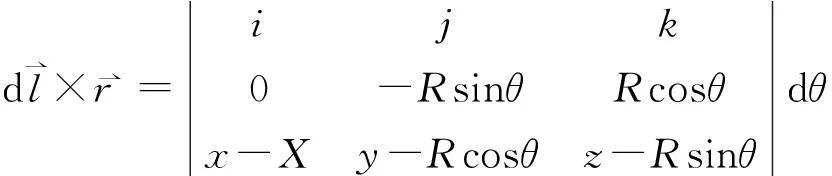
(1)

由毕奥-萨伐尔定律[6]得：

(2)

所以：

(3)

(4)

(5)

式(3)～式(5)为椭圆积分，用Maple数值分析软件[7]对上述三式求解，当y≠0、z≠0时，Bx≠0、By≠0、Bz≠0；当y=0、z≠0时，Bx≠0、By=0、Bz≠0；当y≠0、z=0时，Bx≠0、By≠0、Bz=0；这表明圆环线圈产生的磁感应强度不存在垂直于半径方向的螺旋分量。当y=z时，By=Bz；当y=C1、z=C2(C1≠C2)时，By=B1、Bz=B2；当y=C2、z=C1(C1≠C2)时，By=B2、Bz=B1；这表明圆环线圈产生的磁感应强度存在径向的对称性[8]。

3亥姆霍兹线圈产生的磁场分析

众所周知，当两个线圈的半径相等、匝数相等、间距等于线圈的半径、所通的电流大小相等方向相同时，中心点附近沿轴向分布的磁场较为均匀，这样放置的两个线圈称为亥姆霍兹线圈，由式(3～5)通过坐标变换可得亥姆霍兹线圈产生的各分量磁场如式(6)～(8)所示(式中X=0.25R)。

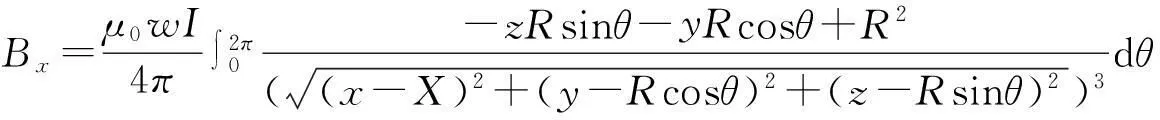
(6)

(7)

(8)

线圈中任一点处的磁场Bx(x,y,z)与中心点处的磁场Bx(0,0,0)的相对误差可以表示为线圈磁场的非均匀性IH，IH越小，磁场的均匀度越高[9]。

(9)

在此用Maple数值分析软件分析了半径为1m，匝数为1匝，电流为1A，线圈间距为0.5m时亥姆霍兹线圈产生的磁场，由于圆形线圈产生磁场的对称性，取z=0平面的磁场强度，表1给出了z=0平面轴向磁场Bx的非均匀性数据，图2、图3分别给出了z=0平面轴向磁场Bx的非均匀性图像及非均匀性小于0.0001和0.001的区域。

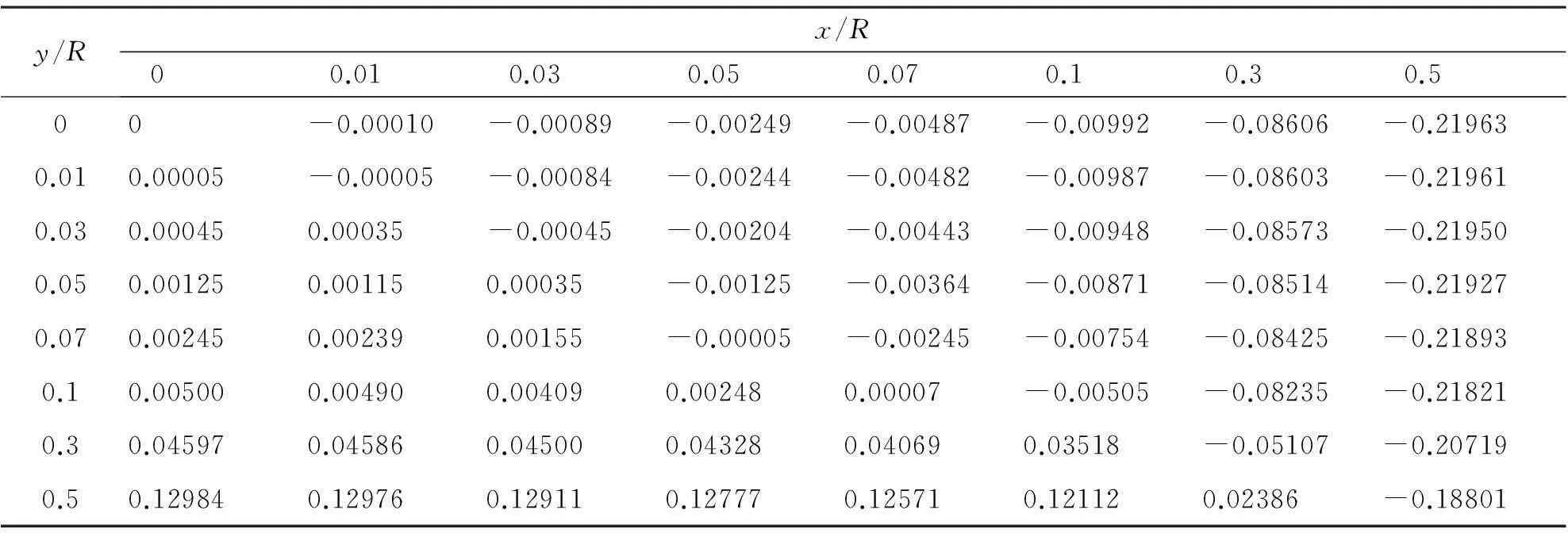
表1　z=0平面Bx均匀性数据

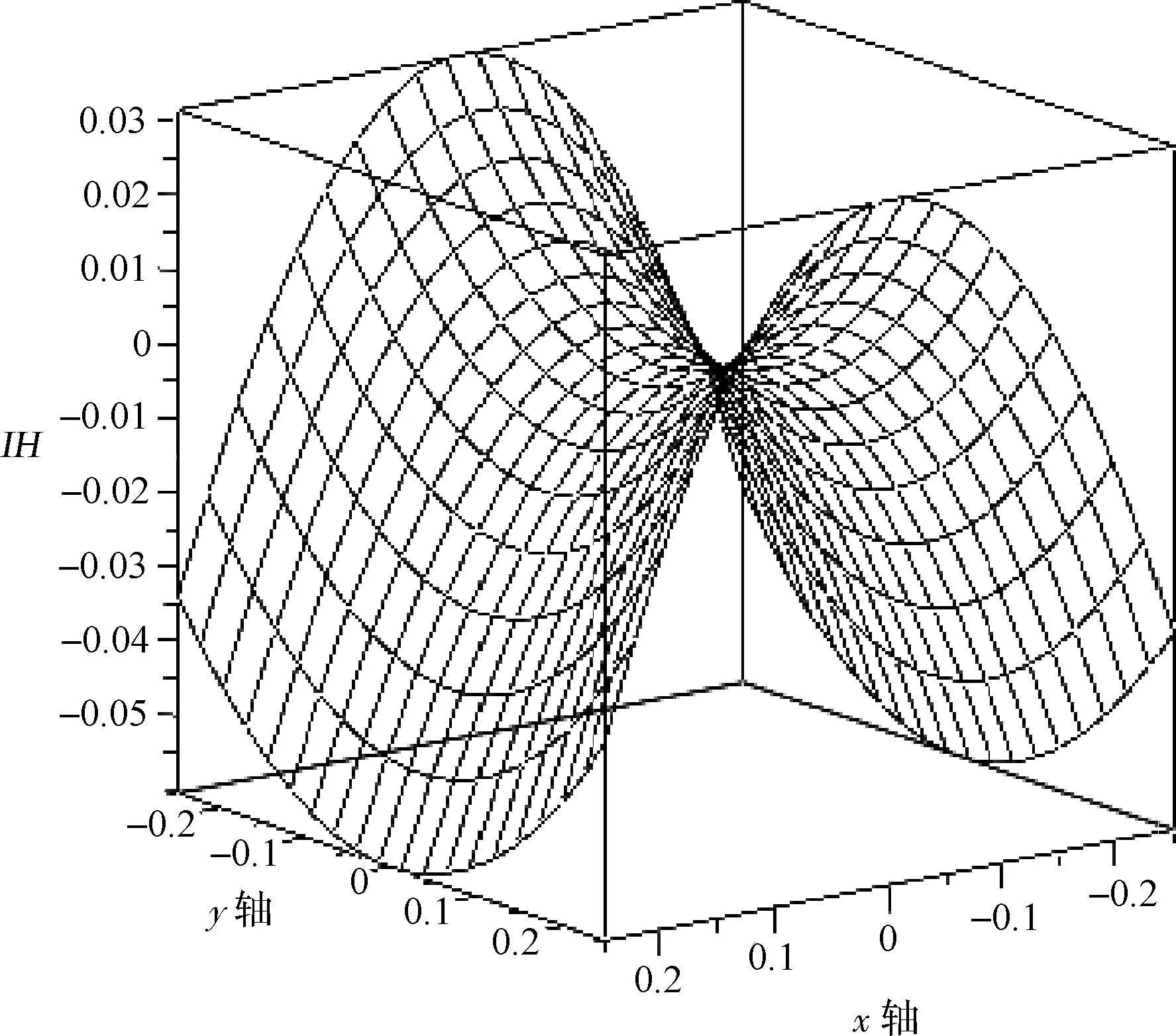
图2　z=0平面Bx非均匀性

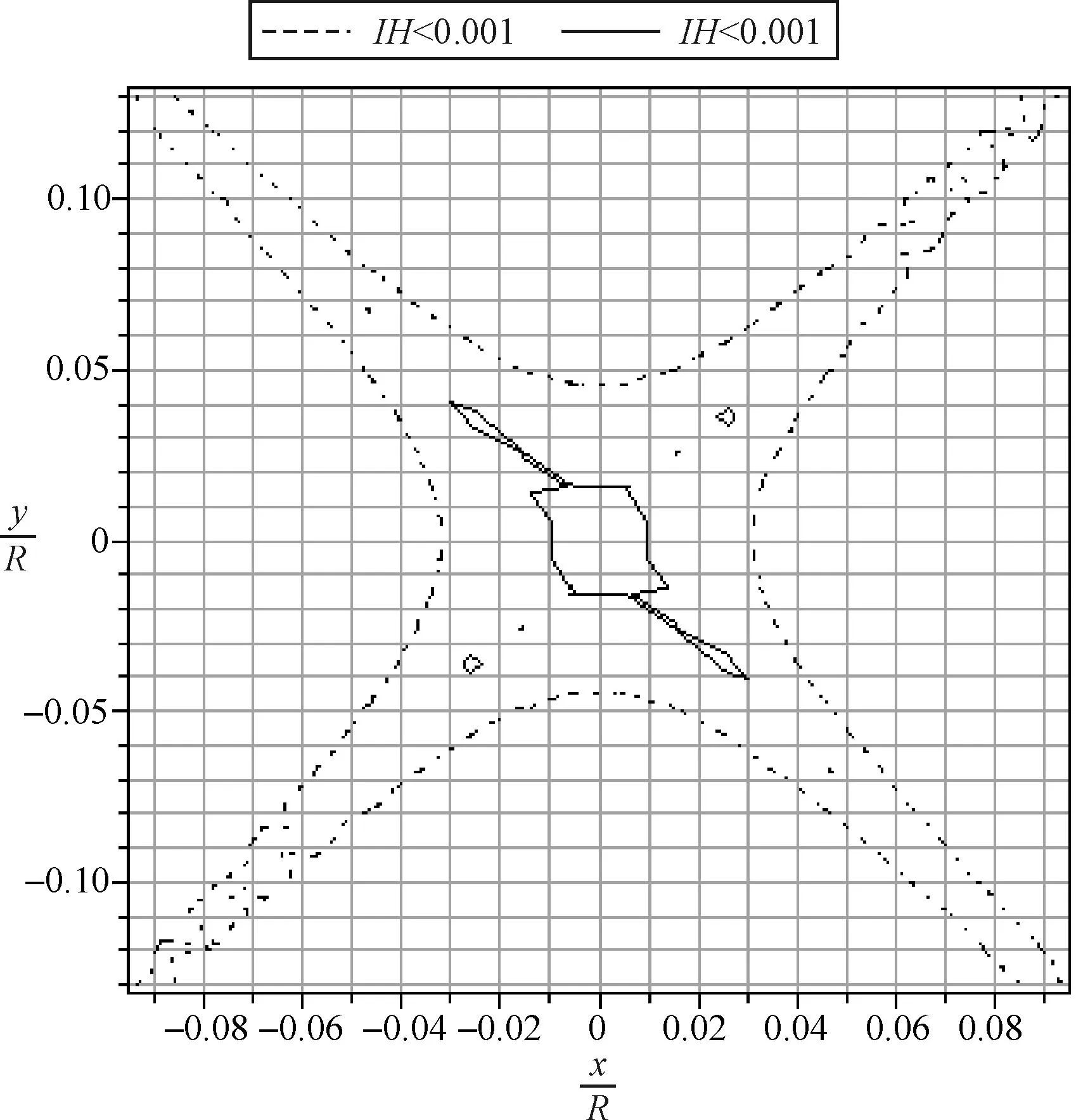
图3　z=0平面Bx非均匀性区域

由图2可以清楚的看到，亥姆霍兹线圈产生的轴向磁场强度Bx在z=0的平面内具有马鞍形结构，当x保持不变时，Bx随着y值的增大而增大；当y保持不变时，Bx随着x值的增大而减小，磁场具有对称性。由图3可以看到在z=0的平面内，轴向磁场分量Bx在x/R=0.01、y/R=0.015的区域内非均匀性小于0.0001；在x/R=0.03、y/R=0.045的区域内非均匀性小于0.001，其中非均匀性边界区域不规则可能是由于椭圆积分取近似的结果造成的。

由上述分析可知，亥姆霍兹线圈在中心点附近线圈半径1.5%的区域内产生轴向磁场的非均匀性小于0.0001，在中心点附近线圈半径3%的区域内产生轴向磁场的非均匀性小于0.001，所以亥姆霍兹线圈产生的磁场均匀性相对较低。

4四环Barker线圈产生的磁场分析

为了产生高度均匀的磁场，可以采用共轴的多组线圈系统来实现，各组线圈的位置和尺寸及匝数需要满足相应的参数，否则不能产生高度均匀的磁场，在此分析了四环Barker线圈系统[10]，这类系统的特点是各段线圈两两对称，处在公共圆柱表面上，亦即系统满足条件R1=R2=R(如图4)，所通电流的方向相同，系统的特点是简单及可能以很高的精度加工制作。则四环Barker线圈产生的磁场如式(10)～式(11)所示：

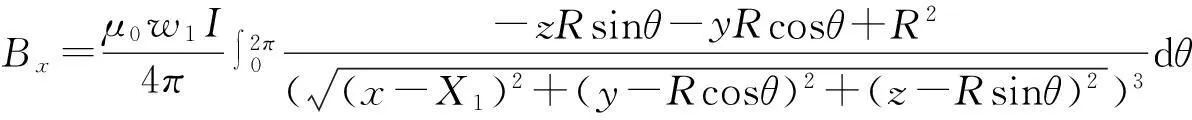
(10)

(11)

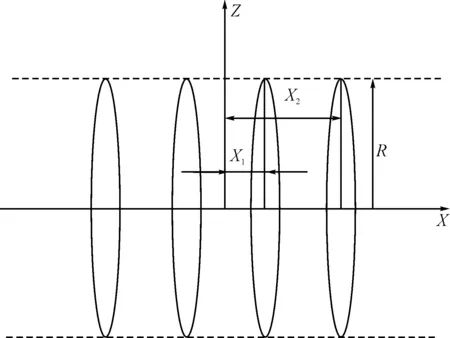
图4　四环barker线圈示意图

为了确定各段线圈的匝数、位置、半径等参数，借助Maple数值分析软件对Bx的表达式求x的一～八阶导数，然后把x=0、y=0带入各阶导数的表达式，其一、三、五、七阶导数的表达式由于Barker线圈系统的对称性等于0，二、四、六、八阶导数的表达式不等于0，在此令二、四、六、八阶导数的表达式等于0之后联立方程组，可以解出：X1/R=0.2432，X2/R=0.9407，w2/w1=2.2606。

在线圈加工过程中，Barker线圈所有各段圆环相串联，在接到公共电源上，这时要保证w2/w1=2.2606有一定的困难，这些缺点可以通过预先对结构做一些处理来消除。首先给出易于实现的匝数比，这个匝数比要尽可能的接近理论计算值，然后从均匀性条件出发，求出几何参数相应的微小增量。在此我们取w2/w1=7/3≈2.3333，则X1/R=0.2327，X2/R=0.9171，二阶导数k2=0、四阶导数k4=0、六阶导数k6=-0.074、八阶导数k8=-0.448，此时表征圆柱的条件并未受到破坏，但由于六阶导数不为零，从而降低了对均匀性的要求，这样的系统已经不是最佳系统，但由于六阶导数与八阶导数相比很小，对于实际应用来说，六阶导数是否为零并不重要。

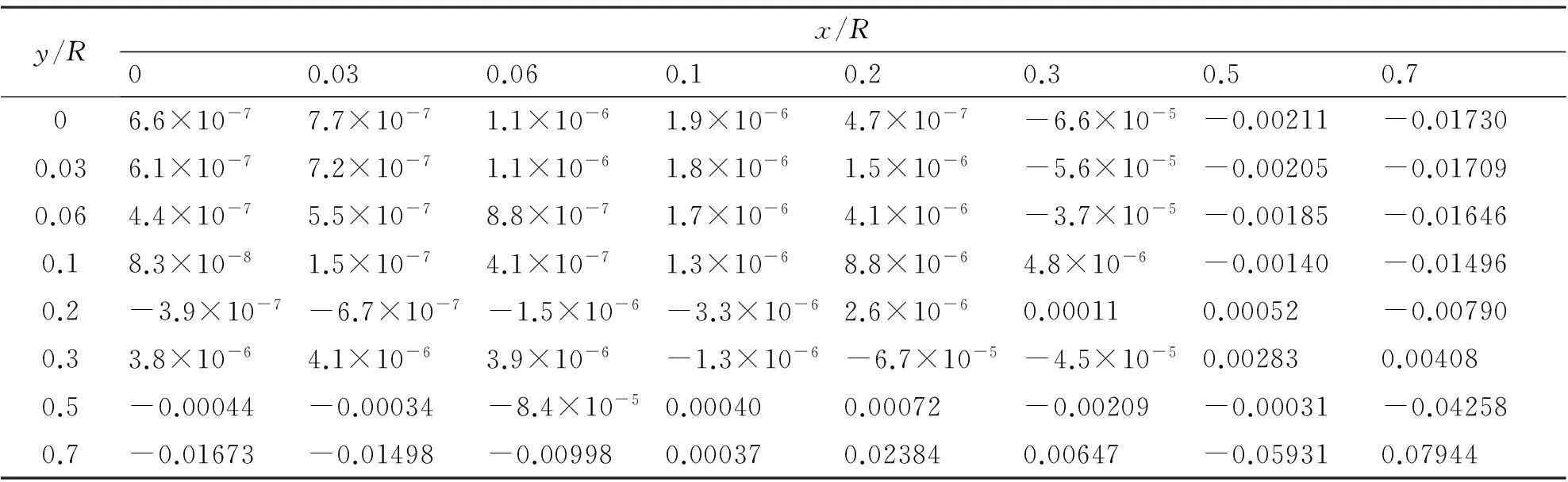
表2　z=0平面Bx均匀性数据

用Maple数值分析软件分析了R=1m，X1=0.2327m，w1=7匝；X2=0.9171m，w2=3匝，电流为1A的四环Barker线圈系统产生的磁场，由于圆形线圈产生磁场的对称性，在此取z=0平面的磁场强度，表2给出了z=0平面轴向磁场Bx的非均匀性数据，图5、图6分别给出了z=0平面轴向磁场Bx的非均匀性图像及非均匀性小于0.0001和0.001的区域。

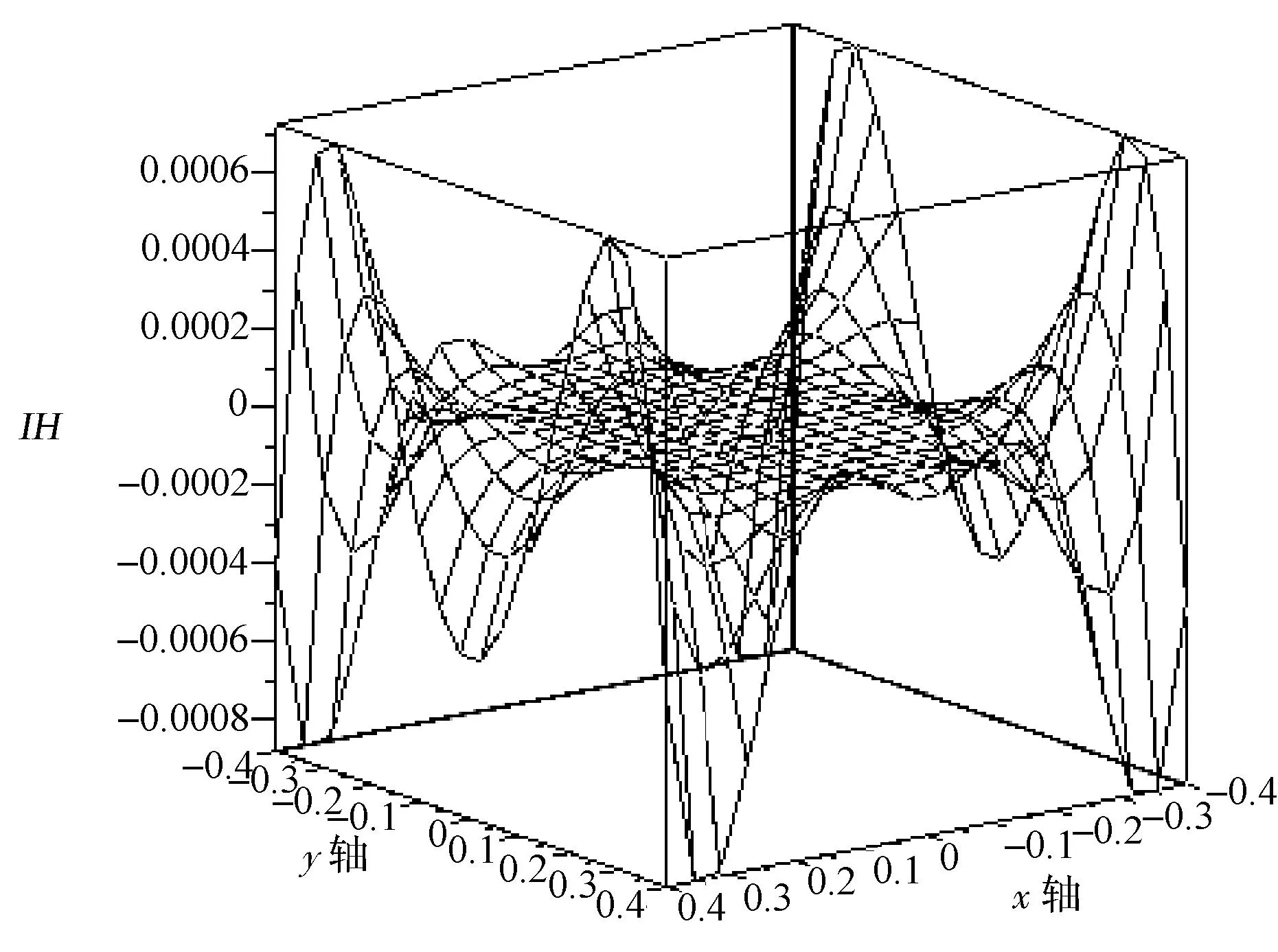
图5　z=0平面Bx非均匀性

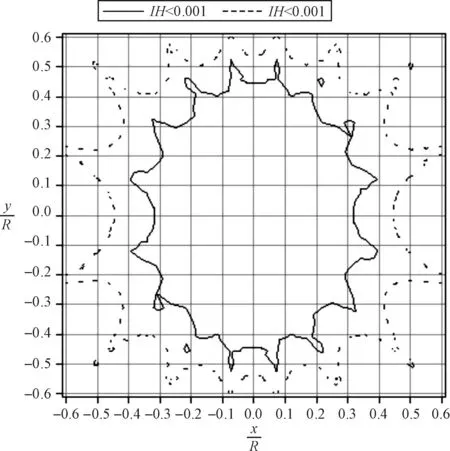
图6　z=0平面Bx非均匀性区域

由图5可以清楚地看到，由于两侧圆环的磁场调节作用，四环Barker线圈产生的轴向磁场Bx在z=0的平面内已经不具有马鞍形结构，但磁场具有对称性。由图6可以看到在z=0的平面内，轴向磁场分量Bx在中心点r/R=0.32的圆形区域内非均匀性小于0.0001；在中心点r/R=0.45的圆形区域内非均匀性小于0.001。

由上述分析可知，四环Barker线圈在中心点附近线圈半径32%的区域内产生的轴向磁场非均匀性小于0.0001，在中心点附近线圈半径45%的区域内产生轴的向磁场非均匀性小于0.001，所以四环Barker线圈产生的磁场均匀性相对较高。

5结论

本文以毕奥-萨伐尔定律为基础，运用椭圆积分，推导出单环线圈在空间任意一点产生的磁场公式，通过坐标变换分析了亥姆霍兹线圈和四环Barker线圈在中心处磁场各分量分布模型及图像，分析结果表明：四环Barker线圈产生的轴向磁场非均匀性小于0.0001的区域半径是亥姆霍兹线圈产生的轴向磁场非均匀性小于0.0001的区域半径的21倍，非均匀性小于0.001的区域半径是亥姆霍兹线圈的15倍。在一些实际应用中，若要产生高度均匀的匀强磁场或者线圈的体积不能做的太大，可以采用四环Barker线圈系统的结构形式。

参 考 文 献

[1] 米彦,李成祥,姚陈果.肿瘤治疗用陡脉冲磁场发生器的研制[J].高电压技术,2009,35(9):2226-2231.

[2] 梁可道.用于肿瘤治疗的陡脉冲磁场发生器的研制[D].重庆：重庆大学,2007.

[3] 佘守宪,张思炯.Helmhohz线圈、直螺线管及圆电流磁场均匀性分析的简单公式[J].大学物理,1999,18(8):1-3,6.

[4] 张伟.高均匀度磁场线圈的设计[J].计量学报,2010,31(5)：404-407.

[5] 邹志纯.亥姆霍兹线圈空间的磁场分布[J].西安邮电学院学报,2004,9(3):89-91.

[6] 赵凯华.电磁学[M].北京：人民教育出版社,1981:39-70.

[7] 何青,王丽芬.Maple教程[M].北京：科学出版社,2006:155-162.

[8] 雷银照.轴对称线圈磁场计算[M].北京：中国计量出版社,1991:35-143.

[9] 谭曦,刘军,殷建玲.正方形亥姆霍兹线圈的磁场均匀性[J].光学仪器,2012,34(1)：39-44.

[10] Ю.B.阿法拉谢耶夫.磁场参数测量器具[M].张伦,译.北京：科学出版社,1983.

[11] 张宝裕,刘恒基.磁场的产生[M].北京：机械工业出版社,1987.

Analysis of Barker Magnetic Field Coils with High Homogeneity

SONG Xinchang

(1st Class Weak Magnetic Metering Station of NDM, No. 710 R & D Institute, CSIC, Yichang443003)

AbstractBased on the biot-savart law, using elliptic integral, the magnetic field formula of single-ring coil in any space is deduced, each component of the magnetic field model are analyzed both in the center of the Helmholtz coils and four ring Barker coils, distribution diagrams is given. the analysis result show that the inhomogeneity area radius which is less than 0.0001, the four ring Barker coils is 21 times bigger than the Helmholtz coils.

Key Wordselliptic integral, magnetic coils, magnetic field uniformity

*收稿日期：2015年12月10日,修回日期：2016年1月17日

作者简介：宋新昌，男，硕士，研究方向：磁性材料及磁路设计。

中图分类号O441.3

DOI：10.3969/j.issn.1672-9730.2016.06.038