走出数据分析的“雾”区
2016-06-29朱元生
□朱元生
走出数据分析的“雾”区
□朱元生
用样本估计总体是统计的基本思想,通过对样本数据的分析来了解总体是统计的基本方法.然而少数同学对统计量的意义理解不透,常会产生这样那样的误区,现就几类比较常见的问题举例剖析如下,望能引起同学们的足够重视.
一、对加权平均数的“权”理解不够
例1东风超市备有某种绿色蔬菜100千克,上午按每千克1.2元的价格售出50千克,中午按每千克1元的价格售出30千克,下午按每千克0.8元的价格将剩下的蔬菜全部售完,试求这批蔬菜售出的平均价格是多少?
剖析:在3个不同时间售出的蔬菜中,由于售出蔬菜的重量不同,各个时间售出蔬菜的单价对平均价格的影响不同,因此这批蔬菜售出的平均价格不能简单地用3个时间售出蔬菜价格的算术平均数来表示,而应该用加权平均数来计算.
=1.06(元/千克).
答:这批蔬菜售出的平均价格为1.06元/千克.
二、对中位数的“中”理解不够
例2在一次中学生田径运动会上,参加男子跳高的15名运动员成绩如下表所示:
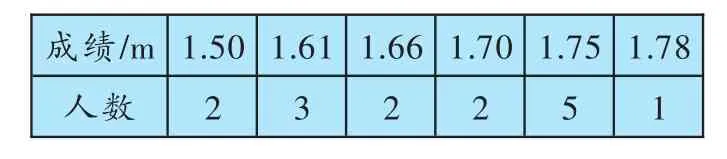
成绩/m __人___ __数1.50 _ 2__ __ 1.61 _ 3__ __ 1.66 _ 2__ __ 1.70 _ 2__ __ 1.75 _ 5__ __ 1.78 1_
则这些运动员成绩的中位数是多少?
剖析:从表中可以看出,跳高成绩有6个数值,错解就以最中间两个数值的平均数作为这些跳高运动员成绩的中位数,这是不正确的,共有15名运动员,按成绩排序,跳高成绩排列第8(最中间)的运动员的成绩才是这些运动员成绩的中位数.
正解:跳高成绩排列第8的运动员的成绩为1.70m,所以这些运动员成绩的中位数为1.70m.
点评:将这组数据按大小顺序排列,处于最中间位置的一个数据(或最中间两个数据的平均数)就是这组数据的中位数,可知中位数不一定是数据中的数.还应注意中位数的单位与原数据的单位一致.
三、对众数的“众”理解不够
例3“只要人人都献出一点爱,世界将变成美好的人间”.在今年的“慈善一日捐”活动中,某中学八年级(2)班50名学生自发组织献爱心捐款活动.班长将捐款情况进行了统计,并绘制成了统计图.试根据下图提供的信息,确定捐款金额的众数.
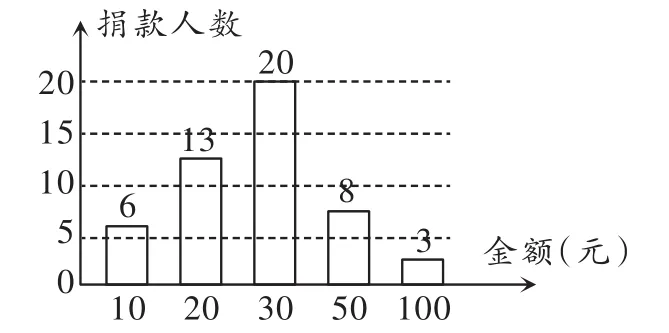
错解:众数为20.
剖析:错解以为捐款30元的人数最多为20人,所以众数就是20,把出现次数最多的数据的次数错以为是众数.这是对众数的“众”理解不够.
正解:从图中可以看出,捐款30元的人数最多,所以捐款金额的众数是30元.
点评:在确定众数时,易把出现次数最多的数据的次数错认为是众数.应注意众数是出现次数最多的数据,而不是出现的次数.一组数据的众数有时不止一个,当出现次数最多的数据是n个时,则这组数据的众数就有n个.众数的单位与原数据的单位一致.
四、对极差、方差的“差”理解不够
例4甲、乙两名射击运动员参加某大型运动会的预选赛,在相同条件下他们分别射击5次,甲命中的环数为:9,8,9,9,10;乙命中的环数为:7,10,9,10,9.如果甲、乙中只能有1人入选,你认为入选者应该是谁?为什么?
错解:入选的应该是甲.
根据题意,得
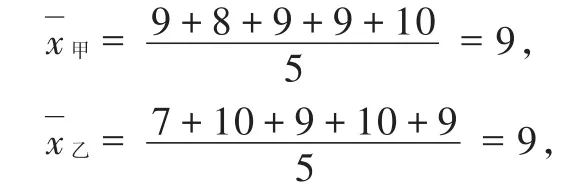
甲、乙两人的平均数相等,而甲的极差是2,乙的极差是3,所以入选的应该甲.
剖析:欲确定哪位选手,需判断哪位选手的射击成绩平均数大且较稳定,极差是指一组数据中最大数据与最小数据的差,它只能反映这组数据的变化范围,而方差才是用来衡量一组数据波动大小的统计量.
正解:入选的应该是甲.
根据题意,得
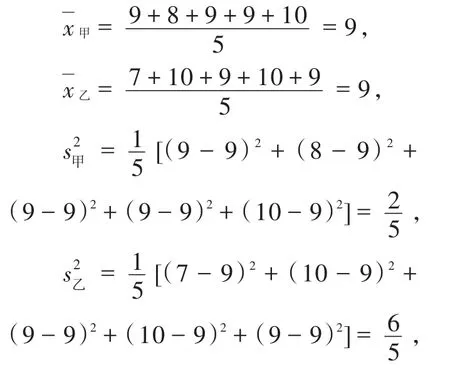
因为x甲=x乙,他们的平均数相同;而,甲的方差小于乙的方差,即甲的射击成绩比乙稳定些,所以入选的应该是甲.
点评:方差是刻画一组数据波动大小(离散程度)的重要量度.一般而言,一组数据的方差越小,这组数据就越稳定;两组数据中极差大的并不一定方差也大;极差、方差和标准差都有单位,其中极差和标准差的单位与已知数据的单位相同,使用时应当标明单位,方差的单位是已知数据单位的平方,使用时可以不标注单位.
五、对分类讨论的“类”理解不够
例5已知数据10、10、x、8的中位数与平均数相等,求这组数据的中位数.
错解:当x=8时,这组数据的中位数是9,平均数也是9,所以这组数据的中位数为9.
正解:(1)当x≤8时,该组数据从小到大顺序排列应为x、8、10、10,这时中位数为9,则,解得x=8,所以此时中位数为9;
(2)当8<x≤10时,该组数据从小到大顺序排列应为:8、x、10、10,这时中位数为,则,解得x=8,不在8<x≤10内,此时x不存在;
(3)当x≥10时,该组数据从小到大顺序排列应为:8、10、10、x,这时中位数为10,则,解得x=12,所以此时中位数为10.
综上所述,这组数据的中位数为9或10.
点评:分类讨论思想是初中数学中的重要思想方法,当问题可能出现多种情况时,要对可能出现的各种情况进行不遗漏、不重复的分类讨论,才能得出完整的结论.
