浅谈数列是函数
2016-06-29辽宁省锦州市太和区高级中学王曙光
辽宁省锦州市太和区高级中学 王曙光
我们在讲授人教B版必修五第二章第一节数列基本概念时,教材上是这样叙述的:从映射、函数的观点看,数列可以看作是一个定义域为正整数集 ( 或它的有限子集)的函数,当自变量从小到大依次取值时对应的一列函数值,而数列的通项公式也就是相应函数的解析式。实际上就是告诉我们,数列的实质是函数,理解好这一点,对于我们更好的把握数列这一概念,以及掌握解决数列有关问题的基本方法,会有很大帮助,现分析如下。
一、从数列定义看
按照一定的次序排列起来的一列数叫做数列。对于数列{an}每一项的序号n,在数列中都有唯一的一项an与之对应,序号n与这一项an的对应关系,符合映射的定义,实际上,可以看成序号集合到另一个数的集合的映射,因为是两个非空数集之间的映射,所以也是函数,因此从数列定义能够看出数列是函数。
二、从数列的表示方法看
数列的表示方法有三种,列表法、图像法、解析式法。例如,数列分别可以表示如下:
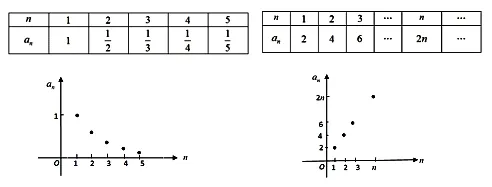
只是在用图像法表示数列时,注意数列的图像是一群孤立的点,这是数列这一函数的定义域决定的。另外用解析法表示数列时,不但可以用通项公式表示(就是函数的解析式),也可以用递推公式来表示数列。
三、从数列性质看
在讨论数列性质时,常常考察数列的最大(小)项是,数列的单调性,数列的周期性,数列项的符号的变化规律等等,这些性质都和函数的性质是一致的。
从以上几点,我们很清楚地感受到数列是函数,是一种特殊的函数这一事实。如果能从函数这一角度去看待数列,解决数列的有关问题,许多问题迎刃而解,很多方法就就会很容易想到和接受。
(一)函数中已知函数解析式,可实现自变量与函数值的互求,类似的数列中,已知通项公式,序号和项互求
例1.数列{an}的通项公式是an=3n-4,那么3n-1是数列的第几项?该数列的第2n项是什么?
分析:此题相当于函数中的已知解析式,然后函数值与自变量互求。
解:设am=3n−1 Qan=3n−4
∴ 3m−4=3n−1m=n+1
∴3n-1是数列的第n+1项 a2n=6n-4
例2.设数列{an}的第n+1项是n(n+1),求该数列的首相及通项公式。
分析:此题目相当于已知f(x+1)=x(x+1),求f(x). 可用换元法,也可以利用构造法。
解:法(1):(换元法)设m=n+1,则n=m-1, ∴am=n(n+1)=(m-1)m,∴an=n(n-1)∴a1=0
法(2):(构造法)∵an+1=n(n+1)=[(+1)-1](n+1) ∴am=n(n-1) ∴a1=0(二)函数中已知解析式还可以讨论函数的单调性、周期性及求最值。类似的数列也谈论这些性质,而且方法与函数一致
例3.数列的通项公式为它的前30项中最大项是第几项?最小项是第几项?
分析:此题可直接考查函数在(0,∞)上的单调性即可,方法完全是函数的方法。
解:
又∵n∈N+∴n≤9时 {an}递减,且an<1,当n≥10时,{an}递增,且an>1
∴当n=9时 an最小,当n=10时,an最大。
四、从等差和等比这两个特殊数列来看
等差数列若d≠0,则它的通项公式是一次函数,前n项和公式是没有常数项的二次函数,等比数列若q>0且q≠1,则它的通项公式及求和公式与指数函数有关系,解题时常可利用这个。
例4.等差数列{an}{bn}的前n项和分别为Sn、Tn,且
分析因为等差数列的前n项和是关于n的二次函数,且没有常数项,所以可分别把两个数列的前n项和设出,进而求解,当然也可以利用等差数列的性质来解。

此法利用等差数列的性质。
五、数列是函数,函数的问题也可借鉴数列的方法解决。
例5.已知函数f(x)=│x-1│+│x-2│+│x-3│+…+│x-20│,x
(1)分别计算f(1),f(5),f(20)的值。
(2)当x为何值时,f(x)取得最小值?最小值是多少?
因为自变量 ,所以考虑到可把看作 ,即可求解。
解:(1)
f(1)=│1-1│+│1-2│+…│1-20│=1+2+…+19=190
f(5)=│5-1│+│5-2│+…│5-20│=4+3+2+1+1…+15=130
f(20)=│20-1│+│20-2│+…│20-20│=19+18+…+1=190
(2)∵1≤9时,2x-20>0,当x=10时,2x-20=0,当x≥11时,2x-20>0时。
∴f(1)>f(2)>…>f(10)=f(11)
∴当x=1 0或1 1时,f(x)取得最小值,最小值为f(10)=f(11)=│10-1│+│10-2│+…│10-20│=9+8+7+…+1+1+2+…+10=100
综上所述,数列是函数,从这一角度去分析解决数列问题,很多问题都能自然的找到解决问题的途径和办法,因此在教学过程中,不要忽略对数列实质的挖掘,要重视数列就是函数这一事实的教学,以便拓宽我们的思路,把握问题实质。
