GPS并行频率域捕获算法分析
2016-06-29黄海生赵焕焕
黄海生, 张 伟, 赵焕焕
(西安邮电学院 电子工程学院, 陕西 西安 710121)
GPS并行频率域捕获算法分析
黄海生, 张伟, 赵焕焕
(西安邮电学院 电子工程学院, 陕西 西安 710121)
摘要:基于快速傅里叶变换的并行频率域捕获算法,建立该算法的数学模型。通过分析算法中频率步长的选择及快速傅里叶变换的栅栏效应对捕获精度的影响,给出捕获频率分辨率和功率相对损耗表达式,以此确定捕获配置参数。仿真结果表明,根据捕获配置参数,可以完成对全球定位系统信号载波多普勒频率的捕获。
关键词:全球定位系统;快速傅里叶变换;频率步进;频率分辨率
接收机是全球定位系统(GlobalPositioningSystem,GPS)的关键核心器件之一。通常GPS接收机先对卫星、CA码、多普勒频率进行三维搜索[1],即信号捕获,再将捕获结果中符合要求的信息牵入跟踪锁相环进行跟踪。
捕获算法主要有线性搜索、并行码相位搜索和并行频率域搜索3种[2-5]。线性搜索算法简单但搜索单元较多,搜索速度较慢[6];并行码相位搜索算法适用于信号的后处理,不适合在VLSI电路中实现[7];基于快速傅里叶变换(FastFourierTransform,FFT)的并行频率域捕获算法便于VLSI电路实现、部分电路可和跟踪环路复用[8],且在Matlab软件中的仿真速度也比较适宜[9]。
本文基于快速傅里叶变换的并行频率域捕获算法,建立算法数学模型;通过分析栅栏效应与频率步长对捕获结果的影响,计算由FFT栅栏效应与频率步长引起的捕获损耗,以期对随机信号进行捕获,确定捕获配置参数。
1并行频率域捕获算法与数学模型
1.1算法概述
基于FFT的并行频域搜索算法如图1所示。复信号经过复相位旋转下变频模块将频率降低,通过CA码相关器与分段积分模块解扩信号,得到的复信号等效于复正弦信号的采样点,最后复信号采样点经过FFT模块与取模平方模块,进行复FFT运算与取模平方运算。

图1 并行频率域捕获算法流程
1.2数学模型
中频输入的同相正交两路信号分别为Iin和Qin,则复信号为
Sin=Iin+jQin=ej(αt+φ0)。
(1)
式中α是信号输入信号角频率,t为时间,φ0是信号初始相位。
将Sin与本地信号SL进行复信号混频、相关、相干积分、FFT等操作,再将FFT结果取模平方。本地复正弦信号可表示为
SL=IL+jQL=ej(βt+φ1)。
(2)
式中β是信号SL角频率,t为时间,φ1为初始相位。
将Sin与SL进行复相位旋转下变频,混频结果为
[ej(αt+φ0)]*ej(βt+φ1)=ej(Δωt+φ)。
(3)
式中φ=φ1-φ0,Δω=β-α。
对Slow从时刻Tn到Tn+1进行积分得到信号

(4)
其中Ts=Tn+1-Tn。
信号S等价于对Slow以Ts为采样间隔进行等间隔采样,并且幅度缩小至sinc(ΔωTs/2),FFT运算就是对采样结果进行频谱分析。
2捕获参数分析
GPS导航数据位速率是50bps,无辅助捕获或冷启动情况下,截取数据长度不能大于10ms,以保证取连续两段数据至少有一段无导航数据跳变[10]。多普勒频率搜索范围为±5 000Hz,要求功率相对损耗小于2dB、频率捕获精度优于30Hz[12]。本文只分析无相位跳变的10ms信号,且CA码已经同步。截取10ms数据逐段进行1ms相干积分,得到10个积分结果,并进行补零FFT。通过分析栅栏效应、频率步长对捕获的影响,确定捕获配置参数。
2.1栅栏效应对捕获精度的影响
SL的傅里叶变换为2πδ(ω-Δω)。对SL截取时域长度为τ的数据等价于在时域乘以宽度为τ的门函数。信号截取后产生了频谱泄露,其带宽等于门函数的带宽4π/τ。
信号双边带宽与采样率的比值为

(5)
式中信号采样率fS=1/TS,M为时域采样点数,截取数据长度τ=M×TS。
由式(5)可知,fS不变,τ越长,频谱泄漏越小,能量越聚集。
对截取信号以TS进行等间隔采样得到的采样信号频谱为X(ejΩ),对应序列的傅里叶变换为X(ejω),其中ω=ΩTS。N点FFT是对X(ejω)在0~2π上进行N点等间隔采样得到X(k)(k=0,1,2,…,N-1),并且会产生栅栏效应。FFT模式有10-16、10-32、10-64和10-128共4种模式。以10-16FFT为例,其功率相对损耗如图2所示。
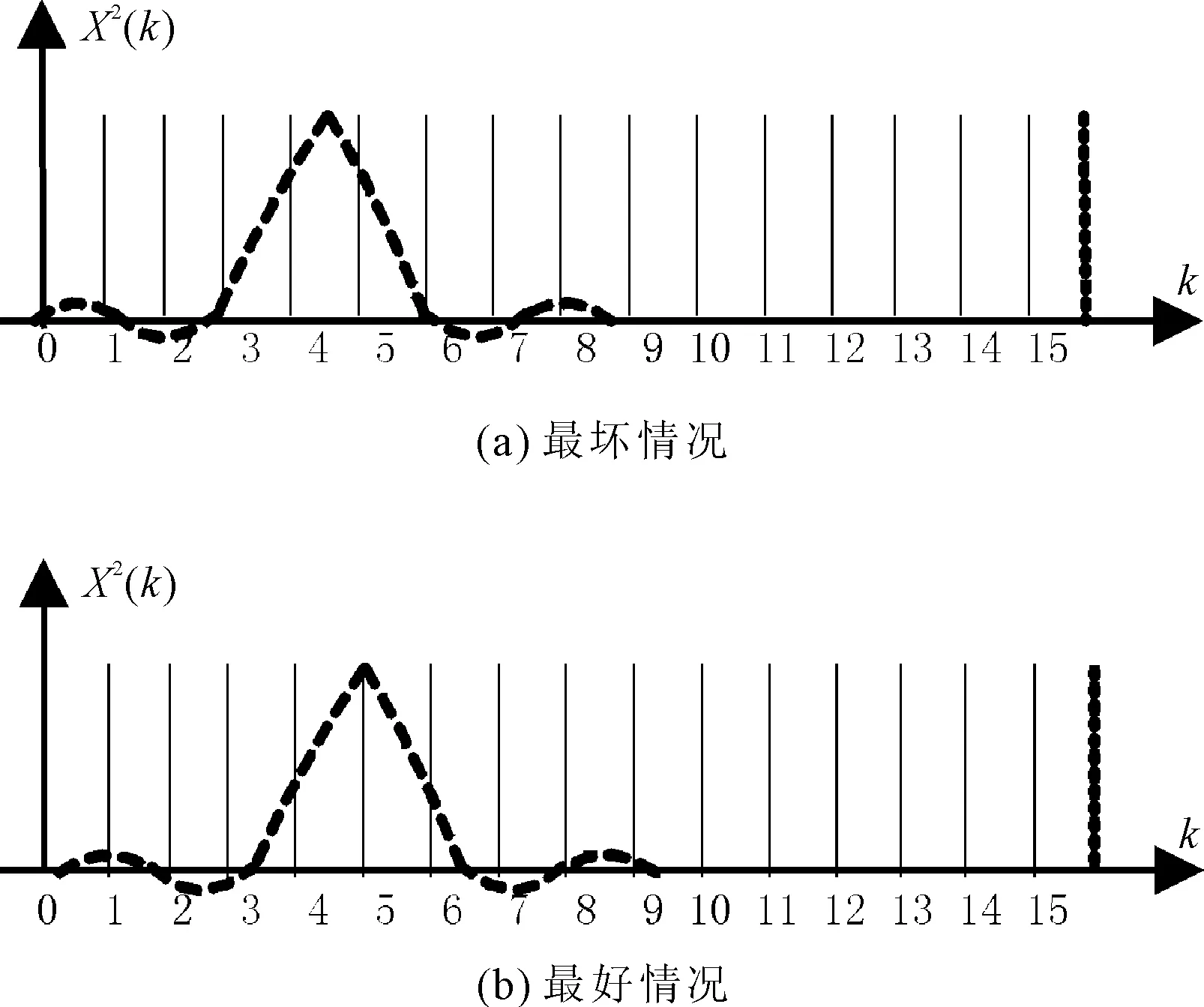
图2 10-16 FFT栅栏效应
FFT运算的频谱分辨率为
D=fS/N。
(6)
式中N为FFT点数。
频域带宽内的采样点数为信号双边带宽与频谱分辨率的比值,即

(7)
栅栏效应决定了频谱分辨率,同时还会导致频域采样值与频谱最大值相比有一定损耗。图2(a)所示最坏情况是信号S频谱峰值在两个采样点之间,功率相对损耗最大值为

(8)
图2(b)所示的最好情况是某个频域采样点恰在信号S频谱峰值,功率相对损耗最小,为零。由式(8)可知,补零FFT可以弱化栅栏效应,减小功率相对损耗、提高频谱分辨率,但会使运算量增加。
FFT点数是2的整数次幂,因此对10个1ms相干积分的结果必须进行补零FFT。补6个零进行10-16FFT,功率相对损耗最大值为1.443dB;10-32FFT最大损耗为0.352dB。10-64FFT的最大损耗为0.087dB。补零数量与采样点数相当时,进行FFT运算便可得到比较理想的效果。
补零FFT可以提高频率分辨率,依据式(6)可知10-16FFT与10-32FFT的频率分辨率分别为62.5Hz与31.25Hz,对应的捕获精度为31.25Hz与15.625Hz。不能仅依靠提高补零数量来提高捕获频率精度,因为当R较大时,频域各采样值相差不大,实际中加上噪声影响,很容易误判真实的信号频率。
FFT运算中补零越多越好,但当达到原采样点数2到3倍后,对弱化栅栏效应提升不大,而且运算量会急剧增长。
2.2频率步进对捕获精度的影响
相干积分长度要求至少小于正弦信号的半个周期,信号部分相关,等效的采样频率fS大于信号频率的两倍[11],否则不但会造成信号功率的降低,还会附加欠采样现象,将信号真实的频率造成未知量的降低。
由式(4)可知,信号功率因频率步长引起的功率相对损耗最大值

(9)
其中ΔF为频率步长,单位为Hz。
在限定的损耗下利用式(9)反推频率步长。频率步长越小,因混频结果不确定性范围造成的最大损耗越小。当相干积分为1ms时,各种频率步长因混频结果不确定范围引起的最大损耗如表1所示,结果截取均向上进位。

表1 各步长引起的最大损耗
由表1可知,当采样率大于信号频率两倍时,可将损耗控制在很小范围内,采样率继续增大对损耗影响不大。
2.3捕获配置参数的确定
总损耗被限定在2dB范围内。表2给出了各种FFT模式下,频率步长允许的最大损耗、对应的步长、捕获精度、带宽与频率分辨率比值等参数配置。
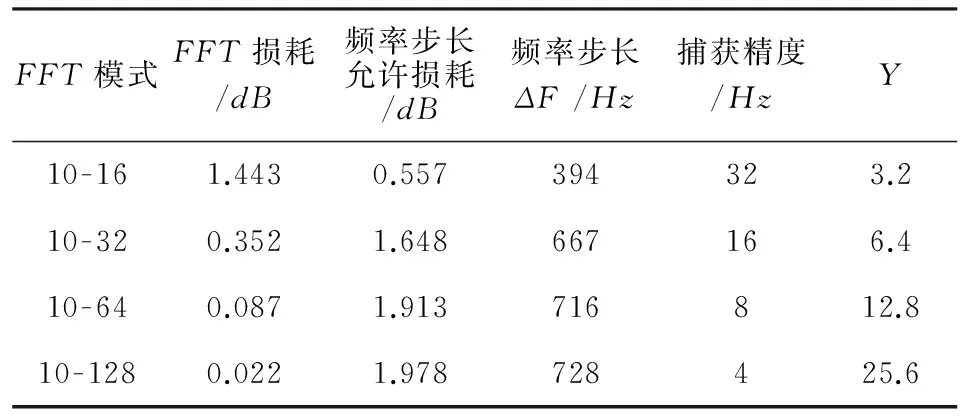
表2 各种参数配置
由表2可见,选择10-32FFT模式在运算量与性能方面是最好的权衡。
由多普勒搜索范围与频率步长可知所需的步进次数
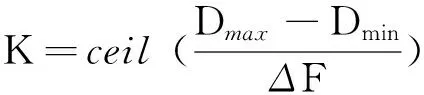
(10)
其中Dmax与Dmin分别为多普勒可能的最大值与最小值;ceil为向上取大于等于其参数的最小整数。
捕获中使用扫描模式对应的本地各频率值为
Fn=ΔF×(n-0.5)+Dmin。
(11)
其中n=1,2,…,K。
2.4FFT结果中频率的计算
找出各频率步进下FFT结果的最大值,依据该最大值所在位置计算Slow对应的频率值。
不考虑数据截取效应,信号Slow的频谱为2πδ(ω-Δω)。在满足采样率大于频率步进,即混频结果小于采样率一半的情况下,当Δω为正时,频谱冲击在频谱图的正半轴,FFT结果最大值在左半部分,为正频率;当Δω为负时,频谱冲击在频谱图的负半轴,FFT结果最大值是真实频谱以采样率向正轴搬移得到的,位于右半部分。
如果捕获峰值在FFT结果左半部分,则捕获频率为捕获峰值对应的本地频率直接加上FFT峰值代表的频率,反之,则需再减去采样率。
3实验结果
使用Matlab软件对捕获算法进行仿真。设中频信号Sin频率为96 250Hz,多普勒频率范围为-5 000~5 000Hz,采样率为1.023MHz。使用软件产生随机信号频率(含多普勒频率)为96 737.702Hz。当捕获配置参数TS为1ms、本地频率步进次数为1,且本地频率与待捕获频率相等时,进行混频差为零的10-128FFT捕获,结果如图3所示。

图3 混频差为零的10-128 FFT捕获结果
由图3可以看出,捕获结果峰值在FFT结果的第一点处,不会受栅栏效应影响。因此,最大值是信号频谱的真实峰值,将该峰值作为参考值,进行本地频率步进次数K为15次的10-128FFT模式捕获,结果如图4所示。其中X轴为各本地频点运算后的FFT结果;Y轴为本地各频点。图4对应的捕获配置参数TS为1ms,频率步进为667Hz,起始频率为91 583.5Hz,结束频率为101 588.5Hz,待捕获频率为96 737.702Hz。
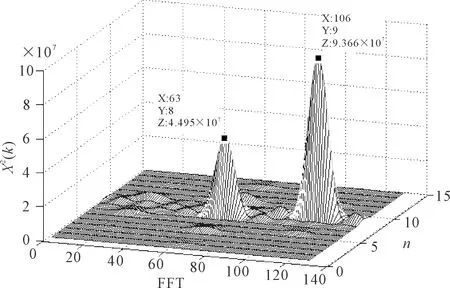
图4 10-128 FFT捕获
当本地频率为96 919.5Hz时,利用式(3)计算混频结果为181.8Hz,且小于fS/2,利用式(9)计算因频率步长导致的损耗为0.476dB。
由图4可知,最大值9.366相对图3的最大值10.470损耗了0.484dB,与计算值0.476dB基本一致。证明了式(9)的准确性。
由表2可知,10-128FFT模式因栅栏效应引起的功率相对损耗为0.022dB,可以忽略,因此,可将10-128FFT模式的捕获峰值近似为无栅栏效应频谱峰值。将图4中最大、次大峰值9.366与4.495作为参考值,进行10-32FFT捕获,结果如图5所示。
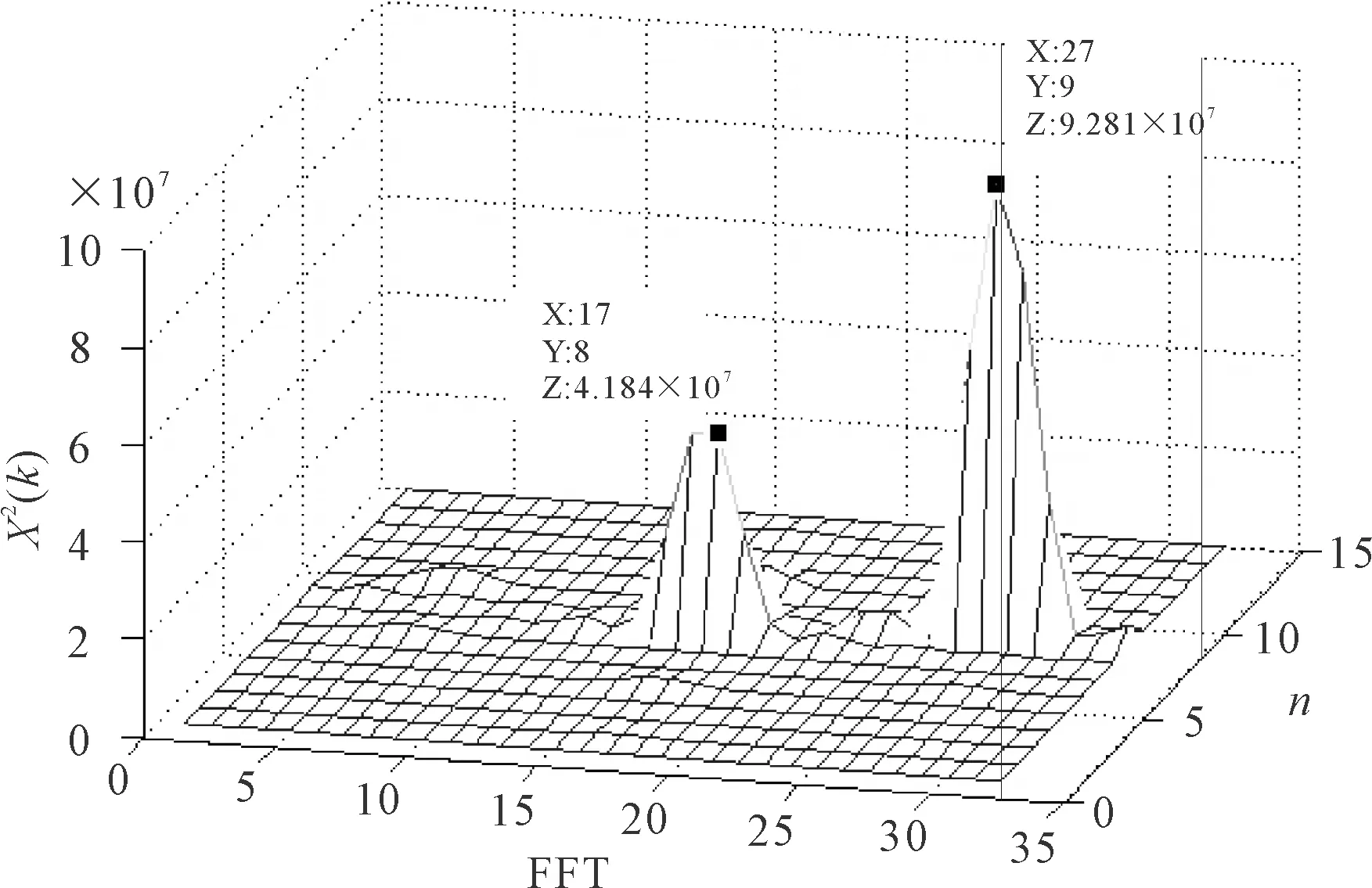
图5 10-32 FFT捕获
由图5可见,最大、次大峰值分别为9.281与4.184,相对于图4的峰值 9.366与4.495损耗不足0.040dB与0.311dB,小于表2给出的FFT损耗0.352dB,达到设计要求。
图5最大峰值出现在(27,9),即步进在第9步时峰值最大,代入式(10),频率为96 919.5Hz;峰值在FFT结果右半部分,因此,FFT结果代表负频率,值为-187.5Hz。最终捕获结果为96 732Hz,与96 737.702Hz相差-5.702Hz,与表2的16Hz相比,达到设计要求。
4结语
通过分析基于FFT的GPS频率并行捕获法中的主要参数对捕获功率与频率精度的影响,给出了捕获算法中频率搜索步数、本地信号各频率值以及FFT模式等捕获配置参数的计算方法。仿真结果表明,在给定的捕获频率分辨率与捕获功率损耗条件下,完成了对随机信号的捕获。捕获结果反映的参数与理论计算所得参数基本一致,并且,该捕获算法可以辨别FFT结果代表的频率正负性。
参考文献
[1]鲁豫.GPS全球定位接收机:原理与软件实现[M].北京:电子工业出版社,2009:47-49.
[2]赵丽.基于FPGA平台的GPS信号捕获算法研究与实现[D].南京:南京邮电大学,2012:13-17.
[3]吴娟丽.GPS软件接收机的研究及Matlab实现[D].西安:长安大学,2009:14-20.
[4]辛富国.GPS软件接收机捕获与跟踪技术研究[D].西安:西安电子科技大学,2011:25-30.
[5]苏丽娜.GNSS软件接收机捕获与跟踪模块设计和实现[D].镇江:江苏科技大学,2013:17-21.
[6]舒宇.GPS软件接收机基带处理算法研究与FPGA实现[D].哈尔滨:哈尔滨工程大学,2010:20-22.
[7]谢钢.GPS原理与接收机设计[M].北京:电子工业出版社,2009:372-374.
[8]张帆.GNSS单品软件接收机应用于编程[M].北京:国防工业出版社,2010:24-26.
[9]夏运兵,龚文斌,姜全江,等.GPS信号捕获算法Matlab/Simulink仿真[J].电子工程设计,2015,23(3):11-14.DOI:10.3969/j.issn.1674-6236.2015.03.005.
[10]TSUIJB-Y.FundamentalsofGlobalPositioningSystemReceiversAsoftwareApproach[M].HoboKen,NewJersey:AJOHNWILEY&SONS,INC.,PUBLICATION,2005:131-132.
[11] 易维勇,董绪荣,孟凡玉,等.GNSS单频软件接收机应用于编程[M].北京:国防工业出版社,2010:189.
[责任编辑:祝剑]
AnalysisonGPSparallelfrequencyacquisitionalgorithm
HUANGHaisheng,ZHANGWei,ZHAOHuanhuan
(SchoolofElectronicEngineering,Xi’anUniversityofPostsandTelecommunications,Xi’an710121,China)
Abstract:A mathematical model of Fast Fourier transform-based parallel frequency domain acquisition algorithm is proposed. By analysing the impact of acquisition accuracy caused by frequency step selection and fence effect of Fast Fourier Transform, calculation formula of acquisition frequency resolution and relative power loss are obtained to determine the acquisition configuration parameters. Simulation results show that the Doppler frequency of Global Positioning System signal can be acquired according to the acquisition configuration parameters.
Keywords:Global Positioning System , fast fourier fransform, frequency step, frequency resolution
doi:10.13682/j.issn.2095-6533.2016.03.005
收稿日期:2016-01-26
基金项目:国家科技重大专项资助项目(2013ZX02001010-003);陕西省科技统筹创新工程计划项目(2014KTCQ01-21);陕西省教育厅产业化培育资助项目(2013JC10)
作者简介:黄海生(1964-),男,硕士,教授,从事专用集成电路研究。E-mail:hhs@xupt.edu.cn 张伟(1990-),男,硕士研究生,研究方向为电路与系统。E-mail:1084020959@qq.com
中图分类号:TP961
文献标识码:A
文章编号:2095-6533(2016)03-0038-05
