Mathematica在以勒让德函数为基的广义Fourier级数展开中的应用*

程芳（长沙理工大学物理与电子科学学院，湖南长沙410004）



Mathematica在以勒让德函数为基的广义Fourier级数展开中的应用*

程芳
（长沙理工大学物理与电子科学学院，湖南长沙410004）

摘要：本文从广义Fourier级数展开教学着手研究，借助Mathematica的功能来实现以勒让德函数为基的广义Fourier级数的展开。将Mathematica应用于数学物理方法特殊函数以及广义傅里叶级数的教学中，可以使教学更加形象、生动，从而取得更加良好的教学效果。

关键词：Mathematica技术；勒让德函数；广义Fourier级数展开

Abstract：In this paper，we investigate how to apply Mathematica to expand of the generalized Fourier series based on Legendre's function. Mathematica can be of tremendous help in treating such problems and exhibiting their solutions graphically.The use of Mathematica can enhance the understanding of the generalized Fourier series.

Key words：Mathematica；laguerre polynomials；the expansion of the generalized Fourier series

Fourier级数是数学物理方法中的重要内容，同时也是其它后续课程的重要工具。广义傅里叶级数指勒让德函数、连带勒让德函数、贝赛尔函数等，它们与傅里叶级数一样都是一组正交完备的函数组，可以用于对函数的展开。广义傅里叶级数同样适用于求解微分方程，只是其适用的方程与连续傅里叶变换不同。Mathematica是当今世界上优秀的数学软件之一，它很好地结合了数值和符号计算、图形系统、编程语言，很多功能在相应领域内处于世界领先地位，且其界面友好，容易操作。

本文利用Mathemtica实现了函数的广义Fourier级数展开，将学生从繁重的手工计算中解脱出来，同时将抽象的理论与具体的图像演示结合，使学生能更深刻的理解函数展开成广义Fourier级数的基本概念和基本方法。

勒让德方程属于施图姆-刘维尔型方程，故其本征函数：勒让德多项式是完备的，可作为广义傅里叶级数展开的基。关于函数展开有下述定理：在区间［-1，1］上的任一连续函数，可展开为勒让德多项式的级数

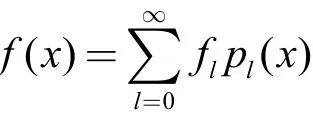
其中展开系数为

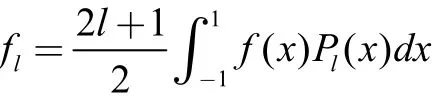
以勒让德多项式为基，Mathematica在广义Fourier级数分析中的应用。

例1：以勒让德多项式为基，在［-1，1］上，将f（x）=|x|展开为广义Fourier级数。

Mathematica程序代码如下：

Clear［f1，f2，f，L，Lmax，fu］

f［x_］：=Which［0＜x＜1，x，-1-x＜0，-x］；

f1=Simplify［（2L+1）/2*（Integrate［f［x］*LegendreP［L，x］，｛x，-1，1｝］），Assumptions→｛L/2∈Integers｝］

Lmax=Input［］；

f2=Table［（2L+1）/2*（Integrate［f［x］*LegendreP［L，x］，｛x，-1，1｝］），｛L，0，Lmax｝］；

fu［x_］：=f2.Table［LegendreP［L-1，x］，｛L，Length［f2］｝］

Plot［｛f［x］，fu［x］｝，｛x，-1，1｝，PlotStyle→｛RGBColor［1，0，0］，RGBColor［0，0，1］｝］

此程序的第1句给出了清除所有要使用的变量和函数的定义；第2句分段函数f（x）的定义；第3句是计算广义Fourier级数的展开系数的一般表达式；第4句将函数f（x）展开至广义Fourier级数的前Lmax阶；第5句函数f（x）的广义Fourier级数前Lmax阶的系数；第6句是计算前Lmax阶的广义Fourier级数；最后一句是将函数f（x）和函数f（x）广义Fourier级数的前Lmax阶两个图形显示在一起。运行上述程序可以得到：广义Fourier级数的展开系数（1+2 L）/（4 Gamma［3/ 2-L/2］Gamma［2+L/2］）

图1给出了函数的图形及其Fourier级数的前5阶、10阶和20阶对应的图形。从图1中可以清楚看出广义Fourier级数对函数的逼近效果：随着广义Fourier级数阶数的增加，其振幅越来越小，越来越接近要表示的函数。通过实例表明，利用Mathematica可直观地展示广义Fourier级数逼近函数，将抽象的问题形象化，从而化解了学生对广义Fourier级数表示函数理解上的困惑。

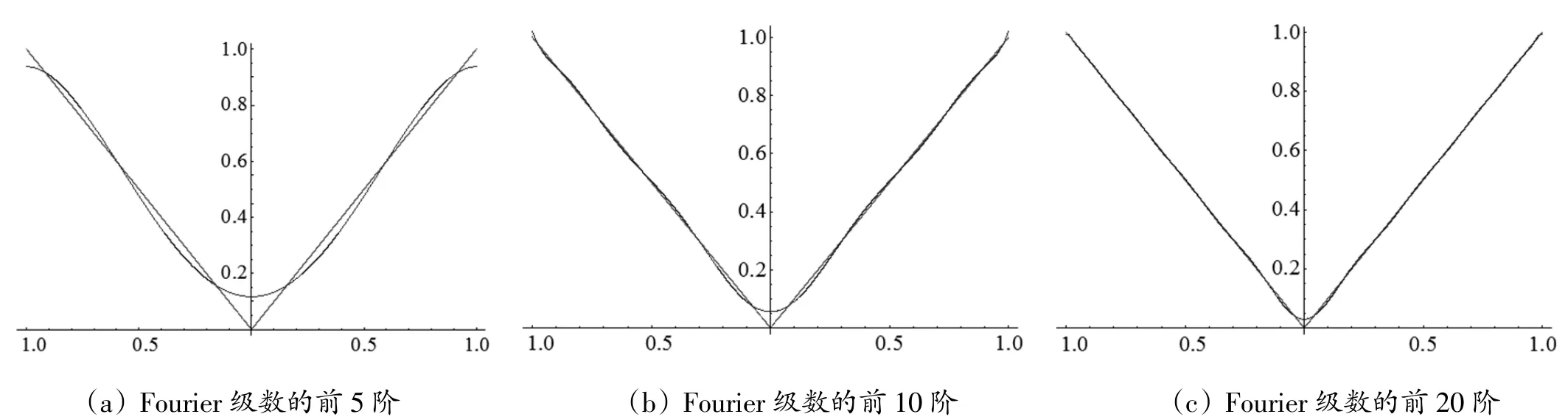
图1

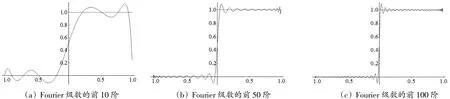
图2

我们知道，m相同的连带勒让德函数是完备的，也可作为广义傅里叶级数展开的基。关于函数展开有下述定理：在区间［-1，1］上的任一连续函数，可展开为广义傅里叶级数：

其中展开系数为

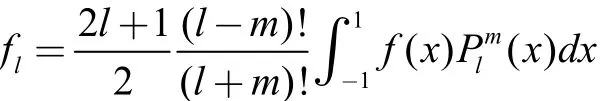
以勒让德函数为基，Mathematica在广义Fourier级数分析中的应用

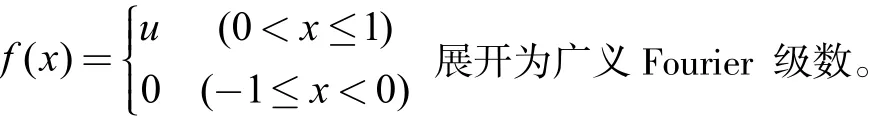
Mathematica程序代码如下：

Clear［ff，f，u，Lmax，fu］

f［x_］：=Which［0＜x？1，u，-1≤x＜0，0］；

Lmax=Input［］；

m=2；

u=1；

ff=Table［（2L+1）/2*（L-m）！/（L+m）！*（Integrate［f［x］*LegendreP ［L，m，x］，｛x，-1，1｝］），｛L，m，Lmax｝］；

fu［x_］：=ff.Table［LegendreP［L，m，x］，｛L，2，Length［ff］+1｝］

Plot［｛f［x］，fu［x］｝，｛x，-1，0.99｝，PlotStyle→｛RGBColor［1，0，0］，RGBColor［0，0，1］｝］

此程序的第1句给出了清除所有要使用的变量和函数的定义；第2句分段函数f（x）的定义；第3-5句分别定义广义Fourier级数参数l、m以及u的值；第6句将函数f（x）展开至广义Fourier级数的前Lmax阶的系数；第7句计算前Lmax阶广义Fourier级数；最后一句是将函数f（x）和函数f（x）广义Fourier级数的前Lmax阶两个图形显示在一起。

运行上述程序可以得到广义Fourier级数及其与原函数的对比图形。

图2给出了函数的图形及其广义Fourier级数的前10阶、50阶和100阶对应的图形。从图2中可以清楚看出广义Fourier级数对函数的逼近效果：随着广义Fourier级数阶数的增加，其振幅越来越小，越来越接近要表示的函数。

本文以勒让德函数为基讨论了Mathemtica软件在广义傅里叶级数分析中的应用。在广义Fourier级数教学中引入数学软件Mathemtica，从教学内容、教学形式、教学方法和手段上讲，都是对传统数学教学的一种发展和补充。在教学过程中，学生也从图形的变化、系数的计算等多方面对函数展开成广义Fourier级数进行学习，加深对抽象概念的感性认识，同时可以摆脱了繁琐的数学计算，使得问题简单化、可视化，从而达到逐步锻炼学生用数学理论、计算机知识来解决实际问题，提高了学生自主学习的积极性的效果。

参考文献

［1］阳明盛，林建华.Mathematica基础及数学软件［M］.大连：大连理工大学出版社，2003.

［2］梁昆淼.数学物理方法（第四版）［M］.高等教育出版社，2010.

［3］郭玉翠.数学物理方法简明教程（第一版）［M］.北京邮电大学出版社，2002.

中图分类号：G642

文献标志码：A

文章编号：2096-000X（2016）07-0067-02

*基金项目：教育部高等学校物理学类专业教学指导委员会教学研究项目“数学物理方法课程数字化教学的探索与实践”（JZW-14-SL-11）。

作者简介：程芳，女，汉族，中共党员，副教授，湖南省新世纪“121人才工程”第三层次人选，湖南省普通高校青年骨干教师。2008年获湖南师范大学凝聚态物理专业博士学位。2011年7月中国科学院半导体研究所博士后出站。自2008年参加工作以来，主持国家自然科学基金三项；湖南省自然科学基金重点项目一项；教育部项目一项；湖南省教育厅项目两项。主要研究介观系统的输运性质，近几年在国内外权威学术刊物如NewJPhys.、Phys.Rev.B、Appl.Phys.Lett.、NanoscaleResLett.、SolidStateCommun.、J.Phys.Cond.Matt.等三十余篇，均被SCI收录。