军事工程抢修任务规划问题研究

2016-06-28何苗王强荀毅魏晓航

中国储运 2016年6期

文/何苗　王强　荀毅　魏晓航

军事工程抢修任务规划问题研究

文/何苗王强荀毅魏晓航

摘要：本文针对战时军事工程抢修问题，研究在抢修资源有限的情况下，如何科学合理地安排抢修活动，最大限度恢复军事工程防护能力。通过引入抢修时间窗，同时考虑军事工程抢修的时间约束和逻辑约束，建立了使军事工程防护能力恢复最大的抢修任务规划优化模型，设计了一种离散型粒子群算法对模型求解。最后，以战场军事工程抢修任务为背景，用算例验证了模型的实用性和算法的有效性。

关键词：军事工程抢修；任务规划；时间窗；离散粒子群算法

现代信息化战争中，广泛应用高新技术，特别是精确制导武器和激光、隐形技术的发展和普及，使得军事侦察手段日益先进，武器系统命中率越来越高，破坏性越来越大。军事工程设施作为保障部队执行作战指挥、通信联络、后勤补给等任务的基本平台，是敌方攻击的首要目标。因此，如何快速抢修战损的军事工程，尽快恢复其保障能力，是赢得未来战争主动权的关键。在战争中，军事工程抢修最重要的特点就是时效性，要求使用一切可以利用的抢修资源，在尽可能短的时间内，对军事工程的毁伤部分进行修缮加固，使之恢复防护能力，抵御敌军武器系统攻击。军事工程抢修任务具有不同的技术特点，同时，各抢修分队力量构成存在着差异，抢修资源有限，不同抢修分队完成同一抢修任务的时间不同。因此，抢修资源优化配置对尽可能完成更多的军事工程抢修任务，最大限度恢复军事工作在作战体系中的保障能力具有显著影响，军事工程抢修任务规划问题也就成了一个需要研究解决的问题。

目前，对军事工程战损评估、抢修组织实施和抢修装备技术等方面均已有深入研究［1～3］。但是在军事工程抢修资源配置和抢修任务规划问题方面的研究甚少。关于抢修任务规划调度问题的研究，主要针对战场装备抢修及应急资源调度问题，建立基于排队论的数学模型［4］、多需求点多资源的二层优化调度模型［5］、非线性规划模型［6］，采用蚁群算法［7］、遗传算法［8］、蜂群算法［9］等优化算法对问题进行求解，为军事工程抢修任务规划问题的研究提供了新的思路和方法。本文将针对军事工程抢修任务规划问题的特殊性，建立抢修任务规划模型，并采用一种离散粒子群算法对该模型进行求解。

1.军事工程抢修任务规划模型

1.1问题描述

军事工程抢修任务规划是根据战场态势和军事工程战损评估结果，确定军事工程抢修目标任务的抢修时间窗口及所需抢修资源。针对每一个军事工程抢修项目，结合战区内的工程保障力量，科学合理地组织抢修资源，组建工程抢修分队，在军事工程抢修任务要求的时间窗口内及时做好抢修工作，最大限度恢复军事工程防护能力。

军事工程抢修任务规划问题可以描述为：在某一战斗区域内有M个军事工程抢修保障单位，每个单位有不同的保障资源，可以组成一个应急工程抢修分队。经现场调查评估，结合战场态势，认定共有N个军事工程受到敌方攻击受损，急需通过工程保障力量修缮恢复其防护能力。由于工程类别以及受损程度各异，同时，各个抢修分队力量构成不同，致使不同抢修分队完成同一工程抢修任务的时间不同。另外，由于各个军事工程在整个作战体系中的地位作用差异以及战场态势的不同，各个抢修任务必须在一定时间范围内执行，即任务时间窗约束。

1.2模型建立

设定军事工程抢修任务集合N={1,2,L，n }，n为抢修任务数目，∀j∈ N，[tsj,tej]为其抢修时间窗，tsj为其允许抢修的最早开始时刻，tej为其允许抢修的最晚结束时刻。Tj表示某个军事工程抢修分队开始对目标工程j进行抢修的开始时刻。∀k∈ N，pk表示军事工程k的任务优先级，也可以认为是军事工程k在整个作战体系中的重要性指标。

军事工程抢修分队集合为M={1,2，L m}，m为抢修分队的数目。∀j∈ N，∀i∈ M，tij表示抢修分队i对军事工程j进行抢修的时间长度。抢修任务目标之间的线路为：，t d k j表示某一抢修分队沿线路(k， j)转移的时间。抢修分队与抢修任务目标之间的线路为：。tdik表示抢修分队i从驻地出发，沿线路转移到任务目标(i， k)的时间。

综上所述，可建立该问题的数学模型，目标函数：

由于资源的有限性及抢修任务的多样性，目标函数设定为完成军事工程抢修任务优先级之和最大。

约束条件：

（1）每个军事工程至多由一个抢修分队完成抢修一次（小于1意味着没有针对该军事工程进行抢修）：

（2）抢修分队对任务目标抢修的时间必须在时间窗范围内：

（3）每个抢修分队至少对一个军事工程完成抢修任务。

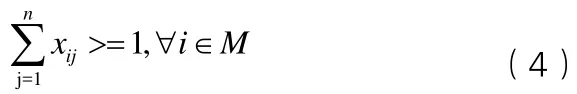
2.算法设计

2.1基本原理

粒子群优化算法（Particle Swarm Optimization， PSO）是由James Kennedy和Russell Eberhart于1955年提出的一种基于群智能的随机搜索算法［10］。基本粒子群算法的思想是模拟鸟群觅食的过程，将问题解空间中一个可行解看作一只鸟及所谓的“粒子”。这些鸟通过不停地改变自己的位置和速度去觅食，直到成功觅食（即最优解）［11］。基本粒子群算法所描述的粒子位置和速度都是连续变量，难以求解在离散空间中建模的任务调度问题。本文将采用一种适合军事工程抢修任务规划的离散粒子群算法。

2.2算法求解步骤

针对军事工程抢修任务规划问题，每个粒子代表一个可行解，即任务分配方案。用自然数对任务进行编码，粒子编码中的每一个自然数代表抢修分队，修任务数量为粒子编码长度。如图所示，有10个抢修任务，3个抢修分队。分队1负责任务3和任务5，其中任务2和任务9没有完成。得到一个粒子编码为（2，0，1，2，1，3，2，3，0，3）。

图1　离散粒子的编码方式

结合军事工程抢修任务规划问题的特点，本文采用式（5）分步计算和修改粒子位置，首先是当前粒子内部分量之间的交换，再根据粒子的历史最佳位置修改当前位置，然后根据粒子群体的最佳位置调整当前粒子位置。

其中，ω，c

，c

为扰动因子，其取值范围为[0,1]。函数

表示X

的第a个分量与第b个分量交换，a，b均为1到n之间的随机整数（a＞b）。并以c

为概率对位置交换进行扰动，

。

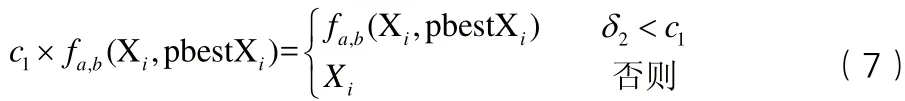
经过上述3个步骤，当前粒子位置调整完成，得到一个新解。利用DPSO算法求解的流程如图2所示。

图2　DPSO算法求解流程

3.算例

在某作战区域内，有10个军事工程抢修任务，分布在不同地里位置。共组建3个不同的工程抢修分队，它们从驻地到各个军事工程抢修任务点的转移时间如表1所示，抢修分队完成各个抢修任务的时间如表2所示，抢修分队在各个抢修任务点之间的转移时间如表3所示。各个抢修任务接受抢修的时间窗及任务优先级如表4所示。

利用DPSO算法对模型进行求解，设定种群规模为20，最大迭代次数为1000次，独立运行20次，目标函数值稳定在53，可得军事工程抢修任务方案如表5所示。由于时间约束的限制，抢修任务3、任务5和任务7未能完成。

4.结语

现代战争中，军事工程设施在体系对抗中具有重要作用，对战损军事工程组织实施抢修具有较强的时间限制，即要在规定时间范围内完成尽可能多的抢修任务，最大限度恢复军事工程体系对抗中的防护能力。本文研究了基于抢修时间窗的军事工程抢修任务规划问题，综合考虑抢修活动的时间约束和逻辑约束，建立了抢修任务规划模型，并利用DPSO算法求解。算例表明，该模型和算法能较好地解决军事工程抢修任务规划问题。