水平井变密度筛管配合盲管控流完井参数优化

李　伟，陈　阳，邹晓敏

(1.长江大学，湖北荆州 434023；2.中国石化胜利石油工程有限公司钻井工艺研究院)

水平井变密度筛管配合盲管控流完井参数优化

李伟1,2，陈阳2，邹晓敏2

(1.长江大学，湖北荆州 434023；2.中国石化胜利石油工程有限公司钻井工艺研究院)

摘要：为更好地达到底水油藏向水平井均衡供液效果，针对变密度筛管配合盲管控流完井技术，讨论了配套的控流参数优化方法，建立了描述控流过程的耦合模型，采用微元段法求解，考虑了控流完井管柱对耦合流动的各种影响，定量给出计算方案。实例计算表明，变密度筛管配合盲管控流完井技术对油井生产压差剖面调节幅度达到80%以上，流率分布剖面呈现出类似无限导流井筒水平井的特征，说明调节效果较好。变密度筛管节流作用使得水平井平均净生产压差降低，在实际情况允许的条件下可提高总生产压差保持产量。

关键词：底水油藏；水平井；变密度筛管；耦合模型

我国底水油藏数量多，储量丰富，除大量天然底水油藏外，随着油田进入二、三次开采，更多油藏开发特征不断趋向于底水类型。底水的存在给油井生产带来严重的产水问题，常常表现为出水见水早，无水采油期短，见水后含水率上升快甚至暴性水淹，导致油藏采收率降低，油田开采风险增大。采用水平井开采底水油藏有延缓底水脊进的作用，但常规完井方法延缓底水脊进效果非常有限[1]。普遍存在的问题是水平井跟端压差大，容易引起底水脊进过快并造成跟端过早见水，使得油井产量减小，寿命缩短。为实现油藏向水平井均衡供液，达到延缓底水脊进的目的，变密度筛管配合盲管控流完井技术已在国内有实际应用，但缺乏理论支撑，仍然无法保证控流效果，因此本文初步建立了配套的控流完井参数优化设计方法。

1变密度筛管配合盲管控流完井技术

变密度筛管配合盲管控流完井管柱如图1所示，筛管和盲管按照基本结构单元(由满足盲管-筛管比例的最小数量的盲管和筛管组成的管柱称为当前节流区段的基本结构单元，盲管-筛管比例简称盲筛比例)前后连接起来形成完井管柱下入裸眼水平井筒。水平井筒内管流沿程摩擦阻力使得水平生产段不同部位的生产压差不同，水平井跟端生产压差最大，容易导致底水从该部位突破。变密度筛管根据水力学原理，利用节流方法将较大部位的生产压差合理消耗一部分。筛管基管上孔眼的孔径和孔密都比普通筛管上的小很多，保证其能够起到节流作用。

在图1中，整个水平段内的筛管被分为5段，前4段为节流区段，每个区段的盲管与筛管比例不同，筛管的基管上孔眼参数也不同。越靠近水平井跟端，生产压差越大，需要人为消耗的压差也越大，为了起到预期的节流作用，该区段筛管的基管上孔眼数量越少，孔径相对越小，盲管比例越高，增加盲管比例，本质上也是起到控制孔眼数量的作用。越靠近水平井指端，变密度筛管节流作用越弱，对于第5个区段，则采用普通筛管，无需调节。

图1　变密度筛管配合盲管控流完井管柱

2耦合模型

2.1模型建立

以水平井水平生产段为研究对象，建立综合了油藏渗流和井筒管流的三维稳态耦合模型。设定流体为不可压缩符合做达西流动的单相原油，储层为各向异性的均质砂岩。模型采用微元段法求解，在油藏渗流模型中，水平井从逻辑上被分割为一个个线汇；在井筒管流模型中，水平井从逻辑上被分割成对应的一个个井筒段，在井筒中下入的完井筛管也同样被分割，所有计算过程都以线汇和井筒段为单位。在耦合模型中，油藏渗流和井筒管流在流压和流率两个层面相互作用，相互影响，最终达成稳态耦合流动，从数学上表达为对于任意位置经油藏渗流模型计算得到任一位置的流压与经井筒管流模型计算得到的相等，即模型的耦合条件，具体操作方法可通过节点法体现，如图2所示。

图2　节点示意

图2给出下入筛管后稳态耦合模型求解的直观景象，即从两个方向求解到当前井筒段解节点处的流压相等，其中求解方向1从油藏边界计算至解节点，代表油藏渗流压降，属油藏渗流模型；求解方向2从水平井跟端计算至解节点，代表井筒管流压降，属井筒管流模型。解节点在每个井筒段内设置一个，通过计算得到解节点的流压和流率，用来绘制水平井压差分布剖面和流率分布剖面，因此解节点是数据采集点。为了绘制出节流后的净生产压差(本文为表述方便，将扣除节流压降后的生产压差称为净生产压差)，解节点设置于紧贴完井管柱外壁的位置，节流压降由此规划到井筒管流模型中。下入控流完井管柱后的耦合模型，不能像普通耦合模型那样按照任一长度平均分段，而是应当按照单根筛管和盲管的长度分段，这样可使得模型逻辑运行机制和筛管实际结构的契合程度达到最佳，该长度通常是10 m。

根据以上思想可给出描述稳态耦合流动的数学模型。对于当前井筒段存在：

PH+ΔP2k=PW-ΔP1k

(1)

其中：

ΔP1k=ΔPMk+ΔPdk+ΔPGk

(2)

ΔP2k=ΔPFk+ΔPACCk+ΔPCk

(3)

式中：k——井筒段编号，k=1,2,3,…，对于水平井跟端的起始井筒段有k=1；PH——水平井跟端流压，MPa；PE——油藏边界压力，MPa；ΔP1k——油藏边界沿计算方向1到当前井筒段解节点的总压降，MPa；ΔP2k——当前井筒段解节点逆计算方向2至水平井跟端的总压降，MPa；ΔPMk——油藏边界到当前井筒段的理想渗流压降，MPa；ΔPdk——当前井筒段的钻完井污染带附加压降，MPa；ΔPGk——当前井筒段的完井筛管附加压降，MPa；ΔPFk——当前井筒段解节点至水平井跟端的沿程摩阻压降，MPa；ΔPACCk——当前井筒段解节点至水平井跟端的加速压降，MPa；ΔPCk——当前井筒段所在节流区段的节流压降，MPa。

2.2油藏渗流模型

由图2可知，油藏渗流模型包括理想渗流压降、钻完井污染带附加压降以及完井筛管附加压降三部分，即计算方向1含盖的内容，其中前两种压降在相关文献[2-5]已有探讨，不再赘述。完井筛管附加压降主要由防砂类筛管本身和井壁所夹环形空间的储层砂堆积层引起，非防砂类筛管可忽略该压降。当前井筒段的完井筛管附加压降由三部分组成，表达如下：

ΔPGk=ΔPSCRk+ΔPSRk+ΔPSAk

(4)

式中：ΔPSCRk——当前井筒段的完井筛管滤砂层附加压降，MPa；ΔPSRk——当前井筒段的流体沿储层砂堆积层径向渗流附加压降，MPa；ΔPSAk——当前井筒段的流体沿储层砂堆积层轴向渗流附加压降，MPa。

在实际计算中ΔPSCRk很小，可忽略。ΔPSCRk的计算方法表达如下[6]：

(5)

AS=2πRWLS

(6)

式中：ρo——原油密度，kg/m3；qk——当前井筒段的壁面流入流量，m3/d；μo——原油黏度，mPa·s；KG——筛管和井壁所夹环形空间的储层砂堆积层渗透率，μm2；LS——井筒段(线汇)的长度，m。

其余参数的含义及计算方法见参考文献6。ΔPSAk产生的原因是，如果当前井筒段内布置的是盲管，从井壁流入的流体必须在储层砂堆积层内沿井筒轴向运移到有筛管的位置，才能进入井筒，从而产生渗流附加压降；如果当前井筒段内布置的是筛管，该压降可忽略。为了简化计算，将单根筛管上所有孔眼在水力学上等效成一个孔眼，该等效孔眼布置于筛管中部，其流动过程如图3所示。

图3　储层砂堆积层轴向流动示意

值得注意的是，如果当前井筒段内布置的是盲管，那么从井壁流入的流体有可能向下游最近的筛管运移，也可能向上游最近的筛管运移，因此夹着盲管段的两个筛管之间必定存在一个分流界限，分流界限上下游相邻两个等效水力学孔眼所夹的井筒段称作当前分流界限的控制区域。分流界限的位置可由如下关系确定：

ΔPSADm+ΔPPEi=ΔPSAUm+ΔPPEi+1+ΔPWEm

(7)

(8)

(9)

式中：m——分流界限编号，m=1,2,3,…；i——水力学等效孔眼编号，i=1,2,3,…；ΔPSADm——由当前分流界限沿储层砂堆积层向下游的轴向渗流附加压降，MPa；ΔPSAUm——由当前分流界限沿储层砂堆积层向上游的轴向渗流附加压降，MPa；ΔPPEi——当前等效孔眼的节流附加压降，MPa；ΔPWFm——当前分流界限控制区域的井筒管流压降，MPa；XCm——当前分流界限所处的位置，m；AA——筛管和井壁所夹环形空间横截面积，m2；q(x)——井壁流入流率分布函数，m3/(d·m)，可按照插值法确定。

由于q(x)是被求函数，因此XCm由迭代计算确定。在实际操作中，为了简化计算，可认为同一节流区段内的ΔPPEi和ΔPPEi+1近似相等，因此在式(7)中能够相互约去。

可见ΔPSAk的计算与当前井筒段所处节流区间的盲筛比例布置方案紧密结合，按照图3中所举情况，其计算方法如下：

(10)

2.3井筒管流模型

井筒管流模型包括计算变质量流沿程摩阻压降、加速压降以及基管上孔眼节流压降。对于变质量流沿程摩阻压降和加速压降，相关文献已有报道[7-11]，不再赘述。这里只讨论对沿程摩阻压降的矫正和孔眼节流压降的计算方法。

2.3.1沿程摩阻压降矫正方法

在布置为筛管的井筒段，筛管自身结构对沿程管流状态有很大影响，其沿程摩阻压降与普通圆管的有很大差别，主要体现在以下两个方面：

(1)基管上孔眼的影响。完井筛管的基管上打有孔眼(割缝衬管则为缝眼)，因此改变了管壁绝对粗糙度[12]。在常规完井筛管尺寸范围内，其影响程度主要受孔密和孔径影响，孔密和孔径越大，管壁绝对粗糙度越大，与孔眼分布相位角和孔深(即基管壁厚)无关。该影响在图1中第5个区段最明显，在第1～4个节流区段基本可忽略。考虑孔眼影响后，各个井筒段的沿程水力摩阻系数计算方法表达如下：

(11)

式中：n——区段编号，n=1,2,3,…；λRk——考虑基管上孔眼影响后当前井筒段的沿程水力摩阻系数，小数；λOk——按普通圆管计算的当前井筒段沿程水力摩阻系数，小数；DPn——当前区段筛管基管上的孔眼直径，m；DI——完井筛管内径，m；SPFn——当前区段筛管基管上孔眼密度，孔/m；SC——孔眼密度基准常数，SC=39孔/m。

λR的表达式为隐式格式方程，可用牛顿法迭代求根。经实际计算，如果DPn=0.01 m，DFn=20孔/m，λR通常比λO高出15%左右。

(2)管壁存在质量交换的影响。对于生产井，油流经基管孔眼流入完井筛管内部，如果当前井筒段的井筒管流为层流，则管壁流入使得靠近管壁位置的轴向流速增量大于靠近筛管轴心位置的轴向流速增量，从而增加了沿程摩阻压降。如果当前井筒段的井筒管流为紊流，则管壁流入使得紊流边界扩张，紊流层内轴向流速增加，而紧靠管壁的层流边界层内轴向流速却减小，从而减小了沿程摩阻压降。

2.3.2孔眼节流压降计算方法

目前，针对孔眼压力降的计算一般采用实验曲线或经验公式确定，应用较多的是美国Esso公司的计算公式[13]。具体到本文模型，当前井筒段的孔眼节流压降以其所在节流区段为单位整体计算，计算方法表达如下：

(12)

Cdn=(1-e-0.866DPn×μ-0.1)0.4

(13)

式中：αn——当前节流区段的盲筛比例，无因次。

2.4耦合模型求解

建立水平井常规滤砂管完井条件下稳态耦合模型，利用微元段法求解。通过求解最终得到水平井井筒的生产压差分布剖面ΔPDP(x)和流率分布剖面q(x)，ΔPDP(x)将作为控流完井调节生产压差的参考基准。

确定控流完井管柱各个节流段的节流参数，细分为以下几个步骤：

(1)将整个生产段大致平均分为5段，前4段作为节流区段，其盲筛比α分别定为3，2，1，1/2。当然，根据具体情况可增加或减小区段的数目。当前节流区段长度必须为其基本结构单元的整数倍。

(2)获得各节流区段调节压差的意向值，计算方法表达如下：

(14)

式中：XBn——当前节流区段的起始位置，m，XB1=0；LCn——当前节流区段的长度，m；LT——水平生产段的长度，m。

(3)结合工程上成系列的基管孔径和孔密，逐个循环代入到式(12)和式(13)中，找到与ΔPEXn最匹配的SPFn和DPn，从而确定节流参数。

用微元段法求解耦合模型，细分为以下几个步骤：

(15)

(16)

式中：PH——水平井跟端流压，MPa，也是未知数；PE——油藏边界压力，MPa。

(4)判断迭代终点。如果相邻两组压力值以及相邻两组流量值的偏离程度满足精度要求，则计算结束，否则应再次迭代计算；

3设计实例

某水平井处于底水油藏中，其各项参数表述如下：油藏厚度20 m，油藏中部深度3 001 m，油水界面深度3 037 m，油藏压力32 MPa，油藏水平渗透率300×10-3μm2，油藏垂向渗透率199×10-3μm2，油藏孔隙度33%。原油黏度6.6 mPa·s，原油体积系数1.195，原油密度0.85 g/cm3，油藏底水密度1.1 g/cm3。水平井长度600 m，井眼直径165.1 mm，使用无固相清洁盐水钻井液，钻井液密度1.1 g/cm3，全井配产量500 m3/d。变密度筛管的防砂部分采用裸眼自洁防砂筛网，完井筛管外径127 mm，筛管基管外径101.6 mm，基管壁厚10 mm。将以上参数代入本文建立的耦合模型，得到控流完井方法和常规完井方法条件下生产压差剖面，如图4所示。

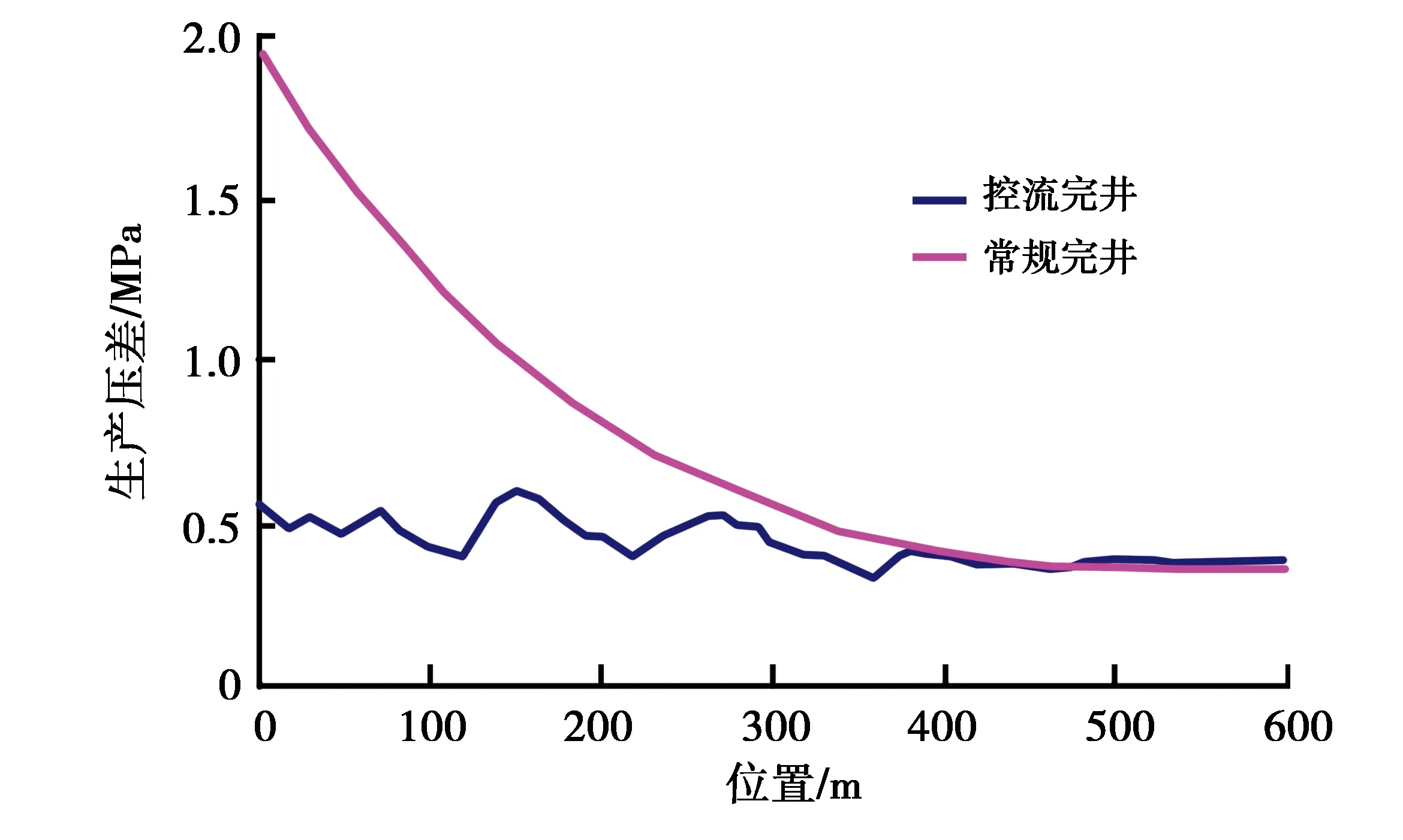
图4　两种完井方法条件下水平井生产压差剖面对比

由图4可知，常规滤砂管完井条件下水平井跟端和指端的生产压差相差达到1.6 MPa，如此大的差异极易导致底水从水平井跟端突破。控流完井管柱通过在不同部位适当节流，整个净生产压差剖面最大差值只有0.25 MPa。相比普通筛管，控流完井方法对生产压差的调节幅度达到84.4%，净生产压差剖面更加均衡(图5)。变密度筛管配合盲管控流完井参数如表1所示。

由图5可知，控流完井方法条件下流率分布剖面呈对称“U”形，类似于无限导流井筒，从而基本实现油藏向油井均衡供液。

符合工程标准系列规格的基管上孔眼的节流压降调节范围较广，最大可达3～4 MPa，因此水平井生产压差剖面越不均衡，尤其是高产井，变密度筛管节流作用对生产压差剖面的调节效果越明显。

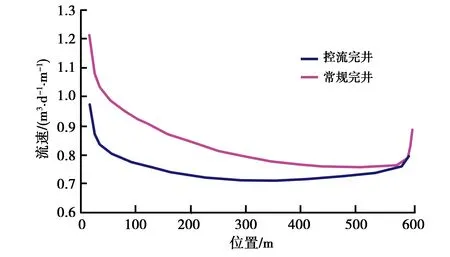
图5　两种完井方法条件下水平井流率分布剖面对比

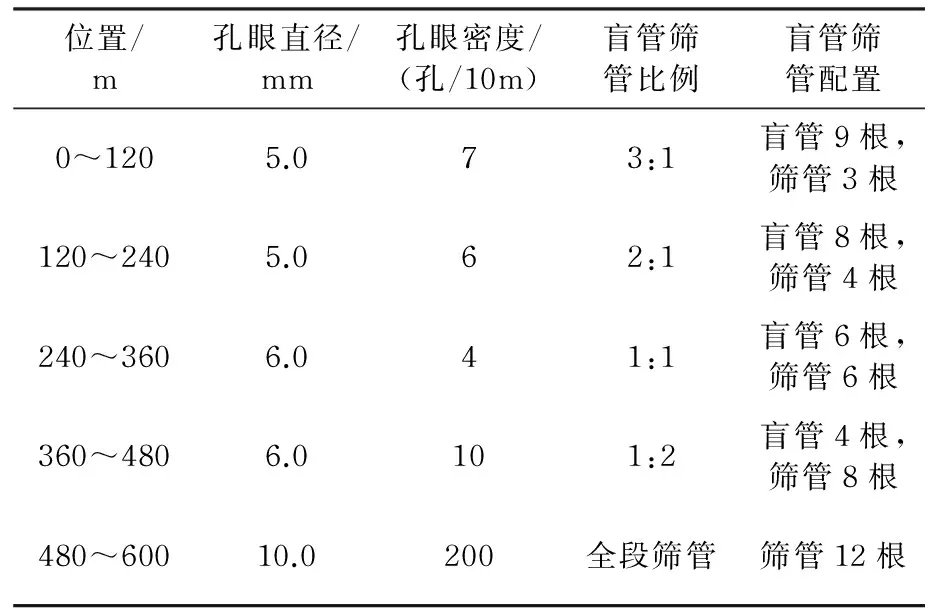
位置/m孔眼直径/mm孔眼密度/(孔/10m)盲管筛管比例盲管筛管配置0～1205.073:1盲管9根,筛管3根120～2405.062:1盲管8根,筛管4根240～3606.041:1盲管6根,筛管6根360～4806.0101:2盲管4根,筛管8根480～60010.0200全段筛管筛管12根

4结论与建议

(1)经控流参数优化设计后，变密度筛管配合盲管控流完井方法对水平油井生产压差剖面和流率分布剖面调节效果明显，基本达到均衡供液的要求；

(2)常规滤砂管完井条件水平井跟端生产压差较大，容易导致底水从跟端突破。为实现均衡供液，跟端部位变密度筛管节流作用较强，水平井生产压差剖面越不均衡，控流完井方法调节效果越好；

(3)变密度筛管节流作用使得整个水平井净生产压差降低，如果实际情况允许，可提高生产压差保持产量。

参考文献

[1]熊友明，罗东红，唐海雄，等．延缓和控制底水锥进的水平井完井新方法[J].西南石油大学学报(自然科学版)，2009，31(1)：103-106.

[2]Yildiz T. Multilateral horizontal well productivity[C]//SPE Europec/EAGE Annual Conference. Society of Petroleum Engineers, 2005.

[3]Ouyang L B, Aziz K. A general single-phase wellbore/reservoir coupling model for multilateral wells[J].SPE Reservoir Evaluation and Engineering, 2008, 4(4): 327-335.

[4]Fetkovich M D, Petrosky G, Hughesman C B, et al. Rate-time flow behavior of heavy-oil petrozuata field from multilaterals[C]//SPE/DOE Symposium on Improved Oil Recovery. Society of Petroleum Engineers, 2009.

[5]Tabatabaei M, Ghalambor A. A new method to predict performance of horizontal and multilateral wells[D].University of Louisiana at Lafayette, 2010.

[6]熊友明，潘迎德．裸眼系列完井方式下水平井产能预测研究[J].西南石油学院学报，1996，18(2)：42-46.

[7]Dikken B J. Pressure drop in horizontal wells and its effect on production performance[J].Journal of Petroleum Technology, 1990, 42(11): 1,426-1,433.

[8]Ozkan E, Sarica C, Haci M. Influence of pressure drop along the wellbore on horizontal-well productivity[J].SPE Journal, 1999, 4(3): 288-301.

[9]Novy R A. Pressure drops in horizontal wells: when can they be ignored[J].SPE Reservoir Engineering, 2005, 10(1)：310-318.

[10]Ozkan E, Sarica C, Haciislamoglu M, et al. Effect of conductivity on horizontal well pressure behavior[J].SPE Advanced Technology Series, 2009, 3(1): 85-94.

[11]Rodriguez O M H, Oliemans R V A. Experimental study on oil-water flow in horizontal and slightly inclined pipes[J].International Journal of Multiphase Flow, 2012, 32(3): 323-343.

[12]Su Z, Gudmundsson J S. Friction factor of perforation roughness in pipes[C]//SPE Annual Technical Conference and Exhibition. Society of Petroleum Engineers, 2006.

[13]万仁溥．采油工程技术手册[M].北京：石油工业出版社，2001：125-136.

编辑：李金华

文章编号：1673-8217(2016)01-0110-04

收稿日期：2015-09-30

作者简介：李伟，工程师，1985年生，2008年毕业于西南石油大学石油工程专业，现主要从事完井科研工作。

基金项目：国家科技重大专项“低渗油气田完井关键技术”(2011ZX05022-006)部分研究成果。

中图分类号：TE357

文献标识码：A