混合可再生能源路灯照明系统优化设计
2016-06-25王剑楠潘文平何丽娜南京航空航天大学民航学院江苏南京206河海大学地球科学与工程学院江苏南京2006地理信息工程国家重点实验室陕西西安70054
王剑楠,潘文平,何丽娜,吴 奈(.南京航空航天大学民航学院,江苏南京206;2.河海大学地球科学与工程学院,江苏南京2006;3.地理信息工程国家重点实验室,陕西西安70054)
混合可再生能源路灯照明系统优化设计
王剑楠1,潘文平1,何丽娜2,3,吴奈1
(1.南京航空航天大学民航学院,江苏南京211106;2.河海大学地球科学与工程学院,江苏南京210016;3.地理信息工程国家重点实验室,陕西西安710054)
摘要:商业用的独立照明系统一般是基于传统光伏电池和蓄电池配置而成。然而在远离赤道的地区无法满足一整年的工作要求。为了提高传统照明系统的实用性、经济性以及环保性,设计了一种由光伏电池、蓄电池组件和燃料电池组成的混合可再生能源系统来为路灯供电。在保证系统稳定可靠运行的同时,减少系统规模并尽可能降低成本是系统设计中的一个关键问题。为了减小系统的规模和成本,从能量管理的角度提出了一种解决该问题的新方法。建立了整个照明系统的仿真模型,通过定量分析确定了基于遗传算法的随机优化算法对整个系统成本进行优化,找出合理配置。使用的方法和结论可以为其他独立照明系统的设计提供帮助。
关键词:可再生能源;照明系统;燃料电池;遗传算法
路灯照明系统是一种必不可少的基础设施。城市中,已经有构建好的电网可以供路灯直接接入。而在一些偏远地区,因为其地理位置或基础设施建设等条件的限制,照明系统的设计与实现就显得非常困难。通常的解决方法是使用光伏发电与普通蓄电池相结合的独立照明系统[1-4]。然而,在远离赤道的地区,太阳能并不充足且太阳辐射量受季节变化的影响较大,这种方法并非一直有效。在太阳能短缺时(尤其是冬天),需要增加光伏面板的表面积和蓄电池的容量来满足照明所需电能。
为了解决这一问题,本文提出一种由光伏系统、蓄电池组件和质子交换膜燃料电池(PEMFC)组成的混合照明系统。研究中,国外学者提出增加一台柴油发电机进行额外供电[5]。然而,这种办法在消耗额外能源的同时会排放大量的温室气体。在国内,周林基概述了一种风光互补照明系统[6],该系统通过控制器给蓄电池蓄能,当太阳能不足时,由风力发电系统补充。但这种方法只局限于风能资源充足的地区。考虑到环保性和实用性,使用可再生能源产生氢气的燃料电池作为附加供电系统是一种合适的方法。设计时,主要问题集中在系统各组件(光伏面板、蓄电池、燃料电池等)尺寸的选择,以及对整个系统配置成本的优化。而遗传算法在电源优化领域得到了广泛应用[7-8],它是实现系统尺寸全局最优的理想算法。
首先介绍混合可再生能源照明系统的设计结构,构建系统的仿真模型。然后对目标函数中各参数的影响进行定量分析,选择基于遗传算法的随机优化算法搜索系统最优配置。最后,讨论了优化结果并从能量的角度阐述了优化后系统的特性。
1 系统结构
1.1蓄电池
采用铅蓄电池作为太阳能电源系统的储能装置。由于蓄电池能量密度高、功率密度高、循环使用寿命长、充放电性能好以及价格便宜等特点[9],是光伏发电中理想的储能设备。通常,照明系统中的负载恒定,因而对电池的电流响应速度要求低。此外,蓄电池的重量对系统也无影响,其效率可达80%[10]。
1.2光源
大多数路灯采用的是高压气体放电灯,它们的平均寿命一般为12 000 h(少于3年)。本文选择的是LED灯,它具有超长寿命,可达100 000 h,而且十分节能(本文中PLED=60 W)、环保。随着制造能力的提高,LED灯的价格在不断降低。在实际情况中,还可以调暗LED灯的亮度来降低能耗。
1.3光伏电池
该照明系统中,每年光伏电池提供的电能大约为328.5 kWh(由公式1中得出)。路灯平均每天工作时间为12 h(光照为零时路灯打开)。以美国波特兰地区为例,该地区的太阳辐射年总量是1.2 MWh·m-2,需采用300 Wp的多晶硅太阳能电池,因而每个路灯使用的光伏面板的表面积至少为3m2。为了减小表面积,唯一的办法就是增加其他供电能源,采用混合能源的形式为路灯供电。这种情况假设电池产生足够的电能为路灯供电。实际上,考虑到季节性的天气因素,需要在夏季存储一部分电能以供冬季使用。

1.4电力变换器
需要3个DC-DC变换器。第1个变换器通过采用MPPT(最大功率点追踪)算法来找到PV最大功率;第2个通过负载控制电流流向;第3个变换器用来控制燃料电池的电流。对于整个照明系统,光伏面板是不能同LED直接相连,因为它们不会同时工作。本文假设每个变换器效率为100%。
1.5燃料电池
在太阳辐射微弱而照明需求较高的阶段,增加额外的供电电源显得十分必要。被广泛应用于分布式发电系统的质子交换膜燃料电池(PEMFC)[11]是一种合适的选择。它通过对氢气和氧气的电化学反应产生电能,是一种清洁、高效的绿色环保电源。商业化的PEMFC发电成本约为5(Ballard公司的Nexa FC)。储氢罐可放置于路灯杆内,更换频率不低于2年。
该系统结构如图1所示。燃料电池在冬季的某些紧急阶段工作。此时负载所需电能多(夜间时间长),而光伏发电量较少。当电池的荷电状态SOC处于较低水平(如30%),燃料电池工作为路灯供电。白天,路灯处于闭合状态时,FC和PV同时给蓄电池充电。考虑到FC的使用寿命,不能频繁地启动或停止。最后,当蓄电池达到充满状态,FC停止工作。

图1 混合系统模型Fig.1 Principle of the simulation
2 系统模型
2.1照明系统模型
提出了一种简单的混合照明系统模型,主要由光伏电池、蓄电池组件和燃料电池组成。能够从能量的角度准确评估系统配置。因而只考虑系统的功率和能耗,不考虑设备的电压和电流。
光伏发电模型可以看作是一个增益,将天气数据(太阳辐射)转化为电功率。增益Gpv由公式(2)给出。其中,APV是太阳能电池板表面积,m2;ηpv是太阳能电池阵列的效率。

蓄电池的模型可由公式(3)描述。Eb为蓄电池存储的电能;Pb d表示蓄电池放电功率;Pb c为蓄电池的充电功率。这个模型虽然比较简单,但足够描述蓄电池的状态。需要注意的是,若计算出的电能是负值(图4所示),则表示光伏系统的发电量小于消耗量,需要蓄电池组件贮存的电能作为补充。Eb的最小值即为全年累计最大亏欠量,在成本函数中被用来表示对不被采用方案的惩罚。

在照明系统中,燃料电池(FC)总是在同一运行点工作,即发出的功率是恒定的。因而,其工作效率也是恒定的。基于这个假设,燃料电池发出的电功率可以简化为由氢气产生的化学能功率的增益。故可由如下积分得到氢气的消耗量[12-13]:

燃料电池的工作和停止状态是由蓄电池的荷电状态(SOC)来决定的。当电池的SOC达到某个SOCmin,则FC开始工作;当蓄电池充电到电量某一高值SOCmax时,则FC停止运行。
整个系统的运行原理如图2所示。蓄电池的功率变化情况由公式(5)给出:


图2 仿真模型原理图Fig.2 Principle of the simulation model
2.2天气数据
采用真实的气象数据来仿真光伏面板实际运行状态。为此,选取了位于美国波特兰地区的太阳能电站2014年某时间段内每天5 min一个值的太阳能辐照度数据。图3为一个采样图。

图3 太阳辐射数据Fig.3 Insolation data
为了使建立的光伏发电模型更为准确,本文连续2年采用相同的气象数据进行仿真。以避免原电池的荷电状态(SOC)可能带来的影响;因此,第2年的仿真结果更为准确。
气象观测站对太阳辐射的观测数据有2个:水平面直接辐射(Idir h)和水平面散射辐射(Idif h),W·m-2。两者的总和就是水平面总辐射(Iglobal h)。水平面总辐射不能直接用于计算非水平放置的光伏电池阵列发出的电功率,需要对观测值进一步转化以适用于倾斜放置的光伏电池阵列。Idir h与当地的纬度(φ)、太阳赤纬角(δ)和PV倾斜角(β)相关[14]。δ是太阳辐射同地球赤道平面的夹角。由于地球自转轴和地球轨道平面之间的夹角几乎是不变的,因而太阳赤纬角δ随季节变化,其变化周期为一年,即地球的公转周期。按照库珀(Cooper)方程,赤纬角可得[15]:

式中:N为按天数顺序排列的积日。1月1日为0,2日为1,其余类推。
从水平面直射辐射转化到倾斜的光伏电池面板上的辐射值可如下表示:

太阳的散射部分比较复杂,水平面散射辐射是太阳辐射经过大气中的云、气体分子、尘埃等散射到地球水平面的辐射。可以看作是与地球表面正交的射线。因而,从水平面直射辐射转化到倾斜的光伏电池面板上的辐射值可表示为

光伏电池面板上获得的太阳总辐射(Iglobal i)即为Idif i与Idir i之和。同时,光伏电池面板产生的能量与Iglobal i成正比。
2.3成本函数
成本函数即为要求其最小值的目标函数,可以分成两个部分。第一部分取决于使用设备的参数(功率、容量等),各项目在系统寿命周期内的单位成本如表1所示。第二部分是惩罚函数,取决于蓄电池贮存的电能(见公式9)。电力变换器的成本相比于整体的成本可以忽略,在此不再加以考虑。


表1 系统中各项单位成本和寿命周期Tab.1 Unit cost and lifetime of element
光伏面板的使用寿命和整个系统的寿命(LT)相同。因而PV发电成本与其发出的功率直接相关,见公式(10),LTb表示蓄电池的使用寿命。蓄电池的成本也由其使用寿命所决定,由公式(11)表示:

如上所述,蓄电池模型中贮存的电能可能是负值。其亏损与计算出的全年累计最大亏欠量(Ebmin)或连续2个亏欠期之间的盈余量(Esurplus)有关。可以通过计算蓄电池2年内存储电能情况获得Ebmin和Esurplus,如图4所示。
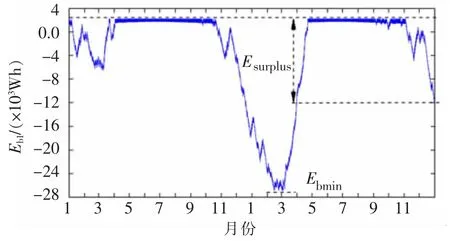
图4 两年内蓄电池存储电能的计算值Fig.4 Evolution of energy stored by battery over 2 years
公式(12)表示燃料电池总的成本,由燃料电池发电成本和消耗氢气的成本两部分构成。系统的工作寿命LT为25年,而燃料电池(FC)的使用寿命由它的工作时间和其工作开始与结束的循环次数决定。在系统的工作寿命内,所需的燃料电池数目NFC由公式(13)给出。

在遗传算法中,添加惩罚函数项是为了确保群体中具有一定数量的非可行解,使遗传算法从可行域和不可行域2个方向进行搜索,进而找到全局最优[16]。本文中的惩罚函数分为2种情况(见公式14)。第1种情况是系统正常工作,蓄电池容量Qb足够大。在这种情况下,惩罚值与一年内蓄电池电能的盈余量有关。实际上,如果存在盈余,意味着系统尺寸设计过大,应当减少光伏系统的发电功率,从而降低系统成本。
第2种情况是蓄电池容量不足,累积值Ebmin为负。此时,惩罚值主要由蓄电池的荷电状态SOC的最小值决定。而且,亏损依旧与第一种情况中的盈余量有关。
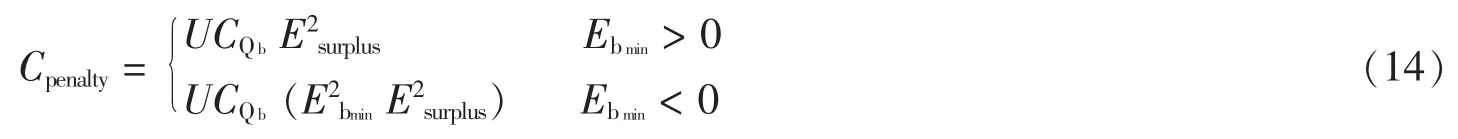
2.4仿真结果
仿真模型在Matlab软件中建立,模型中各参数初始设定如表2所示,仿真结果如图5所示。当FC不工作,白天光伏系统给蓄电池充电,晚上蓄电池以一个恒定功率放电。当蓄电池的SOC达到较低水平时,FC开始工作。光伏系统和燃料电池同时给蓄电池充电,直到SOC达到一个较高的值。根据仿真结果再对由公式(9)推导出的整个系统适应度进行计算。

表2 仿真模型中的参数Tab.2 Parameters of simulation model

图5 仿真结果Fig.5 Simulation results
3 优化设计
3.1问题构建
在设计街灯照明系统时,各个项目(PV,FC和蓄电池)的功率或容量必须事先确定。若只考虑一种供电电源的情况,所需优化参数减少,问题容易解决。当考虑了多种供电电源时,问题就变得复杂:每种电源的功率需要进行分析,还需要考虑每一项的价格及其寿命周期。在本优化问题中,由于PV的发电量取决于天气,因而目标函数同其余各项的参数并没有直接的联系。目标函数即成本函数由公式(9)给出。该问题可由如下公式化表示:在可行域D内找到等式(15)的解。

混合系统的可行域又由向量x中各参数的定义域所决定:

3.2初步分析
为了选择合适的优化算法,需要对成本函数中每一参数(见表2)的影响进行分析。选取某一个参数为变量,其余参数恒定,依次进行分析。根据该参数的变化作出成本函数变化图,以此选出对成本函数影响最大的参数。仿真结果如图6所示。图6显示了所有参数对于成本函数的影响。其中,Qb是对成本函数影响最大的参数,影响值超过5 000 S。别的参数也对成本有着重要影响,均超过1 000 S;因此,在优化过程中,所有的参数都需要考虑。

图6 各参数对成本函数的影响Fig. 6 Influence of the parameters on the cost function
图7是成本函数关于PPV和PFC两个变量影响时的图像。由于不连续,该函数是不可微函数。由图中可以看出,在系统的寿命周期内,参数LTCFC和LTHFC的燃料电池数目会对成本造成大幅影响。如果燃料电池的价格增加,数目的细微变化也会使得成本函数发生较大的跃迁;因此,不能采用梯度优化法进行优化。只有随机优化的方法适于找到目标函数的全局最小值。
此外,对成本函数的约束需要考虑PPV,PFC,Qb的局部最小值。若采用确定性算法不利用解决局部最小值问题。实际上,想要预测出带有6个参数优化问题的起始点非常困难。

图7 PV和FC对系统成本的影响Fig.7 Influence of PV and FC on the system cost

表3 于遗传算法优化参数设置Tab.3 Parameters settings for GA optimization
3.3采用遗传算法进行优化
基于最优化理论的遗传算法,常常被用来解决最优化问题,是一种全局搜索算法,可以找到最优化问题的精确或近似解[17]。本文采用基于遗传算法的随机优化搜索算法,通过在MATLAB软件中编程实现。该路灯照明系统的目标函数中6个优化参数的约束范围及操作参数设置如表3,表4所示。

表4 遗传算法操作参数设置Tab.4 Operation parameters settings for GA optimization

图8 参数进化图Fig.8 Parameters evolution

表5 参数个体最优值Tab.5 Parameters of the best individuals
4 结论
从能量管理的角度设计了一种带燃料电池的混合可再生能源路灯照明系统,无需考虑各个设备的电流电压,只考虑系统的功率和能耗。通过随机优化方法,找到适用于该照明系统中光伏组件和燃料电池配置的优化方法。最终,选择遗传算法确定了整个系统的最优配置,满足了合理的成本要求。本文所设计的优化方法,比通常人们的研究考虑了更多的优化参数,如光伏面板的倾斜角、燃料电池启动和停止的循环次数、蓄电池的SOC等。因而,该优化设计方法可应用于更为复杂的混合可再能源系统。未来的研究中,可以在该方法的基础上开发一种基于真实天气数据(风速、太阳能、负载曲线等)的软件,能够对各种复杂混合可再生能源系统进行更为智能的优化设计。
参考文献:
[1]董志明,常继彬,向李娟.太阳能驱动加油站LED照明系统优化设计[J].照明工程学报,2015,26(2):99-103.
[2]艾叶,刘廷章,王世松.独立式LED太阳能光伏照明系统的设计[J].电力电子技术,2010,44(2):18-19.
[3]鞠振河.太阳能路灯系统的优化设计[J].可再生能源,2007,25(5):79-83.
[4]陈尚伍,郑晟,翟建勇,等.太阳能照明系统的研究[J].照明工程学报,2006,17(4):60-62.
[5]DUIC N,CARVALHO M D G. Increasing renewable energy sources in island energy supply:case study Porto Santo[J]. Renewable & Sustainable Energy Reviews,2004,8(4):383-399.
[6]周林基.太阳能光伏照明系统概述[J].真空电子技术,2010(1):31-33.
[7]马艺玮,杨苹,吴捷,等.孤岛型混合可再生能源发电系统的优化设计[J].华南理工大学学报:自然科学版,2012,40(11):113-120.
[8]HUSSAINI MY,ABDULLAH MM,GRADY SA. Placement of wind turbines using genetic algorithms[J]. Renewable Energy,2005,30:259-70.
[9]林知明,魏九妹,刘珺.滞环PID控制在蓄电池充电器应用中的研究[J].华东交通大学学报,2014,31(5):93-98.
[10]MASTERS G M. Renewable and efficient electric power systems[M]//Renewable and Efficient Electric Power Systems. John Wiley & Sons Inc,2005:385-443.
[11]张丽彬,陈晓宁,吴文健,等.质子交换膜燃料电池发展前景探讨[J].农业工程技术·新能源产业,2011(4):15-19.
[12]LARMINIE J,DICKS A. Fuel cell systems explained[J]. Journal of Power Sources,2003,84(2):194-200.
[13]BLUNIER B,MIRAOUI A. Optimization and air supply management of a polymer electrolyte fuel cell[C]//Vehicle Power and Propulsion,2005 IEEE Conference. IEEE,2005.
[14]TIWARI G N,TIWARI G N. Solar energy:fundamentals,design,modeling and applications[M]. Pangbourne,England:CRC Press,2002:22-26.
[15]朱红路,李旭,姚建曦,等.基于非平稳太阳辐照强度计算和LMS滤波器光伏电站功率预测方法[J].可再生能源,2014,32 (6):765-769.
[16]张晶,翟鹏程,张本源.惩罚函数法在遗传算法处理约束问题中的应用[J].武汉理工大学学报,2002,24(2):56-59.
[17]薛定宇,陈阳.高等应用数学问题的MATLAB求解[M].北京:清华大学出版社,2008:381-388.
(责任编辑刘棉玲)
Optimal Design of Stand-alone Hybrid Street Lighting System with Fuel Cells
Wang Jiannan1,Pan Wenping1,He Lina2,3,Wu Nai1
(1.College of Civil Aviation,Nanjing University of Aeronautics and Astronautics;2. School of Earth Science and Engineering,Hohai University,Nanjing 210016,China;3. State Key Laboratory of Geo-information Engineering,Xi’an 710054,China)
Abstract:The commercialized stand-alone street lighting system based on the classical configuration coupling photovoltaic cells(PV)and battery cannot work all the year round in regions that are far from the equator. To improve the practicability,economy and environmental protection of the traditional system,this paper designs a kind of hybrid renewable energy street lighting system consisting of PV battery,storage battery and fuel battery to supply electricity for street lighting. It is significant to ensure the stable and reliable running of the system and at the same time reduce the system scale and cost. Therefore,this paper proposes a study of this problem by modeling the system from the perspective of energy management,chooses a genetic algorithm to design the hybrid system optimally and evaluates the validity of the design method. The proposed method can also help the design of other stand-alone lighting systems.
Key words:renewable energy;lighting systems;fuel cells;genetic algorithms
中图分类号:U491.5+3;TK519
文献标志码:A
文章编号:1005-0523(2016)02-0027-08
收稿日期:2015-09-05
基金项目:中央高校基本科研业务费专项资助项目(NS2015071);南京航空航天大学研究生创新基地(实验室)开放项目(kfjj20150709);南京航空航天大学青年创新项目(XAA15071)
作者简介:王剑楠(1990—),男,硕士研究生,研究方向为交通信息工程及控制,机场再生能源系统。
通讯作者:潘文平(1980—),男,讲师,博士,研究方向为航空电子电气测试技术,机载告警系统。
