基于超声传感器的胎心率检测优化算法*

黄新安

(江南大学 物联网工程学院，江苏 无锡 214122)

基于超声传感器的胎心率检测优化算法*

黄新安

(江南大学 物联网工程学院，江苏 无锡 214122)

摘要:获得胎心率信号的方法有多种，而以超声传感器检测法应用最广。然而如何在嵌入式实时系统中快速、准确地从含有噪声干扰的超声多普勒回波信号中提取胎心率信号成为一个难点。针对该难点，提出了一种基于经验模态分解(EMD)与提升小波变换相结合的去噪方法，再将去噪后的胎心信号采用希尔伯特变换提取信号包络，最后通过自相关运算得出胎心率。实验结果表明：采用这种方法能够有效提取到胎心率信号，使得胎心率计算耗时大大减少，同时，计算的准确性得到提高。

关键词:胎心率； 超声传感器； 经验模态分解； 提升小波变换； 自相关

0引言

利用超声多普勒技术测量胎心率是最常用的无创方法[1]。然而，超声多普勒胎心信号为非平稳信号，是生物医学信号的一种，其回波中含有各种干扰成分，如,母体心跳、胎儿在母体内的运动等。为了去除胎心音信号中的噪声，很多新的信号处理方法相继问世，国内外学者也针对各种方法提出了改进的算法。杨晓峰等人对小波阈值去噪方法的阈值和原始噪声方差的估计进行了研究，对阈值算子的系数进行改进能够自适应得到不同尺度上的去噪阈值[2]。赵继印等人根据多普勒胎心信号的特点，提出了基于coif5小波并采用双重阈值的胎心率提取算法[3]。但是这些算法计算时间比较长，不适合于嵌入式实时系统的要求。

提升小波变换既保持了传统小波的特性，又具有结构简单、运算快、存储空间少等优势而在高速处理、移动终端设备、低功耗设备信号的实时处理中应用前景广泛。然而，与传统的小波分析方法一样，提升小波变换的不足点就是需要事先选择特定的小波基，不具有自适应的信号分解特性。而基于经验模态分解(empiricalmodedecomposition,EMD)时频分析方法能够根据信号本身的特性进行自适应的时频分解，产生固有模态函数(intrinsicmodefunction,IMF)，分解后的IMF分量包含了信号从高到低的所有成分。EMD方法能够定量地描述频率和时间的关系，准确地刻画信号的非平稳特性，实现对时变信号的完整分析[4]。

本文结合EMD和提升小波变换方法的各自优点，提出了基于EMD的提升小波变换的胎心信号去噪方法。仿真结果表明，该算法得出的胎心率值耗时较少,且准确率高。

1EMD与提升小波阈值算法

1.1EMD算法

EMD方法将信号分解成有限个IMF分量。每个IMF必须满足两个条件：1)在整个数据段内，极值点的个数和过零点的个数相差小于等于1；2)在任意一段时间内，信号上包络线、下包络线确定的平均值为0[5]。对于给定的信号x(t)，EMD步骤如下[6]：

1)检测x(t)所有局部极大、极小值点，进而分别连接所有的局部极大、极小值点确定x(t)的上、下包络线,再取两条包络线的平均值组成新序列m(t)；

2)从x(t)中减去m(t)，得：h1(t)=x(t)-m(t)，如果h1(t)不满足条件1和条件2，则把h1(t)作为新的x(t)，重复步骤(1)和步骤(2)，直到循环k次后使得h1k(t)满足条件，记:c1(t)=h1k(t)；

3)从x(t)中分解出第一个基本模式分量c1(t)后，减去c1(t)，得到剩余值序列:r1(t)=x(t)-c1(t)；

4)将r1(t)作为新的原始信号重复上述操作，依次可得c2(t),c3(t),…cn(t)，最后分解剩余一项rn(t)。

经过EMD后任何复杂的信号均可以表示为

(1)

其中，分量c1(t),c2(t),…,cn(t)分别包含了信号从高到低不同频率段的成分，且随信号本身的变化而变化，很好地反映了信号任意时刻的局部频率特性。

为了使IMF分量尽可能多地反映频率调制和幅度调制情况，必须确定一个筛选停止准则。本文采用法国学者GabrielRilling提出的改进的停止准则[7]，即

(2)

图1为胎心音信号经EMD分解后得到的前6阶IMF分量。由图可知，前3阶IMF分量中含有的高频噪声较多。

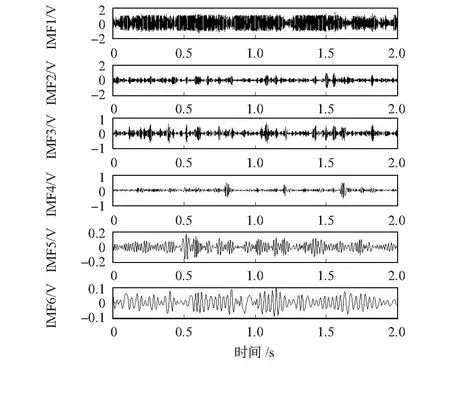
图1　胎心音信号的前6阶IMF分量Fig 1　The first six-order IMF components of fetal heart signal

1.2提升小波变换算法

信号都具有局部相关特性，所以,某一点的信号值可以由该点相邻的信号值通过适当的预测算子预测出来，预测出来所产生的误差就是高频信息，这就是预测环节。由预测环节得到的高频信息又通过更新算子来调整信号的下抽样得到低频信息，这个过程就是更新环节。实际上， 提升小波的核心就是更新算法和预测算法，通过预测算法可以得到高频信息，而通过更新算子可以得到正确的低频信息[8]。

信号的重构过程是分解过程的逆过程,即更新、预测、合并,并改变分解公式中的数据流方向和加减号即可得到。

与一般小波阈值去噪相同，提升小波变换信号去噪也是对小波分解的高频系数进行阈值量化处理达到信号去噪的目的，其中最关键的一步就是阈值的选取，直接关系到去噪的质量。DonohoDL等人提出了一种固定的阈值[9]

(3)

这种固定的阈值方法没有考虑到噪声方差在不同层数上的差异，实际上,阈值应该随着小波分解层数的增加而减小的。本文采用Birge-Massart算法来提取胎心信号分解成N层各层上的阈值。Birge-Massart算法是由j,M和ALPHA三个参数决定的。算法主要分为2个步骤：1)给定指定的分解层数j，保留j+1以及更高层的系数；2)对第i层(1≤i≤j)绝对值最大的ni个系数予以保存[10]，ni的表达式如下

ni=M(j+2-i)ALPHA

(4)

其中，M的默认值为L(1)，去噪时,ALPHA取3。

在阈值选取好后需要对小波系数进行阈值量化处理，阈值函数的选取就显得至关重要。常用的阈值函数主要有软阈值函数和硬阈值函数两种。但是硬阈值函数在阈值处不连续，软阈值函数重构信号与真实信号存在恒定的偏差。基于此，本文提出了一种改进的阈值函数，表达式如下

(5)

式中m为偶数。当|x|>λ时，随着m值的增大，阈值函数越来越接近为硬阈值函数。所以,可以用m来调节控制阈值化小波系数与原始小波系数两者之间的恒定偏差，使得重构得到的信号精度更高。通过大量实验验证，当m取4时胎心音信号滤波后的连续性和局部平滑效果较好。

1.3本文算法

信号经EMD后，得到时间尺度不同的IMF分量，这些IMF分量的频率几乎以2的负幂次方的形式从高到低顺序排列。噪声频率较高，一般在前几个IMF分量中。基于EMD时空尺度滤波算法简单地去掉1个或者多个IMF高频分量以实现滤波，将会丢失高频分量中含有的有用信号，使得重构信号失真。所以,需要对高频IMF分量进行滤波去噪，而提升小波阈值方法很适用于经EMD得到的这种时变的平稳的单分量信号[11]。结合两种方法的优势，本文提出了基于EMD与提升小波阈值的信号去噪算法。算法具体实现框图如图2所示。首先对胎心音信号进行EMD，对分解出的高频IMF分量(第1～m级)进行提升小波阈值处理，m一般取N/3。然后将处理后的IMF分量与未处理的低频IMF分量(第m+1～N级)进行叠加，重构增强后的胎心音信号。然后对重构后的胎心音信号进行希尔伯特变换提取信号包络，最后通过自相关算法来抑制噪声和获取胎心音信号周期从而得到胎心率值。

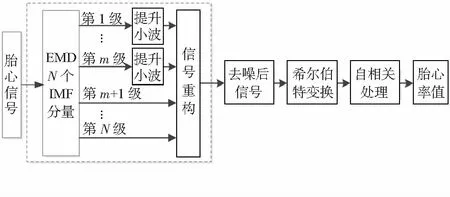
图2　胎心率优化算法过程Fig 2　Process of FHR optimization algorithm

2胎心率计算

为了能够更清楚地反映胎心音信号的特征，在计算胎心率之前采用希尔伯特变换提取信号的包络，之后对包络信号做自相关运算。对于实信号x(t)，其希尔伯特变换的定义为

(6)

则可以得到x(t)的解析信号为

(7)

则g(t)的模，即为原信号x(t)的包络。图3为一段胎心音信号经希尔伯特变换得到的信号包络图。

为了进一步提高胎心率计算的准确率，将提取得到的包络信号进行自相关处理，使得胎心音信号的周期更为明显。自相关表达式为

(8)

式中M为信号长度；n为相关函数长度；Rxx(n)为自相关函数值。为减少计算量采用欧洲标准，并由上式得到自相关处理后胎心信号的峰值位置值，求出胎心率。

图3　希尔伯特变换提取胎心音信号包络Fig 3　Extraction of fetal heart signal envelope based on HT

图4为胎心信号自相关函数图，可以得出最大峰值对应的序列号为814，所以,根据胎心率计算公式

(9)

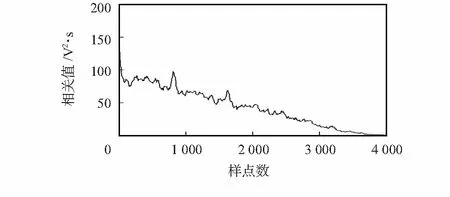
图4　胎心音信号自相关图Fig 4　Fetal heart signal autocorrelation figure

3实验结果分析

为了验证本文算法的有效性和实用性，追踪了20个孕妇，使用家用胎心仪定期采集一些实际的胎心音数据，组建成一个小型的胎心音数据库。选取胎心信号的采样率是影响胎心率计算的准确性的一个关键因素。若采样率太小，将导致胎心率在1min之内减慢或者加快，影响计算的准确性。胎心音信号最高频率成分一般为800Hz左右[12]，根据奈奎斯特抽样理论，抽样频率应大于1 600Hz，因此，本文提取胎心音数据时设定其采样频率为2 000Hz。

选取db6小波基，将1～3阶IMF分量分别进行三层分解，重构得到去噪后的IMF分量再与其他阶IMF分量进行叠加，得到图6所示的胎心信号波形图。通过与文献[2]中的算法得到如图5所示的去噪波形相比，EMD+提升小波阈值方法达到了较好的去噪效果，去噪后胎心信号的信噪比有较大的提高，得到的信号也较平滑。为了更加客观地看出本文算法的优越性，本文计算出了传统带通滤波器算法、文献[2]算法以及本文算法的平滑度r[13]，如表1所示，r越小，信号越平滑。平滑度公式为

(10)

图5　改进小波阈值去噪后胎心信号波形图Fig 5　Fetal heart signal waveform after de-noising based on improved wavelet threshold method

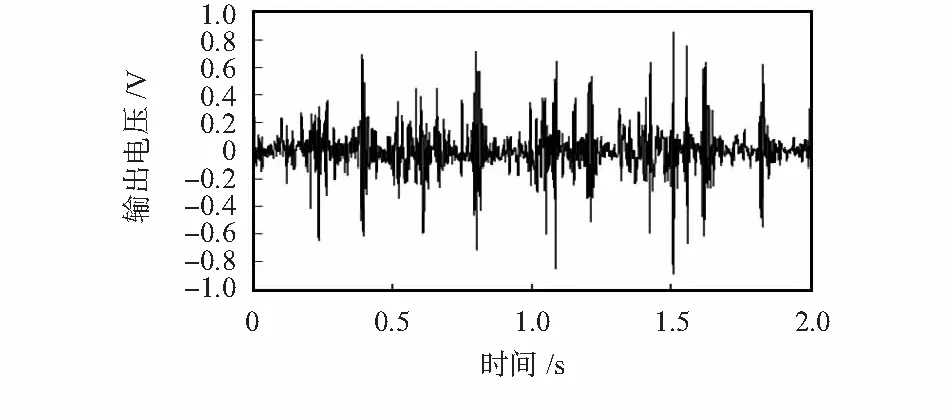
图6　本文算法去噪后胎心信号波形图Fig 6　Fetal heart signal waveform after de-noising based on proposed algorithm

算法带通滤波器文献[2]算法本文算法平滑度r0.00730.00610.0048

将胎心库中的160例胎心音分别采用本文算法和文献[2]中的算法进行信号滤波去噪处理，然后采用希尔伯特变换提取信号包络，最后通过自相关算法计算出胎心率，并与胎儿的临床状况进行了对比计算出不同算法得出的胎心率的准确率，得到如表2所示的胎心率监测结果。由表2可知，本文方法计算得出的胎心率的准确率最高。

表2　不同算法的胎心率监测结果

4结束语

本文通过对多普勒胎心回波信号的分析，结合EMD与提升小波的优势，提出了一种EMD与提升小波阈值相融合的多普勒胎心信号去噪方法，并在用希尔伯特变换提取包络信号后通过自相关算法计算出胎心率值。实验结果表明：采用该算法耗时比较少，能够有效抑制噪声和干扰，计算得出的胎心率值的准确率有所提高。通过大量临床实验验证，表明了该算法的有效性和实用性。

参考文献:

[1]袁飞.胎儿心率检测与非线性分析的研究[D].哈尔滨：哈尔滨理工大学，2009.

[2]杨晓峰，张欣，王金浦，等.基于小波变换的多普勒胎儿心率检测研究[J].西安交通大学学报，2007,41(8):917-921.

[3]赵继印，刘海英，马洪顺，等.基于Coif5小波的多普勒胎心音信号提取算法的研究[J].中国生物医学生物工程学报，2006,25(5)：538-541.

[4]宋知用.Matlab在语音信号分析与合成中的应用[M].北京:北京航空航天大学出版社,2013.

[5]唐贵基，向玲，朱永利.基于HHT的旋转机械油膜涡动和油膜振荡故障特征分析[J].中国电机工程学报,2008,28(2):77-81.

[6]李洋，景新幸，杨海燕.基于改进小波阈值和EMD的语音去噪方法[J].计算机工程与设计，2014,35(7):2462-2466.

[7]黄骏，何永勇.经验模态分解停止准则及在故障诊断中的应用[J].机械强度，2011,33(5)：655-659.

[8]Singh K K,Pandey R K,Suman S.Contrast enhancement using lifting wavelet transform[C]∥2014 International Conference on Control,Instrumentation,Communication and Computational Technologies (ICCICCT),IEEE,2014:447-451.

[9]Donoho D L.De-noising by soft-thresholding[J].IEEE Transactions on Information Theory,1995,41(3):613 - 627.

[10] 张德丰.Matlab小波分析[M].北京:机械工业出版社,2012.

[11] Patric Flandrin,Gabriel Rilling,Paulo Goncalves.Empirical mode decomposition as a filter bank[J].IEEE Signal Processing Letters,2004,11(2):112-114.

[12] 陈天华,韩力群,唐海滔,等.心音信号分析方法及应用性研究[J].北京工商大学学报:自然科学版,2009,27(2):35-39.

[13] 陈强，黄声享，王韦.小波去噪效果评价的另一指标[J].测绘信息工程，2008,33(5):13-14．

Optimizationalgorithmforfetalheartratedetectingbasedonultrasonicsensor*

HUANGXin-an

(SchoolofInternetofThingsEngineering,JiangnanUniversity,Wuxi214122,China)

Abstract:There are many ways to obtain FHR signal,and the most common way is to use ultrasonic sensor.However,it is a challenge to quickly and accurately extract pure fetal heart signal from Doppler fetal heart echo signal which has a lot of noise interference in embedded real time system.Considering the difficulty,a new kind of denoising method based on empirical mode decomposition (EMD) and lifting wavelet transform is constructed.Then use the Hilbert transform to extract envelope of signal and get fetal heart rate through autocorrelation operation.The experimental results show that the algorithm can effectively extract fetal heart rate signal,greatly reduce heart rate calculation time and improved veracity of calculation.

Key words:fetal heart rate(FHR); ultrasonic sensor; empirical mode decomposition(EMD); lifting wavelet transform; autocorrelation

DOI:10.13873/J.1000—9787(2016)04—0144—04

收稿日期：2015—07—25

*基金项目：国家自然科学基金资助项目(NSFC—ANR项目(中法))(61411136003)

中图分类号:TP 391

文献标识码:A

文章编号:1000—9787(2016)04—0144—04

作者简介:

黄新安(1990-)，男，安徽安庆人，硕士研究生，主要研究方向为生物医学信号处理。