基于伸缩梯度投影的天文图像复原改进算法
2016-06-24刘国良邵云龙
刘国良, 邵云龙
(桂林电子科技大学 信息与通信学院,广西 桂林 541004)
基于伸缩梯度投影的天文图像复原改进算法
刘国良, 邵云龙
(桂林电子科技大学 信息与通信学院,广西 桂林 541004)
摘要:在地基天文观测中,克服大气湍流造成的图像模糊是获取高分辨率天文图像的关键。反卷积是图像复原过程中的重要步骤,基于伸缩梯度投影的反卷积算法具有较高的复原精度和处理效率,且鲁棒性好,适用于天文图像的复原。但由于实际应用中清晰图像是未知的且存在噪声的干扰,该算法存在着无法自行停止迭代的弊端,限制了其应用。结合图像无参考质量度量给出一种可自动停止迭代的改进算法。仿真表明:改进的算法对最优点判断较为准确,能够运用于实际天文图像处理。
关键词:地基天文; 大气湍流; 伸缩梯度投影
0引言
在地基天文中,通过光学望远镜观测天文目标时必须穿过厚厚的大气层这一非均匀介质,使得观测图像因受到大气湍流的影响出现严重的模糊[1],影响了对目标的分析研究,因此,需要对天文观测图像进行复原。
图像反卷积是图像复原过程中的关键环节。目前经典的图像反卷积算法有:逆滤波[2]、维纳滤波[2]、约束最小二乘方滤波、Lucy-Richardson算法[3,4]等。维纳滤波算法计算量小,容易实现,但是需要图像的信噪比为前提。约束最小二乘方滤波与维纳滤波类似,在信噪比较高的情况下两者复原效果差不多,但在信噪比较低的情况下约束最小二乘方滤波更优。上述反卷积算法都是线性的,非线性反卷积算法中典型代表为Lucy-Richardson算法,是目前为止实际应用最为广泛的反卷积算法之一。BonettiniS等人提出了伸缩梯度投影[5](scaledgradientprojection,SGP) 算法,该算法具有精度高,对噪声鲁棒性好的特点。
SGP算法在仿真中可以根据原始清晰图像和每次迭代结果的对比作为一个度量来控制迭代算法的停止。实际中,由于没有原始清晰图像,加上噪声的干扰,使得无法控制SGP算法的停止。文献[6]给出了一种基于图像内容的图像质量评价因子并将其运用到去噪算法中,取得了不错的效果。文献[7]借鉴文献[6]的基本思路,提出了综合考虑噪声和模糊的无参考图像质量评价方法。文献[8]针对文献[6]中存在的问题提出一种改进的质量评价算法,该方法适用范围更广而且更为稳定,但具体实现比较困难。
本文根据问题背景,给出一种适用于天文图像的无参考质量度量并与SGP算法结合,并经过仿真验证了改进算法的有效性。
1伸缩梯度投影算法
通过将原始清晰图像f(x,y)∈Rn×n表示为一维向量x=[x1,…,xN]T,N=n2,图像的退化过程可通过下式表示
Ax+n=g
(1)
式中A为一个N×N的矩阵,泛指成像过程中成像路径对清晰图像的影响。x为估计结果,n指的是图像获取过程中的加性噪声,g为实际观测图像。根据非负性和通量守恒的约束,图像的复原问题可以转化为极小值问题
(2)
在SGP算法中,J(x)为Ax与g之间的K-L距离
J(x)=DKL(Ax,g)
(3)
为了加快收敛速率,SGP算法采取了有效的步长更新规则和伸缩策略。其中,伸缩矩阵Dk的更新规则为
(4)
(5)
式中L为一个合适的阈值。
文献[5]中详细地给出了步长αk更新规则。
经仿真分析:SGP算法在处理天文图像复原时效果比Lucy-Richardson算法更优。
2基于局部结构张量的图像质量度量
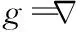
(6)
则点f(x,y)的局部梯度协方差矩阵可表示为
(7)
协方差矩阵SVD分解得到

(8)
式中U和V为正交矩阵,v1和v2分别为局部结构张量的主方向和次方向,特征值s1≥s2≥0,分别表示对应主方向和次方向上局部结构张量的能量大小。
根据局部结构张量的特征值,文献[9]、文献[10]分别给出如下反映图像局部结构的度量:
1)方向一致性度量:c1=(s1-s2)2;
s1和s2分别代表主方向和次方向的能量大小。对于度量c1:c1(边缘点)>c1(平滑区域中的点)≈0,即在图像的梯度变化大的区域,s1远远大于s2,在图像的平滑区域,s1≈s2≈0。c度量的是s1与s2之间的相对大小,对于度量c2:1≈c2(边缘点)>c2噪声点)≈0。
图1和图2分别给出了度量c1和c2在图像模糊程度变大和噪声水平变大的时候的表现。
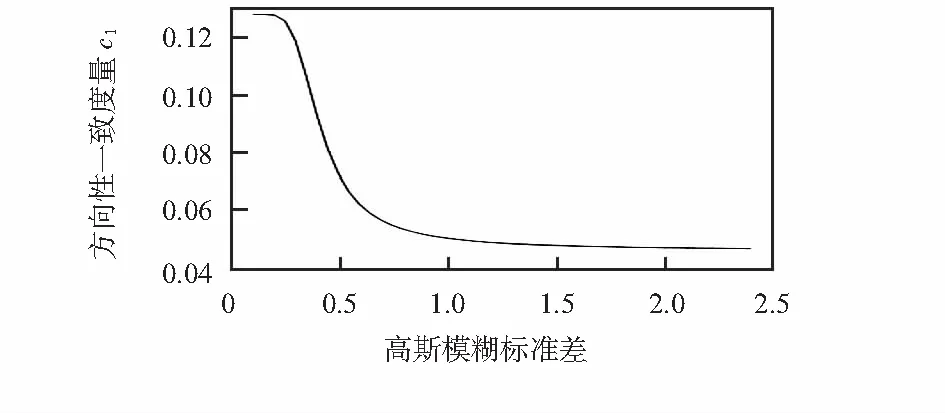
图1 度量c1跟随图像模糊度的变化情况Fig 1 Variation of c1 with image blur level change
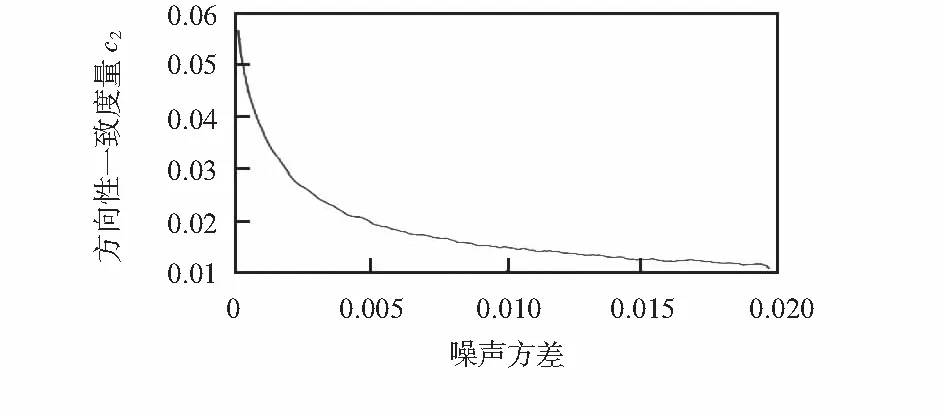
图2 度量c2跟随图像噪声水平的变化情况Fig 2 Variation of c2 with image noise level change
从图1和图2可以看出,随着图像模糊程度加剧,方向一致性度量c1越来越小,c2随着图像噪声水平增加而减小。因此,图像的c1值能有效表征模糊程度,c2值能有效表征图像的噪声水平。
结合问题背景,综合上述讨论和大量仿真,定义图像的质量度量为
(9)
图3和图4分别给出了上述质量度量在图像模糊度加剧和噪声水平变大时候的表现。

图3 度量Q跟随图像模糊度的变化情况Fig 3 Variation of Q with image blur level change

图4 度量Q跟随图像噪声水平的变化情况Fig 4 Variation of Q with image noise level change
从图3和图4可以看出:随着高斯模糊方差的不断增大,图像趋于模糊,相应的Q值不断减小。随着图像中噪声方差的不断增大,相应的Q值也不断减小。
在SGP算法的每次迭代时都计算一次Q值,随着图像的质量不断提高,Q值随之不断增加。当Q值变小的时候,停止迭代,即可得到估计图像。
3仿真结果与分析
用半径为13的高斯模糊算子将卫星图像模糊,然后加上一定高斯白噪声得到输入图像。在SGP算法中,每次迭代计算Q值的同时,计算均方误差MSE作为参照,仿真结果如图5所示。
为客观验证算法的复原质量,本文采用峰值信噪比(peaksignaltonoiseratio,PSNR)、均方误差(meansquareerror,MSE)、结构相似度(structuralsimilarity,SSIM)三个指标对复原结果进行评价。均方误差和峰值信噪比主要用于评价图像失真和噪声水平的标准,其定义分别为
(10)
(11)
SSIM是通过提取图像中的结构信息来评价图像之间的相似性,与前者相比,更接近人的主观评价[11]。

图5 改进的SGP算法的仿真结果Fig 5 Simulation results of improved SGP algorithm
分别给出退化图像,图5(e)和图5(f)的PSNR,MSE和SSIM指标,如表1所示。

表1 不同迭代位置复原图像的指标对比
上述实验中,由MSE和Q确定的迭代停止次数分别是23和24。从直观上看,两个位置的估计图像相比退化图像都极大地恢复了图像细节;从指标上看,改进算法的估计结果相比退化图像有了很大提高,且与最优点指标较为接近。
4结论
反卷积是天文图像复原的关键环节,本文采用基于伸缩梯度投影的反卷积算法实现了天文图像的高精度复原。在此基础之上,针对该算法实际应用中无法自行停止迭代的弊端,结合天文图像的特点和大量仿真,给出了一种可自行停止迭代的改进算法。仿真结果表明:改进的算法可很大程度上恢复图像的细节,能用于实际天文图像处理。
参考文献:
[1]Sheppard D G,Hunt B R,Marcellin M W.Iterative multiframe super resolution algorithms for atmospheric-turbulence-degraded imagery[J].JOSA A,1998,15(4):978-992.
[2]冈萨雷斯.数字图像处理[M].2版.阮秋琦,阮宇智,译.北京:电子工业出版社,2003.
[3]Lucy L B.An iterative technique for the rectification of observed distributions[J].The Astronomical Journal,1974,79:745.
[4]Richardson W H.Bayesian-based iterative method of image restoration[J].JOSA,1972,62(1):55-59.
[5]Bonettini S,Zanella R,Zanni L.A scaled gradient projection method for constrained image deblurring[J].Inverse Problems,2009,25(1):711-723.
[6]Zhu X,Milanfar P.Automatic parameter selection for denoising algorithms using a no-reference measure of image content[J].IEEE Transactions on Image Processing,2010,19(12):3116-3132.
[7]邵宇,孙富春,刘莹.基于局部结构张量的无参考型图像质量评价方法[J].电子与信息学报,2012,34(8):1779-1785.
[8]Zhu X,Milanfar P.QPRO:An improved no-reference image content metric using locally adapted SVD[C]∥Proceedings of Se-venth International Workshop on Video Processing and Quality Metrics for Consumer Electronics,2013.
[9]Brox T,Weickert J,Burgeth B,et al.Nonlinear structure tensor-s[J].Image and Vision Computing,2006,24(1):41-55.
[10]CoulonO,AlexanderDC,ArridgeS.Diffusiontensormagneticresonanceimageregularization[J].MedicalImageAnalysis,2004,8(1):47-67.
[11]WangZ,BovikAC,SimoncelliEP.Structuralapproachestoimagequalityassessment[J].HandbookofImageandVideoProcessing,2005,7:18.
Improvedastronomicalimagerestorationalgorithmbasedonscaledgradientprojection
LIUGuo-liang,SHAOYun-long
(SchoolofInformation&CommunicationEngineering,GuilinUniversityofElectronicTechnology,Guilin541004,China)
Abstract:In ground-based astronomy observation,overcome image blurring caused by atmosphere turbulence is key to obtain high-resolution astronomical images.Deconvolution is an important step in process of image restoration,and deconvolution algorithm based on scaled gradient projection is suitable for astronomical image restoration with high recovery precision,processing efficiency,and good robustness.But in practice,the clear images are unknown and interferences caused by noise exist,the algorithm is unable to stop iteration, making its application limited.Combined with no-reference quality measurement,an improved algorithm which can automatically stop iteration is proposed.Simulation indicates that the improved algorithm can accurately judge the optimal point and can be applied to real astronomical image processing.
Key words:ground-based astronomy; atmosphere turbulence; scaled gradient projection(SGP)
DOI:10.13873/J.1000—9787(2016)04—0134—03
收稿日期:2015—08—20
中图分类号:TP 391
文献标识码:A
文章编号:1000—9787(2016)04—0134—03
作者简介:
刘国良(1987-),男,山东临沂人,硕士研究生,主要研究方向为天文图像复原。
